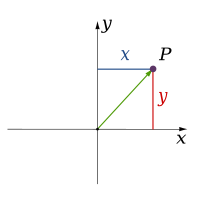Dimensão

Da esquerda para a direita: o quadrado, o cubo e o tesseract. O quadrado bidimensional (2D) é limitado por linhas unidimensionais (1D); o cubo tridimensional (3D) por áreas bidimensionais; e o tesseract (4D) tridimensional por volumes tridimensionais. Para exibição em uma superfície bidimensional, como uma tela, o cubo 3D e tesseract 4D exigem projeção.

As quatro primeiras dimensões espaciais, representadas numa imagem bidimensional.

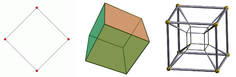
1. Dois pontos podem ser conectados para criar um segmento de linha.
2. Dois segmentos de linha paralela podem ser conectados para formar um quadrado.
3. Dois quadrados paralelos podem ser conectados para formar um cubo.
4. Dois cubos paralelos podem ser conectados para formar um tesseract.

Em física e matemática, a dimensão de um espaço matemático (ou objeto) é informalmente definida como o número mínimo de coordenadas necessárias para especificar qualquer ponto dentro dele. Assim, uma linha tem uma dimensão de um (1D) porque apenas uma coordenada é necessária para especificar um ponto nela - por exemplo, o ponto em 5 em uma linha numérica. Uma superfície, como o limite de um cilindro ou esfera, tem uma dimensão de dois (2D) porque duas coordenadas são necessárias para especificar um ponto nela - por exemplo, latitude e longitude são necessárias para localizar um ponto na superfície de uma esfera. Um espaço euclidiano bidimensional é um espaço bidimensional no plano. O interior de um cubo, um cilindro ou uma esfera é tridimensional (3D) porque são necessárias três coordenadas para localizar um ponto dentro desses espaços.

Na mecânica clássica, espaço e tempo são categorias diferentes e referem-se a espaço e tempo absolutos. Essa concepção do mundo é um espaço quadridimensional, mas não aquele que foi considerado necessário para descrever o eletromagnetismo. As quatro dimensões (4D) do espaço-tempo consistem em eventos que não são absolutamente definidos espacial e temporalmente, mas são conhecidos em relação ao movimento de um observador. O espaço de Minkowski primeiro se aproxima do universo sem gravidade; as variedades pseudo-riemannianas da relatividade geral descrevem o espaço-tempo com matéria e gravidade. 10 dimensões são usadas para descrever a teoria das supercordas (hiperespaço 6D + 4D), 11 dimensões podem descrever a supergravidade e a teoria M (hiperespaço 7D + 4D) e o estado-espaço da mecânica quântica é um espaço funcional de dimensão infinita.

O conceito de dimensão não se restringe a objetos físicos. </span Os espaços de alta dimensãos ocorrem frequentemente na matemática e nas ciências. Eles podem ser espaços euclidianos ou espaços de parâmetros mais gerais ou espaços de configuração, como na mecânica lagrangiana ou hamiltoniana; são espaços abstratos, independentes do espaço físico em que vivemos.

Em matemática

Na matemática, a dimensão de um objeto é, grosso modo, o número de graus de liberdade de um ponto que se move sobre esse objeto. Em outras palavras, a dimensão é o número de parâmetros ou coordenadas independentes necessários para definir a posição de um ponto que está restrito a estar no objeto. Por exemplo, a dimensão de um ponto é zero; a dimensão de uma linha é uma, pois um ponto pode se mover sobre uma linha em apenas uma direção (ou no sentido oposto); a dimensão de um plano é dois, etc.

A dimensão é uma propriedade intrínseca de um objeto, no sentido de que é independente da dimensão do espaço em que o objeto está ou pode estar inserido. Por exemplo, uma curva, como um círculo, tem dimensão um, porque a posição de um ponto em uma curva é determinada por sua distância sinalizada ao longo da curva até um ponto fixo na curva. Isso independe do fato de que uma curva não pode ser inserida em um espaço euclidiano de dimensão inferior a dois, a menos que seja uma linha.

A dimensão do espaço n euclidiano Eⁿ é n. Ao tentar generalizar para outros tipos de espaços, deparamo-nos com a pergunta "o que torna Eⁿ n-dimensional?" Uma resposta é que para cobrir uma bola fixa em Eⁿ por pequenas bolas de raio ε, um precisa da ordem de ε^{- n} tais bolas pequenas. Essa observação leva à definição da dimensão de Minkowski e sua variante mais sofisticada, a dimensão de Hausdorff, mas também há outras respostas para essa pergunta. Por exemplo, o limite de uma bola em Eⁿ se parece localmente com E^n-1 e isso leva à noção de dimensão indutiva. Embora essas noções concordem em Eⁿ, elas acabam sendo diferentes quando se olha em espaços mais gerais.

Um tesserato é um exemplo de objeto quadridimensional. Considerando que fora da matemática o uso do termo "dimensão" é como em: "Um tesserato tem quatro dimensões", os matemáticos geralmente expressam isso como: "O tesserato tem dimensão 4", ou: "A dimensão do tesseract é 4" ou: 4D.

Embora a noção de dimensões superiores remonte a René Descartes, o desenvolvimento substancial de uma geometria de dimensão superior só começou no século XIX, através do trabalho de Arthur Cayley, William Rowan Hamilton, Ludwig Schläfli e Bernhard Riemann. Riemann's 1854 Habilitationsschrift, Schläfli's 1852 Theorie der vielfachen Kontinuität, e a descoberta de Hamilton dos quaternions e John T. Graves's; A descoberta dos octônios em 1843 marcou o início da geometria de dimensões superiores.

O restante desta seção examina algumas das definições matemáticas mais importantes de dimensão.

Espaços vetoriais

A dimensão de um espaço vetorial é o número de vetores em qualquer base para o espaço, ou seja, o número de coordenadas necessárias para especificar qualquer vetor. Essa noção de dimensão (a cardinalidade de uma base) costuma ser chamada de dimensão de Hamel ou dimensão algébrica para distingui-la de outras noções de dimensão.

Para o caso não-livre, isso se generaliza para a noção de comprimento de um módulo.

Distribuidores

A dimensão definida exclusivamente de cada variedade topológica conectada pode ser calculada. Uma variedade topológica conectada é localmente homeomórfica ao espaço euclidiano n, no qual o número n é a dimensão do manifold.

Para variedades diferenciáveis conectadas, a dimensão também é a dimensão do espaço vetorial tangente em qualquer ponto.

Na topologia geométrica, a teoria das variedades é caracterizada pelo modo como as dimensões 1 e 2 são relativamente elementares, os casos de alta dimensão n > 4 são simplificados por ter espaço extra para "trabalhar"; e os casos n = 3 e 4 são, em alguns sentidos, os mais difíceis. Este estado de coisas foi bastante marcado nos vários casos da conjectura de Poincaré, nos quais quatro diferentes métodos de prova são aplicados.

Dimensão complexa

A dimensão de uma variedade depende do corpo base em relação ao qual o espaço euclidiano é definido. Embora a análise geralmente suponha que uma variedade esteja sobre os números reais, às vezes é útil no estudo de variedades complexas e variedades algébricas trabalhar sobre os números complexos. Um número complexo (x + iy) tem uma parte real x e uma parte imaginária y, em que x e y são ambos números reais; portanto, a dimensão complexa é metade da dimensão real.

Por outro lado, em contextos sem restrições algébricas, um único sistema de coordenadas complexo pode ser aplicado a um objeto com duas dimensões reais. Por exemplo, uma superfície esférica bidimensional comum, quando dada uma métrica complexa, torna-se uma esfera de Riemann de uma dimensão complexa.

Variedades

A dimensão de uma variedade algébrica pode ser definida de várias maneiras equivalentes. A maneira mais intuitiva é provavelmente a dimensão do espaço tangente em qualquer ponto regular de uma variedade algébrica. Outra forma intuitiva é definir a dimensão como o número de hiperplanos necessários para haver uma interseção com a variedade que se reduz a um número finito de pontos (dimensão zero). Esta definição é baseada no fato de que a interseção de uma variedade com um hiperplano reduz a dimensão em um, a menos que o hiperplano contenha a variedade.

Um conjunto algébrica sendo uma união finita de variedades algébricas, sua dimensão é o máximo das dimensões de seus componentes. É igual ao comprimento máximo das cadeias V0⊊ ⊊ V1⊊ ⊊ ⋯ ⋯ ⊊ ⊊ VDNão. V_{0}subsetneq V_{1}subsetneq cdots subsetneq V_{d}} de sub-variidades do conjunto algébrico dado (o comprimento de tal cadeia é o número de "⊊ ⊊ {displaystyle subsetneq }").

Cada variedade pode ser considerada como uma pilha algébrica, e sua dimensão como variedade coincide com sua dimensão como pilha. Existem no entanto muitas pilhas que não correspondem a variedades, algumas delas com dimensão negativa. Especificamente, se V é uma variedade de dimensão m e G é um grupo algébrico de dimensão n atuando em V, então a pilha quociente [V/G] tem dimensão m − n.

Dimensão do Krull

A dimensão de Krull de um anel comutativo é o comprimento máximo de cadeias de ideais primos nele, uma cadeia de comprimento n ser uma sequência P0⊊ ⊊ P1⊊ ⊊ ⋯ ⋯ ⊊ ⊊ Pn{displaystyle {mathcal {P}}_{0}subsetneq {mathcal {P}}_{1}subsetneq cdots subsetneq {mathcal {P}}_{n}} de ideais primos relacionados pela inclusão. É fortemente relacionado com a dimensão de uma variedade algébrica, por causa da correspondência natural entre sub-varios e ideais primos do anel dos polinômios na variedade.

Para uma álgebra sobre um corpo, a dimensão como espaço vetorial é finita se e somente se sua dimensão Krull for 0.

Espaços topológicos

Para qualquer espaço topológico normal X, a dimensão de cobertura Lebesgue de X é definido como o menor inteiro n para o qual vale o seguinte: qualquer cobertura aberta tem um refinamento aberto (uma segunda cobertura aberta na qual cada elemento é um subconjunto de um elemento na primeira capa) de modo que nenhum ponto seja incluído em mais de n + 1 elementos. Neste caso dim X = n. Para X um manifold, isso coincide com a dimensão mencionada acima. Se tal inteiro n existir, então a dimensão de X é dito ser infinito, e escreve-se dim X = ∞. Além disso, X tem dimensão −1, ou seja, dim X = −1 se e somente se X estiver vazio. Esta definição de dimensão de cobertura pode ser estendida da classe de espaços normais para todos os espaços Tychonoff simplesmente substituindo o termo "aberto" na definição pelo termo "funcionalmente aberto".

Uma dimensão indutiva pode ser definida indutivamente como segue. Considere um conjunto discreto de pontos (como uma coleção finita de pontos) como 0-dimensional. Ao arrastar um objeto 0-dimensional em alguma direção, obtém-se um objeto 1-dimensional. Ao arrastar um objeto unidimensional em uma nova direção, obtém-se um objeto bidimensional. Em geral, obtém-se um objeto dimensional (n + 1) arrastando um nobjeto dimensional em uma direção nova. A dimensão indutiva de um espaço topológico pode referir-se à pequena dimensão indutiva ou à grande dimensão indutiva, e baseia-se na analogia de que, no caso de espaços métricos, (n + 1)dimensionais as bolas têm Fronteiras ndimensionais, permitindo uma definição indutiva baseada na dimensão das fronteiras de conjuntos abertos. Além disso, o limite de um conjunto discreto de pontos é o conjunto vazio e, portanto, o conjunto vazio pode ser considerado como tendo dimensão -1.

Da mesma forma, para a classe de complexos CW, a dimensão de um objeto é o maior n para o qual o n-esqueleto não é trivial. Intuitivamente, isso pode ser descrito da seguinte forma: se o espaço original pode ser continuamente deformado em uma coleção de triângulos de dimensões superiores unidos em suas faces com uma superfície complicada, então a dimensão do objeto é a dimensão desses triângulos.

Dimensão Hausdorff

A dimensão de Hausdorff é útil para estudar conjuntos estruturalmente complicados, especialmente fractais. A dimensão de Hausdorff é definida para todos os espaços métricos e, ao contrário das dimensões consideradas acima, também pode ter valores reais não inteiros. A dimensão da caixa ou dimensão de Minkowski é uma variante da mesma ideia. Em geral, existem mais definições de dimensões fractais que funcionam para conjuntos altamente irregulares e atingem valores reais positivos não inteiros.

Espaços de Hilbert

Todo espaço de Hilbert admite uma base ortonormal, e quaisquer duas dessas bases para um espaço particular têm a mesma cardinalidade. Essa cardinalidade é chamada de dimensão do espaço de Hilbert. Essa dimensão é finita se e somente se a dimensão de Hamel do espaço for finita e, nesse caso, as duas dimensões coincidem.

Na física

Dimensões espaciais

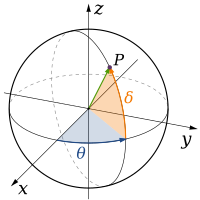
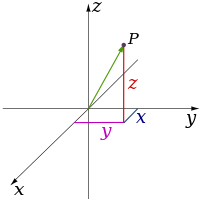
As teorias da física clássica descrevem três dimensões físicas: a partir de um determinado ponto no espaço, as direções básicas nas quais podemos nos mover são para cima/baixo, esquerda/direita e para frente/trás. O movimento em qualquer outra direção pode ser expresso em termos apenas desses três. Descer é o mesmo que subir uma distância negativa. Mover-se diagonalmente para cima e para frente é exatamente o que o nome da direção indica; isto é, movendo-se em uma combinação linear de cima e para frente. Em sua forma mais simples: uma linha descreve uma dimensão, um plano descreve duas dimensões e um cubo descreve três dimensões. (Veja Espaço e sistema de coordenadas cartesianas.)

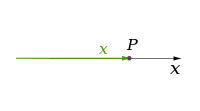
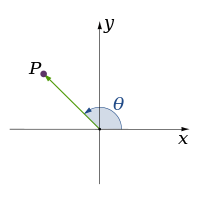
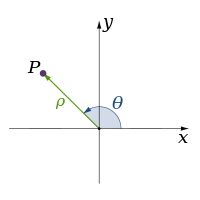
Número de dimensões	Exemplo de sistemas coordenados
1	Linha de número Ângulo
2	Cartesiano(duas dimensões) Polar Latitude e longitude
3	Cartesiano(três dimensões) Cilíndrico Esférica

Tempo

Uma dimensão temporal, ou dimensão de tempo, é uma dimensão de tempo. O tempo é muitas vezes referido como a "quarta dimensão" por esta razão, mas isso não quer dizer que seja uma dimensão espacial. Uma dimensão temporal é uma maneira de medir a mudança física. É percebido de forma diferente das três dimensões espaciais, pois existe apenas uma delas e não podemos nos mover livremente no tempo, mas nos movemos subjetivamente em uma direção.

As equações usadas na física para modelar a realidade não tratam o tempo da mesma forma que os humanos normalmente o percebem. As equações da mecânica clássica são simétricas em relação ao tempo, e as equações da mecânica quântica são tipicamente simétricas se o tempo e outras quantidades (como carga e paridade) forem invertidos. Nesses modelos, a percepção do tempo fluindo em uma direção é um artefato das leis da termodinâmica (percebemos o tempo fluindo na direção do aumento da entropia).

O tratamento mais conhecido do tempo como uma dimensão é a relatividade especial de Poincaré e Einstein (e estendida à relatividade geral), que trata o espaço e o tempo percebidos como componentes de uma variedade quadridimensional, conhecida como espaço-tempo, e no caso plano especial como espaço de Minkowski. O tempo é diferente de outras dimensões espaciais, pois o tempo opera em todas as dimensões espaciais. O tempo opera na primeira, segunda e terceira dimensões espaciais teóricas, como uma quarta dimensão espacial. No entanto, o tempo não está presente em um único ponto de singularidade infinita absoluta, conforme definido como um ponto geométrico, pois um ponto infinitamente pequeno não pode ter mudança e, portanto, nenhum tempo. Assim como quando um objeto se move por posições no espaço, ele também se move por posições no tempo. Nesse sentido, a força que move qualquer objeto para mudar é o tempo.

Dimensões adicionais

Na física, três dimensões de espaço e uma de tempo é a norma aceita. No entanto, existem teorias que tentam unificar as quatro forças fundamentais introduzindo dimensões extras/hiperespaço. Mais notavelmente, a teoria das supercordas requer 10 dimensões do espaço-tempo e se origina de uma teoria de 11 dimensões mais fundamental, provisoriamente chamada de teoria M, que engloba cinco teorias das supercordas anteriormente distintas. A teoria da supergravidade também promove espaço-tempo 11D = hiperespaço 7D + 4 dimensões comuns. Até o momento, nenhuma evidência experimental ou observacional direta está disponível para apoiar a existência dessas dimensões extras. Se o hiperespaço existe, deve estar escondido de nós por algum mecanismo físico. Uma possibilidade bem estudada é que as dimensões extras podem ser "enroladas" em escalas tão pequenas que são efetivamente invisíveis para os experimentos atuais.

Em 1921, a teoria Kaluza-Klein apresentou 5D incluindo uma dimensão extra do espaço. No nível da teoria quântica de campos, a teoria de Kaluza-Klein unifica a gravidade com interações de calibre, com base na percepção de que a gravidade se propagando em dimensões extras pequenas e compactas é equivalente a interações de calibre em longas distâncias. Em particular quando a geometria das dimensões extras é trivial, reproduz o eletromagnetismo. No entanto, em energias suficientemente altas ou em distâncias curtas, essa configuração ainda sofre das mesmas patologias que obstruem tentativas diretas de descrever a gravidade quântica. Portanto, esses modelos ainda requerem uma conclusão UV, do tipo que a teoria das cordas pretende fornecer. Em particular, a teoria das supercordas requer seis dimensões compactas (hiperespaço 6D) formando uma variedade de Calabi-Yau. Assim, a teoria de Kaluza-Klein pode ser considerada como uma descrição incompleta por conta própria ou como um subconjunto da construção do modelo da teoria das cordas.

Além de dimensões extras pequenas e enroladas, pode haver dimensões extras que não são aparentes porque a matéria associada ao nosso universo visível está localizada em um (3 + 1)-dimensional subespaço. Assim, as dimensões extras não precisam ser pequenas e compactas, mas podem ser grandes dimensões extras. D-branas são objetos estendidos dinâmicos de várias dimensionalidades previstas pela teoria das cordas que poderiam desempenhar esse papel. Eles têm a propriedade de que as excitações de cordas abertas, que estão associadas a interações de calibre, são confinadas à brana por seus pontos finais, enquanto as cordas fechadas que medeiam a interação gravitacional são livres para se propagar em todo o espaço-tempo, ou "o volume" #34;. Isso pode estar relacionado ao motivo pelo qual a gravidade é exponencialmente mais fraca do que as outras forças, pois ela efetivamente se dilui à medida que se propaga em um volume de dimensão superior.

Alguns aspectos da física das branas foram aplicados à cosmologia. Por exemplo, a cosmologia do gás brana tenta explicar por que existem três dimensões do espaço usando considerações topológicas e termodinâmicas. De acordo com essa ideia, seria porque três é o maior número de dimensões espaciais em que as cordas podem se cruzar genericamente. Se inicialmente existem muitos enrolamentos de cordas em torno de dimensões compactas, o espaço só poderia se expandir para tamanhos macroscópicos uma vez que esses enrolamentos fossem eliminados, o que requer cordas enroladas de forma oposta para se encontrarem e se aniquilarem. Mas as cordas só podem se encontrar para se aniquilar em uma taxa significativa em três dimensões, portanto, apenas três dimensões do espaço podem crescer devido a esse tipo de configuração inicial.

Dimensões extras são consideradas universais se todos os campos são igualmente livres para se propagar dentro delas.

Em computação gráfica e dados espaciais

Vários tipos de sistemas digitais são baseados no armazenamento, análise e visualização de formas geométricas, incluindo software de ilustração, desenho assistido por computador e sistemas de informação geográfica. Diferentes sistemas vetoriais usam uma ampla variedade de estruturas de dados para representar formas, mas quase todos são fundamentalmente baseados em um conjunto de primitivas geométricas correspondentes às dimensões espaciais:

• Ponto (0-dimensional), uma única coordenada num sistema de coordenadas cartesianas.
• Linha de linha ou Poliéster (1-dimensional), geralmente representado como uma lista ordenada de pontos amostrados a partir de uma linha contínua, onde o software é esperado para interpor a forma interveniente da linha como segmentos de linha reta ou curvada.
• Polígono (2-dimensional), geralmente representado como uma linha que fecha em seus pontos finais, representando o limite de uma região bidimensional. O software é esperado para usar este limite para dividir espaço 2-dimensional em um interior e exterior.
• Superfície (3-dimensional), representado usando uma variedade de estratégias, como um poliedro que consiste em rostos de polígono conectados. O software é esperado para usar esta superfície para dividir o espaço tridimensional em um interior e exterior.

Frequentemente nesses sistemas, especialmente GIS e Cartografia, uma representação de um fenômeno do mundo real pode ter uma dimensão diferente (geralmente menor) do que o fenômeno que está sendo representado. Por exemplo, uma cidade (uma região bidimensional) pode ser representada como um ponto, ou uma estrada (um volume tridimensional de material) pode ser representada como uma linha. Essa generalização dimensional se correlaciona com tendências na cognição espacial. Por exemplo, perguntar a distância entre duas cidades pressupõe um modelo conceitual das cidades como pontos, enquanto fornece direções que envolvem viagens "para cima" "para baixo" ou "junto" uma estrada implica um modelo conceitual unidimensional. Isso é frequentemente feito para fins de eficiência de dados, simplicidade visual ou eficiência cognitiva, e é aceitável se a distinção entre a representação e o representado for entendida, mas pode causar confusão se os usuários da informação assumirem que a forma digital é uma representação perfeita da realidade (ou seja, acreditar que as estradas realmente são linhas).

Na literatura

Os textos de ficção científica frequentemente mencionam o conceito de "dimensão" quando se refere a universos paralelos ou alternativos ou outros planos de existência imaginados. Esse uso é derivado da ideia de que para viajar para universos/planos de existência paralelos/alternados é preciso viajar em uma direção/dimensão além das padrão. Com efeito, os outros universos/planos estão a apenas uma pequena distância do nosso, mas a distância está em uma quarta (ou superior) dimensão espacial (ou não espacial), não as padrão.

Uma das histórias de ficção científica mais aclamadas sobre a verdadeira dimensionalidade geométrica, e frequentemente recomendada como ponto de partida para aqueles que estão começando a investigar tais assuntos, é a novela de 1884 Flatland de Edwin A. Abbott. Isaac Asimov, em seu prefácio para a edição Signet Classics 1984, descreveu Flatland como "A melhor introdução que se pode encontrar na maneira de perceber as dimensões."

A ideia de outras dimensões foi incorporada em muitas das primeiras histórias de ficção científica, aparecendo com destaque, por exemplo, em O Apêndice e os Espetáculos (1928) de Miles J. Breuer e Murray Leinster #39;s A Catapulta da Quinta Dimensão (1931); e apareceu irregularmente na ficção científica na década de 1940. Histórias clássicas envolvendo outras dimensões incluem Robert A. Heinlein's —And He Built a Crooked House (1941), em que um arquiteto da Califórnia projeta uma casa com base em uma projeção tridimensional de um tesserato; Tiger by the Tail e The Universe Between de Alan E. Nourse (ambos de 1951); e The Ifth of Oofth (1957) de Walter Tevis. Outra referência é o romance A Wrinkle In Time de Madeleine L'Engle (1962), que usa a quinta dimensão como uma forma de "tesserar o universo". ou "dobrável" espaço para atravessá-lo rapidamente. A quarta e a quinta dimensões também são um componente chave do livro O menino que se inverteu de William Sleator.

Na filosofia

Immanuel Kant, em 1783, escreveu: "Que todo o espaço (que não é em si o limite de outro espaço) tem três dimensões e que o espaço em geral não pode ter mais dimensões é baseado na proposição de que não mais do que três linhas podem se cruzar em ângulos retos em um ponto. Esta proposição não pode de forma alguma ser demonstrada a partir de conceitos, mas repousa imediatamente na intuição e, de fato, na intuição pura a priori porque é apoditicamente (demonstravelmente) certa."

"O espaço tem quatro dimensões" é um conto publicado em 1846 pelo filósofo e psicólogo experimental alemão Gustav Fechner sob o pseudônimo de "Dr. Mises'. O protagonista do conto é uma sombra consciente e capaz de se comunicar com outras sombras, mas que está presa em uma superfície bidimensional. Segundo Fechner, esse "homem-sombra" conceberia a terceira dimensão como sendo do tempo. A história tem uma forte semelhança com a "Alegoria da Caverna" apresentado em A República de Platão (c. 380 BC).

Simon Newcomb escreveu um artigo para o Bulletin of the American Mathematical Society em 1898 intitulado "The Philosophy of Hyperspace". Linda Dalrymple Henderson cunhou o termo "filosofia do hiperespaço", usado para descrever a escrita que usa dimensões superiores para explorar temas metafísicos, em sua tese de 1983 sobre a quarta dimensão na arte do início do século XX. Exemplos de "filósofos do hiperespaço" incluem Charles Howard Hinton, o primeiro escritor, em 1888, a usar a palavra "tesseract"; e o esoterista russo P. D. Ouspensky.

Mais dimensões