Difração

Um padrão de difração de um feixe de laser vermelho projetado para uma placa depois de passar por uma pequena abertura circular em outra placa

Difração é definida como a interferência ou curvatura das ondas ao redor dos cantos de um obstáculo ou através de uma abertura na região da sombra geométrica do obstáculo/abertura. O objeto de difração ou abertura torna-se efetivamente uma fonte secundária da propagação da onda. O cientista italiano Francesco Maria Grimaldi cunhou a palavra difração e foi o primeiro a registrar observações precisas do fenômeno em 1660.

Infinitamente muitos pontos (três mostrados) ao longo do comprimento D contribuições de fase de projeto da frente das ondas, produzindo uma intensidade continuamente variável θ na placa de registo.

Na física clássica, o fenômeno de difração é descrito pelo princípio de Huygens-Fresnel, que trata cada ponto em uma frente de onda de propagação como uma coleção de ondas esféricas individuais. O padrão de curvatura característico é mais pronunciado quando uma onda de uma fonte coerente (como um laser) encontra uma fenda/abertura comparável em tamanho ao seu comprimento de onda, conforme mostrado na imagem inserida. Isso se deve à adição, ou interferência, de diferentes pontos na frente de onda (ou, de forma equivalente, cada wavelet) que percorrem caminhos de diferentes comprimentos até a superfície de registro. Se houver aberturas múltiplas e estreitamente espaçadas (por exemplo, uma grade de difração), pode resultar um padrão complexo de intensidade variável.

Esses efeitos também ocorrem quando uma onda de luz viaja por um meio com um índice de refração variável ou quando uma onda sonora viaja por um meio com impedância acústica variável - todas as ondas difratam, incluindo ondas gravitacionais, ondas de água e outras ondas eletromagnéticas como raios X e ondas de rádio. Além disso, a mecânica quântica também demonstra que a matéria possui propriedades semelhantes a ondas e, portanto, sofre difração (que é mensurável em níveis subatômicos a moleculares).

A quantidade de difração depende do tamanho da lacuna. A difração é maior quando o tamanho da lacuna é semelhante ao comprimento de onda da onda. Nesse caso, quando as ondas passam pelo vão, elas se tornam semicirculares.

História

O esboço de Thomas Young de Diffraction de duas fendas para ondas de água, que ele apresentou à Royal Society em 1803.

Os efeitos da difração da luz foram cuidadosamente observados e caracterizados pela primeira vez por Francesco Maria Grimaldi, que também cunhou o termo difração, do latim diffringere, ' quebrar em pedaços', referindo-se à luz se partindo em diferentes direções. Os resultados das observações de Grimaldi foram publicados postumamente em 1665. Isaac Newton estudou esses efeitos e os atribuiu à inflexão dos raios de luz. James Gregory (1638–1675) observou os padrões de difração causados por uma pena de pássaro, que foi efetivamente a primeira rede de difração a ser descoberta. Thomas Young realizou um célebre experimento em 1803, demonstrando a interferência de duas fendas próximas umas das outras. Explicando seus resultados pela interferência das ondas que emanam das duas fendas diferentes, ele deduziu que a luz deve se propagar como ondas. Augustin-Jean Fresnel fez estudos e cálculos de difração mais definitivos, tornados públicos em 1816 e 1818, e assim deu grande apoio à teoria ondulatória da luz que havia sido avançada por Christiaan Huygens e revigorada por Young, contra a partícula de Newton. teoria.

Mecanismo

Fotografia de difração de fenda única em um tanque de ondulação circular

Na física clássica, a difração surge devido à forma como as ondas se propagam; isso é descrito pelo princípio de Huygens-Fresnel e o princípio da superposição de ondas. A propagação de uma onda pode ser visualizada considerando cada partícula do meio transmitido em uma frente de onda como uma fonte pontual para uma onda esférica secundária. O deslocamento da onda em qualquer ponto subsequente é a soma dessas ondas secundárias. Quando as ondas são somadas, sua soma é determinada pelas fases relativas, bem como pelas amplitudes das ondas individuais, de modo que a amplitude somada das ondas pode ter qualquer valor entre zero e a soma das amplitudes individuais. Portanto, os padrões de difração geralmente têm uma série de máximos e mínimos.

No entendimento da mecânica quântica moderna da propagação da luz através de uma fenda (ou fendas), todo fóton tem o que é conhecido como função de onda. A função de onda é determinada pelo ambiente físico, como geometria da fenda, distância da tela e condições iniciais quando o fóton é criado. Em experimentos importantes (um experimento de fenda dupla de baixa intensidade foi realizado pela primeira vez por G. I. Taylor em 1909, veja experimento de fenda dupla) a existência da função de onda do fóton foi demonstrada. Na abordagem quântica o padrão de difração é criado pela distribuição de probabilidade, a observação de faixas claras e escuras é a presença ou ausência de fótons nessas áreas, onde essas partículas eram mais ou menos prováveis de serem detectadas. A abordagem quântica tem algumas semelhanças notáveis com o princípio de Huygens-Fresnel; com base nesse princípio, à medida que a luz viaja através de fendas e limites, fontes de luz secundárias e pontuais são criadas próximas ou ao longo desses obstáculos, e o padrão de difração resultante será o perfil de intensidade baseado na interferência coletiva de todas essas fontes de luz que têm caminhos ópticos diferentes. Isso é semelhante a considerar as regiões limitadas ao redor das fendas e limites de onde os fótons são mais prováveis de se originarem, no formalismo quântico, e calcular a distribuição de probabilidade. Essa distribuição é diretamente proporcional à intensidade, no formalismo clássico.

Existem vários modelos analíticos que permitem o cálculo do campo difratado, incluindo a equação de difração de Kirchhoff-Fresnel que é derivada da equação de onda, a aproximação de difração de Fraunhofer da equação de Kirchhoff que se aplica ao campo distante, a difração de Fresnel aproximação que se aplica ao campo próximo e à formulação integral do caminho de Feynman. A maioria das configurações não pode ser resolvida analiticamente, mas pode produzir soluções numéricas por meio de elementos finitos e métodos de elementos de contorno.

É possível obter uma compreensão qualitativa de muitos fenômenos de difração considerando como as fases relativas das fontes de ondas secundárias individuais variam e, em particular, as condições nas quais a diferença de fase é igual a meio ciclo, caso em que as ondas se cancelam um ao outro para fora.

As descrições mais simples de difração são aquelas em que a situação pode ser reduzida a um problema bidimensional. Para ondas de água, isso já acontece; ondas de água se propagam apenas na superfície da água. Para a luz, muitas vezes podemos negligenciar uma direção se o objeto de difração se estender nessa direção por uma distância muito maior que o comprimento de onda. No caso da luz brilhando através de pequenos orifícios circulares, teremos que levar em consideração a natureza tridimensional total do problema.

• 

  Padrão de intensidade gerado por computador formado em uma tela por difração de uma abertura quadrada.

• 

  Geração de um padrão de interferência de difração de duas fendas.

• 

  Modelo computacional de um padrão de interferência de difração de duas fendas.

• 

  Padrão de difração óptica (último), (analogous to X-ray cristallography)

• 

  As cores vistas em uma teia de aranha são parcialmente devido à difração, de acordo com algumas análises.

Exemplos

Ondas circulares geradas por difração da entrada estreita de uma pedreira costeira inundada

Uma glória solar no vapor de fontes termais. Uma glória é um fenômeno ótico produzido pela luz retrocedida (uma combinação de difração, reflexão e refração) em direção à sua fonte por uma nuvem de gotículas de água de tamanho uniforme.

O ponto brilhante (ponto de Arago) visto no centro da sombra de um obstáculo circular é devido à difração

Os picos de difração são padrões de difração causados devido à abertura não circular na câmera ou suporte a struts no telescópio; Na visão normal, a difração através de pestanas pode produzir tais picos.

Espiga de difração simulada nos espelhos do telescópio hexagonal

Os efeitos da difração são frequentemente vistos na vida cotidiana. Os exemplos mais marcantes de difração são aqueles que envolvem luz; por exemplo, as faixas estreitamente espaçadas em um CD ou DVD atuam como uma grade de difração para formar o familiar padrão de arco-íris visto ao olhar para um disco. Este princípio pode ser estendido para projetar uma grade com uma estrutura tal que produzirá qualquer padrão de difração desejado; o holograma em um cartão de crédito é um exemplo. A difração na atmosfera por pequenas partículas pode fazer com que um anel brilhante seja visível em torno de uma fonte de luz brilhante como o sol ou a lua. A sombra de um objeto sólido, usando luz de uma fonte compacta, mostra pequenas franjas perto de suas bordas. O padrão speckle que é observado quando a luz do laser incide sobre uma superfície opticamente rugosa também é um fenômeno de difração. Quando a carne fria parece ser iridescente, isso é difração das fibras da carne. Todos esses efeitos são consequência do fato de que a luz se propaga como uma onda.

A difração pode ocorrer com qualquer tipo de onda. As ondas do mar se difratam em torno de molhes e outros obstáculos. As ondas sonoras podem difratar em torno de objetos, e é por isso que ainda é possível ouvir alguém chamando mesmo quando se esconde atrás de uma árvore. A difração também pode ser uma preocupação em algumas aplicações técnicas; ela estabelece um limite fundamental para a resolução de uma câmera, telescópio ou microscópio.

Outros exemplos de difração são considerados abaixo.

Difração de fenda única

difração de 2D com largura mudando animação

A aproximação numérica do padrão de difração de uma fenda de largura quatro comprimentos de onda com uma onda de avião incidente. O feixe central principal, nulas e reversões de fase são aparentes.

Gráfico e imagem de difração de fenda única.

Uma longa fenda de largura infinitesimal que é iluminada pela luz difrata a luz em uma série de ondas circulares e a frente de onda que emerge da fenda é uma onda cilíndrica de intensidade uniforme, de acordo com o princípio de Huygens-Fresnel.

Uma fenda iluminada que é mais ampla do que um comprimento de onda produz efeitos de interferência no espaço a jusante da fenda. Assumindo que a fenda se comporta como se tivesse um grande número de fontes de ponto espaçadas uniformemente através da largura dos efeitos de interferência de fenda pode ser calculado. A análise deste sistema é simplificada se considerarmos a luz de um único comprimento de onda. Se a luz incidente é coerente, todas essas fontes têm a mesma fase. O incidente de luz em um determinado ponto no espaço a jusante da fenda é composto por contribuições de cada uma dessas fontes de ponto e se as fases relativas dessas contribuições variam por 2D D - Sim. ou mais, podemos esperar encontrar minima e maxima na luz diffractada. Tais diferenças de fase são causadas por diferenças nos comprimentos do caminho sobre os quais os raios contribuintes atingem o ponto da fenda.

Podemos encontrar o ângulo em que um primeiro mínimo é obtido na luz diffratada pelo seguinte raciocínio. A luz de uma fonte localizada na borda superior da fenda interfere destrutivamente com uma fonte localizada no meio da fenda, quando a diferença de caminho entre eles é igual a λ/2. Da mesma forma, a fonte logo abaixo do topo da fenda irá interferir destrutivamente com a fonte localizada logo abaixo do meio da fenda no mesmo ângulo. Podemos continuar este raciocínio ao longo de toda a altura da fenda para concluir que a condição de interferência destrutiva para toda a fenda é a mesma que a condição de interferência destrutiva entre duas fendas estreitas uma distância à parte que é metade da largura da fenda. A diferença de caminho é aproximadamente Dpecado⁡ ⁡ (θ θ )2{displaystyle {frac {dsin(theta)}{2}}} de modo que a intensidade mínima ocorre em um ângulo θ θ mEu...n{displaystyle theta _{min}} por

Dpecado⁡ ⁡ θ θ min= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =λ λ {displaystyle d,sin theta _{text{min}}=lambda }

onde

• DNão. é a largura da fenda,
• θ θ min{displaystyle theta _{text{min}}} é o ângulo de incidência em que ocorre a intensidade mínima, e
• λ λ - Sim. é o comprimento de onda da luz

Um argumento semelhante pode ser usado para mostrar que se imaginarmos a fenda a ser dividida em quatro, seis, oito partes, etc, minima são obtidos em ângulos θ θ n{displaystyle theta _{n}} por

Dpecado⁡ ⁡ θ θ n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =nλ λ {displaystyle d,sin theta _{n}=nlambda }

onde

• nNão. é um inteiro diferente de zero.

Não existe um argumento tão simples que nos permita encontrar os máximos do padrão de difração. O perfil de intensidade pode ser calculado usando a equação de difração de Fraunhofer como

Eu...(θ θ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...0Sincronização2⁡ ⁡ (DD D λ λ pecado⁡ ⁡ θ θ ){displaystyle I(theta)=I_{0},operatorname {sinc} ^{2}left({frac {dpi }{lambda }}sin theta right)}

onde

• Eu...(θ θ ){displaystyle I(theta)} é a intensidade em um determinado ângulo,
• Eu...0Não. I_{0}} é a intensidade no máximo central (θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle theta - Sim.), que também é um fator de normalização do perfil de intensidade que pode ser determinado por uma integração de θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. D D 2{displaystyle theta - Sim. ? para θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D D 2{displaystyle theta ={frac - Sim. ? e conservação da energia.
• Sincronização⁡ ⁡ (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(pecado⁡ ⁡ xx,x≠ ≠ 01,x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle operatorname {sinc} (x)={begin{cases}{frac {sin x}{x}},&xneq 01,&x=0end{cases}}} é a função sinc não normalizada.

Essa análise se aplica apenas ao campo distante (difração de Fraunhofer), ou seja, a uma distância muito maior que a largura da fenda.

Do perfil de intensidade acima, se D≪ ≪ λ λ - Não., a intensidade terá pouca dependência θ θ - Sim., daí a orla emergente da fenda se assemelharia a uma onda cilíndrica com simetria azimutal; Se D* * λ λ - Não.Só θ θ ? ? 0{displaystyle theta approx 0 teria uma intensidade apreciável, daí a frente de onda que emerge da fenda se assemelharia à da óptica geométrica.

Quando o ângulo de incidente θ θ Eu...{displaystyle theta _{text{i}}} da luz sobre a fenda é não-zero (que causa uma mudança no comprimento do caminho), o perfil de intensidade no regime de Fraunhofer (ou seja, campo distante) torna-se:

Eu...(θ θ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...0Sincronização2⁡ ⁡ Não.DD D λ λ (pecado⁡ ⁡ θ θ ± ± pecado⁡ ⁡ θ θ Eu...)]{displaystyle I(theta)=I_{0},operatorname {sinc} ^{2}left[{frac {dpi }{lambda }}(sin theta pm sin theta _{i})right]}

A escolha do sinal plus/minus depende da definição do ângulo de incidente θ θ Eu...{displaystyle theta _{text{i}}}.

2-slit (top) e 5-slit difração de luz laser vermelho

Diffraction de um laser vermelho usando uma grade de difração.

Um padrão de difração de um laser de 633 nm através de uma grade de 150 fendas

Grade de difração

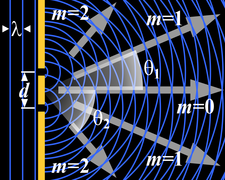
Uma grade de difração é um componente óptico com um padrão regular. A forma da luz difratada por uma grade depende da estrutura dos elementos e do número de elementos presentes, mas todas as grades têm intensidade máxima em ângulos θ_m que são dados pela equação da grade

D(pecado⁡ ⁡ θ θ m± ± pecado⁡ ⁡ θ θ Eu...)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mλ λ .{displaystyle dleft(sin {theta _{m}}pm sin {theta} _{i}}right)=mlambda.}

onde

• θ θ Eu...{displaystyle theta _{i}} é o ângulo em que a luz é incidente,
• DNão. é a separação de elementos de classificação, e
• mNão. é um inteiro que pode ser positivo ou negativo.

A luz difratada por uma grade é encontrada somando a luz difratada de cada um dos elementos e é essencialmente uma convolução de padrões de difração e interferência.

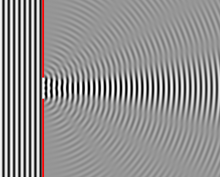
A figura mostra a luz difratada por grades de 2 e 5 elementos onde os espaçamentos das grades são iguais; pode-se ver que os máximos estão na mesma posição, mas as estruturas detalhadas das intensidades são diferentes.

Uma imagem gerada por computador de uma Disco aéreo.

Computador gerou padrão de difração de luz a partir de uma abertura circular de diâmetro 0,5 micrómetro a um comprimento de onda de 0,6 micrómetro (luz vermelha) a distâncias de 0,1 cm – 1 cm em passos de 0,1 cm. Pode-se ver a imagem movendo-se da região de Fresnel para a região de Fraunhofer onde o padrão Airy é visto.

Abertura circular

A difração de campo distante de uma onda plana incidente em uma abertura circular é frequentemente chamada de disco aéreo. A variação da intensidade com o ângulo é dada por

Eu...(θ θ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...0(2JJ1(kumpecado⁡ ⁡ θ θ )kumpecado⁡ ⁡ θ θ )2{displaystyle I(theta)=I_{0}left({frac {2J_{1}(kasin theta)}{kasin theta }}right)^{2}},

onde a é o raio da abertura circular, k é igual a 2π/λ e J₁ é uma função de Bessel. Quanto menor a abertura, maior o tamanho do ponto a uma determinada distância e maior a divergência dos feixes difratados.

Abertura geral

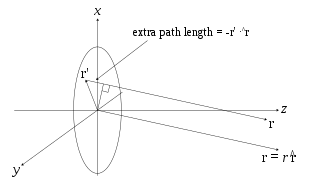
A onda que emerge de uma fonte de ponto tem amplitude ? ? - Sim. na localização r que é dada pela solução da equação de onda de domínio de frequência para uma fonte de ponto (a equação de Helmholtz),

? ? 2? ? +k2? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ (R){displaystyle nabla ^{2}psi +k^{2}psi =delta (mathbf {r})}

Onde? δ δ (R){displaystyle delta (mathbf {r})} é a função delta tridimensional. A função delta tem apenas dependência radial, então o operador Laplace (a.k.a. scalar Laplacian) no sistema de coordenadas esféricas simplifica para (veja del em coordenadas cilíndricas e esféricas)

? ? 2? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1R∂ ∂ 2∂ ∂ R2(R? ? ){displaystyle nabla ^{2}psi ={frac {1}{r}}{frac {partial ^{2}}{partial r^{2}}}(rpsi)}

Por substituição direta, a solução para esta equação pode ser facilmente mostrada para ser a função de Green escalar, que no sistema de coordenadas esféricas (e usando a convenção do tempo de física e- Sim. - Sim. Eu...ω ω ){displaystyle e^{-iomega t)) é:

? ? (R)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =eEu...kR4D D R{displaystyle psi (r)={frac (e^{ikr){4pi)

Esta solução assume que a fonte de função delta está localizada na origem. Se a fonte está localizada em um ponto de origem arbitrário, denotado pelo vetor R?Não. e o ponto de campo está localizado no ponto R- Sim., então podemos representar a função do verde escalar (para localização de fonte arbitrária) como:

? ? (R|R?)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =eEu...k|R- Sim. - Sim. R?|4D D |R- Sim. - Sim. R?|(mathbf {r} |mathbf {r})={frac {e^{ik|mathbf {r} |mathbf {r} |mathbf {r} |mathbf {r})={frac {e^{ik|mathbf {r} - Sim. '|}}{4pi |mathbf {r} - Sim. '|}}}

Portanto, se um campo elétrico, E_inc(x,y) incide na abertura, o campo produzido por esta abertura distribuição é dada pela integral de superfície:

Telecomunicações Telecomunicações (R)∝ ∝ ∫ ∫ ∫ ∫ umpeR)uReEEu...nc(x?,Sim.?)eEu...k|R- Sim. - Sim. R?|4D D |R- Sim. - Sim. R?|Dx?DSim.?,{displaystyle Psi (r)propto iint limits _{mathrm {aperture} }E_{mathrm {inc} }(x',y')~{frac {e^{ik|mathbf {r} - Sim. '|}}{4pi |mathbf {r} -mathbf {r} '|}},dx',dy',}

No cálculo dos campos da região de Fraunhofer

onde o ponto de origem na abertura é dado pelo vetor

R?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x?x^ ^ +Sim.?Sim.^ ^ {displaystyle mathbf {r}=x'mathbf {hat {x}}} - Sim.

No campo distante, onde a aproximação de raios paralelos pode ser empregada, a função de Green,

? ? (R|R?)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =eEu...k|R- Sim. - Sim. R?|4D D |R- Sim. - Sim. R?|(mathbf {r} |mathbf {r})={frac {e^{ik|mathbf {r} |mathbf {r} |mathbf {r} |mathbf {r})={frac {e^{ik|mathbf {r} - Sim. '|}}{4pi |mathbf {r} - Sim. '|}}}

simplifica para

? ? (R|R?)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =eEu...kR4D D Re- Sim. - Sim. Eu...k(R?)) R^ ^ ){displaystyle psi (mathbf {r} |mathbf {r})={frac {e^{ikr}}{4pi r}}e^{-ik(mathbf {r}cdot mathbf {hat {r}}}}}}}}}}}}

como pode ser visto na figura ao lado (clique para ampliar).

A expressão para o campo de zona distante (região de Fraunhofer) torna-se

Telecomunicações Telecomunicações (R)∝ ∝ eEu...kR4D D R∫ ∫ ∫ ∫ umpeR)uReEEu...nc(x?,Sim.?)e- Sim. - Sim. Eu...k(R?)) R^ ^ )Dx?DSim.?,(r)propto {frac {e^{ikr}}{4pi r}}iint limits _{mathrm {aperture} }E_{mathrm {inc} }(x',y')e^{-ik(mathbf {r}cdot mathbf {hat {r}})},dx}','

Agora, desde

R?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x?x^ ^ +Sim.?Sim.^ ^ {displaystyle mathbf {r}=x'mathbf {hat {x}}} - Sim.

e

R^ ^ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =pecado⁡ ⁡ θ θ e⁡ ⁡ φ φ x^ ^ +pecado⁡ ⁡ θ θ pecado⁡ ⁡ φ φ Sim.^ ^ +e⁡ ⁡ θ θ zangão.^ ^ {displaystyle mathbf {hat {r}}} =sin theta cos phi mathbf {hat {x}} +sin theta ~sin phi ~mathbf {hat {y}} +cos theta mathbf {hat {z}} }

a expressão para o campo da região de Fraunhofer de uma abertura planar agora se torna,

Telecomunicações Telecomunicações (R)∝ ∝ eEu...kR4D D R∫ ∫ ∫ ∫ umpeR)uReEEu...nc(x?,Sim.?)e- Sim. - Sim. Eu...kpecado⁡ ⁡ θ θ (e⁡ ⁡ φ φ x?+pecado⁡ ⁡ φ φ Sim.?)Dx?DSim.?{displaystyle Psi (r)propto {frac {e^{ikr}}{4pi r}}iint limits _{mathrm {aperture} }E_{mathrm {inc} }(x',y')e^{-iksin theta (cos phi x'+sin phi y')},dx',dy'}

Deixar,

kx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =kpecado⁡ ⁡ θ θ e⁡ ⁡ φ φ {displaystyle k_{x}=ksin theta cos phi ,!}

e

kSim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =kpecado⁡ ⁡ θ θ pecado⁡ ⁡ φ φ Não. k_{y}=ksin theta sin phi ,!}

o campo da região de Fraunhofer da abertura planar assume a forma de uma transformada de Fourier

Telecomunicações Telecomunicações (R)∝ ∝ eEu...kR4D D R∫ ∫ ∫ ∫ umpeR)uReEEu...nc(x?,Sim.?)e- Sim. - Sim. Eu...(kxx?+kSim.Sim.?)Dx?DSim.?,{displaystyle Psi (r)propto {frac {e^{ikr}}{4pi r}}iint limits _{mathrm {aperture} }E_{mathrm {inc} }(x',y')e^{-i(k_{x}x'+k_{y}y')},dx',dy',}

Na região de campo distante / Fraunhofer, isso se torna a transformada espacial de Fourier da distribuição de abertura. Huygens' princípio quando aplicado a uma abertura simplesmente diz que o padrão de difração de campo distante é a transformada espacial de Fourier da forma da abertura, e este é um subproduto direto do uso da aproximação de raios paralelos, que é idêntico a fazer uma decomposição de onda plana dos campos do plano de abertura (ver óptica de Fourier).

Propagação de um feixe de laser

A maneira como o perfil do feixe de um feixe de laser muda à medida que se propaga é determinada pela difração. Quando todo o feixe emitido tem uma frente de onda plana e espacialmente coerente, ele se aproxima do perfil gaussiano do feixe e tem a menor divergência para um determinado diâmetro. Quanto menor o feixe de saída, mais rápido ele diverge. É possível reduzir a divergência de um feixe de laser expandindo-o primeiro com uma lente convexa e depois colimando-o com uma segunda lente convexa cujo ponto focal coincide com o da primeira lente. O feixe resultante tem um diâmetro maior e, portanto, uma menor divergência. A divergência de um feixe de laser pode ser reduzida abaixo da difração de um feixe gaussiano ou mesmo revertida para convergência se o índice de refração do meio de propagação aumentar com a intensidade da luz. Isso pode resultar em um efeito de autofoco.

Quando a frente de onda do feixe emitido tem perturbações, apenas o comprimento de coerência transversal (onde a perturbação da frente de onda é menor que 1/4 do comprimento de onda) deve ser considerado como diâmetro gaussiano do feixe ao determinar a divergência do laser feixe. Se o comprimento de coerência transversal na direção vertical for maior do que na horizontal, a divergência do feixe de laser será menor na direção vertical do que na horizontal.

Imagem limitada por difração

O disco Airy em torno de cada uma das estrelas da abertura do telescópio de 2,56 m pode ser visto neste imagem de sorte da estrela binária zeta Boötis.

A capacidade de um sistema de imagem para resolver detalhes é limitada pela difração. Isso ocorre porque uma onda plana incidente em uma lente circular ou espelho é difratada conforme descrito acima. A luz não é focada em um ponto, mas forma um disco de Airy com um ponto central no plano focal cujo raio (medido para o primeiro nulo) é

? ? x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1.22λ λ NNão. Delta x=1.22lambda Não.

onde λ é o comprimento de onda da luz e N é o número f (comprimento focal f dividido pelo diâmetro de abertura D) da óptica de imagem; isso é estritamente preciso para N≫1 (caso paraxial). No espaço do objeto, a resolução angular correspondente é

θ θ ? ? pecado⁡ ⁡ θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1.22λ λ D,{displaystyle theta approx sin theta =1.22{frac {lambda }{D}},,}

onde D é o diâmetro da pupila de entrada da lente de imagem (por exemplo, do espelho principal de um telescópio).

Duas fontes pontuais produzirão cada uma um padrão Airy – veja a foto de uma estrela binária. À medida que as fontes pontuais se aproximam, os padrões começarão a se sobrepor e, por fim, se fundirão para formar um único padrão; nesse caso, as duas fontes pontuais não poderão ser resolvidas na imagem. O critério de Rayleigh especifica que duas fontes pontuais são consideradas "resolvidas" se a separação das duas imagens for pelo menos o raio do disco de Airy, ou seja, se o primeiro mínimo de uma coincidir com o máximo da outra.

Assim, quanto maior a abertura da lente em comparação com o comprimento de onda, melhor a resolução de um sistema de imagem. Esta é uma das razões pelas quais os telescópios astronômicos requerem grandes objetivas e porque as objetivas do microscópio requerem uma grande abertura numérica (grande diâmetro de abertura em comparação com a distância de trabalho) para obter a maior resolução possível.

Padrões de manchas

O padrão de speckle visto ao usar um apontador laser é outro fenômeno de difração. É o resultado da superposição de muitas ondas com diferentes fases, que são produzidas quando um feixe de laser ilumina uma superfície rugosa. Eles se somam para dar uma onda resultante cuja amplitude e, portanto, intensidade, varia aleatoriamente.

Princípio de Babinet

O princípio de Babinet é um teorema útil que afirma que o padrão de difração de um corpo opaco é idêntico ao de um orifício do mesmo tamanho e forma, mas com intensidades diferentes. Isso significa que as condições de interferência de uma única obstrução seriam as mesmas de uma única fenda.

"Borda da navalha"

O efeito faca ou difração faca é um truncamento de uma parte da radiação incidente que atinge um obstáculo bem definido, como uma montanha alcance ou a parede de um edifício. O efeito de ponta de faca é explicado pelo princípio de Huygens-Fresnel, que afirma que uma obstrução bem definida a uma onda eletromagnética atua como uma fonte secundária e cria uma nova frente de onda. Esta nova frente de onda se propaga na área de sombra geométrica do obstáculo.

A difração em ponta de faca é uma consequência do "problema do meio plano", originalmente resolvido por Arnold Sommerfeld usando uma formulação de espectro de onda plana. Uma generalização do problema do meio plano é o "problema da cunha", solucionável como um problema de valor de contorno em coordenadas cilíndricas. A solução em coordenadas cilíndricas foi então estendida para o regime óptico por Joseph B. Keller, que introduziu a noção de coeficientes de difração por meio de sua teoria geométrica da difração (GTD). Pathak e Kouyoumjian estenderam os coeficientes (singulares) de Keller através da teoria uniforme da difração (UTD).

• 

  Diffraction em uma borda metálica afiada

• 

  Diffraction em uma abertura suave, com um gradiente de condutividade sobre a largura da imagem

Padrões

A metade superior desta imagem mostra um padrão de difração do feixe de laser He-Ne em uma abertura elíptica. A metade inferior é a sua transformação 2D Fourier aproximadamente reconstruindo a forma da abertura.

Várias observações qualitativas podem ser feitas de difração em geral:

• O espaçamento angular das características no padrão de difração é inversamente proporcional às dimensões do objeto causando a difração. Em outras palavras: Quanto menor o objeto diffracting, o 'wider' o padrão de difração resultante, e vice-versa. (Mais precisamente, isso é verdade dos pecados dos ângulos.)
• Os ângulos de difração são invariantes sob escala; isto é, eles dependem apenas da relação do comprimento de onda ao tamanho do objeto difração.
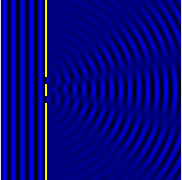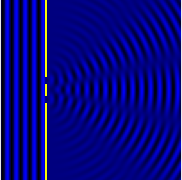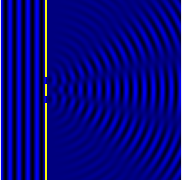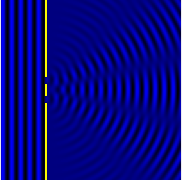
• Quando o objeto difração tem uma estrutura periódica, por exemplo, em uma grade de difração, as características geralmente se tornam mais nítidas. A terceira figura, por exemplo, mostra uma comparação de um padrão de dupla fenda com um padrão formado por cinco fendas, ambos os conjuntos de fendas com o mesmo espaçamento, entre o centro de uma fenda e o próximo.

Difração de partículas

De acordo com a teoria quântica, toda partícula exibe propriedades ondulatórias. Em particular, partículas massivas podem interferir consigo mesmas e, portanto, difratar. A difração de elétrons e nêutrons permaneceu como um dos poderosos argumentos a favor da mecânica quântica. O comprimento de onda associado a uma partícula é o comprimento de onda de Broglie

λ λ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =hp{displaystyle lambda ={frac Não.

onde h é a constante de Planck e p é o momento da partícula (massa × velocidade para partículas em movimento lento).

Para a maioria dos objetos macroscópicos, esse comprimento de onda é tão curto que não faz sentido atribuir um comprimento de onda a eles. Um átomo de sódio viajando a cerca de 30.000 m/s teria um comprimento de onda De Broglie de cerca de 50 picometros.

Como o comprimento de onda até mesmo para o menor dos objetos macroscópicos é extremamente pequeno, a difração de ondas de matéria é visível apenas para pequenas partículas, como elétrons, nêutrons, átomos e pequenas moléculas. O comprimento de onda curto dessas ondas de matéria as torna ideais para estudar a estrutura cristalina atômica de sólidos e grandes moléculas como proteínas.

Moléculas relativamente maiores, como buckyballs, também mostraram difratar.

Difração de Bragg

Seguindo a lei de Bragg, cada ponto (ou reflexão) neste padrão de difração forma a partir da interferência construtiva de raios-X passando por um cristal. Os dados podem ser usados para determinar a estrutura atômica do cristal.

A difração de uma estrutura periódica tridimensional, como átomos em um cristal, é chamada de difração de Bragg. É semelhante ao que ocorre quando as ondas são espalhadas por uma grade de difração. A difração de Bragg é uma consequência da interferência entre ondas refletidas em diferentes planos cristalinos. A condição de interferência construtiva é dada pela Lei de Bragg:

mλ λ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2Dpecado⁡ ⁡ θ θ {displaystyle mlambda =2dsin theta ?

onde

• λ é o comprimento de onda,
• D é a distância entre os planos de cristal,
• θ é o ângulo da onda difração.
• e m é um inteiro conhecido como o ordem do feixe difração.

A difração de Bragg pode ser realizada usando radiação eletromagnética de comprimento de onda muito curto, como raios X, ou ondas de matéria, como nêutrons (e elétrons), cujo comprimento de onda é da ordem de (ou muito menor que) o espaçamento atômico. O padrão produzido dá informação das separações dos planos cristalográficos d, permitindo deduzir a estrutura cristalina. O contraste de difração, em microscópios eletrônicos e dispositivos de topografia x em particular, também é uma ferramenta poderosa para examinar defeitos individuais e campos de deformação locais em cristais.

Coerência

A descrição da difração baseia-se na interferência de ondas que emanam da mesma fonte tomando diferentes caminhos para o mesmo ponto em uma tela. Nesta descrição, a diferença de fase entre as ondas que seguiram caminhos diferentes depende apenas do comprimento efetivo do caminho. Isso não leva em consideração o fato de que as ondas que chegam na tela ao mesmo tempo foram emitidas pela fonte em momentos diferentes. A fase inicial com que a fonte emite ondas pode mudar ao longo do tempo de forma imprevisível. Isso significa que as ondas emitidas pela fonte em tempos muito distantes não podem mais formar um padrão de interferência constante, pois a relação entre suas fases não é mais independente do tempo.

O comprimento ao longo do qual a fase em um feixe de luz é correlacionada é chamado de comprimento de coerência. Para que a interferência ocorra, a diferença do comprimento do caminho deve ser menor que o comprimento de coerência. Isso às vezes é chamado de coerência espectral, pois está relacionado à presença de diferentes componentes de frequência na onda. No caso da luz emitida por uma transição atômica, o comprimento de coerência está relacionado ao tempo de vida do estado excitado a partir do qual o átomo fez sua transição.

Se as ondas forem emitidas de uma fonte estendida, isso pode levar à incoerência na direção transversal. Ao olhar para uma seção transversal de um feixe de luz, o comprimento ao longo do qual a fase está correlacionada é chamado de comprimento de coerência transversal. No caso do experimento de fenda dupla de Young, isso significaria que, se o comprimento de coerência transversal for menor que o espaçamento entre as duas fendas, o padrão resultante em uma tela pareceria com dois padrões de difração de fenda única.

No caso de partículas como elétrons, nêutrons e átomos, o comprimento de coerência está relacionado à extensão espacial da função de onda que descreve a partícula.

Aplicativos

Difração antes da destruição

Uma nova maneira de visualizar partículas biológicas individuais surgiu desde a década de 2010, utilizando os raios-X brilhantes gerados por lasers de elétrons livres de raios-X. Esses pulsos de duração de femtosegundo permitirão a imagem (potencial) de macromoléculas biológicas únicas. Devido a esses pulsos curtos, os danos da radiação podem ser superados e os padrões de difração de macromoléculas biológicas individuais poderão ser obtidos.