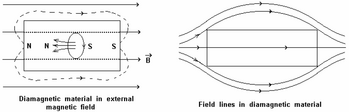
Diamagnetismo
diamagnéticos são repelidos por um campo magnético; um campo magnético aplicado cria um campo magnético induzido neles na direção oposta, causando uma força repulsiva. Em contraste, materiais paramagnéticos e ferromagnéticos são atraídos por um campo magnético. O diamagnetismo é um efeito da mecânica quântica que ocorre em todos os materiais; quando é a única contribuição para o magnetismo, o material é chamado de diamagnético. Em substâncias paramagnéticas e ferromagnéticas, a força diamagnética fraca é superada pela força atrativa dos dipolos magnéticos no material. A permeabilidade magnética dos materiais diamagnéticos é menor que a permeabilidade do vácuo, μ0. Na maioria dos materiais, o diamagnetismo é um efeito fraco que pode ser detectado apenas por instrumentos de laboratório sensíveis, mas um supercondutor age como um forte diamagnetismo porque repele um campo magnético inteiramente de seu interior.
O diamagnetismo foi descoberto pela primeira vez quando Anton Brugmans observou em 1778 que o bismuto era repelido por campos magnéticos. Em 1845, Michael Faraday demonstrou que era uma propriedade da matéria e concluiu que todo material respondia (de maneira diamagnética ou paramagnética) a um campo magnético aplicado. Por sugestão de William Whewell, Faraday primeiro se referiu ao fenômeno como diamagnético (o prefixo dia- significando através de ou através i>), depois mudou para diamagnetismo.
Uma regra prática simples é usada em química para determinar se uma partícula (átomo, íon ou molécula) é paramagnética ou diamagnética: Se todos os elétrons na partícula estiverem emparelhados, então a substância feita dessa partícula é diamagnética; Se tiver elétrons desemparelhados, a substância é paramagnética.
Materiais
| Material | χm 10.-5 (unidades SI)] |
|---|---|
| Supercondutor | - Sim.5 |
| Carbono pirolítico | -40.9 |
| Bismuto | -16% |
| Neon. | -6.74 |
| Mercúrio | -2.9 |
| Prata | -2.6 |
| Carbono (diamond) | -1 |
| Liderança | -1,8 |
| Carbono (grafita) | - 1.6. |
| Cobre | -1.0 |
| Água | -0.91 |
O diamagnetismo é uma propriedade de todos os materiais e sempre dá uma contribuição fraca para a resposta do material a um campo magnético. No entanto, outras formas de magnetismo (como ferromagnetismo ou paramagnetismo) são muito mais fortes que, quando várias formas diferentes de magnetismo estão presentes em um material, a contribuição diamagnética é geralmente insignificante. As substâncias em que o comportamento diamagnético é o efeito mais forte são denominadas materiais diamagnéticos ou diamagnetos. Materiais diamagnéticos são aqueles que algumas pessoas geralmente consideram não magnéticos e incluem água, madeira, a maioria dos compostos orgânicos, como petróleo e alguns plásticos, e muitos metais, incluindo cobre, particularmente os pesados com muitos elétrons do núcleo, como mercúrio, ouro e bismuto. Os valores de suscetibilidade magnética de vários fragmentos moleculares são chamados de constantes de Pascal.
Materiais diamagnéticos, como água ou materiais à base de água, têm uma permeabilidade magnética relativa menor ou igual a 1 e, portanto, uma suscetibilidade magnética menor ou igual a 0, pois a suscetibilidade é definida como χv = μv − 1. Isso significa que materiais diamagnéticos são repelidos por campos magnéticos. No entanto, como o diamagnetismo é uma propriedade tão fraca, seus efeitos não são observáveis na vida cotidiana. Por exemplo, a suscetibilidade magnética de diamagnetos como a água é χv = −9.05×10−6 . O material diamagnético mais forte é o bismuto, χv = −1,66×10−4 , embora o carbono pirolítico possa ter uma suscetibilidade de χv = −4.00×10−4 em um plano. No entanto, esses valores são ordens de grandeza menores do que o magnetismo exibido por paramagnetos e ferromagnetos. Como χv é derivado da razão entre o campo magnético interno e o campo aplicado, é um valor adimensional.
Em casos raros, a contribuição diamagnética pode ser mais forte que a contribuição paramagnética. Este é o caso do ouro, que tem uma suscetibilidade magnética inferior a 0 (e é, portanto, por definição, um material diamagnético), mas quando medido cuidadosamente com dicroísmo circular magnético de raios-X, tem uma contribuição paramagnética extremamente fraca que é superada por uma forte contribuição diamagnética.
Supercondutores
Os supercondutores podem ser considerados diamagnetos perfeitos (χv = −1), porque eles expulsam todos os campos magnéticos (exceto em uma camada superficial fina) devido ao efeito Meissner.
Demonstrações
Curvando superfícies de água
Se um ímã poderoso (como um superímã) for coberto por uma camada de água (que é fina em comparação com o diâmetro do ímã), o campo do ímã repele significativamente a água. Isso causa uma leve ondulação na superfície da água que pode ser vista por um reflexo em sua superfície.
Levitação
Os diamagnetos podem ser levitados em equilíbrio estável em um campo magnético, sem consumo de energia. O teorema de Earnshaw parece excluir a possibilidade de levitação magnética estática. No entanto, o teorema de Earnshaw se aplica apenas a objetos com suscetibilidades positivas, como ferromagnetos (que têm um momento positivo permanente) e paramagnetos (que induzem um momento positivo). Estes são atraídos por máximos de campo, que não existem no espaço livre. Os diamagnetos (que induzem um momento negativo) são atraídos por mínimos de campo e pode haver um mínimo de campo no espaço livre.
Uma fina fatia de grafite pirolítica, que é um material fortemente diamagnético incomum, pode flutuar de forma estável em um campo magnético, como o de ímãs permanentes de terras raras. Isso pode ser feito com todos os componentes à temperatura ambiente, tornando uma demonstração visualmente eficaz e relativamente conveniente do diamagnetismo.
A Radboud University Nijmegen, na Holanda, conduziu experimentos onde água e outras substâncias foram levitadas com sucesso. Mais espetacularmente, um sapo vivo (veja a figura) foi levitado.
Em setembro de 2009, o Laboratório de Propulsão a Jato (JPL) da NASA em Pasadena, Califórnia, anunciou que conseguiu levitar camundongos usando um ímã supercondutor, um importante passo à frente, já que os camundongos são biologicamente mais próximos dos humanos do que os sapos. O JPL disse que espera realizar experimentos sobre os efeitos da microgravidade na massa óssea e muscular.
Experiências recentes que estudam o crescimento de cristais de proteína levaram a uma técnica que usa ímãs poderosos para permitir o crescimento de maneiras que neutralizam a gravidade da Terra.
Um simples dispositivo caseiro para demonstração pode ser construído a partir de placas de bismuto e alguns ímãs permanentes que levitam um ímã permanente.
Teoria
Os elétrons em um material geralmente se acomodam em orbitais, com resistência efetivamente zero e agem como loops de corrente. Assim, pode-se imaginar que efeitos de diamagnetismo em geral seriam comuns, pois qualquer campo magnético aplicado geraria correntes nesses loops que se oporiam à mudança, de forma semelhante aos supercondutores, que são diamagnetos essencialmente perfeitos. No entanto, uma vez que os elétrons são mantidos rigidamente em orbitais pela carga dos prótons e são ainda mais limitados pelo princípio de exclusão de Pauli, muitos materiais exibem diamagnetismo, mas normalmente respondem muito pouco ao campo aplicado.
O teorema de Bohr–Van Leeuwen prova que não pode haver qualquer diamagnetismo ou paramagnetismo em um sistema puramente clássico. No entanto, a teoria clássica de Langevin para o diamagnetismo dá a mesma previsão que a teoria quântica. A teoria clássica é dada abaixo.
Diamagnetismo de Langevin
A teoria do diamagnetismo de Paul Langevin (1905) aplica-se a materiais contendo átomos com invólucros fechados (ver dielétricos). Um campo com intensidade B, aplicado a um elétron com carga e e massa m, dá origem à precessão de Larmor com frequência ω = eB / 2m. O número de revoluções por unidade de tempo é ω / 2π , então a corrente para um átomo com Z elétrons é (em unidades SI)
- Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. Z.e2B4D D m.Não. Eu... {Ze^{2}B}{4pi Sim.
O momento magnético de um laço atual é igual aos tempos atuais a área do laço. Suponha que o campo esteja alinhado com o zangão. eixo. A área de loop média pode ser dada como D D ⟨? ? 2){displaystyle scriptstyle pi leftlangle rho ^{2}rightrangle }, onde ⟨? ? 2){displaystyle scriptstyle leftlangle rho ^{2}rightrangle } é a distância quadrada média dos elétrons perpendicular ao zangão. eixo. O momento magnético é, portanto,
- μ μ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. Z.e2B4m⟨ ⟨ ? ? 2)) .{displaystyle mu =-{frac {Ze^{2}B}{4m}}langle rho ^{2}rangle.}
Se a distribuição de carga é esféricamente simétrica, podemos supor que a distribuição de X,y,z coordenadas são independentes e distribuídas de forma idêntica. Então... ⟨x2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨Sim.2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨zangão.2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =13⟨R2){displaystyle scriptstyle leftlangle x^{2}rightrangle ;=;leftlangle y^{2}rightrangle ;=;leftlangle z^{2}rightrangle ;=;{frac {1}{3}}leftlangle r^{2}rightrangle }, onde ⟨R2){displaystyle scriptstyle leftlangle r^{2}rightrangle } é a distância quadrada média dos elétrons do núcleo. Portanto, ⟨? ? 2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨x2)+⟨Sim.2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =23⟨R2){displaystyle scriptstyle leftlangle rho ^{2}rightrangle ;=;leftlangle x^{2}rightrangle ;+;leftlangle y^{2}rightrangle ;=;{frac {2}{3}}leftlangle r^{2}rightrangle }. Se nNão. é o número de átomos por volume unitário, a susceptibilidade diamagnética de volume em unidades SI é
- χ χ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ 0nμ μ B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. μ μ 0e2Z.n6m⟨ ⟨ R2)) .{displaystyle chi ={frac - Sim. }{B}}=-{frac Sim. _{0}e^{2}Zn}{6m}}langle r^{2}rangle.}
Nos átomos, a suscetibilidade de Langevin é da mesma ordem de grandeza que a suscetibilidade paramagnética de Van Vleck.
Em metais
A teoria de Langevin não é o quadro completo para os metais porque também existem elétrons não localizados. A teoria que descreve o diamagnetismo em um gás de elétrons livres é chamada de diamagnetismo de Landau, em homenagem a Lev Landau, e, em vez disso, considera o fraco campo contrário que se forma quando os elétrons se movem. trajetórias são curvas devido à força de Lorentz. O diamagnetismo de Landau, no entanto, deve ser contrastado com o paramagnetismo de Pauli, um efeito associado à polarização de elétrons deslocalizados' rotaciona. Para o caso a granel de um sistema 3D e campos magnéticos baixos, a suscetibilidade diamagnética (volume) pode ser calculada usando a quantização de Landau, que em unidades SI é
- χ χ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. μ μ 0e212D D 2m? ? 2mEF,Não. chi =-mu _{0} {e^{2}}{12pi ^{2}mhbar {sqrt {2mE_{rm {F}}}
Onde? EFO que é isso? (F) é a energia Fermi. Isto é equivalente a - Sim. - Sim. μ μ 0μ μ B2g(EF)/3Não. -mu _{0}mu _{rm {B}}^{2}g(E_{rm {F}}/3}Exatamente. - Sim. - Sim. 1/3- Sim. tempos Pauli susceptibilidade paramagnética, onde μ μ B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e? ? /2m{displaystyle mu _{rm {B}}=ehbar /2m} é o magneton Bohr e g(E)(E)} é a densidade de estados (número de estados por energia por volume). Esta fórmula leva em conta a degeneração do spin dos portadores (pin 1⁄2 elétrons).
Em semicondutores dopados, a razão entre as suscetibilidades de Landau e Pauli pode mudar devido à massa efetiva dos portadores de carga diferir da massa do elétron no vácuo, aumentando a contribuição diamagnética. A fórmula aqui apresentada aplica-se apenas ao bulk; em sistemas confinados como pontos quânticos, a descrição é alterada devido ao confinamento quântico. Além disso, para campos magnéticos fortes, a suscetibilidade de elétrons deslocalizados oscila em função da intensidade do campo, um fenômeno conhecido como efeito De Haas–Van Alphen, também descrito teoricamente pela primeira vez por Landau.
Contenido relacionado
Eletricidade
Eletromagnetismo
Hipótese da censura cósmica