Diagrama de Feynman
Na física teórica, um diagrama de Feynman é uma representação pictórica das expressões matemáticas que descrevem o comportamento e a interação das partículas subatômicas. O esquema recebeu o nome do físico americano Richard Feynman, que introduziu os diagramas em 1948. A interação de partículas subatômicas pode ser complexa e difícil de entender; Os diagramas de Feynman fornecem uma visualização simples do que, de outra forma, seria uma fórmula misteriosa e abstrata. De acordo com David Kaiser, "Desde meados do século 20, os físicos teóricos têm se voltado cada vez mais para esta ferramenta para ajudá-los a realizar cálculos críticos. Os diagramas de Feynman revolucionaram quase todos os aspectos da física teórica." Embora os diagramas sejam aplicados principalmente à teoria quântica de campos, eles também podem ser usados em outras áreas da física, como a teoria do estado sólido. Frank Wilczek escreveu que os cálculos que lhe renderam o Prêmio Nobel de Física de 2004 "seriam literalmente impensáveis sem os diagramas de Feynman, assim como os cálculos [de Wilczek] que estabeleceram uma rota para a produção e observação da partícula de Higgs."
Feynman usou a interpretação de Ernst Stueckelberg do pósitron como se fosse um elétron se movendo para trás no tempo. Assim, as antipartículas são representadas como movendo-se para trás ao longo do eixo do tempo nos diagramas de Feynman.
O cálculo das amplitudes de probabilidade na física de partículas teórica requer o uso de integrais bastante grandes e complicadas sobre um grande número de variáveis. Os diagramas de Feynman podem representar essas integrais graficamente.
Um diagrama de Feynman é uma representação gráfica de uma contribuição perturbativa para a amplitude de transição ou função de correlação de uma mecânica quântica ou teoria de campo estatística. Dentro da formulação canônica da teoria quântica de campos, um diagrama de Feynman representa um termo na expansão de Wick da matriz S perturbativa. Alternativamente, a formulação do caminho integral da teoria quântica de campos representa a amplitude de transição como uma soma ponderada de todas as histórias possíveis do sistema desde o estado inicial até o estado final, em termos de partículas ou campos. A amplitude de transição é então dada como o elemento de matriz da matriz S entre os estados inicial e final do sistema quântico.
Motivação e história
Ao calcular as seções transversais de espalhamento na física de partículas, a interação entre as partículas pode ser descrita começando de um campo livre que descreve as partículas de entrada e saída e incluindo uma interação hamiltoniana para descrever como as partículas desviam umas das outras. A amplitude do espalhamento é a soma de cada história de interação possível sobre todos os possíveis estados intermediários de partícula. O número de vezes que a interação hamiltoniana atua é a ordem da expansão da perturbação, e a teoria da perturbação dependente do tempo para campos é conhecida como série de Dyson. Quando os estados intermediários em tempos intermediários são auto-estados de energia (coleções de partículas com um momento definido), a série é chamada de teoria de perturbação antiquada (ou teoria de perturbação dependente do tempo/ordenada no tempo).
A série de Dyson pode ser alternativamente reescrita como uma soma sobre os diagramas de Feynman, onde em cada vértice tanto a energia quanto o momento são conservados, mas onde o comprimento do quadrivetor energia-momento não é necessariamente igual à massa, ou seja, as partículas intermediárias são as chamadas off-shell. Os diagramas de Feynman são muito mais fáceis de acompanhar do que os diagramas "antiquados" termos, porque a maneira antiga trata as contribuições de partícula e antipartícula como separadas. Cada diagrama de Feynman é a soma exponencial de muitos termos antiquados, porque cada linha interna pode representar separadamente uma partícula ou uma antipartícula. Em uma teoria não relativística, não há antipartículas e não há duplicação, então cada diagrama de Feynman inclui apenas um termo.
Feynman forneceu uma receita para calcular a amplitude (as regras de Feynman, abaixo) para qualquer diagrama a partir de uma teoria de campo Lagrangeana. Cada linha interna corresponde a um fator do propagador da partícula virtual; cada vértice onde as linhas se encontram fornece um fator derivado de um termo de interação no Lagrangiano, e as linhas que entram e saem carregam energia, momento e rotação.
Além de seu valor como ferramenta matemática, os diagramas de Feynman fornecem informações físicas profundas sobre a natureza das interações de partículas. As partículas interagem de todas as formas disponíveis; na verdade, as partículas virtuais intermediárias podem se propagar mais rápido que a luz. A probabilidade de cada estado final é então obtida pela soma de todas essas possibilidades. Isso está intimamente ligado à formulação integral funcional da mecânica quântica, também inventada por Feynman - veja formulação integral de caminho.
A aplicação ingênua de tais cálculos geralmente produz diagramas cujas amplitudes são infinitas, porque as interações de partículas de curta distância requerem um procedimento de limitação cuidadoso, para incluir as auto-interações de partículas. A técnica de renormalização, sugerida por Ernst Stueckelberg e Hans Bethe e implementada por Dyson, Feynman, Schwinger e Tomonaga compensa esse efeito e elimina os problemáticos infinitos. Após a renormalização, os cálculos usando diagramas de Feynman correspondem aos resultados experimentais com precisão muito alta.
Os métodos de diagrama de Feynman e integral de caminho também são usados em mecânica estatística e podem até ser aplicados à mecânica clássica.
Nomes alternativos
Murray Gell-Mann sempre se referiu aos diagramas de Feynman como diagramas de Stueckelberg, em homenagem ao físico suíço Ernst Stueckelberg, que desenvolveu uma notação semelhante muitos anos antes. Stueckelberg foi motivado pela necessidade de um formalismo manifestamente covariante para a teoria quântica de campos, mas não forneceu uma maneira automatizada de lidar com fatores de simetria e loops, embora tenha sido o primeiro a encontrar a interpretação física correta em termos de avanço e retrocesso no tempo. caminhos, todos sem a integral do caminho.
Historicamente, como um dispositivo de contabilidade da teoria de perturbação covariante, os gráficos eram chamados de diagramas de Feynman-Dyson ou gráficos de Dyson, porque a integral de caminho não era familiar quando eles foram introduzidas, e a derivação de Freeman Dyson da antiquada teoria de perturbação emprestada das expansões perturbativas em mecânica estatística foi mais fácil de seguir para físicos treinados em métodos anteriores. Feynman teve que fazer um forte lobby pelos diagramas, o que confundiu os físicos tradicionais treinados em equações e gráficos.
Representação da realidade física
Em suas apresentações de interações fundamentais, escritas a partir da perspectiva da física de partículas, Gerard 't Hooft e Martinus Veltman apresentaram bons argumentos para considerar os diagramas de Feynman originais e não regularizados como a representação mais sucinta de nosso conhecimento atual sobre a física da dispersão quântica de partículas fundamentais. Suas motivações são consistentes com as convicções de James Daniel Bjorken e Sidney Drell:
Os gráficos de Feynman e as regras de cálculo resumem a teoria quântica de campo em uma forma em contato próximo com os números experimentais que se quer entender. Embora a afirmação da teoria em termos de gráficos possa implicar a teoria da perturbação, o uso de métodos gráficos no problema de muitos corpos mostra que este formalismo é flexível o suficiente para lidar com fenômenos de caracteres não perturbativos... Algumas modificações das regras de cálculo de Feynman podem bem superar a elaborada estrutura matemática da teoria do campo quântico canônico local...
Atualmente, não há opiniões contrárias. Nas teorias quânticas de campos, os diagramas de Feynman são obtidos de um Lagrangiano pelas regras de Feynman.
A regularização dimensional é um método para regularizar integrais na avaliação de diagramas de Feynman; atribui-lhes valores que são funções meromorfas de um parâmetro complexo auxiliar d, chamado de dimensão. A regularização dimensional escreve uma integral de Feynman como uma integral dependendo da dimensão do espaço-tempo d e dos pontos do espaço-tempo.
Interpretação do caminho de partícula
Um diagrama de Feynman é uma representação dos processos da teoria quântica de campos em termos de interações de partículas. As partículas são representadas pelas linhas do diagrama, que podem ser onduladas ou retas, com ou sem seta, dependendo do tipo de partícula. Um ponto onde as linhas se conectam a outras linhas é um vértice, e é aqui que as partículas se encontram e interagem: emitindo ou absorvendo novas partículas, desviando umas das outras ou mudando de tipo.
Existem três tipos diferentes de linhas: linhas internas conectam dois vértices, linhas de entrada se estendem do "passado" para um vértice e representam um estado inicial, e as linhas de saída se estendem de um vértice para "o futuro" e representam o estado final (os dois últimos também são conhecidos como linhas externas). Tradicionalmente, a parte inferior do diagrama é o passado e a parte superior o futuro; outras vezes, o passado está à esquerda e o futuro à direita. Ao calcular funções de correlação em vez de amplitudes de dispersão, não há passado e futuro e todas as linhas são internas. As partículas então começam e terminam em pequenos x's, que representam as posições dos operadores cuja correlação está sendo calculada.
Os diagramas de Feynman são uma representação pictórica de uma contribuição para a amplitude total de um processo que pode acontecer de várias maneiras diferentes. Quando um grupo de partículas recebidas deve se espalhar, o processo pode ser pensado como aquele em que as partículas viajam por todos os caminhos possíveis, incluindo caminhos que retrocedem no tempo.
Os diagramas de Feynman são frequentemente confundidos com diagramas de espaço-tempo e imagens de câmara de bolhas porque todos descrevem a dispersão de partículas. Diagramas de Feynman são gráficos que representam a interação de partículas em vez da posição física da partícula durante um processo de espalhamento. Ao contrário de uma imagem de câmara de bolhas, apenas a soma de todos os diagramas de Feynman representa qualquer interação de partícula; as partículas não escolhem um diagrama específico cada vez que interagem. A lei da soma está de acordo com o princípio da superposição – cada diagrama contribui para a amplitude total do processo.
Descrição
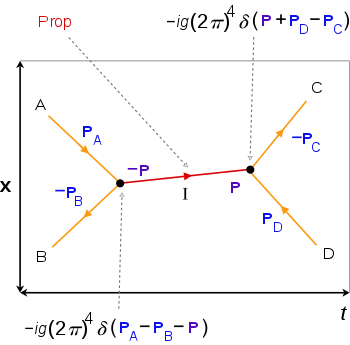
• linhas internas (vermelho) para partículas e processos intermediários, que tem um fator propagador ("prop"), linhas externas (laranja) para as partículas de entrada / saída a / de vértices (preto),
• em cada vértice há conservação 4-momento usando funções delta, 4-momenta entrando no vértice são positivos enquanto aqueles que deixam são negativos, os fatores em cada vértice e linha interna são multiplicados na integral da amplitude,
• espaço x e tempo ) os eixos nem sempre são mostrados, as direções de linhas externas correspondem à passagem do tempo.
Um diagrama de Feynman representa uma contribuição perturbativa para a amplitude de uma transição quântica de algum estado quântico inicial para algum estado quântico final.
Por exemplo, no processo de aniquilação elétron-pósitron, o estado inicial é um elétron e um pósitron, o estado final: dois fótons.
O estado inicial é geralmente considerado à esquerda do diagrama e o estado final à direita (embora outras convenções também sejam usadas com bastante frequência).
Um diagrama de Feynman consiste em pontos, chamados vértices, e linhas conectadas aos vértices.
As partículas no estado inicial são representadas por linhas saindo na direção do estado inicial (por exemplo, para a esquerda), as partículas no estado final são representadas por linhas saindo na direção do estado final (ex., para a direita).
Na QED existem dois tipos de partículas: partículas de matéria, como elétrons ou pósitrons (chamadas férmions) e partículas de troca (chamadas bósons de calibre). Eles são representados nos diagramas de Feynman da seguinte forma:
- O elétron no estado inicial é representado por uma linha sólida, com uma seta que indica o giro da partícula, por exemplo, apontando para o vértice (→•).
- Eletron no estado final é representado por uma linha, com uma seta que indica o giro da partícula, por exemplo, apontando para longe do vértice: (•→).
- Positron no estado inicial é representado por uma linha sólida, com uma flecha indicando o giro da partícula, por exemplo, apontando para longe do vértice: (••).
- Positron no estado final é representado por uma linha, com uma seta que indica o giro da partícula, por exemplo, apontando para o vértice: (•).
- Virtual Photon na inicial e o estado final é representado por uma linha de ondulação (~ e - Sim.).
No QED, um vértice sempre tem três linhas anexadas a ele: uma linha bosônica, uma linha fermiônica com seta em direção ao vértice e uma linha fermiônica com seta afastada do vértice.
Os vértices podem ser conectados por um propagador bosônico ou fermiônico. Um propagador bosônico é representado por uma linha ondulada conectando dois vértices (•~•). Um propagador fermiônico é representado por uma linha sólida (com uma seta em uma ou outra direção) conectando dois vértices, (•←•).
O número de vértices dá a ordem do termo na expansão da série de perturbação da amplitude de transição.
Exemplo de aniquilação elétron-pósitron
A interação de aniquilação elétron-pósitron:
- e+ + e- Sim. → 2 γ
tem uma contribuição do diagrama de Feynman de segunda ordem mostrado ao lado:
No estado inicial (no fundo; tempo inicial) há um elétron (e−) e um pósitron (e+) e no estado final (no topo; hora tardia) há dois fótons (γ).
Formulação de quantização canônica
A amplitude de probabilidade para uma transição de um sistema quântico (entre estados assintoticamente livres) do estado inicial |i⟩ para o estado final | f ⟩ é dado pelo elemento da matriz
- SfEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨ ⟨ f|S|Eu...)) ,Não. S_{rm {fi}}=langle mathrm {f} |S|mathrm {i} rangle ;,}
onde S é a matriz S. Em termos do operador de evolução temporal U, é simplesmente
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Limpar.)2→ → +∞ ∞ Limpar.)1→ → - Sim. - Sim. ∞ ∞ U()2,)1).Não. S = _{t_{2}rightarrow +infty }lim _{t_{1}rightarrow -infty }U(t_{2},t_{1});.}
Na imagem de interação, isso se expande para
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Te- Sim. - Sim. Eu...∫ ∫ - Sim. - Sim. ∞ ∞ +∞ ∞ D? ? H. H. H.V(? ? ).Não. S. {T}}e^{-iint _{-infty }^{+infty }dtau H_{V}(tau)}.}
onde HV é o hamiltoniano de interação e o estilo T significa o produto ordenado por tempo dos operadores. A fórmula de Dyson expande a matriz ordenada no tempo exponencial em uma série de perturbações nas potências da interação densidade hamiltoniana,
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0∞ ∞ (- Sim. - Sim. Eu...)nn!(? ? JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n∫ ∫ D4xJJ)T(? ? JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nH. H. H.V(xJJ)?)) Gerenciamento Gerenciamento n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0∞ ∞ S(n).{displaystyle S=sum _{n=0}^{infty }{frac {(-i)^{n}}{n!}}left(prod) _{j=1}^{n}int d^{4}x_{j}right){mathcal {T}}left{prod _{j=1}^{n}{mathcal {H}}_{V}left(x_{j}right)right}equiv sum _{n=0}^{infty }S^{(n)};.}
Equivalentemente, com a interação Lagrangeana LV, é
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0∞ ∞ Eu...nn!(? ? JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n∫ ∫ D4xJJ)T(? ? JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nLV(xJJ)?)) Gerenciamento Gerenciamento n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0∞ ∞ S(n).- Sim. _{n=0}^{infty }{frac {i^{n}}{n!}}left(prod _{j=1}^{n}int d^{4}x_{j}right){mathcal {T}}left{prod _{j=1}^{n}{mathcal {L}}_{V}left(x_{j}right)right}equiv sum _{n=0}^{infty }S^{(n)};.}
Um diagrama de Feynman é uma representação gráfica de um único summand na expansão de Wick do produto ordenado no tempo no n termo de terceira ordem S(n) da série Dyson de a matriz S,
- T? ? JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nLV(xJJ)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento A(± ± )N? ? JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nLV(xJJ),{displaystyle {mathcal {T}}prod _{j=1}^{n}{mathcal {L}}_{V}left(x_{j}right)=sum _{text{A}}(pm){mathcal {N}}prod _{j=1}^{n}{mathcal {L}}_{V}left(x_{j}right);,}
onde N significa o produto ordenado normal dos operadores e (±) cuida da possível mudança de sinal ao comutar os operadores fermiônicos para reuni-los para uma contração (um propagador) e A representa todas as contrações possíveis.
Regras de Feynman
Os diagramas são desenhados de acordo com as regras de Feynman, que dependem da interação Lagrangeana. Para a interação QED Lagrangeana
- Lv= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. g? ? ? ? γ γ μ μ ? ? Aμ μ Não. L_{v}=-g{bar {psi }}gamma ^{mu }psi A_{mu }}
descrevendo a interação de um campo fermiônico ψ com um campo bosônico Aμ, as regras de Feynman podem ser formuladas no espaço de coordenadas da seguinte forma:
- Cada coordenação de integração xJJ é representado por um ponto (às vezes chamado de vértice);
- Um propagador bosônico é representado por uma linha wiggly conectando dois pontos;
- Um propagador fermiônico é representado por uma linha sólida conectando dois pontos;
- Um campo bosônico Aμ μ (xEu...)(x_{i})} é representado por uma linha wiggly anexada ao ponto xEu...;
- Um campo fermiônico ?(xEu...) é representado por uma linha sólida anexada ao ponto xEu... com uma seta para o ponto;
- Um campo anti-fermiônico ?(xEu...) é representado por uma linha sólida anexada ao ponto xEu... com uma seta longe do ponto;
Exemplo: processos de segunda ordem em QED
O termo de perturbação de segunda ordem na matriz S é
- S(2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(Eu...e)22!∫ ∫ D4xD4x?T? ? ? ? (x)γ γ μ μ ? ? (x)Aμ μ (x)? ? ? ? (x?)γ γ Processo Processo ? ? (x?)AProcesso Processo (x?).{displaystyle S^{(2)}={frac {(ie)^{2}}{2!}}int d^{4}x,d^{4}x',T{bar {psi }}(x),gamma ^{mu },psi (x),A_{mu }(x),{bar {psi }}(x'),gamma ^{nu'
Dispersão de férmions
A expansão de Wick do integrando dá (entre outros) o seguinte termo
- N? ? ? ? (x)γ γ μ μ ? ? (x)? ? ? ? (x?)γ γ Processo Processo ? ? (x?)Aμ μ (x)AProcesso Processo (x?)Não. Não. ,{displaystyle N{bar {psi }}(x)gamma ^{mu }psi (x){bar {psi }}(x')gamma ^{nu }psi (x'){underline {A_{mu }(x)A_{nu }(x')}};}
onde
- Aμ μ (x)AProcesso Processo (x?)Não. Não. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ D4k(2D D )4- Sim. - Sim. Eu...gμ μ Processo Processo k2+Eu...0e- Sim. - Sim. Eu...k(x- Sim. - Sim. x?)Não. (A_{mu }(x)A_{nu }(x')}}=int {frac {d^{4}k}{(2pi)^{4}}}{frac {-ig_{mu nu }}{k^{2}+i0}}e^{-ik(x-x')}}
é a contração eletromagnética (propagador) no medidor de Feynman. Este termo é representado pelo diagrama de Feynman à direita. Este diagrama dá contribuições para os seguintes processos:
- e- Sim. e- Sim. dispersão (estado inicial à direita, estado final à esquerda do diagrama);
- e+ e+ dispersão (estado inicial à esquerda, estado final à direita do diagrama);
- e- Sim. e+ dispersão (estado inicial na parte inferior / superior, estado final na parte superior / inferior do diagrama).
Dispersão Compton e aniquilação/geração de pares e− e+
Outro termo interessante na expansão é
- N? ? ? ? (x)γ γ μ μ ? ? (x)? ? ? ? (x?)Não. Não. γ γ Processo Processo ? ? (x?)Aμ μ (x)AProcesso Processo (x?),Não. N{bar {psi }}(x),gamma ^{mu },{underline {psi (x),{bar {psi }}(x')}},gamma ^{nu },psi (x'),A_{mu }(x),A_{nu }(x');,}
onde
- ? ? (x)? ? ? ? (x?)Não. Não. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ D4p(2D D )4Eu...γ γ p- Sim. - Sim. m+Eu...0e- Sim. - Sim. Eu...p(x- Sim. - Sim. x?){displaystyle {underline {psi (x){bar {psi }}(x')}}=int {frac {d^{4}p}{(2pi)^{4}}}{frac {i}{gamma p-m+i0}}e^{-ip(x-x')}}
é a contração fermiônica (propagador).
Formulação de integral de caminho
Em uma integral de caminho, o Lagrangeano de campo, integrado sobre todas as histórias de campo possíveis, define a amplitude de probabilidade para ir de uma configuração de campo para outra. Para fazer sentido, a teoria de campo deve ter um estado fundamental bem definido, e a integral deve ser executada um pouco rotacionada no tempo imaginário, ou seja, uma rotação de Wick. O formalismo de integral de caminho é completamente equivalente ao formalismo de operador canônico acima.
Lagrangeano de campo escalar
Um exemplo simples é o campo escalar relativístico livre em dimensões d, cuja integral de ação é:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 12∂ ∂ μ μ φ φ ∂ ∂ μ μ φ φ DDx.{displaystyle S=int {tfrac {1}{2}}partial _{mu }phi partial ^{mu }phi ,d^{d}x,.}
A amplitude de probabilidade para um processo é:
- ∫ ∫ ABeEu...SDφ φ ,{displaystyle int _{A}^{B}e^{iS},Dphi ,}
onde A e B são hipersuperfícies espaciais que definem as condições de contorno. A coleção de todos os φ(A) na hipersuperfície inicial fornece o valor inicial do campo, análogo ao posição inicial para uma partícula pontual e os valores de campo φ(B) em cada ponto da hipersuperfície final definem a valor final do campo, que pode variar, dando uma amplitude diferente para terminar em valores diferentes. Esta é a amplitude de transição campo a campo.
A integral do caminho fornece o valor esperado dos operadores entre o estado inicial e final:
- ∫ ∫ ABeEu...Sφ φ (x1)⋯ ⋯ φ φ (xn)Dφ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨A|φ φ (x1)⋯ ⋯ φ φ (xn)|B),{displaystyle int _{A}^{B}e^{iS}phi (x_{1})cdots phi (x_{n}),Dphi =leftlangle Aleft|phi (x_{1})cdots phi (x_{n})right| Brightrangle ,}
e no limite em que A e B recuam para o passado infinito e o futuro infinito, a única contribuição que importa é do estado fundamental (isso só é rigorosamente verdadeiro se a integral do caminho for definida ligeiramente rotacionada no tempo imaginário). A integral de caminho pode ser considerada análoga a uma distribuição de probabilidade e é conveniente defini-la de forma que a multiplicação por uma constante não altere nada:
- ∫ ∫ eEu...Sφ φ (x1)⋯ ⋯ φ φ (xn)Dφ φ ∫ ∫ eEu...SDφ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨0|φ φ (x1)⋯ ⋯ φ φ (xn)|0).{displaystyle {frac {displaystyle int e^{iS}phi (x_{1})cdots phi (x_{n}),Dphi }{displaystyle int e^{iS},Dphi }}=leftlangle 0left|phi (x_{1})cdots phi (x_{n})right|0rightrangle,
O fator de normalização na parte inferior é chamado de função de partição para o campo e coincide com a função de partição mecânica estatística na temperatura zero quando girado em tempo imaginário.
As amplitudes inicial a final são mal definidas se pensarmos no limite contínuo desde o início, porque as flutuações no campo podem se tornar ilimitadas. Portanto, a integral de caminho pode ser considerada como uma rede quadrada discreta, com espaçamento de rede a e o limite a → 0 deve ser tomado com cuidado. Se os resultados finais não dependerem da forma da rede ou do valor de a, então o limite contínuo existe.
Em uma treliça
Em uma rede, (i), o campo pode ser expandido em modos de Fourier:
- φ φ (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ Dk(2D D )Dφ φ (k)eEu...k)) x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ kφ φ (k)eEu...kx.{displaystyle phi (x)=int {frac {dk}{(2pi)^{d}}}phi (k)e^{ikcdot x}=int _{k}phi (k)e^{ikx},.}
Aqui o domínio de integração é k restrito a um cubo de comprimento lateral 2π/a, para que valores grandes de k não sejam permitido. É importante observar que a medida k contém os fatores de 2π das transformadas de Fourier, esta é a melhor convenção padrão para k-integrais em QFT. A rede significa que as flutuações em grande k não podem contribuir imediatamente, elas só começam a contribuir no limite a → 0. Às vezes, em vez de uma rede, os modos de campo são apenas cortados em valores altos de k.
Também é conveniente, de tempos em tempos, considerar o volume do espaço-tempo como finito, de modo que os modos k também são uma treliça. Isso não é tão necessário quanto o limite de rede espacial, porque as interações em k não são localizadas, mas é conveniente para manter rastreie os fatores na frente das k-integrais e as funções delta de conservação de momento que surgirão.
Em uma rede, (ii), a ação precisa ser discretizada:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento ⟨ ⟨ x,Sim.)) 12(φ φ (x)- Sim. - Sim. φ φ (Sim.))2,Não. S=sum _{langle x,yrangle }{tfrac {1}{2}}{big (}phi (x)-phi (y){big)}^{2},}
onde ⟨x,y⟩ é um par dos vizinhos de rede mais próximos x e y. A discretização deve ser pensada como definindo o que a derivada ∂μφ significa.
Em termos dos modos de Fourier da rede, a ação pode ser escrita:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ k((1- Sim. - Sim. e (k1))+(1- Sim. - Sim. e (k2))+⋯ ⋯ +(1- Sim. - Sim. e (kD)))φ φ k∗ ∗ φ φ k.Não. S. _{k}{Big (}{big (}1-cos(k_{1}){big (}1-cos(k_{2}){big)}+cdots +{big (}1-cos(k_{d}){big)}{Big)}phi _{k}^{*phi ^{k},}
Para k próximo de zero, isto é:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ k12k2|φ φ (k)|2.Não. S=int _{k}{tfrac {1}{2}}k^{2}left|phi (k)right|^{2},.}
Agora temos a transformada de Fourier contínua da ação original. Em volume finito, a quantidade ddk não é infinitesimal, mas torna-se o volume de uma caixa feita por modos vizinhos de Fourier, ou (2π/V)d
.
O campo φ tem valor real, então a transformada de Fourier obedece:
- φ φ (k)∗ ∗ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ (- Sim. - Sim. k).{displaystyle phi (k)^{*}=phi (-k),.}
Em termos de partes reais e imaginárias, a parte real de φ(k) é uma função par de k, enquanto a parte imaginária é ímpar. A transformada de Fourier evita a contagem dupla, de modo que pode ser escrita:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ k12k2φ φ (k)φ φ (- Sim. - Sim. k)Não. S=int _{k}{tfrac {1}{2}}k^{2}phi (k)phi (-k)}
sobre um domínio de integração que integra sobre cada par (k,−k) exatamente uma vez.
Para um campo escalar complexo com ação
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 12∂ ∂ μ μ φ φ ∗ ∗ ∂ ∂ μ μ φ φ DDx{displaystyle S=int {tfrac {1}{2}}partial _{mu }phi ^{*}partial ^{mu }phi ,d^{d}x}
a transformada de Fourier é irrestrita:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ k12k2|φ φ (k)|2Não. S=int _{k}{tfrac {1}{2}}k^{2}left|phi (k)right|^{2}}
e a integral é sobre tudo k.
Integrar sobre todos os diferentes valores de φ(x) é equivalente a integrar sobre todos os modos de Fourier, porque tomar uma transformada de Fourier é uma transformação linear unitária de coordenadas de campo. Quando você altera as coordenadas em uma integral multidimensional por uma transformação linear, o valor da nova integral é dado pelo determinante da matriz de transformação. Se
- Sim.Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =AEu...JJxJJ,Não. y_{i}=A_{ij}x_{j},}
então
- - Não.(A)∫ ∫ Dx1Dx2⋯ ⋯ Dxn= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ DSim.1DSim.2⋯ ⋯ DSim.n.{displaystyle det(A)int dx_{1},dx_{2}cdots ,dx_{n}=int dy_{1},dy_{2}cdots ,dy_{n},.}
Se A é uma rotação, então
- ATA= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...Não. A^{mathrm {T} }A=I}
de modo que det A = ±1, e o sinal depende se a rotação inclui uma reflexão ou não.
A matriz que altera as coordenadas de φ(x) para φ(k) pode ser lido a partir da definição de uma transformada de Fourier.
- Akx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =eEu...kxNão. A_{kx}=e^{ikx},}
e o teorema da inversão de Fourier informa o inverso:
- Akx- Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e- Sim. - Sim. Eu...kxNão. A_{kx}^{-1}=e^{-ikx},}
que é a transposição conjugada complexa, até fatores de 2π. Em uma rede de volume finito, o determinante é diferente de zero e independente dos valores do campo.
- - Não.A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1{displaystyle det A=1,}
e a integral do caminho é um fator separado em cada valor de k.
- ∫ ∫ exp (Eu...2Gerenciamento Gerenciamento kk2φ φ ∗ ∗ (k)φ φ (k))Dφ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? k∫ ∫ φ φ keEu...2k2|φ φ k|2DDk{displaystyle int exp left({frac - Não. _{k}k^{2}phi ^{*}(k)phi (k)right),Dphi =prod _{k}int _{phi _{k}}e^{{frac {i}{2}}k^{2}left|phi _{k}right|^{2},d^{d}k},}
O fator ddk é o volume infinitesimal de uma célula discreta em k-espaço, em uma caixa de treliça quadrada
- DDk= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(1L)D,Não. d^{d}k=left({frac {1}{L}}right)^{d},}
onde L é o comprimento lateral da caixa. Cada fator separado é um Gaussiano oscilatório, e a largura do Gaussiano diverge à medida que o volume vai para o infinito.
No tempo imaginário, a ação euclidiana torna-se positiva definida e pode ser interpretada como uma distribuição de probabilidade. A probabilidade de um campo ter valores φk é
- e∫ ∫ k- Sim. - Sim. 12k2φ φ k∗ ∗ φ φ k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? ke- Sim. - Sim. k2|φ φ k|2DDk.{displaystyle e^{int _{k}-{tfrac {1}{2}}k^{2}phi _{k}^{*}phi _{k}}=prod _{k}e^{-k^{2}left|phi _{k}right|^{2},d^{d}k},.}
O valor esperado do campo é o valor esperado estatístico do campo quando escolhido de acordo com a distribuição de probabilidade:
- ⟨φ φ (x1)⋯ ⋯ φ φ (xn))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ e- Sim. - Sim. Sφ φ (x1)⋯ ⋯ φ φ (xn)Dφ φ ∫ ∫ e- Sim. - Sim. SDφ φ {displaystyle leftlangle phi (x_{1})cdots phi (x_{n})rightrangle ={frac {displaystyle int e^{-S}phi (x_{1})cdots phi (x_{n}),Dphi }{displaystyle int e^{-S},Dphi }}}}}}
Como a probabilidade de φk é um produto, o valor de φk em cada valor separado de k é uma distribuição gaussiana independente. A variação do gaussiano é 1/k2ddk, que é formalmente infinito, mas isso significa apenas que as flutuações são ilimitadas em volume infinito. Em qualquer volume finito, a integral é substituída por uma soma discreta e a variância da integral é V/k2.
Monte Carlo
A integral de caminho define um algoritmo probabilístico para gerar uma configuração de campo escalar euclidiano. Escolha aleatoriamente as partes reais e imaginárias de cada modo de Fourier no número de onda k para ser uma variável aleatória gaussiana com variação 1/k2. Isso gera uma configuração φC(k) aleatoriamente, e a transformada de Fourier fornece φC(x). Para campos escalares reais, o algoritmo deve gerar apenas um de cada par φ(k), φ(−k), e torne o segundo o conjugado complexo do primeiro.
Para encontrar qualquer função de correlação, gere um campo repetidas vezes por este procedimento e encontre a média estatística:
- ⟨φ φ (x1)⋯ ⋯ φ φ (xn))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Limpar.|C|→ → ∞ ∞ Gerenciamento Gerenciamento Cφ φ C(x1)⋯ ⋯ φ φ C(xn)|C|{displaystyle leftlangle phi (x_{1})cdots phi (x_{n})rightrangle =lim _{|C|rightarrow infty }{frac {displaystyle sum _{C}phi _{C}(x_{1})cdots phi _{C}(x_{n})}{|C|}}})}
onde |C| é o número de configurações e a soma é o produto dos valores dos campos em cada configuração. A função de correlação euclidiana é exatamente igual à função de correlação em estatística ou mecânica estatística. As funções de correlação da mecânica quântica são uma continuação analítica das funções de correlação euclidianas.
Para campos livres com uma ação quadrática, a distribuição de probabilidade é uma gaussiana de alta dimensão e a média estatística é dada por uma fórmula explícita. Mas o método de Monte Carlo também funciona bem para teorias de campo de interação bosônica, onde não há forma fechada para as funções de correlação.
Propagador escalar
Cada modo é Gaussiano distribuído independentemente. A expectativa dos modos de campo é fácil de calcular:
- ⟨φ φ kφ φ k?)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle leftlangle phi _{k}phi _{k'}rightrangle =0,}
para k ≠ k′, desde então as duas variáveis aleatórias gaussianas são independentes e ambas têm média zero.
- ⟨φ φ kφ φ k)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Vk2{displaystyle leftlangle phi _{k}phi _{k}rightrangle ={frac {V}{k^{2}}
em volume finito V, quando os dois k-valores coincidem, pois esta é a variância do gaussiano. No limite de volume infinito,
- ⟨φ φ (k)φ φ (k?))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ (k- Sim. - Sim. k?)1k2{displaystyle leftlangle phi (k)phi (k')rightrangle =delta (k-k'){frac {1}{k^{2}}
Estritamente falando, isso é uma aproximação: o propagador da rede é:
- ⟨φ φ (k)φ φ (k?))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ (k- Sim. - Sim. k?)12(D- Sim. - Sim. e (k1)+e (k2)⋯ ⋯ +e (kD)){displaystyle leftlangle phi (k)phi (k')rightrangle =delta (k-k'){frac {1}{2{big (}d-cos(k_{1})+cos(k_{2})cdots +cos(k_{d}){big)}}}}}}}}
Mas perto de k = 0, para flutuações de campo longas comparadas ao espaçamento da rede, as duas formas coincidem.
É importante ressaltar que as funções delta contêm fatores de 2π, de forma que cancelam o 2π fatores na medida para k integrais.
- δ δ (k)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(2D D )Dδ δ D(k1)δ δ D(k2)⋯ ⋯ δ δ D(kD){displaystyle delta (k)=(2pi)^{d}delta _{D}(k_{1})delta _{D}(k_{2})cdots delta _{D}(k_{d}),}
onde δD(k) é o delta de Dirac unidimensional comum função. Esta convenção para funções delta não é universal—alguns autores mantêm os fatores de 2π nas funções delta (e no k-integration) explícito.
Equação de movimento
A forma do propagador pode ser encontrada mais facilmente usando a equação de movimento para o campo. Do Lagrangeano, a equação do movimento é:
- ∂ ∂ μ μ ∂ ∂ μ μ φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle partial _{mu }partial ^{mu }phi =0,}
e em um valor esperado, isso diz:
- ∂ ∂ μ μ ∂ ∂ μ μ ⟨φ φ (x)φ φ (Sim.))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle partial _{mu }partial ^{mu }leftlangle phi (x)phi (y)rightrangle =0}
Onde as derivadas atuam em x e a identidade é verdadeira em todos os lugares, exceto quando x e y coincidem e a ordem do operador é importante. A forma da singularidade pode ser entendida a partir das relações de comutação canônica como sendo uma função delta. Definindo o (euclidiano) propagador de Feynman Δ como a transformada de Fourier da função de dois pontos ordenada no tempo (aquela que vem da integral do caminho):
- ∂ ∂ 2? ? (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...δ δ (x){displaystyle partial ^{2}Delta (x)=idelta (x),}
Para que:
- ? ? (k)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...k2{displaystyle Delta (k)={frac {i}{k^{2}}
Se as equações de movimento forem lineares, o propagador será sempre o recíproco da matriz de forma quadrática que define o Lagrangeano livre, pois isso dá as equações de movimento. Isso também é fácil de ver diretamente da integral de caminho. O fator de i desaparece na teoria euclidiana.
Teorema de Wick
Como cada modo de campo é um gaussiano independente, os valores esperados para o produto de muitos modos de campo obedecem ao teorema de Wick:
- ⟨φ φ (k1)φ φ (k2)⋯ ⋯ φ φ (kn)){displaystyle leftlangle phi (k_{1})phi (k_{2})cdots phi (k_{n})rightrangle }
é zero, a menos que os modos de campo coincidam em pares. Isso significa que é zero para um número ímpar de φ e para um número par de φ, é igual a uma contribuição de cada par separadamente, com uma função delta.
- ⟨φ φ (k1)⋯ ⋯ φ φ (k2n))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento ? ? Eu...,JJδ δ (kEu...- Sim. - Sim. kJJ)kEu...2{displaystyle leftlangle phi (k_{1})cdots phi (k_{2n})rightrangle =sum prod _{i,j}{frac {delta left (k_{i}-k_{j}right)}{k_{i}^{2}}}}
onde a soma é sobre cada partição dos modos de campo em pares, e o produto é sobre os pares. Por exemplo,
- ⟨φ φ (k1)φ φ (k2)φ φ (k3)φ φ (k4))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ (k1- Sim. - Sim. k2)k12δ δ (k3- Sim. - Sim. k4)k32+δ δ (k1- Sim. - Sim. k3)k32δ δ (k2- Sim. - Sim. k4)k22+δ δ (k1- Sim. - Sim. k4)k12δ δ (k2- Sim. - Sim. k3)k22{displaystyle leftlangle phi (k_{1})phi (k_{2})phi (k_{3})phi (k_{4})rightrangle ={frac {delta (k_{1}-k_{2})}{k_{1}^{2}}}{frac Não. (k_{3}-k_{4})}{k_{3}^{2}}}+{frac Não. (k_{1}-k_{3})}{k_{3}^{2}}}{frac Não. (k_{2}-k_{4})}{k_{2}^{2}}}+{frac Não. (k_{1}-k_{4})}{k_{1}^{2}}}{frac Não. (k_{2}-k_{3})}{k_{2}^{2}}}}
Uma interpretação do teorema de Wick é que cada inserção de campo pode ser considerada como uma linha pendente, e o valor esperado é calculado ligando as linhas em pares, colocando um fator de função delta que garante que o momento de cada parceiro no par é igual, e dividindo pelo propagador.
Momentos gaussianos superiores — completando o teorema de Wick
Há um ponto sutil deixado antes que o teorema de Wick seja provado - e se mais de dois φ φ - Sim.Tem o mesmo impulso? Se for um número ímpar, a integral é zero; os valores negativos cancelam com os valores positivos. Mas se o número for igual, a integral é positiva. A demonstração anterior assumiu que o φ φ - Sim.s só corresponderia em pares.
Mas o teorema é correto mesmo quando arbitrariamente muitos dos φ φ - Sim. são iguais, e esta é uma propriedade notável da integração gaussiana:
- Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ e- Sim. - Sim. umx2/2Dx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2D D um{displaystyle I=int e^{-ax^{2}/2}dx={sqrt {2pi }{a}}
- ∂ ∂ n∂ ∂ umnEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ x2n2ne- Sim. - Sim. umx2/2Dx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1)) 3)) 5...... )) (2n- Sim. - Sim. 1)2)) 2)) 2...... )) 22D D um- Sim. - Sim. 2n+12{displaystyle {frac {partial ^{n}}{partial a^{n}}}I=int {x^{2n}}{2^{n}}}e^{-ax^{2}/2}dx={frac {1cdot 3cdot 5ldots cdot (2n-1)}{2cdot 2cdot 2ldots ;;;;;cdot 2;;;;;;}}{sqrt {2pi }},a^{-{frac {2n+1}{2}}
Dividindo por I,
- ⟨x2n)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ x2ne- Sim. - Sim. umx2/2∫ ∫ e- Sim. - Sim. umx2/2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1)) 3)) 5...... )) (2n- Sim. - Sim. 1)1umn{displaystyle leftlangle} x^{2n}rightrangle ={frac {displaystyle int x^{2n}e^{-ax^{2}/2}}{displaystyle int e^{-ax^{2}/2}}}=1cdot 3cdot 5ldots cdot (2n-1){frac {1}{a^{n}}}}}}}}
- ⟨x2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1um{displaystyle leftlangle x^{2}rightrangle ={frac Não.
Se o teorema de Wick estivesse correto, os momentos mais altos seriam dados por todos os pares possíveis de uma lista de 2n diferentes x:
- ⟨x1x2x3⋯ ⋯ x2n){displaystyle leftlangle} x_{1}x_{2}x_{3}cdots x_{2n}rightrangle }
onde os x são todos a mesma variável, o índice é apenas para acompanhar o número de maneiras de emparelhá-los. O primeiro x pode ser emparelhado com 2n − 1 outros, deixando 2n − 2. O próximo x não pareado pode ser pareado com 2n − 3 diferentes x deixando 2n − 4, e assim por diante. Isso significa que o teorema de Wick, não corrigido, diz que o valor esperado de x2n deve ser:
- ⟨x2n)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(2n- Sim. - Sim. 1))) (2n- Sim. - Sim. 3)...... )) 5)) 3)) 1⟨x2)n{displaystyle leftlangle x^{2n}rightrangle =(2n-1)cdot (2n-3)ldots cdot 5cdot 3cdot 1leftlangle x^{2}rightrangle ^{n}}
e esta é de fato a resposta correta. Portanto, o teorema de Wick é válido, não importa quantos momentos das variáveis internas coincidam.
Interação
As interações são representadas por contribuições de ordem superior, pois as contribuições quadráticas são sempre gaussianas. A interação mais simples é a auto-interação quártica, com uma ação:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ ∂ ∂ μ μ φ φ ∂ ∂ μ μ φ φ +λ λ 4!φ φ 4.Não. S=int partial ^{mu }phi partial _{mu }phi +{frac Não. }{4!}}phi ^{4}
A razão do fator combinatório 4! ficará claro em breve. Escrevendo a ação em termos dos modos de Fourier da rede (ou contínuo):
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ kk2|φ φ (k)|2+λ λ 4!∫ ∫ k1k2k3k4φ φ (k1)φ φ (k2)φ φ (k3)φ φ (k4)δ δ (k1+k2+k3+k4)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =SF+X.Não. S. _{k}k^{2}left|phi (k)right|^{2}+{frac {lambda }{4! _{k_{1}k_{2}k_{3}k_{4}}phi (k_{1})phi (k_{2})phi (k_{3})phi (k_{4})delta (k_{1}+k_{2}+k_{3}+k_{4})=S_{F}+X.}
Onde SF é a ação livre, cujas funções de correlação são dadas por Wick' teorema. A exponencial de S na integral de caminho pode ser expandida em potências de λ, dando uma série de correções à ação livre.
- e- Sim. - Sim. S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e- Sim. - Sim. SF(1+X+12!XX+13!XXX+⋯ ⋯ ){displaystyle e^{-S}=e^{-S_{F}}left(1+X+{frac {1}{2!}}XX+{frac {1}{3!}}XX+cdots right)}
A integral do caminho para a ação de interação é então uma série de potências de correções para a ação livre. O termo representado por X deve ser pensado como quatro meias-linhas, uma para cada fator de φ(k). As meias linhas se encontram em um vértice, o que contribui com uma função delta que garante que a soma dos momentos sejam todos iguais.
Para calcular uma função de correlação na teoria de interação, há uma contribuição dos termos X agora. Por exemplo, a integral de caminho para o correlacionador de quatro campos:
- ⟨φ φ (k1)φ φ (k2)φ φ (k3)φ φ (k4))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ e- Sim. - Sim. Sφ φ (k1)φ φ (k2)φ φ (k3)φ φ (k4)Dφ φ Z.{displaystyle leftlangle phi (k_{1})phi (k_{2})phi (k_{3})phi (k_{4})rightrangle ={frac {displaystyle int e^{-S}phi (k_{1})phi (k_{2})phi (k_{4})phi (k_{4})Dphi ?
que no campo livre era apenas diferente de zero quando os momentos k eram iguais em pares, agora é diferente de zero para todos os valores de k. Os momentos das inserções φ(ki) agora podem corresponder aos momentos dos Xs na expansão. As inserções também devem ser pensadas como meias-linhas, quatro neste caso, que carregam um momento k, mas que é não integrado.
A contribuição de ordem mais baixa vem do primeiro termo não trivial e−SF X na expansão Taylor da ação. O teorema de Wick requer que os momentos nas X meias-linhas, as φ(k) em X, devem corresponder aos momentos das meias-linhas externas em pares. A nova contribuição é igual a:
- λ λ 1k121k221k321k42.{displaystyle lambda} {1}{k_{1}^{2}}}{frac {1}{k_{2}^{2}}}{frac {1}{k_{3}^{2}}}{frac {1}{k_{4}^{2}}},.}
Os 4! dentro de X é cancelado porque existem exatamente 4! maneiras de combinar as meias-linhas em X com as meias-linhas externas. Cada uma dessas maneiras diferentes de combinar as meias-linhas em pares contribui exatamente uma vez, independentemente dos valores de k1,2,3,4, pelo teorema de Wick.
Diagramas de Feynman
A expansão da ação em potências de X dá uma série de termos com número progressivamente maior de Xs. A contribuição do termo com exatamente n Xs é chamado nª ordem.
O nésima ordem tem:
- 4n meias linhas internas, que são os fatores de φ(k) do XS. Estes todos terminam em um vértice, e são integrados sobre todo possível k.
- meias-linhas externas, que são a vinda do φ(k) inserções na integral.
Pelo teorema de Wick, cada par de meias-linhas deve ser emparelhado para formar uma linha, e essa linha fornece um fator de
- δ δ (k1+k2)k12- Não. (k_{1}+k_{2})}{k_{1}^{2}}
que multiplica a contribuição. Isso significa que as duas meias-linhas que formam uma linha são forçadas a ter momento igual e oposto. A própria linha deve ser rotulada por uma seta, desenhada paralelamente à linha e rotulada pelo momento na linha k. A meia linha no final da seta carrega o momento k, enquanto a meia linha no final da seta carrega o momento -k. Se uma das duas meias-linhas for externa, isso mata a integral sobre o k, pois força o k para ser igual ao externo k. Se ambos forem internos, a integral sobre k permanece.
Os diagramas que são formados ligando as meias-linhas nos Xs com as meias-linhas externas, representando inserções, são os diagramas de Feynman desta teoria. Cada linha carrega um fator de 1/k2, o propagador, e vai de vértice a vértice, ou termina em uma inserção. Se for interno, é integrado. Em cada vértice, o total de entrada k é igual ao total de saída k.
O número de maneiras de fazer um diagrama unindo meias-linhas em linhas cancela quase completamente os fatores fatoriais provenientes da série de Taylor do exponencial e do 4! em cada vértice.
Ordem do loop
Um diagrama de floresta é aquele em que todas as linhas internas têm momento que é completamente determinado pelas linhas externas e a condição de que o momento de entrada e saída sejam iguais em cada vértice. A contribuição destes diagramas é um produto de propagadores, sem nenhuma integração. Um diagrama de árvore é um diagrama de floresta conectado.
Um exemplo de diagrama de árvore é aquele em que cada uma das quatro linhas externas termina em um X. Outra é quando três linhas externas terminam em um X, e a meia linha restante se junta a outra X, e as meias-linhas restantes deste X correr para linhas externas. Todos esses também são diagramas de floresta (já que toda árvore é uma floresta); um exemplo de uma floresta que não é uma árvore é quando oito linhas externas terminam em dois Xs.
É fácil verificar que em todos esses casos, os momentos em todas as linhas internas são determinados pelos momentos externos e pela condição de conservação do momento em cada vértice.
Um diagrama que não é um diagrama de floresta é chamado de diagrama loop, e um exemplo é aquele em que duas linhas de um X são unidos a linhas externas, enquanto as duas linhas restantes são unidas entre si. As duas linhas unidas uma à outra podem ter qualquer momento, já que ambas entram e saem do mesmo vértice. Um exemplo mais complicado é aquele em que dois Xs são unidos combinando as pernas uma com a outra. Este diagrama não tem linhas externas.
A razão pela qual os diagramas de loop são chamados de diagramas de loop é porque o número de k-integrais que são deixados indeterminados pela conservação do momento é igual ao número de loops fechados independentes no diagrama, onde os loops independentes são contados como na teoria da homologia. A homologia é de valor real (na verdade Rd valorizada), o valor associado a cada linha é o momento. O operador de limite leva cada linha à soma dos vértices finais com um sinal positivo na cabeça e um sinal negativo na cauda. A condição de que o momento é conservado é exatamente a condição de que o limite do gráfico ponderado com valor k é zero.
Um conjunto de k-valores válidos pode ser redefinido arbitrariamente sempre que houver um loop fechado. Um loop fechado é um caminho cíclico de vértices adjacentes que nunca revisita o mesmo vértice. Tal ciclo pode ser pensado como o limite de uma hipotética 2 células. Os rótulos k de um gráfico que conserva o momento (ou seja, que tem limite zero) até redefinições de k (ou seja, até limites de 2 células) definem a primeira homologia de um gráfico. O número de momentos independentes que não são determinados é então igual ao número de loops de homologia independentes. Para muitos gráficos, isso é igual ao número de loops contados da maneira mais intuitiva.
Fatores de simetria
O número de maneiras de formar um determinado diagrama de Feynman unindo meias linhas é grande e, pelo teorema de Wick, cada maneira de emparelhar as meias linhas contribui igualmente. Frequentemente, isso cancela completamente os fatoriais no denominador de cada termo, mas às vezes o cancelamento é incompleto.
O denominador não cancelado é chamado de fator de simetria do diagrama. A contribuição de cada diagrama para a função de correlação deve ser dividida pelo seu fator de simetria.
Por exemplo, considere o diagrama de Feynman formado por duas linhas externas unidas a um X, e as duas meias-linhas restantes no X unidos entre si. Existem 4 × 3 maneiras de unir as meias-linhas externas ao X, e só há uma maneira de unir o duas linhas restantes entre si. O X vem dividido por 4! = 4 × 3 × 2, mas o número de maneiras de ligar as X meias linhas para fazer o diagrama é apenas 4 × 3, então a contribuição deste diagrama é dividida por dois.
Para outro exemplo, considere o diagrama formado unindo todas as meias-linhas de um X a todas as meias-linhas de outro X. Este diagrama é chamado de bolha de vácuo, porque não se liga a nenhuma linha externa. Existem 4! maneiras de formar este diagrama, mas o denominador inclui um 2! (da expansão do exponencial, há dois Xs) e dois fatores de 4!. A contribuição é multiplicada por 4!/2 × 4! × 4! = 1/ 48.
Outro exemplo é o diagrama de Feynman formado por dois Xs onde cada X vincula até duas linhas externas e as duas meias linhas restantes de cada X são unidos entre si. O número de maneiras de vincular um X a duas linhas externas é 4 × 3 e X poderia se conectar a qualquer par, dando um fator adicional de 2. As duas meias-linhas restantes nos dois Xs podem ser ligados entre si de duas maneiras, de modo que o número total de maneiras de formar o diagrama seja 4 × 3 × 4 × 3 × 2 × 2, enquanto o denominador é 4! × 4! × 2!. O fator de simetria total é 2, e a contribuição deste diagrama é dividida por 2.
O teorema do fator de simetria fornece o fator de simetria para um diagrama geral: a contribuição de cada diagrama de Feynman deve ser dividida pela ordem de seu grupo de automorfismos, o número de simetrias que possui.
Um automorfismo de um grafo de Feynman é uma permutação M das linhas e uma permutação N dos vértices com as seguintes propriedades:
- Se uma linha Eu... vai de vértice v ao vértice V., então M(Eu...) de N(v) para N(V.). Se a linha é não direcionada, como é para um campo escalar real, então M(Eu...) pode ir N(V.) para N(v) também.
- Se uma linha Eu... termina em uma linha externa, M(Eu...) termina na mesma linha externa.
- Se houver diferentes tipos de linhas, M(Eu...) deve preservar o tipo.
Este teorema tem uma interpretação em termos de caminhos de partículas: quando partículas idênticas estão presentes, a integral sobre todas as partículas intermediárias não deve contar duas vezes os estados que diferem apenas pela troca de partículas idênticas.
Prova: Para provar este teorema, rotule todas as linhas internas e externas de um diagrama com um nome exclusivo. Em seguida, forme o diagrama ligando uma meia linha a um nome e depois à outra meia linha.
Agora conte o número de maneiras de formar o diagrama nomeado. Cada permutação dos Xs fornece um padrão diferente de ligar nomes a meias-linhas, e isso é um fator de n!. Cada permutação das meias-linhas em um único X dá um fator de 4!. Assim, um diagrama nomeado pode ser formado exatamente de tantas maneiras quanto o denominador da expansão de Feynman.
Mas o número de diagramas não nomeados é menor que o número de diagramas nomeados pela ordem do grupo de automorfismo do grafo.
Diagramas conectados: teorema do cluster vinculado
A grosso modo, um diagrama de Feynman é chamado de conectado se todos os vértices e linhas propagadoras estiverem ligados por uma sequência de vértices e propagadores do próprio diagrama. Se alguém vê-lo como um grafo não direcionado, ele é conectado. A notável relevância de tais diagramas em QFTs se deve ao fato de serem suficientes para determinar a função de partição quântica Z[J]. Mais precisamente, os diagramas de Feynman conectados determinam
- Eu...WNão.JJ])) I Z.Não.JJ].{displaystyle iW[J]equiv ln Z[J].}
Para ver isso, deve-se lembrar que
- Z.Não.JJ]∝ ∝ Gerenciamento Gerenciamento kDk{displaystyle Z[J]propto sum _{k}{D_{k}}}
com Dk construído a partir de algum diagrama de Feynman (arbitrário) que pode ser pensado para consistir de vários componentes conectados Ci. Se alguém encontrar cópias ni (idênticas) de um componente Ci dentro do diagrama de Feynman Dk é necessário incluir um fator de simetria n i!. No entanto, no final, cada contribuição de um diagrama de Feynman Dk para a função de partição tem o genérico forma
- ? ? Eu...CEu...nEu...nEu...!{displaystyle prod _{i}{frac {C_{i}^{n_{i}}}{n_{i}!}}}
onde i rotula os (infinitamente) muitos diagramas de Feynman conectados possíveis.
Um esquema para criar sucessivamente tais contribuições do Dk ao Z[J] é obtido por
- (10!+C11!+C122!+⋯ ⋯ )(1+C2+12C22+⋯ ⋯ )⋯ ⋯ {displaystyle left({frac) {1}{0!}}+{frac {C_{1}}{1!}}+{frac {C_{1}^{2}}{2!}}+cdots right)left(1+C_{2}+{frac {1}{2}}C_{2}^{2}+cdots right)cdots }
e, portanto, produz
- Z.Não.JJ]∝ ∝ ? ? Eu...Gerenciamento Gerenciamento nEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0∞ ∞ CEu...nEu...nEu...!= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =exp Gerenciamento Gerenciamento Eu...CEu...∝ ∝ exp WNão.JJ].{displaystyle Z[J]propto prod _{i}{sum _{n_{i}=0}^{infty ? {C_{i}^{n_{i}}}{n_{i}!}}}=exp Sim. _{i}{C_{i}}}propto exp {W[J]},.}
Para estabelecer a normalização Z0 = exp W[0 ] = 1 calcula-se simplesmente todos os diagramas de vácuo conectados, ou seja, os diagramas sem quaisquer fontes J (às vezes referido como pernas externas de um diagrama de Feynman).
Bolhas de vácuo
Uma consequência imediata do teorema do cluster vinculado é que todas as bolhas de vácuo, diagramas sem linhas externas, se cancelam ao calcular as funções de correlação. Uma função de correlação é dada por uma razão de integrais de caminho:
- ⟨φ φ 1(x1)⋯ ⋯ φ φ n(xn))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ e- Sim. - Sim. Sφ φ 1(x1)⋯ ⋯ φ φ n(xn)Dφ φ ∫ ∫ e- Sim. - Sim. SDφ φ .{displaystyle leftlangle phi _{1}(x_{1})cdots phi _{n}(x_{n})rightrangle ={frac {displaystyle int e^{-S}phi _{1}(x_{1})cdots phi _{n}(x_{n}),Dphi }{displaystyle int} e^{S }},.}
O topo é a soma de todos os diagramas de Feynman, incluindo diagramas desconectados que não se conectam a linhas externas. Em termos dos diagramas conectados, o numerador inclui as mesmas contribuições das bolhas de vácuo que o denominador:
- ∫ ∫ e- Sim. - Sim. Sφ φ 1(x1)⋯ ⋯ φ φ n(xn)Dφ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(Gerenciamento Gerenciamento EEu...)(exp (Gerenciamento Gerenciamento Eu...CEu...)).{displaystyle int e^{-S}phi _{1}(x_{1})cdots phi _{n}(x_{n}),Dphi =left(sum E_{i}right)left(exp left(sum _{i}C_{i}right)right),.}
Onde a soma dos diagramas E inclui apenas aqueles diagramas cujos componentes conectados terminam em pelo menos uma linha externa. As bolhas de vácuo são as mesmas quaisquer que sejam as linhas externas e fornecem um fator multiplicativo geral. O denominador é a soma de todas as bolhas de vácuo e a divisão elimina o segundo fator.
As bolhas de vácuo são úteis apenas para determinar o próprio Z, que a partir da definição da integral do caminho é igual a:
- Z.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ e- Sim. - Sim. SDφ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e- Sim. - Sim. H. H. H.T= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e- Sim. - Sim. ? ? V{displaystyle Z=int e^{-S}Dphi =e^{-HT}=e^{-rho V.
onde ρ é a densidade de energia no vácuo. Cada bolha de vácuo contém um fator de δ(k) zerando o total k em cada vértice, e quando não há linhas externas, contém um fator de δ(0) , porque a conservação do momento é superaplicada. Em volume finito, esse fator pode ser identificado como o volume total do espaço-tempo. Dividindo pelo volume, a integral restante para a bolha de vácuo tem uma interpretação: é uma contribuição para a densidade de energia do vácuo.
Fontes
As funções de correlação são a soma dos diagramas de Feynman conectados, mas o formalismo trata os diagramas conectados e desconectados de maneira diferente. Linhas internas terminam em vértices, enquanto linhas externas partem para inserções. A introdução de fontes unifica o formalismo, criando novos vértices onde uma linha pode terminar.
Fontes são campos externos, campos que contribuem para a ação, mas não são variáveis dinâmicas. Uma fonte de campo escalar é outro campo escalar h que contribui com um termo para o (Lorentz) Lagrangiano:
- ∫ ∫ h(x)φ φ (x)DDx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ h(k)φ φ (k)DDk{displaystyle int h(x)phi (x),d^{d}x=int h(k)phi (k),d^{d}k,}
Na expansão de Feynman, isso contribui com H termos com uma meia linha terminando em um vértice. As linhas em um diagrama de Feynman agora podem terminar em um vértice X ou em um H e apenas uma linha entra em um vértice H. A regra de Feynman para um vértice H é que uma linha de um vértice H com momento k obtém um fator de h(k).
A soma dos diagramas conectados na presença de fontes inclui um termo para cada diagrama conectado na ausência de fontes, exceto que agora os diagramas podem terminar na fonte. Tradicionalmente, uma fonte é representada por um pequeno "×" com uma linha se estendendo, exatamente como uma inserção.
- log (Z.Não.h])= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento n,Ch(k1)h(k2)⋯ ⋯ h(kn)C(k1,⋯ ⋯ ,kn)(}Z[h]{big)}=sum _{n,C}h(k_{1})h(k_{2})cdots h(k_{n})C(k_{1},cdotsk_{n}),}
onde C(k1,...,kn ) é o diagrama conectado com n linhas externas carregando momento conforme indicado. A soma é sobre todos os diagramas conectados, como antes.
O campo h não é dinâmico, o que significa que não há caminho integral sobre h: h é apenas um parâmetro no Lagrangeano, que varia de ponto a ponto. A integral de caminho para o campo é:
- Z.Não.h]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ eEu...S+Eu...∫ ∫ hφ φ Dφ φ {displaystyle Z[h]=int e^{iS+iint hphi },Dphi ,}
e é uma função dos valores de h em cada ponto. Uma maneira de interpretar essa expressão é que ela está tomando a transformada de Fourier no espaço de campo. Se houver uma densidade de probabilidade em Rn, a transformada de Fourier da densidade de probabilidade é:
- ∫ ∫ ? ? (Sim.)eEu...kSim.DnSim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨eEu...kSim.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨? ? Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1neEu...hEu...Sim.Eu...){displaystyle int rho (y)e^{iky},d^{n}y=leftlangle e^{iky}rightrangle =leftlangle prod _{i=1}^{n}e^{ih_{i}y_{i}}rightrangle ,}
A transformada de Fourier é a expectativa de uma exponencial oscilatória. A integral do caminho na presença de uma fonte h(x) é:
- Z.Não.h]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ eEu...SeEu...∫ ∫ xh(x)φ φ (x)Dφ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨eEu...hφ φ ){displaystyle Z[h]=int e^{iS}e^{iint _{x}h(x)phi (x)}, Dphi =leftlangle e^{ihphi }rightrangle }
que, em uma rede, é o produto de uma exponencial oscilatória para cada valor de campo:
- ⟨? ? xeEu...hxφ φ x){displaystyle leftlangle prod _{x}e^{ih_{x}phi _{x}}rightrangle }
A transformada de Fourier de uma função delta é uma constante, que fornece uma expressão formal para uma função delta:
- δ δ (x- Sim. - Sim. Sim.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ eEu...k(x- Sim. - Sim. Sim.)Dk{displaystyle delta (x-y)=int e^{ik(x-y)},dk}
Isso diz a você como é uma função delta de campo em uma integral de caminho. Para dois campos escalares φ e η,
- δ δ (φ φ - Sim. - Sim. ? ? )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ eEu...h(x)(φ φ (x)- Sim. - Sim. ? ? (x))DDxDh,{displaystyle delta (phi -eta)=int e^{ih(x){big (}phi (x)-eta (x){big)},d^{d}x}, Dh,
que integra sobre a coordenada da transformada de Fourier, sobre h. Essa expressão é útil para alterar formalmente as coordenadas de campo na integral de caminho, da mesma forma que uma função delta é usada para alterar as coordenadas em uma integral multidimensional comum.
A função de partição agora é uma função do campo h, e a função de partição física é o valor quando h é a função zero:
As funções de correlação são derivadas da integral de caminho em relação à fonte:
- ⟨φ φ (x))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Z.∂ ∂ ∂ ∂ h(x)Z.Não.h]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ ∂ ∂ h(x)log (Z.Não.h]).{displaystyle leftlangle phi (x)rightrangle ={frac {1}{Z}}{frac {partial }{partial h(x)}}Z[h]={frac {partial }{partial h(x)}}log {big (}Z[h]{big)},.}
No espaço euclidiano, as contribuições da fonte para a ação ainda podem aparecer com um fator de i, de modo que ainda fazem um Transformada de Fourier.
Girar 1/2; e#34;prótons#34; e "fantasmas n#34;
Spin 1/2: integrais de Grassmann
A integral do caminho de campo pode ser estendida para o caso de Fermi, mas somente se a noção de integração for expandida. Uma integral de Grassmann de um campo de Fermi livre é um determinante de alta dimensão ou Pfaffiano, que define o novo tipo de integração gaussiana apropriada para campos de Fermi.
As duas fórmulas fundamentais da integração de Grassmann são:
- ∫ ∫ eMEu...JJ? ? ? ? Eu...? ? JJD? ? ? ? D? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =De)(M),{displaystyle int e^{M_{ij}{bar {psi }}^{i}psi ^{j}},D{bar {psi }},Dpsi =mathrm {Det} (M),}
onde M é uma matriz arbitrária e ψ, ψ são variáveis Grassmann independentes para cada índice i, e
- ∫ ∫ e12AEu...JJ? ? Eu...? ? JJD? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Pfumff(A),{displaystyle int e^{{frac {1}{2}}A_{ij}psi ^{i}psi ^{j}},Dpsi =mathrm (A),
onde A é uma matriz antissimétrica, ψ é uma coleção de variáveis Grassmann, e o 1/2 é evitar contagem dupla (já que ψiψj = −ψjψi).
Na notação de matriz, onde ψ e η são vetores de linha com valor de Grassmann, η e ψ são Grassmann- vetores de coluna com valor, e M é uma matriz com valor real:
- Z.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ e? ? ? ? M? ? +? ? ? ? ? ? +? ? ? ? ? ? D? ? ? ? D? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ e(? ? ? ? +? ? ? ? M- Sim. - Sim. 1)M(? ? +M- Sim. - Sim. 1? ? )- Sim. - Sim. ? ? ? ? M- Sim. - Sim. 1? ? D? ? ? ? D? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =De)(M)e- Sim. - Sim. ? ? ? ? M- Sim. - Sim. 1? ? ,{displaystyle Z=int e^{{bar {psi }}Mpsi +{bar {eta }}psi +{bar {psi }}eta },D{bar {psi }}, Dpsi =int e^{left({bar {psi }}+ }}M^{-1}right)Mleft(psi +M^{-1}eta right)-{bar {eta }}M^{-1}eta },D{bar {psi }}, Dpsi =mathrm (Det) (M)e^{-{bar }}M^{-1}eta },}
onde a última igualdade é consequência da invariância de translação da integral de Grassmann. As variáveis Grassmann η são fontes externas para ψ, e diferenciando em relação a η reduz os fatores de ψ.
- ⟨? ? ? ? ? ? )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Z.∂ ∂ ∂ ∂ ? ? ∂ ∂ ∂ ∂ ? ? ? ? Z.|? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =M- Sim. - Sim. 1{displaystyle leftlangle {bar {psi }}psi rightrangle ={frac {1}{Z}}{frac {partial }{partial eta }}{frac {partial }{partial {displaystyle }{partial {bar {paral } }}Z|_{eta ={bar }}=0}=M^{-1}}
novamente, em uma notação de matriz esquemática. O significado da fórmula acima é que a derivada em relação ao componente apropriado de η e η fornece o elemento de matriz de M -1. Isso é exatamente análogo à fórmula de integração do caminho bosônico para uma integral gaussiana de um campo bosônico complexo:
- ∫ ∫ eφ φ ∗ ∗ Mφ φ +h∗ ∗ φ φ +φ φ ∗ ∗ hDφ φ ∗ ∗ Dφ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =eh∗ ∗ M- Sim. - Sim. 1hDe)(M){displaystyle int e^{phi ^{*}Mphi +h^{*}phi +phi ^{*}h}, Dphi ^{*}, Dphi ={frac {e^{h^{*}M^{-1}h}}{mathrm (Det)
- ⟨φ φ ∗ ∗ φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Z.∂ ∂ ∂ ∂ h∂ ∂ ∂ ∂ h∗ ∗ Z.|h= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =h∗ ∗ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =M- Sim. - Sim. 1.{displaystyle leftlangle phi ^{*}phi rightrangle ={frac {1}{Z}}{frac (partial) h) - Não. h^{*}}}Z|_{h=h^{*}=0}=M^{-1},.}
De forma que o propagador é o inverso da matriz na parte quadrática da ação tanto no caso de Bose quanto no de Fermi.
Para campos de Grassmann reais, para férmions de Majorana, a integral de caminho é um Pfaffiano vezes uma forma quadrática de origem, e as fórmulas fornecem a raiz quadrada do determinante, assim como para campos bosônicos reais. O propagador ainda é o inverso da parte quadrática.
O Dirac Lagrangeano livre:
- ∫ ∫ ? ? ? ? (γ γ μ μ ∂ ∂ μ μ - Sim. - Sim. m)? ? {displaystyle int {bar {psi }}left(gamma ^{mu }partial _{mu }-mright)psi }
formalmente fornece as equações de movimento e as relações de anticomutação do campo de Dirac, assim como o Klein Gordon Lagrangiano em uma integral de caminho comum fornece as equações de movimento e as relações de comutação do campo escalar. Usando a transformada espacial de Fourier do campo de Dirac como uma nova base para a álgebra de Grassmann, a parte quadrática da ação de Dirac torna-se simples de inverter:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ k? ? ? ? (Eu...γ γ μ μ kμ μ - Sim. - Sim. m)? ? .Não. S=int _{k}{bar {psi }}left(igamma ^{mu - Sim. }-mright)psi ,.}
O propagador é o inverso da matriz M ligando ψ(k) e ψ (k), pois valores diferentes de k não se misturam.
- ⟨? ? ? ? (k?)? ? (k))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ (k+k?)1γ γ )) k- Sim. - Sim. m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ (k+k?)γ γ )) k+mk2- Sim. - Sim. m2{displaystyle leftlangle {bar {psi }}(k')psi (k)rightrangle =delta (k+k'){frac {1}{gamma cdot k-m}}=delta (k+k'){frac {gamma cdot k+m}{k^{2}-m^{2}}}}
O análogo do teorema de Wick corresponde a ψ e ψ em pares:
- ⟨? ? ? ? (k1)? ? ? ? (k2)⋯ ⋯ ? ? ? ? (kn)? ? (k1?)⋯ ⋯ ? ? (kn))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento pumEu...REu...ngS(- Sim. - Sim. 1)S? ? pumEu...RSEu...,JJδ δ (kEu...- Sim. - Sim. kJJ)1γ γ )) kEu...- Sim. - Sim. m{displaystyle leftlangle {bar {psi }}(k_{1}){bar {psi }}(k_{2})cdots {bar {psi }}(k_{n})psi (k'_{1})cdots left (k_{n})rightrangle =sum _{mathrm {pairings} } O que é isso? k_{i}-m}}}
onde S é o sinal da permutação que reordena a sequência de ψ e ψ para colocar os que estão emparelhados para fazer as funções delta próximas umas das outras, com o ψ vindo logo antes do ψ. Como um par ψ, ψ é um elemento de comutação da álgebra de Grassmann, não importa em que ordem os pares estão. Se mais de um ψ, ψ têm o mesmo k, a integral é zero, e é fácil verificar que a soma dos pares dá zero neste caso (há sempre um número par deles). Este é o análogo de Grassmann dos momentos gaussianos superiores que completaram o teorema Bosonic Wick anteriormente.
As regras para spin-1/ 2 As partículas de Dirac são as seguintes: o propagador é o inverso do operador de Dirac, as linhas têm setas como para um campo escalar complexo e o diagrama adquire uma fator global de -1 para cada loop de Fermi fechado. Se houver um número ímpar de loops de Fermi, o diagrama muda de sinal. Historicamente, a regra −1 foi muito difícil para Feynman descobrir. Ele o descobriu depois de um longo processo de tentativa e erro, pois não tinha uma teoria adequada da integração de Grassmann.
A regra decorre da observação de que o número de linhas de Fermi em um vértice é sempre par. Cada termo no lagrangiano deve ser sempre bosônico. Um loop de Fermi é contado seguindo as linhas Fermiônicas até que se retorne ao ponto de partida, removendo essas linhas do diagrama. A repetição desse processo eventualmente apaga todas as linhas fermiônicas: esse é o algoritmo de Euler para 2 cores em um gráfico, que funciona sempre que cada vértice tem grau par. O número de passos no algoritmo de Euler é apenas igual ao número de ciclos independentes de homologia Fermiônica no caso especial comum de que todos os termos no Lagrangiano são exatamente quadráticos nos campos de Fermi, de forma que cada vértice tem exatamente duas linhas Fermiônicas. Quando há quatro interações de Fermi (como na teoria efetiva de Fermi das interações nucleares fracas), há mais k-integrais do que Loops de Fermi. Neste caso, a regra de contagem deve aplicar o algoritmo de Euler emparelhando as linhas de Fermi em cada vértice em pares que juntos formam um fator bosônico do termo no Lagrangeano, e ao inserir um vértice por uma linha, o algoritmo deve sempre deixar com a linha de parceiros.
Para esclarecer e provar a regra, considere um diagrama de Feynman formado por vértices, termos no Lagrangeano, com campos de Fermions. O termo completo é bosônico, é um elemento comutável da álgebra de Grassmann, então a ordem em que os vértices aparecem não é importante. As linhas de Fermi estão ligadas em loops e, ao percorrer o loop, pode-se reordenar os termos do vértice um após o outro, sem nenhum custo de sinal. A exceção é quando você retorna ao ponto de partida, e a meia-linha final deve ser unida à primeira meia-linha desvinculada. Isso requer uma permutação para mover o último ψ para vá na frente do primeiro ψ, e isso dá o sinal.
Esta regra é o único efeito visível do princípio de exclusão nas linhas internas. Quando há linhas externas, as amplitudes são antisimétricas quando duas inserções de Fermi para partículas idênticas são trocadas. Isso é automático no formalismo da fonte, porque as próprias fontes dos campos de Fermi são valores de Grassmann.
Giro 1: fótons
O propagador ingênuo para fótons é infinito, pois o Lagrangeano para o campo A é:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 14Fμ μ Processo Processo Fμ μ Processo Processo = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ - Sim. - Sim. 12(∂ ∂ μ μ AProcesso Processo ∂ ∂ μ μ AProcesso Processo - Sim. - Sim. ∂ ∂ μ μ Aμ μ ∂ ∂ Processo Processo AProcesso Processo ).Não. - Não. {1}{4}}F^{mu nu }F_{mu nu }=int -{tfrac {1}{2}}left(partial ^{mu }A_{nu }partial _{mu }A^{nu }-partial ^{mu }A_{mu }partial _{nu }A^{nu }right),.}
A forma quadrática que define o propagador não é invertível. A razão é a invariância de calibre do campo; adicionar um gradiente a A não altera a física.
Para corrigir esse problema, é preciso consertar um medidor. A maneira mais conveniente é exigir que a divergência de A seja alguma função f, cujo valor é aleatório ponto a ponto. Não faz mal integrar sobre os valores de f, pois isso apenas determina a escolha da bitola. Este procedimento insere o seguinte fator na integral do caminho para A:
- ∫ ∫ δ δ (∂ ∂ μ μ Aμ μ - Sim. - Sim. f)e- Sim. - Sim. f22Df.{displaystyle int delta left(partial _{mu }A^{mu }-fright)e^{-{frac {f^{2}}{2}}},Df,.}
O primeiro fator, a função delta, fixa o medidor. O segundo fator soma valores diferentes de f que são fixações de medidores inequivalentes. Isso é simplesmente
- e- Sim. - Sim. (∂ ∂ μ μ Aμ μ )22.{displaystyle e^{-{frac {left(partial _{mu }A_{mu }right)^{2}}{2}}},.}
A contribuição adicional da fixação do medidor cancela a segunda metade do lagrangeano livre, dando ao lagrangiano de Feynman:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ ∂ ∂ μ μ AProcesso Processo ∂ ∂ μ μ AProcesso Processo Não. S=int partial ^{mu }A^{nu }partial _{mu }A_{nu }}
que é como quatro campos escalares livres independentes, um para cada componente de A. O propagador de Feynman é:
- ⟨Aμ μ (k)AProcesso Processo (k?))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ (k+k?)gμ μ Processo Processo k2.{displaystyle leftlangle A_{mu }(k)A_{nu }(k')rightrangle =delta left(k+k'right){frac {g_{mu nu }}{k^{2}}}.}
A única diferença é que o sinal de um propagador está errado no caso Lorentz: o componente temporal tem um propagador de sinal oposto. Isso significa que esses estados de partícula têm norma negativa - eles não são estados físicos. No caso dos fótons, é fácil mostrar por métodos de diagrama que esses estados não são físicos – sua contribuição cancela com fótons longitudinais para deixar apenas duas contribuições físicas de polarização de fótons para qualquer valor de k.
Se a média sobre f é feito com um coeficiente diferente de 1/2, os dois termos não cancelam completamente. Isso dá um Lagrangian covariante com um coeficiente λ λ - Sim., que não afeta nada:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 12(∂ ∂ μ μ AProcesso Processo ∂ ∂ μ μ AProcesso Processo - Sim. - Sim. λ λ (∂ ∂ μ μ Aμ μ )2){displaystyle S=int {tfrac {1}{2}}left(partial ^{mu }A^{nu }partial _{mu }A_{nu }-lambda left(partial _{mu }A^{mu }right)^{2}right)}
e o propagador covariante para QED é:
- ⟨Aμ μ (k)AProcesso Processo (k?))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ (k+k?)gμ μ Processo Processo - Sim. - Sim. λ λ kμ μ kProcesso Processo k2k2.{displaystyle leftlangle A_{mu }(k)A_{nu }(k')rightrangle =delta left(k+k'right){frac {g_{mu nu }-lambda Não. Não. ? }}{k^{2}}{k^{2}}}}}}.}
Gira 1: fantasmas não abelianos
Para encontrar as regras de Feynman para campos de gauge não abelianos, o procedimento que realiza a fixação do gauge deve ser cuidadosamente corrigido para levar em conta uma mudança de variáveis na integral de caminho.
O fator de fixação do medidor tem um determinante extra ao exibir a função delta:
- δ δ (∂ ∂ μ μ Aμ μ - Sim. - Sim. f)e- Sim. - Sim. f22- Não.M{displaystyle delta left(partial _{mu }A_{mu }-fright)e^{-{frac {f^{2}}{2}}}det M.
Para encontrar a forma do determinante, considere primeiro uma integral bidimensional simples de uma função f que depende apenas de r, não no ângulo θ. Inserindo uma integral sobre θ:
- ∫ ∫ f(R)DxDSim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ f(R)∫ ∫ Dθ θ δ δ (Sim.)|DSim.Dθ θ |DxDSim.{displaystyle int f(r),dx,dy=int f(r)int dtheta ,delta (y)left|{frac {dy}{dtheta }}right|,dx,dy}
O fator derivado garante que o pop-up da função delta em θ remova a integral. Trocando a ordem de integração,
- ∫ ∫ f(R)DxDSim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ Dθ θ ∫ ∫ f(R)δ δ (Sim.)|DSim.Dθ θ |DxDSim.{displaystyle int f(r),dx,dy=int dtheta ,int f(r)delta (y)left|{frac {dy}{dtheta }}right|,dx,dy}
mas agora a função delta pode ser exibida em y,
- ∫ ∫ f(R)DxDSim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ Dθ θ 0∫ ∫ f(x)|DSim.Dθ θ |Dx.{displaystyle int f(r),dx,dy=int dtheta _{0},int f(x)left|{frac {dy}{dtheta }}right|,dx,}
A integral sobre θ fornece apenas um fator geral de 2π, enquanto a taxa de mudança de y com uma mudança em θ é apenas x, então este exercício reproduz a fórmula padrão para integração polar de uma função radial:
- ∫ ∫ f(R)DxDSim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2D D ∫ ∫ f(x)xDx{displaystyle int f(r),dx,dy=2pi int f(x)x,dx}
Na integral de caminho para um campo de calibre não abeliano, a manipulação análoga é:
- ∫ ∫ DA∫ ∫ δ δ (F(A))- Não.(∂ ∂ F∂ ∂ G)DGeEu...S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ DG∫ ∫ δ δ (F(A))- Não.(∂ ∂ F∂ ∂ G)eEu...S{displaystyle int DAint delta {big (}F(A){big)}det left({frac {partial F}{partial G}}right),DGe^{iS}=int DGint delta {big (}F(A){big)}det left({frac {partial F}{partial G}}right}
O fator na frente é o volume do grupo de medidores e contribui com uma constante, que pode ser descartada. A integral restante está sobre a ação fixa do medidor.
- ∫ ∫ - Não.(∂ ∂ F∂ ∂ G)eEu...SGFDA{displaystyle int det left({frac {partial F}{partial G}}right)e^{iS_{GF}},DA,}
Para obter um medidor covariante, a condição de fixação do medidor é a mesma do caso Abeliano:
- ∂ ∂ μ μ Aμ μ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =f,{displaystyle partial _{mu }A^{mu }=f,}
Cuja variação sob uma transformação de gauge infinitesimal é dada por:
- ∂ ∂ μ μ Dμ μ α α ,{displaystyle partial _{mu },D_{mu }alpha ,}
onde α é o elemento de valor adjunto da álgebra de Lie em cada ponto que executa a transformação de calibre infinitesimal. Isso adiciona o determinante Faddeev Popov à ação:
- - Não.(∂ ∂ μ μ Dμ μ ){displaystyle det left(partial _{mu },D_{mu }right),}
que pode ser reescrito como uma integral de Grassmann introduzindo campos fantasmas:
- ∫ ∫ e? ? ? ? ∂ ∂ μ μ Dμ μ ? ? D? ? ? ? D? ? {displaystyle int e^{{bar {eta }}partial _{mu },D^{mu }eta },D{bar {eta }},Deta ,}
O determinante é independente de f, então o caminho integral sobre f pode fornecer o propagador de Feynman (ou um propagador covariante) escolhendo a medida para f como no caso abeliano. A ação fixa do medidor completo é então a ação Yang Mills no medidor Feynman com uma ação fantasma adicional:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ T. ∂ ∂ μ μ AProcesso Processo ∂ ∂ μ μ AProcesso Processo +fJJkEu...∂ ∂ Processo Processo AEu...μ μ Aμ μ JJAProcesso Processo k+fJJREu...fkEu...RAEu...AJJAkAEu...+T. ∂ ∂ μ μ ? ? ? ? ∂ ∂ μ μ ? ? +? ? ? ? AJJ? ? Não. S=int operatorname {Tr} partial _{mu }A_{nu }partial ^{mu }A^{nu }+f_{jk}^{i}partial ^{nu }A_{i}^{mu }A_{mu }^{j}A_{nu }^{k}+f_{jr}^{i}f_{kl}^{r}A_{i}A_{j}A^{k}A^{l}+operatorname {Tr} partial _{mu }{bar {eta }}partial ^{mu }eta +{bar {eta} }}A_{j}eta ,}
Os diagramas são derivados desta ação. O propagador para os campos de spin-1 tem a forma usual de Feynman. Existem vértices de grau 3 com fatores de momento cujos acoplamentos são as constantes de estrutura, e vértices de grau 4 cujos acoplamentos são produtos de constantes de estrutura. Existem loops fantasmas adicionais, que cancelam estados longitudinais e semelhantes ao tempo em loops A.
No caso Abeliano, o determinante para calibres covariantes não depende de A, então os fantasmas não contribuem para o diagramas conectados.
Representação de caminho de partícula
Os diagramas de Feynman foram originalmente descobertos por Feynman, por tentativa e erro, como uma forma de representar a contribuição para a matriz S de diferentes classes de trajetórias de partículas.
Representação de Schwinger
O propagador escalar euclidiano tem uma representação sugestiva:
- 1p2+m2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 0∞ ∞ e- Sim. - Sim. ? ? (p2+m2)D? ? Não. {1}{p^{2}+m^{2}}}=int _{0}^{infty }e^{-tau left(p^{2}+m^{2}right)},dtau }
O significado dessa identidade (que é uma integração elementar) é esclarecido pela transformação de Fourier para o espaço real.
- ? ? (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 0∞ ∞ D? ? e- Sim. - Sim. m2? ? 1(4D D ? ? )D/2e- Sim. - Sim. x24? ? {displaystyle Delta (x)=int _{0}^{infty }dtau e^{-m^{2}tau }{frac {1}{({4pi tau })^{d/2}}}e^{frac {-x^{2}}{4tau }}}
A contribuição em qualquer valor de τ para o propagador é um gaussiano de largura √τ. A função de propagação total de 0 a x é uma soma ponderada de todos os tempos adequados τ de um gaussiano normalizado, a probabilidade de terminar em x após um caminhada aleatória de tempo τ.
A representação do caminho integral para o propagador é então:
- ? ? (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 0∞ ∞ D? ? ∫ ∫ DXe- Sim. - Sim. ∫ ∫ 0? ? (x:: 22+m2)D? ? ?{displaystyle Delta (x)=int _{0}^{infty }dtau int DX,e^{-int limits _{0}^{tau }left({frac {{dot {x}}^{2}}{2}}+m^{2}right)dtau '
que é uma reescrita de caminho integral da representação de Schwinger.
A representação de Schwinger é útil para tornar manifesto o aspecto de partícula do propagador e para denominadores de simetria de diagramas de loop.
Combinando denominadores
A representação de Schwinger tem uma aplicação prática imediata para diagramas de loop. Por exemplo, para o diagrama na teoria φ4 formado pela união de dois estilos xs juntos em duas meias linhas, e tornando as linhas restantes externas, a integral sobre os propagadores internos no loop é:
- ∫ ∫ k1k2+m21(k+p)2+m2.{displaystyle int _{k}{frac {1}{k^{2}+m^{2}}}{frac {1}{(k+p)^{2}+m^{2}}},.}
Aqui uma linha carrega o momento k e a outra k + p. A assimetria pode ser corrigida colocando tudo na representação de Schwinger.
- ∫ ∫ ),)?e- Sim. - Sim. )(k2+m2)- Sim. - Sim. )?((k+p)2+m2)D)D)?.{displaystyle int _{t,t'}e^{-t(k^{2}+m^{2})-t'left((k+p)^{2}+m^{2}right)},dt,dt',.}
Agora o expoente depende principalmente de t + t′,
- ∫ ∫ ),)?e- Sim. - Sim. ()+)?)(k2+m2)- Sim. - Sim. )?2p)) k- Sim. - Sim. )?p2,{displaystyle int _{t,t'}e^{-(t+t')(k^{2}+m^{2})-t'2pcdot k-t'p^{2}},}
exceto pela pequena parte assimétrica. Definindo a variável u = t + t′ e v = t′/u, a variável estilo u vai de 0 a ∞, enquanto v vai de 0 a 1. A variável u é o tempo total adequado para o loop, enquanto v parametriza a fração do tempo adequado na parte superior do loop versus a parte inferior.
O jacobiano para esta transformação de variáveis é fácil de calcular a partir das identidades:
- D(uv)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D)?Du= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D)+D)?,{displaystyle d(uv)=dt'quad du=dt+dt',}
e "cunhamento" dá
- uDu∧ ∧ Dv= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D)∧ ∧ D)?{displaystyle u,duwedge dv=dtwedge dt',}.
Isso permite que a integral u seja avaliada explicitamente:
- ∫ ∫ u,vue- Sim. - Sim. u(k2+m2+v2p)) k+vp2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 1(k2+m2+v2p)) k- Sim. - Sim. vp2)2Dv{displaystyle int _{u,v}ue^{-uleft(k^{2}+m^{2}+v2pcdot k+vp^{2}right)}=int {frac {1}{left(k^{2}+m^{2}+v2pcdot k-vp^{2}right)^{2}}},dv}
deixando apenas o v-integral. Este método, inventado por Schwinger, mas geralmente atribuído a Feynman, é chamado de denominador de combinação. Abstratamente, é a identidade elementar:
- 1AB= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 011(vA+(1- Sim. - Sim. v)B)2Dv{displaystyle {frac {1}{AB}}=int _{0}^{1}{frac {1}{{big (}vA+(1-v)B{big)}^{2}}},dv}
Mas esta forma não fornece a motivação física para introduzir v; v é a proporção de tempo adequado em uma das pernas do loop.
Uma vez que os denominadores são combinados, uma mudança em k para k′ = k + vp simetria tudo:
- ∫ ∫ 01∫ ∫ 1(k2+m2+2vp)) k+vp2)2DkDv= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 01∫ ∫ 1(k?2+m2+v(1- Sim. - Sim. v)p2)2Dk?Dv{displaystyle int _{0}^{1}int (k^{2}+m^{2}+2vpcdot k+vp^{2}right)^{2}}},dk,dv=int _{0}^{1}int {frac {1}{left(k'^{2}+m^{2}+v(1-v)p^{2}right)^{2}}},dk',dv}
Esta forma mostra que o momento em que p2 é mais negativo que quatro vezes a massa da partícula em o loop, que ocorre em uma região física do espaço de Lorentz, a integral tem um corte. É exatamente quando o momento externo pode criar partículas físicas.
Quando o loop tem mais vértices, há mais denominadores para combinar:
- ∫ ∫ Dk1k2+m21(k+p1)2+m2⋯ ⋯ 1(k+pn)2+m2{displaystyle int dk,{frac {1}{k^{2}+m^{2}}}{frac {1}{(k+p_{1})^{2}+m^{2}}}cdots {frac {1}{(k+p_{n})^{2}+m^{2}}}}
A regra geral segue a prescrição de Schwinger para n + 1 denominadores:
- 1D0D1⋯ ⋯ Dn= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 0∞ ∞ ⋯ ⋯ ∫ ∫ 0∞ ∞ e- Sim. - Sim. u0D0⋯ ⋯ - Sim. - Sim. unDnDu0⋯ ⋯ Dun.Não. {1}{D_{0}D_{1}cdots D_{n}}}=int _{0}^{infty }cdots int _{0}^{infty }e^{-u_{0}D_{0}cdots -u_{n}D_{n}},du_{0}cdots du_{n},.}
A integral sobre os parâmetros de Schwinger ui pode ser dividida como antes em uma integral sobre o tempo adequado total u = u0 + u 1... + un e uma integral sobre a fração do tempo adequado em todos, exceto no primeiro segmento do loop vi = ui/u para i ∈ {1,2,...,n}. Os vi são positivos e somam menos que 1, de modo que v integral está acima de uma n-dimensional simples.
O jacobiano para a transformação de coordenadas pode ser calculado como antes:
- Du= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Du0+Du1⋯ ⋯ +DunNão. du=du_{0}+du_{1}cdots +du_{n},}
- D(uvEu...)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =DuEu....{displaystyle d(uv_{i})=du_{i},.}
Juntando todas essas equações, obtém-se
- unDu∧ ∧ Dv1∧ ∧ Dv2⋯ ⋯ ∧ ∧ Dvn= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Du0∧ ∧ Du1⋯ ⋯ ∧ ∧ Dun.{displaystyle u^{n},duwedge dv_{1}wedge dv_{2}cdots wedge dv_{n}=du_{0}wedge du_{1}cdots wedge du_{n},.}
Isso dá a integral:
- ∫ ∫ 0∞ ∞ ∫ ∫ SEu...mpEu...exune- Sim. - Sim. u(v0D0+v1D1+v2D2⋯ ⋯ +vnDn)Dv1⋯ ⋯ DvnDu,{displaystyle int _{0}^{infty }int _{mathrm {simplex} }u^{n}e^{-uleft(v_{0}D_{0}+v_{1}D_{1}+v_{2}D_{2}cdots +v_{n}D_{n}right)},dv_{1}cdots dv_{n},du,}
onde o simplex é a região definida pelas condições
- 0quad {mbox{and}}quad sum _{i=1}^{n}v_{i}vEu...>0eGerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nvEu...<1Não. v_{i}>0quad {mbox{and}}quad sum _{i=1}^{n}v_{i}<1}
0quad {mbox{and}}quad sum _{i=1}^{n}v_{i}
bem como
- v0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. - Sim. Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nvEu....Não. v_{0}=1-sum _{i=1}^{n}v_{i},.}
Realizar a integral u fornece a receita geral para combinar denominadores:
- 1D0⋯ ⋯ Dn= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =n!∫ ∫ SEu...mpEu...ex1(v0D0+v1D1⋯ ⋯ +vnDn)n+1Dv1Dv2⋯ ⋯ Dvn{displaystyle {frac {1}{D_{0}cdots D_{n}}}=n!int _{mathrm {simplex}{frac {1}{left (v_{0}D_{0}+v_{1}D_{1}cdots +v_{n}D_{n}right)^{n+1}}},dv_{1},dv_{2}cdots Dv_{n}}
Como o numerador do integrando não está envolvido, a mesma prescrição funciona para qualquer loop, independentemente dos spins carregados pelas pernas. A interpretação dos parâmetros vi é que eles são a fração do tempo total apropriado gasto em cada perna.
Dispersão
As funções de correlação de uma teoria quântica de campos descrevem a dispersão de partículas. A definição de "partícula" na teoria de campos relativísticos não é auto-evidente, porque se você tentar determinar a posição de modo que a incerteza seja menor que o comprimento de onda compton, a incerteza na energia é grande o suficiente para produzir mais partículas e antipartículas do mesmo tipo a partir do vácuo. Isso significa que a noção de um estado de partícula única é até certo ponto incompatível com a noção de um objeto localizado no espaço.
Na década de 1930, Wigner deu uma definição matemática para os estados de partícula única: eles são uma coleção de estados que formam uma representação irredutível do grupo de Poincaré. Os estados de partícula única descrevem um objeto com uma massa finita, um momento bem definido e um spin. Essa definição é adequada para prótons e nêutrons, elétrons e fótons, mas exclui quarks, que estão permanentemente confinados, de modo que o ponto de vista moderno é mais complacente: uma partícula é qualquer coisa cuja interação pode ser descrita em termos de diagramas de Feynman, que têm uma interpretação como uma soma sobre as trajetórias das partículas.
Um operador de campo pode agir para produzir um estado de uma partícula a partir do vácuo, o que significa que o operador de campo φ(x) produz uma superposição de estados de partículas de Wigner. Na teoria do campo livre, o campo produz apenas um estado de partícula. Mas quando há interações, o operador de campo também pode produzir estados de 3 partículas, 5 partículas (se não houver simetria +/− também 2, 4, 6 partículas). Calcular a amplitude de espalhamento para estados de partícula única requer apenas um limite cuidadoso, enviando os campos para o infinito e integrando no espaço para se livrar das correções de ordem superior.
A relação entre funções de dispersão e correlação é o teorema LSZ: A amplitude de dispersão para n partículas para ir para m partículas em um evento de dispersão é dado pela soma dos diagramas de Feynman que entram na função de correlação para n + m inserções de campo, deixando de fora os propagadores para as pernas externas.
Por exemplo, para a interação λφ4 da seção anterior, a ordem λ contribuição para a função de correlação (Lorentz) é:
- ⟨φ φ (k1)φ φ (k2)φ φ (k3)φ φ (k4))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...k12Eu...k22Eu...k32Eu...k42Eu...λ λ {displaystyle leftlangle phi (k_{1})phi (k_{2})phi (k_{3})phi (k_{4})rightrangle ={frac {i}{k_{1}^{2}}}{frac {i}{k_{2}^{2}}}{frac {i}{k_{3}^{2}}}{frac {i}{k_{4}^{2}}}ilambda ,}
Remover os propagadores externos, ou seja, remover os fatores de i /k2, fornece a amplitude de dispersão invariante M:
- M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...λ λ {displaystyle M=ilambda ,}
que é uma constante, independente do momento de entrada e saída. A interpretação da amplitude de dispersão é que a soma de |M |2 sobre todos os estados finais possíveis é a probabilidade do evento de dispersão. A normalização dos estados de partícula única deve ser escolhida com cuidado, no entanto, para garantir que M seja uma invariante relativística.
Estados de partícula única não relativísticos são rotulados pelo momento k e são escolhidos para ter a mesma norma em todos os valor de k. Isso ocorre porque o operador de unidade não relativístico em estados de partícula única é:
- ∫ ∫ Dk|k)) ⟨ ⟨ k|.{displaystyle int dk,|krangle langle k|,.}
Na relatividade, a integral sobre os k-estados para uma partícula de massa m integra sobre uma hipérbole em E,k espaço definido pela relação energia-momento:
- E2- Sim. - Sim. k2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =m2.Não. E^{2}-k^{2}=m^{2},.}
Se a integral pesar cada k ponto igualmente, a medida não é invariante de Lorentz. A medida invariante integra todos os valores de k e E, restringindo à hipérbole com uma função delta invariante de Lorentz:
- ∫ ∫ δ δ (E2- Sim. - Sim. k2- Sim. - Sim. m2)|E,k)) ⟨ ⟨ E,k|DEDk= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ Dk2E|k)) ⟨ ⟨ k|.{displaystyle int delta (E^{2}-k^{2}-m^{2})|E,krangle langle E... k|,dE,dk=int {dk over 2E}|krangle langle k|,.}
Portanto, os estados k normalizados são diferentes dos k-estados por um fator de
- E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(k2- Sim. - Sim. m2)14.{displaystyle {sqrt {E}}=left(k^{2}-m^{2}right)^{frac {1}{4}},.}
A amplitude invariante M é então a amplitude de probabilidade para estados de entrada relativisticamente normalizados se tornarem estados de saída relativisticamente normalizados.
Para valores não relativísticos de k, a normalização relativística é a mesma que a normalização não relativística (até um fator constante √m). Neste limite, a amplitude de dispersão invariante φ4 ainda é constante. As partículas criadas pelo campo φ se espalham em todas as direções com igual amplitude.
O potencial não relativístico, que se espalha em todas as direções com uma amplitude igual (na aproximação de Born), é aquele cuja transformada de Fourier é constante - um potencial de função delta. A dispersão de ordem mais baixa da teoria revela a interpretação não relativística dessa teoria - ela descreve uma coleção de partículas com uma repulsão de função delta. Duas dessas partículas têm aversão a ocupar o mesmo ponto ao mesmo tempo.
Efeitos não perturbativos
Pensando nos diagramas de Feynman como uma série de perturbações, efeitos não perturbativos como tunelamento não aparecem, porque qualquer efeito que vai a zero mais rápido do que qualquer polinômio não afeta a série de Taylor. Mesmo os estados ligados estão ausentes, uma vez que em qualquer ordem finita as partículas são trocadas apenas um número finito de vezes, e para fazer um estado ligado, a força de ligação deve durar para sempre.
Mas esse ponto de vista é enganoso, porque os diagramas não apenas descrevem o espalhamento, mas também são uma representação das correlações da teoria de campos de curta distância. Eles codificam não apenas processos assintóticos como espalhamento de partículas, mas também descrevem as regras de multiplicação para campos, a expansão do produto operador. Os processos de tunelamento não perturbativo envolvem configurações de campo que, em média, aumentam quando a constante de acoplamento diminui, mas cada configuração é uma superposição coerente de partículas cujas interações locais são descritas pelos diagramas de Feynman. Quando o acoplamento é pequeno, estes se tornam processos coletivos que envolvem grande número de partículas, mas onde as interações entre cada uma das partículas são simples. (A série de perturbações de qualquer teoria quântica de campos interativos tem raio zero de convergência, complicando o limite da série infinita de diagramas necessários (no limite do acoplamento nulo) para descrever tais configurações de campo.)
Isso significa que efeitos não perturbativos aparecem assintoticamente em resumos de classes infinitas de diagramas, e esses diagramas podem ser localmente simples. Os gráficos determinam as equações locais de movimento, enquanto as configurações permitidas em larga escala descrevem a física não perturbativa. Mas como os propagadores de Feynman não são locais no tempo, traduzir um processo de campo para uma linguagem de partícula coerente não é completamente intuitivo e só foi explicitamente trabalhado em certos casos especiais. No caso de estados vinculados não relativísticos, a equação de Bethe-Salpeter descreve a classe de diagramas a incluir para descrever um átomo relativístico. Para a cromodinâmica quântica, as regras de soma de Shifman–Vainshtein–Zakharov descrevem modos de campo de comprimento de onda longo não perturbativamente excitados em linguagem de partículas, mas apenas de maneira fenomenológica.
O número de diagramas de Feynman em altas ordens de teoria de perturbação é muito grande, porque existem tantos diagramas quanto grafos com um determinado número de nós. Efeitos não perturbativos deixam uma marca na forma como o número de diagramas e resumos divergem em alta ordem. É apenas porque os efeitos não perturbativos aparecem de forma oculta nos diagramas que foi possível analisar os efeitos não perturbativos na teoria das cordas, onde em muitos casos uma descrição de Feynman é a única disponível.
Na cultura popular
- O uso do diagrama acima da partícula virtual produzindo um par quark-antiquark foi destaque na televisão sit-com O Big Bang Teoria, no episódio "The Bat Jar Conjecture".
- Histórias de Doutoramento de 11 de janeiro de 2012, mostra diagramas de Feynman que visualizar e descrever interações acadêmicas quânticas, ou seja, os caminhos seguidos por estudantes de doutorado ao interagir com seus conselheiros.
- Diagramas de vácuo uma história de ficção científica de Stephen Baxter apresenta o diagrama de vácuo titular, um tipo específico de diagrama de Feynman.
- Feynman e sua esposa, Gweneth Howarth, compraram um Dodge Tradesman Maxivan em 1975, e o tinham pintado com diagramas de Feynman.
Fontes
- Hooft, Gerardus; Veltman, Martinus (1973). "Diagrammar". CERN Yellow Report. doi:10.5170/CERN-1973-009.
{{cite journal}}: A revista Cite requer|journal=(ajuda) - Kaiser, David (2005). Desenho Theories Apart: The Dispersion of Feynman Diagrams in Pós-guerra Física. Chicago, IL: University of Chicago Press. ISBN 0-226-42266-6.
- Veltman, Martinus (1994-06-16). Diagrama: O Caminho para os Diagramas de Feynman. Cambridge Lecture Notes in Physics. ISBN 0-521-45692-4. (expanded, updated version of 't Hooft & Veltman, 1973, citado acima)
- Srednicki, Mark (2006). Teoria Quantum Field. Script.
- Schweber, S. S. (1994). QED e os homens que o fizeram: Dyson, Feynman, Schwinger, e Tomonaga. Princeton University Press. ISBN 978-0691033273.
Contenido relacionado
Molécula diatômica
Amperímetro
Dimensão


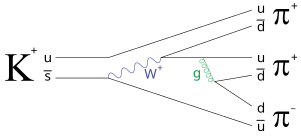
































































![iW[J]equiv ln Z[J].](https://wikimedia.org/api/rest_v1/media/math/render/svg/a03aef8a72b98aa83afeccb54512c30e74dd0762)
![Z[J]propto sum _{k}{D_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c7b6e822c008b3a97c2e25ae9a16d806decc9e7)


![{displaystyle Z[J]propto prod _{i}{sum _{n_{i}=0}^{infty }{frac {C_{i}^{n_{i}}}{n_{i}!}}}=exp {sum _{i}{C_{i}}}propto exp {W[J]},.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50886f901a854ec595c3b9727199e105ad57b73f)




![{displaystyle log {big (}Z[h]{big)}=sum _{n,C}h(k_{1})h(k_{2})cdots h(k_{n})C(k_{1},cdotsk_{n}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bb5547d19ab5fdb64ff700ecc8e3835311e446c)
![{displaystyle Z[h]=int e^{iS+iint hphi },Dphi ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7ea2bd0c5073e68ceff5ddba15e555ce70f92a6)

![{displaystyle Z[h]=int e^{iS}e^{iint _{x}h(x)phi (x)},Dphi =leftlangle e^{ihphi }rightrangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b66d7bcdfcff36ef81756bc3cda53721bd81d685)



![{displaystyle leftlangle phi (x)rightrangle ={frac {1}{Z}}{frac {partial }{partial h(x)}}Z[h]={frac {partial }{partial h(x)}}log {big (}Z[h]{big)},.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/370ee6c83d4c8ed003752105106c84371401dfa1)






















































