Densidade
Densidade (densidade de massa volumétrica ou massa específica) é a massa da substância por unidade de volume. O símbolo mais usado para densidade é ρ (a letra minúscula grega rho), embora a letra latina D também possa ser usada. Matematicamente, a densidade é definida como massa dividida por volume:
- ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mV{displaystyle rho ={frac Não.
onde ρ é a densidade, m é a massa e V é o volume. Em alguns casos (por exemplo, na indústria de petróleo e gás dos Estados Unidos), a densidade é vagamente definida como seu peso por unidade de volume, embora isso seja cientificamente impreciso – essa quantidade é mais especificamente chamada de peso específico.
Para uma substância pura, a densidade tem o mesmo valor numérico que sua concentração de massa. Materiais diferentes geralmente têm densidades diferentes, e a densidade pode ser relevante para flutuabilidade, pureza e embalagem. Ósmio e irídio são os elementos mais densos conhecidos em condições padrão de temperatura e pressão.
Para simplificar as comparações de densidade em diferentes sistemas de unidades, às vezes ela é substituída pela quantidade adimensional "densidade relativa" ou "gravidade específica", ou seja, a relação entre a densidade do material e a de um material padrão, geralmente água. Assim, uma densidade relativa inferior a um em relação à água significa que a substância flutua na água.
A densidade de um material varia com a temperatura e a pressão. Esta variação é tipicamente pequena para sólidos e líquidos, mas muito maior para gases. Aumentar a pressão sobre um objeto diminui o volume do objeto e, portanto, aumenta sua densidade. Aumentar a temperatura de uma substância (com algumas exceções) diminui sua densidade aumentando seu volume. Na maioria dos materiais, o aquecimento do fundo de um fluido resulta na convecção do calor do fundo para o topo, devido à diminuição da densidade do fluido aquecido, que faz com que ele suba em relação ao material não aquecido mais denso.
O recíproco da densidade de uma substância é ocasionalmente chamado de volume específico, um termo às vezes usado em termodinâmica. A densidade é uma propriedade intensiva em que aumentar a quantidade de uma substância não aumenta sua densidade; em vez disso, aumenta sua massa.
Outras quantidades ou proporções conceitualmente comparáveis incluem densidade específica, densidade relativa (gravidade específica) e peso específico.
História
Em uma história bem conhecida, mas provavelmente apócrifa, Arquimedes recebeu a tarefa de determinar se o ourives do rei Hiero estava desviando ouro durante a fabricação de uma coroa de ouro dedicada aos deuses e substituindo-a por outra liga mais barata. Arquimedes sabia que a coroa de forma irregular poderia ser esmagada em um cubo cujo volume poderia ser facilmente calculado e comparado com a massa; mas o rei não aprovou isso. Perplexo, Arquimedes disse ter tomado um banho de imersão e observado pela subida da água ao entrar que ele poderia calcular o volume da coroa de ouro através do deslocamento da água. Após esta descoberta, ele saltou de seu banho e correu nu pelas ruas gritando, "Eureka! Eureka!" (Εύρηκα! Grego "Eu encontrei"). Como resultado, o termo "eureka" entrou na linguagem comum e é usado hoje para indicar um momento de iluminação.
A história apareceu pela primeira vez na forma escrita na obra de Vitrúvio. livros de arquitetura, dois séculos depois de sua suposta ocorrência. Alguns estudiosos duvidaram da precisão dessa história, dizendo, entre outras coisas, que o método exigiria medições precisas que seriam difíceis de fazer na época.
Medição de densidade
Existem várias técnicas e padrões para a medição da densidade de materiais. Tais técnicas incluem o uso de um hidrômetro (um método de flutuabilidade para líquidos), balança hidrostática (um método de flutuabilidade para líquidos e sólidos), método de corpo imerso (um método de flutuabilidade para líquidos), picnômetro (líquidos e sólidos), picnômetro de comparação de ar (sólidos), densitômetro oscilante (líquidos), bem como pour and tap (sólidos). No entanto, cada método ou técnica individual mede diferentes tipos de densidade (por exemplo, densidade aparente, densidade esquelética etc.)
Unidade
Da equação para densidade (ρ = m/V), densidade de massa tem qualquer unidade que seja massa dividida por volume. Como existem muitas unidades de massa e volume cobrindo muitas magnitudes diferentes, há um grande número de unidades de densidade de massa em uso. A unidade SI de quilograma por metro cúbico (kg/m3) e a unidade cgs de grama por centímetro cúbico (g/cm3) são provavelmente as unidades mais usadas para densidade. Um g/cm3 é igual a 1000 kg/m3. Um centímetro cúbico (abreviação cc) é igual a um mililitro. Na indústria, outras unidades maiores ou menores de massa e/ou volume costumam ser mais práticas e podem ser usadas unidades usuais nos Estados Unidos. Veja abaixo uma lista de algumas das unidades de densidade mais comuns.
Materiais homogêneos
A densidade em todos os pontos de um objeto homogêneo é igual à sua massa total dividida pelo seu volume total. A massa é normalmente medida com uma balança ou balança; o volume pode ser medido diretamente (a partir da geometria do objeto) ou pelo deslocamento de um fluido. Para determinar a densidade de um líquido ou de um gás, pode-se usar um hidrômetro, um dosímetro ou um medidor de vazão Coriolis, respectivamente. Da mesma forma, a pesagem hidrostática usa o deslocamento da água devido a um objeto submerso para determinar a densidade do objeto.
Materiais heterogêneos
Se o corpo não é homogêneo, então sua densidade varia entre diferentes regiões do objeto. Nesse caso, a densidade em torno de qualquer local é determinada pelo cálculo da densidade de um pequeno volume em torno desse local. No limite de um volume infinitesimal a densidade de um objeto inhomogeneous em um ponto torna-se: ? ? (R→ → )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Dm/DV{displaystyle rho ({vec {r}})=dm/dV}, onde DVNão. é um volume elementar em posição RNão.. A massa do corpo então pode ser expressa como
- m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ V? ? (R→ → )DV.{displaystyle m=int _{V}rho ({vec {r}},dV.}
Materiais não compactos
Na prática, materiais a granel, como açúcar, areia ou neve, contêm espaços vazios. Muitos materiais existem na natureza como flocos, pellets ou grânulos.
Vazios são regiões que contêm algo diferente do material considerado. Normalmente, o vazio é o ar, mas também pode ser vácuo, líquido, sólido ou um gás diferente ou uma mistura gasosa.
O volume a granel de um material - incluindo a fração de vazio - geralmente é obtido por uma medição simples (por exemplo, com um copo medidor calibrado) ou geometricamente a partir de dimensões conhecidas.
Amassa dividida pelo volume volume determina a densidade aparente. Isso não é a mesma coisa que densidade de massa volumétrica.
Para determinar a densidade de massa volumétrica, deve-se primeiro descontar o volume da fração de vazio. Às vezes, isso pode ser determinado pelo raciocínio geométrico. Para o empacotamento compacto de esferas iguais, a fração não vazia pode ser no máximo cerca de 74%. Também pode ser determinado empiricamente. Alguns materiais a granel, no entanto, como areia, têm uma fração de vazio variável que depende de como o material é agitado ou derramado. Pode ser solto ou compacto, com mais ou menos espaço de ar dependendo do manuseio.
Na prática, a fração de vazio não é necessariamente ar, nem mesmo gasosa. No caso da areia, pode ser água, o que pode ser vantajoso para a medição, pois a fração de vazio da areia saturada em água – uma vez que todas as bolhas de ar são completamente expelidas – é potencialmente mais consistente do que a areia seca medida com um vazio de ar.
No caso de materiais não compactos, deve-se também ter cuidado ao determinar a massa da amostra de material. Se o material estiver sob pressão (geralmente a pressão do ar ambiente na superfície da Terra), a determinação da massa de um peso de amostra medido pode precisar levar em conta os efeitos de flutuabilidade devido à densidade do constituinte vazio, dependendo de como a medição foi conduzido. No caso da areia seca, a areia é tão mais densa que o ar que o efeito de flutuação é comumente negligenciado (menos de uma parte em mil).
A mudança de massa ao deslocar um material vazio com outro, mantendo o volume constante, pode ser usada para estimar a fração de vazio, se a diferença na densidade dos dois materiais vazios for conhecida com segurança.
Mudanças de densidade
Em geral, a densidade pode ser alterada alterando a pressão ou a temperatura. Aumentar a pressão sempre aumenta a densidade de um material. Aumentar a temperatura geralmente diminui a densidade, mas há exceções notáveis a essa generalização. Por exemplo, a densidade da água aumenta entre seu ponto de fusão a 0 °C e 4 °C; comportamento semelhante é observado no silício a baixas temperaturas.
O efeito da pressão e da temperatura nas densidades de líquidos e sólidos é pequeno. A compressibilidade para um líquido ou sólido típico é 10−6 bar−1 (1 bar = 0,1 MPa) e uma expansividade térmica típica é 10−5 K−1. Isso se traduz aproximadamente na necessidade de cerca de dez mil vezes a pressão atmosférica para reduzir o volume de uma substância em um por cento. (Embora as pressões necessárias possam ser cerca de mil vezes menores para solo arenoso e algumas argilas.) Uma expansão de um por cento do volume normalmente requer um aumento de temperatura da ordem de milhares de graus Celsius.
Em contraste, a densidade dos gases é fortemente afetada pela pressão. A densidade de um gás ideal é
- ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =MPRT,{displaystyle rho ={frac {MP}{RT}},}
onde M é a massa molar, P é a pressão, R é a constante universal dos gases e T é a temperatura absoluta. Isso significa que a densidade de um gás ideal pode ser duplicada dobrando a pressão ou reduzindo pela metade a temperatura absoluta.
No caso de expansão térmica volumétrica a pressão constante e pequenos intervalos de temperatura, a dependência da temperatura da densidade é
- ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? T01+α α )) ? ? T,{displaystyle rho ={frac _{T_{0}}}{1+alpha cdot Delta T}},}
Onde? ? ? T0{displaystyle rho _{T_{0}}} é a densidade a uma temperatura de referência, α α - Sim. é o coeficiente de expansão térmica do material em temperaturas próximas T0Não. T_{0}}.
Densidade de soluções
A densidade de uma solução é a soma das concentrações de massa (mássica) dos componentes dessa solução.
Concentração de massa (mássica) de cada componente dado ρi em uma solução soma a densidade da solução,
- ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...? ? Eu....{displaystyle rho =sum _{i}varrho _{i}.
Expresso em função das densidades dos componentes puros da mistura e sua participação em volume, permite a determinação de volumes molares excedentes:
- ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...? ? Eu...VEu...V= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...? ? Eu...φ φ Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...? ? Eu...VEu...Gerenciamento Gerenciamento Eu...VEu...+Gerenciamento Gerenciamento Eu...VEEu...,{displaystyle rho =sum _{i}rho _{i){frac {V_{i}}{V}},=sum _{i}rho _{i}varphi _{i}=sum _{i}rho _{i){frac {V_{i}} _{i}V_{i}+sum _{i}{V^{E}}_{i}}},}
desde que não haja interação entre os componentes.
Conhecendo a relação entre os volumes em excesso e os coeficientes de atividade dos componentes, pode-se determinar os coeficientes de atividade:
- VE? ? Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RT∂ ∂ I γ γ Eu...∂ ∂ P.Não. {overline {V^{E}}}_{i}=RT{frac {displaystyle ln gamma} _{i}}{partial P}}.
Densidades
Vários materiais
- Elementos químicos selecionados estão listados aqui. Para as densidades de todos os elementos químicos, consulte Lista de elementos químicos
| Material | ? (kg/m)3) | Notas |
|---|---|---|
| Hidrogénio | 0,0898 | |
| Hélio | 0,179 | |
| Aerographite | 0,2 | |
| Microplataforma metálica | 0.9. | |
| Aerogel | 1.0. | |
| Ar | 1.2. | A nível do mar |
| Hexafluoreto de tungstênio | 12.4 | Um dos gases mais conhecidos em condições padrão |
| hidrogénio líquido | 70 | Em aprox. −255 °C |
| Esportivo | 75 | Aproxado. |
| Cortiça | 240 | Aproxado. |
| Pinheiro | 373 | |
| Lítio | 535 | Least metal denso |
| Madeira | 700 | Temperado, típico |
| Carvalho | 710 | |
| Potássio | 860 | |
| Gelo | 916.7 | A temperatura < 0 °C |
| Óleo de cozinha | 910–930 | |
| Sódio | 970 | |
| Água (fresco) | 1.000. | A 4 °C, a temperatura da sua densidade máxima |
| Água (sal) | 1,030 | 3% |
| Oxigênio líquido | 1.141 | A aprox. −219 °C |
| Nylon | 1.150 | |
| Plásticos | 1.175 | Aprox.; para polipropileno e PETE/PVC |
| Glicerina | 1.261 | |
| Tetracloroetileno | 1,622 | |
| Areia | 1.600 | Entre 1.600 e 2000 |
| Magnésio | 1,740 | |
| Beryllium | 1,850 | |
| Silício | 2,330 | |
| Concreto de concreto | 2.400 | |
| Vidro | 2.500 | |
| Quartzo | 2600 | |
| Granito | 2.700 | |
| Gneiss | 2.700 | |
| Alumínio | 2.700 | |
| calcário | 2,750 | Compacto |
| Basalt | 3. | |
| Diiodomethane | 3,325 | Líquido à temperatura ambiente |
| Diamante | 3.500 | |
| Titânio de titânio | 4,540 | |
| Selênio | 4.800 | |
| Vanadium | 6,100 | |
| Antimônio | 6,690 | |
| Zinco | 7,000 | |
| Cromo | 7.200 | |
| Tintim | 7.310 | |
| Manganês | 7,325 | Aproxado. |
| Ferro de engomar | 7.870 | |
| Aço leve | 7,850 | |
| Nióbio | 8,570 | |
| Latão | 8,600 | |
| Cádmio | 8,650 | |
| Cobalto | 8,900 | |
| Nickel | 8,900 | |
| Cobre | 8,940 | |
| Bismuto | 9,750 | |
| Molibdênio | 10,220 | |
| Prata | 10.500 | |
| Liderança | 11,340 | |
| Thorium | 11.700 | |
| Rhodium | 12,410 | |
| Mercúrio | 13.546 | |
| Tantalum | 16.600 | |
| Uranium | 18,800 | |
| tungstênio | 19,300 | |
| Ouro | 19,320 | |
| Plutão | 19,840 | |
| Rhenium | 21,020 | |
| Platinum Platinum Platinum | 21.450 | |
| Iridium | 22,420 | |
| Osmium | 22,570 | Elemento natural mais denso na Terra |
Notas:
| ||
Outros
| Entidade | ? (kg/m)3) | Notas |
|---|---|---|
| Meio interestelar | 1.7.×10.- Não. | Com base em 10-5 átomos de hidrogênio por centímetro cúbico |
| Interstellar local Nuvem | 5×10.- 22. | Baseado em 0,3 átomos de hidrogênio por centímetro cúbico |
| Meio interestelar | 1.7.×10.- Não. | Com base em 105 átomos de hidrogênio por centímetro cúbico |
| A Terra | 5,515 | Densidade média. |
| O núcleo interno da Terra | 13.000 | Aprox., como listado na Terra. |
| O núcleo do Sol | 33,000–160,000 | Aproxado. |
| Estrela anã branca | 2.×10.9 | Aproxado. |
| Núcleos atômicos | 2.3.×10.17. | Não depende fortemente do tamanho do núcleo |
| Estrela de Neutron | 1×10.18. |
Água
| Temp. (°C) | Densidade (kg/m3) |
|---|---|
| - Não. | 983.854 |
| -20. | 993.547 |
| - Sim. | 998.117 |
| 0 | 999.8395 |
| 4 | 99,992 |
| 10. | 999.7026 |
| 15 | 999.1026 |
| 20. | 998.2071 |
| 22 | 99,7735 |
| 25 | 99.0479 |
| 30 | 995.6502 |
| 40 | 992. |
| 60 | 983.2 |
| 80 | 97,8 |
| 100. | 958.4 |
Notas:
| |
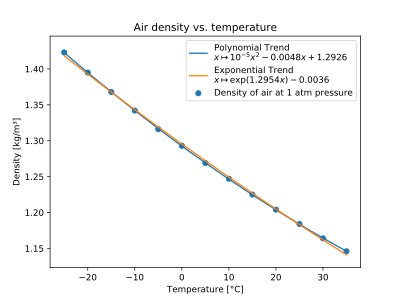
Ar
| T (°C) | ? (kg/m)3) |
|---|---|
| -25 | 1.423 |
| -20. | 1.3.15 |
| - 15. | 1.3.68 |
| - Sim. | 1.342 |
| -5 | 1.3.16 |
| 0 | 1.293 |
| 5 | 1.269 |
| 10. | 1.200 |
| 15 | 1.225 |
| 20. | 1.204 |
| 25 | 1.184 |
| 30 | 1.164 |
| 35 | 1.146 |
Volumes molares de fase líquida e sólida de elementos
Unidades comuns
A unidade SI para densidade é:
- quilograma por metro cúbico (kg/m3)
O litro e a tonelada não fazem parte do SI, mas são aceitáveis para uso com ele, levando às seguintes unidades:
- quilograma por litro (kg/L)
- grama por mililitro (g/mL)
- tonne por metro cúbico (t/m3)
As densidades que usam as seguintes unidades métricas têm todas exatamente o mesmo valor numérico, um milésimo do valor em (kg/m3). A água líquida tem uma densidade de cerca de 1 kg/dm3, tornando qualquer uma dessas unidades SI numericamente conveniente de usar, já que a maioria dos sólidos e líquidos tem densidades entre 0,1 e 20 kg/dm3.
- quilograma por decimetro cúbico (kg/dm3)
- grama por centímetro cúbico (g / cm3)
- 1 g/cm3 = 1000 kg/m3
- megagrama (tonelamento métrico) por metro cúbico (Mg/m)3)
Nas unidades usuais, a densidade pode ser declarada em:
- Onça de avoirdupois por polegada cúbico (1 g/cm3 ≈ 0.578036672 oz/cu in)
- Onça de avoirdupois por onça de líquido (1 g/cm3 ≈ 1.04317556 oz/US fl oz = 1.04317556 lb/US fl pint)
- Avoirdupois libra por polegada cúbico (1 g/cm3 ≈ 0,036127292 lb/cu in)
- libra por pé cúbico (1 g/cm3 ≈ 62.427961 lb/cu ft)
- libra por pátio cúbico (1 g/cm3 ≈ 1685.5549 lb/cu yd)
- libra por galão líquido dos EUA (1 g/cm3 ≈ 8.34540445 lb/US gal)
- libra por bucha americana (1 g/cm3 ≈ 77.6888513 lb/bu)
- lesma por pé cúbico
Unidades imperiais diferentes das anteriores (como o galão imperial e o alqueire diferem das unidades americanas) na prática raramente são usadas, embora encontradas em documentos mais antigos. O galão imperial foi baseado no conceito de que uma onça líquida imperial de água teria uma massa de uma onça Avoirdupois e, na verdade, 1 g/cm3 ≈ 1,00224129 onças por onça líquida imperial = 10,0224129 libras por onça imperial galão. A densidade de metais preciosos poderia ser baseada em onças Troy e libras, uma possível causa de confusão.
Conhecendo o volume da célula unitária de um material cristalino e seu peso de fórmula (em daltons), a densidade pode ser calculada. Um dalton por ångström cúbico é igual a uma densidade de 1,660 539 066 60 g/cm3.
Contenido relacionado
Lise Meitner
Decaimento beta
Deutério