Decaimento beta

β^{- Sim.}
decadência em um núcleo atômico (o antineutrino acompanhante é omitido). O inset mostra a decadência beta de um nêutron livre. Nenhuma dessas representações mostra o virtual intermediário W... Boson.

Na física nuclear, decaimento beta (β-decaimento) é um tipo de decaimento radioativo no qual uma partícula beta (elétron ou pósitron de energia rápida) é emitida de um núcleo atômico, transformando o nuclídeo original a uma isóbara desse nuclídeo. Por exemplo, o decaimento beta de um nêutron o transforma em próton pela emissão de um elétron acompanhado de um antineutrino; ou, inversamente, um próton é convertido em um nêutron pela emissão de um pósitron com um neutrino na chamada emissão de pósitrons. Nem a partícula beta nem seu neutrino (anti-) associado existem dentro do núcleo antes do decaimento beta, mas são criados no processo de decaimento. Por esse processo, os átomos instáveis obtêm uma proporção mais estável de prótons para nêutrons. A probabilidade de um nuclídeo decair devido a beta e outras formas de decaimento é determinada por sua energia de ligação nuclear. As energias de ligação de todos os nuclídeos existentes formam o que é chamado de banda nuclear ou vale de estabilidade. Para que a emissão de elétrons ou pósitrons seja energeticamente possível, a liberação de energia (veja abaixo) ou o valor de Q deve ser positivo.

O decaimento beta é uma consequência da força fraca, que é caracterizada por tempos de decaimento relativamente longos. Os núcleons são compostos de quarks up e quarks down, e a força fraca permite que um quark mude seu sabor pela emissão de um bóson W levando à criação de um par elétron/antineutrino ou pósitron/neutrino. Por exemplo, um nêutron, composto de dois quarks down e um quark up, decai para um próton composto de um quark down e dois quarks up.

A captura eletrônica às vezes é incluída como um tipo de decaimento beta, porque o processo nuclear básico, mediado pela força fraca, é o mesmo. Na captura de elétrons, um elétron atômico interno é capturado por um próton no núcleo, transformando-o em um nêutron, e um neutrino de elétron é liberado.

Descrição

Os dois tipos de decaimento beta são conhecidos como beta menos e beta mais. No decaimento beta menos (β⁻), um nêutron é convertido em um próton, e o processo cria um elétron e um antineutrino de elétron; enquanto no decaimento beta mais (β⁺), um próton é convertido em um nêutron e o processo cria um pósitron e um neutrino de elétron. O decaimento β⁺ também é conhecido como emissão de pósitrons.

O decaimento beta conserva um número quântico conhecido como número leptônico, ou o número de elétrons e seus neutrinos associados (outros léptons são as partículas muon e tau). Essas partículas têm número de léptons +1, enquanto suas antipartículas têm número de léptons -1. Como um próton ou nêutron tem número de lépton zero, o decaimento β⁺ (um pósitron ou antielétron) deve ser acompanhado por um neutrino do elétron, enquanto o decaimento β⁻ (um elétron) deve ser acompanhado por um antineutrino do elétron.

Um exemplo de emissão de elétrons (decaimento β⁻) é o decaimento do carbono-14 em nitrogênio-14 com uma meia-vida de cerca de 5.730 anos:

¹⁴
₆C
→ ¹⁴
₇N
+
e^{- Sim.}
+
Processo
_e

Nesta forma de decaimento, o elemento original torna-se um novo elemento químico em um processo conhecido como transmutação nuclear. Este novo elemento tem um número de massa inalterado A, mas um número atômico Z que é aumentado em um. Como em todos os decaimentos nucleares, o elemento em decaimento (neste caso ¹⁴
₆C
) é conhecido como o nuclídeo pai enquanto o elemento resultante (neste caso ¹⁴
₇N
) é conhecido como o nuclídeo filho.

Outro exemplo é o decaimento do hidrogênio-3 (trítio) em hélio-3 com uma meia-vida de cerca de 12,3 anos:

³
₁H. H. H.
→ ³
₂Ele.
+
e^{- Sim.}
+
Processo
_e

Um exemplo de emissão de pósitrons (decaimento β⁺) é o decaimento do magnésio-23 em sódio-23 com uma meia-vida de cerca de 11,3 s:

²³
₁₂Mg
→ ²³
₁₁Nao
+
e⁺
+
Processo
_e

β⁺ também resulta em transmutação nuclear, com o elemento resultante tendo um número atômico diminuído em um.

Um espectro beta, mostrando uma divisão típica de energia entre elétron e antineutrino

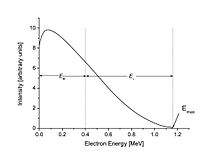
O espectro beta, ou distribuição de valores de energia para as partículas beta, é contínuo. A energia total do processo de decaimento é dividida entre o elétron, o antineutrino e o nuclídeo em recuo. Na figura à direita, é mostrado um exemplo de um elétron com energia de 0,40 MeV do decaimento beta de ²¹⁰Bi. Neste exemplo, a energia de decaimento total é de 1,16 MeV, então o antineutrino tem a energia restante: 1,16MeV − 0,40MeV = 0,76MeV. Um elétron na extrema direita da curva teria a energia cinética máxima possível, deixando a energia do neutrino ser apenas sua pequena massa de repouso.

História

Descoberta e caracterização inicial

A radioatividade foi descoberta em 1896 por Henri Becquerel no urânio e posteriormente observada por Marie e Pierre Curie no tório e nos novos elementos polônio e rádio. Em 1899, Ernest Rutherford separou as emissões radioativas em dois tipos: alfa e beta (agora beta menos), com base na penetração de objetos e na capacidade de causar ionização. Os raios alfa podem ser interrompidos por folhas finas de papel ou alumínio, enquanto os raios beta podem penetrar vários milímetros de alumínio. Em 1900, Paul Villard identificou um tipo de radiação ainda mais penetrante, que Rutherford identificou como um tipo fundamentalmente novo em 1903 e denominou raios gama. Alfa, beta e gama são as três primeiras letras do alfabeto grego.

Em 1900, Becquerel mediu a relação massa-carga (m/e) para partículas beta por o método de J. J. Thomson costumava estudar os raios catódicos e identificar o elétron. Ele descobriu que m/e para uma partícula beta é o mesmo que para o elétron de Thomson e, portanto, sugeriu que a partícula beta é de fato um elétron.

Em 1901, Rutherford e Frederick Soddy mostraram que a radioatividade alfa e beta envolve a transmutação de átomos em átomos de outros elementos químicos. Em 1913, depois que os produtos de mais decaimentos radioativos eram conhecidos, Soddy e Kazimierz Fajans propuseram independentemente sua lei de deslocamento radioativo, que afirma que beta (ou seja,
β⁻
) a emissão de um elemento produz outro elemento uma posição à direita na tabela periódica, enquanto a emissão alfa produz um elemento duas posições à direita esquerda.

Neutrinos

O estudo do decaimento beta forneceu a primeira evidência física da existência do neutrino. Em ambos os decaimentos alfa e gama, a partícula alfa ou gama resultante tem uma distribuição de energia estreita, uma vez que a partícula carrega a energia da diferença entre os estados nucleares inicial e final. No entanto, a distribuição de energia cinética, ou espectro, de partículas beta medida por Lise Meitner e Otto Hahn em 1911 e por Jean Danysz em 1913 mostrou múltiplas linhas em um fundo difuso. Essas medições ofereceram o primeiro indício de que as partículas beta têm um espectro contínuo. Em 1914, James Chadwick usou um espectrômetro magnético com um dos novos contadores de Hans Geiger para fazer medições mais precisas que mostraram que o espectro era contínuo. A distribuição das energias das partículas beta estava em aparente contradição com a lei da conservação da energia. Se o decaimento beta fosse simplesmente a emissão de elétrons como assumido na época, então a energia do elétron emitido deveria ter um valor particular e bem definido. Para o decaimento beta, no entanto, a ampla distribuição observada de energias sugere que a energia é perdida no processo de decaimento beta. Este espectro foi intrigante por muitos anos.

Um segundo problema está relacionado com a conservação do momento angular. Os espectros de banda molecular mostraram que o spin nuclear do nitrogênio-14 é 1 (ou seja, igual à constante de Planck reduzida) e, mais geralmente, que o spin é integral para núcleos de número de massa par e semi-integral para núcleos de número de massa ímpar. Isso foi explicado mais tarde pelo modelo próton-nêutron do núcleo. O decaimento beta deixa o número de massa inalterado, então a mudança do spin nuclear deve ser um número inteiro. No entanto, o spin do elétron é 1/2, portanto, o momento angular não seria conservado se o decaimento beta fosse simplesmente emissão de elétrons.

De 1920 a 1927, Charles Drummond Ellis (junto com Chadwick e colegas) estabeleceu ainda que o espectro de decaimento beta é contínuo. Em 1933, Ellis e Nevill Mott obtiveram fortes evidências de que o espectro beta tem um limite superior efetivo em energia. Niels Bohr havia sugerido que o espectro beta poderia ser explicado se a conservação de energia fosse verdadeira apenas no sentido estatístico, portanto, esse princípio poderia ser violado em qualquer decaimento. No entanto, o limite superior em energias beta determinado por Ellis e Mott descartou essa noção. Agora, o problema de como explicar a variabilidade da energia em produtos de decaimento beta conhecidos, bem como a conservação do momento e do momento angular no processo, tornou-se agudo.

Em uma famosa carta escrita em 1930, Wolfgang Pauli tentou resolver o enigma da energia da partícula beta sugerindo que, além de elétrons e prótons, os núcleos atômicos também continham uma partícula neutra extremamente leve, que ele chamou de nêutron. Ele sugeriu que esse "nêutron" também foi emitido durante o decaimento beta (contabilizando assim a falta de energia, momento e momento angular), mas simplesmente ainda não havia sido observado. Em 1931, Enrico Fermi renomeou Pauli's "neutron" o "neutrino" ('pequeno neutro' em italiano). Em 1933, Fermi publicou sua teoria histórica para o decaimento beta, onde aplicou os princípios da mecânica quântica às partículas da matéria, supondo que elas podem ser criadas e aniquiladas, assim como os quanta de luz nas transições atômicas. Assim, de acordo com Fermi, os neutrinos são criados no processo de decaimento beta, ao invés de contidos no núcleo; o mesmo acontece com os elétrons. A interação do neutrino com a matéria era tão fraca que detectá-la provou ser um grande desafio experimental. Outras evidências indiretas da existência do neutrino foram obtidas observando o recuo dos núcleos que emitiram tal partícula após a absorção de um elétron. Os neutrinos foram finalmente detectados diretamente em 1956 por Clyde Cowan e Frederick Reines no experimento de neutrinos de Cowan-Reines. As propriedades dos neutrinos foram (com algumas pequenas modificações) previstas por Pauli e Fermi.

Β+ decaimento e captura de elétrons

Em 1934, Frédéric e Irène Joliot-Curie bombardearam alumínio com partículas alfa para efetuar a reação nuclear ⁴
₂Ele
+ ²⁷
₁₃Al
→ ³⁰
₁₅P
+ ¹
₀n
, e observou que o isótopo do produto ³⁰
₁₅P
emite um pósitron idênticos aos encontrados nos raios cósmicos (descobertos por Carl David Anderson em 1932). Este foi o primeiro exemplo de
β⁺
decaimento (pósitron emissão), que eles denominaram radioatividade artificial desde ³⁰
15P
é um nuclídeo de vida curta que não existe na natureza. Em reconhecimento à sua descoberta, o casal era umrecebeu o Prêmio Nobel de Química em 1935.

A teoria da captura de elétrons foi discutida pela primeira vez por Gian-Carlo Wick em um artigo de 1934 e depois desenvolvida por Hideki Yukawa e outros. A captura do elétron K foi observada pela primeira vez em 1937 por Luis Alvarez, no nuclídeo ⁴⁸V. Alvarez passou a estudar a captura de elétrons em ⁶⁷Ga e outros nuclídeos.

Não conservação de paridade

Em 1956, Tsung-Dao Lee e Chen Ning Yang notaram que não havia evidência de que a paridade era conservada em interações fracas, e então eles postularam que esta simetria pode não ser preservada pela força fraca. Eles esboçaram o projeto de um experimento para testar a conservação da paridade em laboratório. Mais tarde naquele ano, Chien-Shiung Wu e colegas de trabalho conduziram o experimento Wu mostrando um decaimento beta assimétrico de 60Co em temperaturas frias que provou que a paridade não é conservada no decaimento beta. Esse resultado surpreendente derrubou suposições antigas sobre paridade e força fraca. Em reconhecimento ao seu trabalho teórico, Lee e Yang receberam o Prêmio Nobel de Física em 1957. No entanto, Wu, que era mulher, não recebeu o prêmio Nobel.

Decaimento Β−

O diagrama de Feynman de primeira ordem para
β^{- Sim.}
decadência de um nêutron em um próton, elétron e antineutrino por meio de um bóson W− intermediário. Para diagramas de ordem superior ver

Em
β ⁻
decadência, a interação fraca converte um núcleo atômico em um núcleo com número atômico aumentado em um, enquanto emite um elétron (e−) e um antineutrino de elétron (
ν
_e).
β^-
o decaimento geralmente ocorre em núcleos ricos em nêutrons. A equação genérica é:

^A
_Z.X
→ ^A
_{Z.+ 1}X.
+
e^{- Sim.}
+
Processo
_e

onde A e Z são o número de massa e o número atômico do núcleo em decomposição, e X e X' são os elementos inicial e final, respectivamente.

Outro exemplo é quando o nêutron livre (¹
₀n
) diminui em
β⁻
decai em um próton (
p
):

n
→
p
+
e^{- Sim.}
+
Processo
_e.

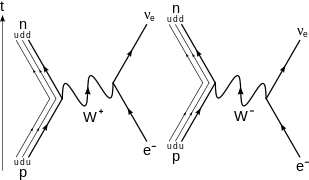
No nível fundamental (conforme representado no diagrama de Feynman à direita), isso é causado pela conversão da carga negativa (−1/3 e) reduz o quark para a carga positiva (+2/3 e) quark up por emissão de um bóson W-; o
W^-
bóson subseqüentemente decai em um elétron e um antineutrino do elétron:

D
→
u
+
e^{- Sim.}
+
Processo
_e.

Β+ decaimento

O diagrama de Feynman de primeira ordem para
β⁺
decadência de um protão em um neutrônio, positrtron e neutrino de elétrons através de um bóson W+ intermediário

Em
β ⁺
decaimento ou emissão de pósitrons, a interação fraca converte um núcleo atômico em um núcleo com número atômico diminuído em um, enquanto emite um pósitron (
e⁺
) e um neutrino de elétron (
ν
_e).
β⁺
decaimento geralmente ocorre em núcleos ricos em prótons. A equação genérica é:

^A
_Z.X
→ ^A
_{Z.- Sim.}X.
+
e⁺
+
Processo
_e

Isso pode ser considerado como o decaimento de um próton dentro do núcleo para um nêutron:

p → n +
e⁺
+
Processo
_e

No entanto,
β⁺
decaimento não pode ocorrer em um próton isolado porque requer energia, devido à massa do nêutron ser maior que a massa do próton.
β⁺
decadência só pode acontecer dentro de núcleos quando a filha núcleo tem uma maior energia de ligação (e, portanto, uma menor energia total) do que o núcleo mãe. A diferença entre essas energias vai para a reação de conversão de um próton em um nêutron, um pósitron e um neutrino e na energia cinética dessas partículas. Esse processo é oposto ao decaimento beta negativo, pois a interação fraca converte um próton em um nêutron, convertendo um quark up em quark down, resultando na emissão de um
W⁺
ou a absorção de um
W⁻
. Quando um
W⁺
bóson é emitido, ele decai em um pósitron e um neutrino do elétron:

u
→
D
+
e⁺
+
Processo
_e.

Captura eletrônica (captura K)

Os diagramas Feynman de primeira ordem para a decadência de captura de elétrons. Um elétron interage com um quark acima no núcleo através de um boson W para criar um quark para baixo e neutrino elétron. Dois diagramas compreendem a ordem principal (segundo), embora como uma partícula virtual, o tipo (e a carga) do W-boson é indistinguível.

Em todos os casos em que
β⁺
decaimento (emissão de pósitrons) de um núcleo é permitida energeticamente, assim também é permitida a captura de elétrons. Este é um processo durante o qual um núcleo captura um de seus elétrons atômicos, resultando na emissão de um neutrino:

^A
_Z.X
+
e^{- Sim.}
→ ^A
_{Z.- Sim.}X.
+
Processo
_e

Um exemplo de captura eletrônica é um dos modos de decaimento do criptônio-81 em bromo-81:

⁸¹
₃₆Kr
+
e^{- Sim.}
→ ⁸¹
₃₅B.
+
Processo
_e

Todos os neutrinos emitidos têm a mesma energia. Em núcleos ricos em prótons onde a diferença de energia entre os estados inicial e final é menor que 2m_ec²,
β⁺
o decaimento não é energeticamente possível e a captura de elétrons é o único modo de decaimento.

Se o elétron capturado vem da camada mais interna do átomo, a camada K, que tem a maior probabilidade de interagir com o núcleo, o processo é chamado de captura K. Se vier do L-shell, o processo é chamado L-capture, etc.

A captura eletrônica é um processo de decaimento competitivo (simultâneo) para todos os núcleos que podem sofrer decaimento β⁺. O inverso, porém, não é verdadeiro: a captura de elétrons é o único tipo de decaimento permitido em nuclídeos ricos em prótons que não possuem energia suficiente para emitir um pósitron e um neutrino.

Transmutação nuclear

Gráfico de isótopos por tipo de decadência nuclear. Nuclídeos alaranjados e azuis são instáveis, com os quadrados pretos entre estas regiões representando nuclídeos estáveis. A linha ininterrupta que passa abaixo de muitos dos nuclides representa a posição teórica no gráfico de nuclides para o qual o número de protão é o mesmo que o número de nêutrons. O gráfico mostra que os elementos com mais de 20 protões devem ter mais nêutrons do que prótons, a fim de ser estável.

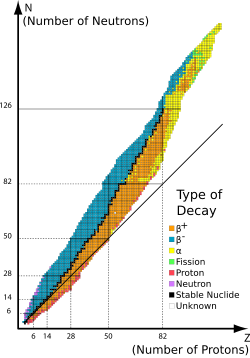
Se o próton e o nêutron fazem parte de um núcleo atômico, os processos de decaimento descritos acima transmutam um elemento químico em outro. Por exemplo:

13755Cs			→	13756 Bando	+	E...	+	Processo	(beta minus deterioração)
2211			→	2210	+	E...	+	Processo	(beta mais decadência)
2211	+	E...	→	2210	+	Processo			(captura eletrônica)

O decaimento beta não altera o número (A) de núcleons no núcleo, mas altera apenas sua carga Z. Assim, o conjunto de todos os nuclídeos com o mesmo A pode ser introduzido; esses nuclídeos isobáricos podem se transformar um no outro via decaimento beta. Para um dado A existe um que é mais estável. Diz-se que é beta estável, porque apresenta um mínimo local do excesso de massa: se tal núcleo tem (A, Z) números, os núcleos vizinhos (A, Z−1) e (A, Z+1) têm maior excesso de massa e podem decair beta em (A, Z), mas não vice-versa. Para todos os números de massa ímpares A, existe apenas uma isóbara estável beta conhecida. Mesmo para A, existem até três diferentes isóbaras beta-estáveis conhecidas experimentalmente; por exemplo, ¹²⁴
₅₀Sn
, ¹²⁴
₅₂Te
e ¹²⁴
₅₄Xe
são todos beta-estáveis. Existem cerca de 350 nuclídeos estáveis em decaimento beta conhecidos.

Competição de tipos de decaimento beta

Normalmente os nuclídeos instáveis são claramente "ricos em nêutrons" ou "rico em prótons", com o primeiro sofrendo decaimento beta e o último sofrendo captura de elétrons (ou mais raramente, devido aos requisitos de energia mais altos, decaimento de pósitrons). No entanto, em alguns casos de radionuclídeos de prótons ímpares e nêutrons ímpares, pode ser energeticamente favorável para o radionuclídeo decair para um isóbaro de prótons pares e nêutrons pares, seja por decaimento beta-positivo ou beta-negativo. Um exemplo frequentemente citado é o isótopo único 6429Cu (29 prótons, 35 nêutrons), que ilustra três tipos de decaimento beta na competição. O cobre-64 tem uma meia-vida de cerca de 12,7 horas. Este isótopo tem um próton desemparelhado e um nêutron desemparelhado, de modo que o próton ou o nêutron podem decair. Este nuclídeo específico (embora não todos os nuclídeos nessa situação) tem quase a mesma probabilidade de decair por meio do decaimento de prótons por emissão de pósitrons ( 18%) ou captura de elétrons (43%) a ⁶⁴
₂₈Ni
, como está decaimento de nêutrons suficiente por emissão de elétrons (39%) para ⁶⁴
₃₀Zn
.

Estabilidade de nuclídeos naturais

A maioria dos nuclídeos que ocorrem naturalmente na Terra são beta estáveis. Os nuclídeos que não são beta estáveis têm meias-vidas que variam de menos de um segundo a períodos de tempo significativamente maiores que a idade do universo. Um exemplo comum de um isótopo de vida longa é o nuclídeo de nêutron ímpar de próton 4019K, que sofre todos os três tipos de decaimento beta (
β^-
,
β⁺
e captura eletrônica) com meia-vida de 1,277×10⁹ anos.

Regras de conservação para decaimento beta

O número de bárions é conservado

B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =nq- Sim. - Sim. nq? ? 3- Sim. (n_{q)-n_{bar {q}}}{3}}}

• nqNão. N_{q}} é o número de quarks constituintes, e
• nq? ? Não. n_{overline {q}} é o número de antiquarks constituintes.

O decaimento beta apenas muda o nêutron para o próton ou, no caso do decaimento beta positivo (captura de elétrons), o próton para o nêutron, de modo que o número de quarks individuais não muda. É apenas o sabor do bárion que muda, aqui rotulado como isospin.

Os quarks para cima e para baixo têm isospin total Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12- Sim. Não. e projeções de isospin

Eu...zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(12para cima quark- Sim. - Sim. 12para baixo quarkNão. I_{text{z}}={begin{cases}{frac {1}{2}}&{text{up quark}}-{frac {1}{2}}&{text{down quark}}end{cases}}}}}

Todos os outros quarks têm I = 0.

Em geral

Eu...zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12(nu- Sim. - Sim. nD){displaystyle I_{text{z}}={frac {1}{2}}(n_{text{u}}-n_{text{d}}) ?

O número de léptons é conservado

L)) nEu... Eu... - Sim. - Sim. nEu... Eu... ? ? Não. Lequiv n. - Não.

portanto, todos os léptons têm atribuído um valor de +1, antiléptons -1 e partículas não leptônicas 0.

n→ → p+e- Sim. - Sim. +Processo Processo ? ? eL:0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0+1- Sim. - Sim. 1{displaystyle {begin{matrix}&{text{n}}&rightarrow &{text{p}}&+&{text{e}}^{-}&+&{bar {nu }}_{text{e}}L:&0&=&0&+&1&-&1end{matrix}}}

Momento angular

Para decaimentos permitidos, o momento angular orbital líquido é zero, portanto, apenas os números quânticos de spin são considerados.

O elétron e o antineutrino são fermions, spin-1/2 objetos, portanto, eles podem acoplar ao total S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1S=1} (paralela) ou S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0- Sim. (anti-paralela).

Para decaimentos proibidos, o momento angular orbital também deve ser levado em consideração.

Liberação de energia

O valor Q é definido como a energia total liberada em um determinado decaimento nuclear. No decaimento beta, Q é, portanto, também a soma das energias cinéticas da partícula beta emitida, do neutrino e do núcleo em recuo. (Devido à grande massa do núcleo em comparação com a da partícula beta e do neutrino, a energia cinética do núcleo em recuo geralmente pode ser negligenciada.) As partículas beta podem, portanto, ser emitidas com qualquer energia cinética variando de 0 a Q. Um Q típico é de cerca de 1 MeV, mas pode variar de alguns keV a algumas dezenas de MeV.

Como a massa restante do elétron é de 511 keV, as partículas beta mais energéticas são ultrarrelativísticas, com velocidades muito próximas da velocidade da luz. No caso do ¹⁸⁷Re, a velocidade máxima da partícula beta é de apenas 9,8% da velocidade da luz.

A tabela a seguir fornece alguns exemplos:

Decaimento Β−

Considere a equação genérica para o decaimento beta

^A
_Z.X
→ ^A
_{Z.+ 1}X.
+
e^{- Sim.}
+
Processo
_e.

O valor Q para este decaimento é

Q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.mN(XZ.A)- Sim. - Sim. mN(XZ.+1A?)- Sim. - Sim. me- Sim. - Sim. mProcesso Processo ? ? e]c2{displaystyle Q=left[m_{N}left({ce {^{mathit {A}}_{mathit {Z}}X}}right)-m_{N}left({ce {^{mathit {A}}_{{mathit {Z}}+1}X'}}right)-m_{e}-m_{{overline {nu }}_{e}}right]c^{2}},

Onde? mN(XZ.A){displaystyle m_{N}left({ce {^{mathit {A}}_{mathit {Z}}X}}right)} é a massa do núcleo do ^A
_Z.X
átomo, me{displaystyle m_{e}} é a massa do elétron, e mProcesso Processo ? ? eNão. M_{{overline (em inglês) }} é a massa do elétron antineutrino. Em outras palavras, a energia total liberada é a energia de massa do núcleo inicial, menos a energia de massa do núcleo final, elétron e antineutrino. A massa do núcleo m_N está relacionado à massa atômica padrão m por

m(XZ.A)c2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mN(XZ.A)c2+Z.mec2- Sim. - Sim. Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Z.BEu....{displaystyle mleft({ce {^{mathit) {A}}_{mathit {Z}}X}}right)c^{2}=m_{N}left({ce {^{mathit {A}}_{mathit {Z}}X}}right)c^{2}+Zm_{e}c^{2}-sum _{i=1}^{Z}B_{i}}.}

elétronB_Eu...mN(XZ.A){displaystyle m_{N}left({ce {^{mathit {A}}_{mathit {Z}}X}}right)}mN(XZ.+1A?)Não. m_{N}left({ce {^{mathit {A}}_{{mathit {Z}}+1}X'}}right)}QZ.

Q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.m(XZ.A)- Sim. - Sim. m(XZ.+1A?)]c2{displaystyle Q=left[mleft({ce {^{mathit {A}}_{mathit {Z}}X}}right)-mleft({ce {^{mathit {A}}_{{mathit {Z}}+1}X'}}right]c^{2}}

Como a reação ocorrerá apenas quando o valor Q é positivo, o decaimento β⁻ pode ocorrem quando a massa do átomo ^A
_ZX
é maior que a massa de átomo ^A
_Z+1X′
.

Β+ decaimento

As equações para decaimento β⁺ são semelhantes, com a equação genérica

^A
_Z.X
→ ^A
_{Z.- Sim.}X.
+
e⁺
+
Processo
_e

dando

Q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.mN(XZ.A)- Sim. - Sim. mN(XZ.- Sim. - Sim. 1A?)- Sim. - Sim. me- Sim. - Sim. mProcesso Processo e]c2.{displaystyle Q=left[m_{N}left({ce {^{mathit {A}}_{mathit {Z}}X}}right)-m_{N}left({ce {^{mathit {A}} {Z}}-1}X'}}right)-m_{e}-m_{nu _{e}}right]c^{2}.}

Q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.m(XZ.A)- Sim. - Sim. m(XZ.- Sim. - Sim. 1A?)- Sim. - Sim. 2me]c2.{displaystyle Q=left[mleft({ce {^{mathit {A}}_{mathit {Z}}X}}right)-mleft({ce {^{mathit {A}} {Z}}-1}X'}}right)-2m_{e}right]c^{2}.}

Como a reação ocorrerá apenas quando o valor Q é positivo, o decaimento β⁺ pode ocorrem quando a massa do átomo ^A
_ZX
excede o de ^A
_Z-1X′
em pelo menos duas vezes a massa do elétron.

Captura de elétrons

O cálculo análogo para captura de elétrons deve levar em conta a energia de ligação dos elétrons. Isso ocorre porque o átomo será deixado em um estado excitado após a captura do elétron, e a energia de ligação do elétron mais interno capturado é significativa. Usando a equação genérica para captura de elétrons

^A
_Z.X
+
e^{- Sim.}
→ ^A
_{Z.- Sim.}X.
+
Processo
_e

nós temos

Q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.mN(XZ.A)+me- Sim. - Sim. mN(XZ.- Sim. - Sim. 1A?)- Sim. - Sim. mProcesso Processo e]c2,{displaystyle Q=left[m_{N}left({ce {^{mathit {A}}_{mathit {Z}}X}}right)+m_{e}-m_{N}left({ce {^{mathit {A}} {Z}}-1}X'}}right)-m_{nu _{e}}right]c^{2},}

Q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.m(XZ.A)- Sim. - Sim. m(XZ.- Sim. - Sim. 1A?)]c2- Sim. - Sim. Bn,{displaystyle Q=left[mleft({ce {^{mathit {A}}_{mathit {Z}}X}}right)-mleft({ce {^{mathit {A}}_{{mathit {Z}}-1}X'}}right]c^{2}-B_{n},}

B_n

Como a energia de ligação do elétron é muito menor que a massa do elétron, os núcleos que podem sofrer decaimento β⁺ sempre podem também sofrer captura de elétrons, mas o inverso não é verdadeiro.

Espectro de emissão beta

Espectro beta de ²¹⁰Bi. E_máx. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Q = 1.16 MeV é a energia máxima

O decaimento beta pode ser considerado como uma perturbação descrita na mecânica quântica e, portanto, a Regra de Ouro de Fermi pode ser aplicada. Isso leva a uma expressão para o espectro de energia cinética N(T) de betas emitidos como segue:

N(T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =CL(T)F(Z.,T)pE(Q- Sim. - Sim. T)2{displaystyle N(T)=C_{L}(T)F(Z,T)pE(Q-T)^{2}}

Onde? T é a energia cinética, C_L é uma função de forma que depende da proibição da decadência (é constante para decaimentos permitidos), F(Z., T) é a função Fermi (veja abaixo) com Z. a carga do núcleo de estado final, E = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = T + Mc² é a energia total, p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(E/c)2- Sim. - Sim. (mc)2(E/c)^{2}-(mc)^{2}} é o impulso, e Q é o valor Q da decadência. A energia cinética do neutrino emitido é dada aproximadamente por Q menos a energia cinética do beta.

Como exemplo, o espectro de decaimento beta de ²¹⁰Bi (originalmente chamado de RaE) é mostrado à direita.

Função Fermi

A função de Fermi que aparece na fórmula do espectro beta dá conta da atração/repulsão coulombiana entre o beta emitido e o núcleo em estado final. Aproximando as funções de onda associadas para serem esfericamente simétricas, a função de Fermi pode ser calculada analiticamente como sendo:

F(Z.,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2(1+S))) (1+2S)2(2p? ? )2S- Sim. - Sim. 2eD D ? ? |)) (S+Eu...? ? )|2,{displaystyle F(Z,T)={frac {2(1+S)}{Gamma (1+2S)^{2}}}(2prho)^{2S-2}e^{pi eta }|Gamma (S+ieta)|^{2},}

Onde? p é o impulso final, Γ a função Gamma, e (se α é a estrutura fina constante e R_N o raio do núcleo de estado final) S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. - Sim. α α 2Z.2{displaystyle S={sqrt {1-alpha ^{2}Z^{2}}, ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =± ± Z.e2c/? ? p{displaystyle eta =pm Ze^{2}c/hbar p}(+ para elétrons, − para positrons) e ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RN/? ? {displaystyle rho =r_{N}/hbar }.

Para betas não relativísticos (Q ≪ m_ec ²), esta expressão pode ser aproximada por:

F(Z.,T)? ? 2D D ? ? 1- Sim. - Sim. e- Sim. - Sim. 2D D ? ? .{displaystyle F(Z,T)approx frac (2pi) }{1-e^{-2pi Sim.

Outras aproximações podem ser encontradas na literatura.

Plano de Kurie

Um gráfico de Kurie (também conhecido como gráfico de Fermi–Kurie) é um gráfico usado no estudo do decaimento beta desenvolvido por Franz N. D. Kurie, no qual a raiz quadrada de o número de partículas beta cujos momentos (ou energia) estão dentro de uma certa faixa estreita, dividido pela função de Fermi, é plotado contra a energia da partícula beta. É uma linha reta para transições permitidas e algumas transições proibidas, de acordo com a teoria do decaimento beta de Fermi. A interceptação do eixo de energia (eixo x) de um gráfico de Kurie corresponde à energia máxima transmitida ao elétron/pósitron (o decaimento Q valor). Com um gráfico de Kurie pode-se encontrar o limite da massa efetiva de um neutrino.

Helicidade (polarização) de neutrinos, elétrons e pósitrons emitidos no decaimento beta

Após a descoberta da não conservação de paridade (ver História), descobriu-se que, no decaimento beta, os elétrons são emitidos principalmente com helicidade negativa, ou seja, eles se movem, ingenuamente falando, como parafusos canhotos cravados em um material (têm polarização longitudinal negativa). Por outro lado, os pósitrons têm principalmente helicidade positiva, ou seja, eles se movem como parafusos destros. Os neutrinos (emitidos no decaimento do pósitron) têm helicidade negativa, enquanto os antineutrinos (emitidos no decaimento do elétron) têm helicidade positiva.

Quanto maior a energia das partículas, maior sua polarização.

Tipos de transições de decaimento beta

Os decaimentos beta podem ser classificados de acordo com o momento angular (valor L) e o spin total (valor S) da radiação emitida. Como o momento angular total deve ser conservado, incluindo o momento angular orbital e de spin, o decaimento beta ocorre por uma variedade de transições de estado quântico para vários momentos angulares nucleares ou estados de spin, conhecidos como "Fermi" ou "Gamow–Teller" transições. Quando as partículas de decaimento beta não possuem momento angular (L = 0), o decaimento é referido como "permitido", caso contrário é "proibido".

Outros modos de decaimento, que são raros, são conhecidos como decaimento de estado ligado e decaimento beta duplo.

Transições de Fermi

A Transição de Fermi é uma decadência beta em que os spins do elétron emitido (positron) e anti-neutrino (neutrino) casal para rotação total S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0- Sim., levando a uma mudança de impulso angular ? ? JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0Não. Delta J=0 entre os estados iniciais e finais do núcleo (assumindo uma transição permitida). No limite não-relativista, a parte nuclear do operador para uma transição Fermi é dada por

OF= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =GVGerenciamento Gerenciamento um? ? ^ ^ um± ± {displaystyle {mathcal {O}}_{F}=G_{V}sum _{a}{hat {tau }}

GVNão. G_{V}}? ? ± ± {displaystyle tau _{pm }}umNão.

Transições Gamow–Teller

A Transição Gamow-Teller é uma decadência beta em que os spins do elétron emitido (positron) e anti-neutrino (neutrino) casal para rotação total S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1S=1}, levando a uma mudança de impulso angular ? ? JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,± ± 1Não. Delta J=0,pm 1} entre os estados iniciais e finais do núcleo (assumindo uma transição permitida). Neste caso, a parte nuclear do operador é dada por

OGT= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =GAGerenciamento Gerenciamento umσ σ ^ ^ um? ? ^ ^ um± ± {displaystyle {mathcal {O}}_{GT}=G_{A}sum _{a}{hat Sim. _{a? }}

GANão. G_{A}}σ σ - Sim.

Transições proibidas

Quando L > 0, o decaimento é referido como "proibido". As regras de seleção nuclear exigem valores altos de L para serem acompanhados por mudanças no spin nuclear (J) e paridade (π). As regras de seleção para as Lésimas transições proibidas são:

? ? JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =L- Sim. - Sim. 1,L,L+1;? ? D D = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(- Sim. - Sim. 1)L,Não. Delta J=L-1,L,L+1;Delta pi =(-1)^{L},}

?D = 1 ou −1JJDL

Proibição	?JJ	?D
Superabaixo	0	Não.
Permitido	0, 1	Não.
Primeiro proibido	0, 1, 2	Sim.
Segundo proibido	1, 2, 3	Não.
Terceiro proibido	2, 3, 4	Sim.

Modos de decaimento raros

Decaimento β- de estado limite

Uma minoria muito pequena de decaimentos de nêutrons livres (cerca de quatro por milhão) são os chamados "decaimentos de dois corpos", nos quais o próton, o elétron e o antineutrino são produzidos, mas o elétron não consegue ganhar a energia de 13,6 eV necessária para escapar do próton e, portanto, simplesmente permanece ligada a ele, como um átomo de hidrogênio neutro. Nesse tipo de decaimento beta, em essência, toda a energia de decaimento do nêutron é transportada pelo antineutrino.

Para átomos totalmente ionizados (núcleos nus), é possível, da mesma forma, que os elétrons não escapem do átomo e sejam emitidos do núcleo para estados atômicos de baixa altitude (orbitais). Isso não pode ocorrer para átomos neutros com estados ligados de baixa altitude que já estão preenchidos por elétrons.

Os decaimentos β do estado ligado foram previstos por Daudel, Jean e Lecoin em 1947, e o fenômeno em átomos totalmente ionizados foi observado pela primeira vez para 163Dy66+ em 1992 por Jung et al. do Centro de Pesquisa de Íons Pesados de Darmstadt. Embora neutro ¹⁶³
Dy é um isótopo estável, o ¹⁶³Dy^{66+ sofre decaimento β nas camadas K e L com uma meia-vida de 47 dias. O núcleo resultante - 163Ho - é estável apenas no estado totalmente ionizado e decairá via captura de elétrons em 163
Dy no estado neutro. A meia-vida para este último é de 4750 anos.}

Outra possibilidade é que um átomo totalmente ionizado sofra um decaimento β muito acelerado, conforme observado para ¹⁸⁷Re por Bosch et al., também em Darmstadt. Neutro ¹⁸⁷Re sofre decaimento β com meia-vida de 41,6×10⁹ anos, mas para ¹⁸⁷re ⁷⁵⁺ isso é reduzido para apenas 32,9 anos. Para comparação, a variação das taxas de decaimento de outros processos nucleares devido ao ambiente químico é inferior a 1%. Devido à diferença de preço de rênio e ósmio e a alta participação de ¹⁸⁷
Re em amostras de rênio encontradas na Terra, isso pode algum dia terá interesse comercial na síntese de metais preciosos.

Duplo declínio beta

Alguns núcleos podem sofrer decaimento beta duplo (decaimento ββ), onde a carga do núcleo muda em duas unidades. O decaimento beta duplo é difícil de estudar, pois o processo tem uma meia-vida extremamente longa. Em núcleos para os quais tanto o decaimento β quanto o decaimento ββ são possíveis, o processo mais raro de decaimento ββ é efetivamente impossível de observar. No entanto, em núcleos onde o decaimento β é proibido, mas o decaimento ββ é permitido, o processo pode ser visto e uma meia-vida medida. Assim, o decaimento ββ geralmente é estudado apenas para núcleos beta estáveis. Assim como o decaimento beta simples, o decaimento beta duplo não altera A; assim, pelo menos um dos nuclídeos com algum dado A deve ser estável em relação ao decaimento beta simples e duplo.

"Comum" o decaimento beta duplo resulta na emissão de dois elétrons e dois antineutrinos. Se os neutrinos forem partículas de Majorana (ou seja, eles são suas próprias antipartículas), ocorrerá um decaimento conhecido como decaimento beta duplo sem neutrinos. A maioria dos físicos de neutrinos acredita que o decaimento beta duplo sem neutrinos nunca foi observado.