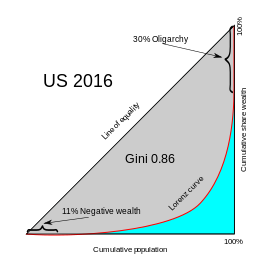
Curva de Lorenz

Uma curva típica de Lorenz

Em economia, a curva de Lorenz é uma representação gráfica da distribuição de renda ou riqueza. Foi desenvolvido por Max O. Lorenz em 1905 para representar a desigualdade na distribuição da riqueza.

A curva é um gráfico que mostra a proporção da renda ou riqueza total assumida pelos x% mais pobres da população, embora isso não seja rigorosamente verdadeiro para uma população finita (veja abaixo). É freqüentemente usado para representar a distribuição de renda, onde mostra para a parte inferior x% dos domicílios, qual porcentagem (y%) da renda total eles têm. A porcentagem de domicílios é plotada no eixo x, a porcentagem de renda no eixo y. Também pode ser usado para mostrar a distribuição de ativos. Nesse uso, muitos economistas o consideram uma medida de desigualdade social.

O conceito é útil para descrever a desigualdade entre o tamanho dos indivíduos em ecologia e em estudos de biodiversidade, onde a proporção cumulativa de espécies é plotada contra a proporção cumulativa de indivíduos. Também é útil na modelagem de negócios: por exemplo, em financiamento ao consumidor, para medir a porcentagem real y% de inadimplência atribuível ao x% de pessoas com piores pontuações de risco.

Explicação

Derivação da curva Lorenz e coeficiente Gini para renda global em 2011

Dados de 2005.

Os pontos na curva de Lorenz representam afirmações como "os 20% mais pobres de todas as famílias têm 10% da renda total"

Uma distribuição de renda perfeitamente igual seria aquela em que todas as pessoas têm a mesma renda. Nesse caso, a N% da base da sociedade sempre teria N% da renda. Isso pode ser representado pela linha reta y = x; chamada de "linha de igualdade perfeita."

Por outro lado, uma distribuição perfeitamente desigual seria aquela em que uma pessoa tem toda a renda e todas as outras não. Nesse caso, a curva seria y = 0% para todos os x < 100%, e y = 100% quando x = 100%. Esta curva é chamada de "linha de desigualdade perfeita."

O coeficiente de Gini é a razão da área entre a linha de perfeita igualdade e a curva de Lorenz observada para a área entre a linha de perfeita igualdade e a linha de perfeita desigualdade. Quanto maior o coeficiente, mais desigual é a distribuição. No diagrama à direita, isso é dado pela razão A/(A+B), onde A e B são as áreas das regiões marcadas no diagrama.

Definição e cálculo

curva de Lorenz para distribuição de riqueza dos EUA em 2016 mostrando riqueza negativa e oligarquia

A curva de Lorenz é um gráfico de probabilidade (um gráfico P–P) comparando a distribuição de uma variável com uma distribuição hipotética uniforme dessa variável. Geralmente pode ser representado por uma função L(F), onde F, a porção cumulativa da população, é representada pelo eixo horizontal, e L, a parcela cumulativa da riqueza ou renda total, é representada pelo eixo vertical.

A curva L não precisa ser uma função crescente suave de F. Para distribuições de riqueza, pode haver oligarquias ou pessoas com riqueza negativa, por exemplo.

Para uma distribuição discreta de Y dada por valores Sim.₁, Sim._n em ordem não crescente (Sim._Eu... ≤ Sim._{Eu...+ 1}) e suas probabilidades f(Sim.JJ)?Pr(Y= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Sim.JJ){displaystyle f(y_{j}):=Pr(Y=y_{j})} a curva Lorenz é a função linear contínua em peça conectando os pontos (F_Eu..., L_Eu...), Eu... = 0 a n, onde F₀ - 0, L₀ = 0, e Eu... = 1 a n:

FEu...?Gerenciamento Gerenciamento JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Eu...f(Sim.JJ)SEu...?Gerenciamento Gerenciamento JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Eu...f(Sim.JJ)Sim.JJLEu...?SEu...Sn{displaystyle {begin{aligned}F_{i}&:=sum _{j=1}^{i}f(y_{j})\S_{i}&:=sum _{j=1}^{i}f(y_{j}),y_{j}\L_{i}&:={frac {S_{i}}{S_{n}}}end{aligned}}}

Quando todos os y_i são igualmente prováveis com probabilidades 1/n, isso simplifica para

FEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...nSEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nGerenciamento Gerenciamento JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Eu...Sim.JJLEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =SEu...Sn{displaystyle {begin{aligned}F_{i}&={frac {i}{n}}\S_{i}&={frac (em inglês) _{j=1}^{i};y_{j}\L_{i}&={frac {S_{i}}{S_{n}}}end{aligned}}}

Para uma distribuição contínua com a função de densidade de probabilidade f e a função de distribuição cumulativa F, a curva de Lorenz L é dada por:

L(F(x))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ - Sim. - Sim. ∞ ∞ x)f())D)∫ ∫ - Sim. - Sim. ∞ ∞ ∞ ∞ )f())D)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ - Sim. - Sim. ∞ ∞ x)f())D)μ μ {displaystyle L(F(x))={frac {int _{-infty }^{x}t,f(t),dt}{int _{-infty }^{infty }t,f(t),dt}}={frac {int _{-infty }^{x}t,f(t),dt}{mu }}}}}}

μ μ - Sim.

Alternativamente, para uma função de distribuição cumulativa F(x) com inverso x(F), o A curva de Lorenz L(F) é dada diretamente por:

L(F)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 0Fx(F1)DF1∫ ∫ 01x(F1)DF1{displaystyle L(F)={frac {int _{0}^{F}x(F_{1}),dF_{1}}{int _{0}^{1}x(F_{1}),dF_{1}}}}

O inverso x(F) pode não existir porque a função de distribuição cumulativa tem intervalos de valores constantes. No entanto, a fórmula anterior ainda pode ser aplicada generalizando a definição de x(F):

x(F1)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =inf(Sim.:F(Sim.)≥ ≥ F1?{displaystyle x(F_{1})=inf{y:F(y)geq F_{1}}}

Para obter um exemplo de curva de Lorenz, consulte a distribuição de Pareto.

Propriedades

Um exemplo prático de uma curva de Lorenz: as curvas de Lorenz da Dinamarca, Hungria e Namíbia

Uma curva de Lorenz sempre começa em (0,0) e termina em (1,1).

A curva de Lorenz não é definida se a média da distribuição de probabilidade for zero ou infinita.

A curva de Lorenz para uma distribuição de probabilidade é uma função contínua. No entanto, as curvas de Lorenz representando funções descontínuas podem ser construídas como o limite das curvas de Lorenz de distribuições de probabilidade, sendo a linha de desigualdade perfeita um exemplo.

As informações em uma curva de Lorenz podem ser resumidas pelo coeficiente de Gini e pelo coeficiente de assimetria de Lorenz.

A curva de Lorenz não pode subir acima da linha de igualdade perfeita.

Uma curva de Lorenz que nunca cai abaixo de uma segunda curva de Lorenz e pelo menos uma vez passa por cima dela, tem domínio de Lorenz sobre a segunda.

Se a variável que está sendo medida não pode assumir valores negativos, a curva de Lorenz:

• não pode afundar abaixo da linha de desigualdade perfeita,
• está aumentando.

Observe, no entanto, que uma curva de Lorenz para patrimônio líquido começaria negativa devido ao fato de que algumas pessoas têm patrimônio líquido negativo por causa de dívidas.

A curva de Lorenz é invariante sob escala positiva. Se X é uma variável aleatória, para qualquer número positivo c a variável aleatória c X tem a mesma curva de Lorenz que X.

A curva de Lorenz é invertida duas vezes, uma vez sobre F = 0,5 e uma vez sobre L = 0,5, por negação. Se X é uma variável aleatória com curva de Lorenz L_X( F), então −X tem a curva de Lorenz:

L _{- Sim. X} = 1 − L _X (1-)F)

A curva de Lorenz é alterada por translações, de modo que o intervalo de igualdade F − L(F) muda proporcionalmente à razão da meios originais e traduzidos. Se X for uma variável aleatória com uma curva de Lorenz L _X (F) e média μ _X , então para qualquer constante c ≠ − μ _X , X + c tem uma curva de Lorenz definida por:

F- Sim. - Sim. LX+c(F)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ Xμ μ X+c(F- Sim. - Sim. LX(F))Não. F-L_{X+c}(F)={frac _{X}} _{X}+c}}(F-L_{X}(F)}

Para uma função de distribuição cumulativa F(x) com média μ e inversa (generalizada) x(F), então para qualquer F com 0 < F < 1:

• Se a curva Lorenz for diferenciável:
  DL(F)DF= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x(F)μ μ {displaystyle {frac {dL(F)}{dF}}={frac {x(F)}{mu }}}

  
• Se a curva Lorenz for duas vezes diferenciável, então a função de densidade de probabilidade f(x) existe nesse ponto e:
  D2L(F)DF2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1μ μ f(x(F)){displaystyle {frac {d^{2}L(F)}{dF^{2}}}={frac {1}{mu ,f(x(F)}},}

  
• Se L(F) é continuamente diferenciável, então o tangente de L(F) é paralelo à linha de igualdade perfeita no ponto F(μ). Este é também o ponto em que a diferença de igualdade F- Sim.L(F), a distância vertical entre a curva de Lorenz e a linha de igualdade perfeita, é maior. O tamanho da lacuna é igual à metade da média relativa desvio absoluto:
  F(μ μ )- Sim. - Sim. L(F(μ μ ))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =desvio absoluto médio2μ μ {displaystyle F(mu)-L(F(mu))={frac {text{mean absoluto desvio}}{2,mu }}}