Cuboctaedro

ImprimirCitar

Poliedro com 8 faces triangulares e 6 faces quadradas

Anúncio grátis para sua empresa
(Clique aqui para girar modelo)
Tipo	Solidariedade arqueológica Poliéster uniforme
Elementos	F - 14, E - 24, V = 12 (χ = 2)
Faces por lados	8
Notação de saída	AC AA
Símbolos de Schläfli	r{4,3} ou ${begin{Bmatrix}4\3end{Bmatrix}}$ rr{3,3} ou $r{begin{Bmatrix}3\3end{Bmatrix}}$
Símbolos de Schläfli	)₁{4,3} ou t_0,2(3,3)
Símbolo de Wythoff	2 \| 3 4 3 3 \| 2
Diagrama de Coxeador	ou ou
Grupo de simetria	Oh, B₃[4,3], (432), ordem 48 Td, [3,3], (332), ordem 24
Grupo de rotação	[4,3]⁺, (432), ordem 24
Ângulo dihedral	125.26° arcsec(−√3)
Referências	U₀₇C₁₉,₁₁
Propriedades	Semiregular convexo quasiregular
Rostos coloridos	3.4.3.4 (Vertex figure)
Dodecahedron Rhombic (poliédron dual)	Rede

Modelo 3D de um cuboctahedron

Um cuboctaedro é um poliedro com 8 faces triangulares e 6 faces quadradas. Um cuboctaedro tem 12 vértices idênticos, com 2 triângulos e 2 quadrados que se encontram em cada um, e 24 arestas idênticas, cada uma separando um triângulo de um quadrado. Como tal, é um poliedro quasiregular, ou seja, um sólido arquimediano que não é apenas transitivo de vértice, mas também transitivo de aresta. É radialmente equilátero.

Seu poliedro dual é o dodecaedro rômbico.

O cuboctaedro provavelmente era conhecido de Platão: as Definitiones de Heron citam Arquimedes dizendo que Platão conhecia um sólido feito de 8 triângulos e 6 quadrados.

Sinônimos

Equilíbrio de vetores (Buckminster Fuller) porque o seu raio centro-a-vertex é igual ao seu comprimento de borda (tem simetria equilateral radial). Fuller também chamado de cuboctahedron construído de struts rígidos e vértices flexíveis um jitterbug; este objeto pode ser progressivamente transformado em um icosahedron, octahedron e tetrahedron dobrando ao longo das diagonais de seus lados quadrados.
Com O_h simetria, ordem 48, é uma cubo retificado ou retificado octahedron (Norman Johnson)
Com T_D simetria, ordem 24, é um tetraedro de cantela ou rhombitetratetrahedron.
Com D_3D simetria, ordem 12, é um gyrobicupola triangular.

Projeções ortogonais

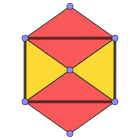
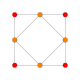
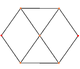
O cuboctaedro tem quatro projeções ortogonais especiais, centradas em um vértice, uma aresta e os dois tipos de faces, triangular e quadrada. Os dois últimos correspondem aos planos B₂ e A₂ de Coxeter. As projeções enviesadas mostram um quadrado e um hexágono passando pelo centro do cuboctaedro.

Cuboctahedron (projeções ortogonais)
Praça Cara	Triangular Cara	Verbos	Borda


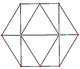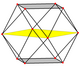[4]	[6]	[2]	[2]
Dodecahedron Rhombic (Poedro habitual)

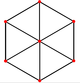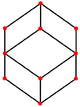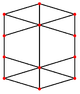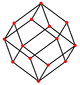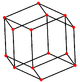Telha esférica

O cuboctaedro também pode ser representado como um ladrilho esférico e projetado no plano por meio de uma projeção estereográfica. Essa projeção é conforme, preservando ângulos, mas não áreas ou comprimentos. Linhas retas na esfera são projetadas como arcos circulares no plano.

projeção ortodoxa	quadrado-centrado	triângulo centrado	Vertex centralizado

projeção ortodoxa	Projeção estereográfica

Estrutura

Coordenadas

As coordenadas cartesianas para os vértices de um cuboctaedro (de comprimento de aresta √2 ) centrados na origem são:

(±1, ± 1,0)

(±1,0,±1)

(0,±1,±1)

Um conjunto alternativo de coordenadas pode ser feito em 4 espaços, como 12 permutações de:

(0,1,2)

Esta construção existe como uma das 16 facetas ortantes das 16 células canteladas.

Vetores raiz

Os 12 vértices do cuboctaedro podem representar os vetores raiz do grupo de Lie simples A₃. Com a adição de 6 vértices do octaedro, esses vértices representam os 18 vetores raiz do grupo de Lie simples B₃.

Propriedades da métrica

A área A e o volume V do cuboctaedro de aresta a são:

{displaystyle {begin{aligned}A&=left(6+2{sqrt {3}}right)a^{2}&&approx 9.464,1016a^{2}\V&={tfrac {5}{3}}{sqrt {2}}a^{3}&&approx 2.357,0226a^{3}.end{aligned}}}

Dissecção

Tetraedros e Octaedros

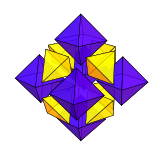
O cuboctaedro pode ser dividido em 6 pirâmides quadradas e 8 tetraedros reunidos em um ponto central. Essa dissecação é expressa no favo de mel tetraédrico-octaédrico, onde pares de pirâmides quadradas são combinados em octaedros.

Polyedros irregulares

O cuboctaedro pode ser dividido em duas cúpulas triangulares por um hexágono comum passando pelo centro do cuboctaedro. Se essas duas cúpulas triangulares forem torcidas de forma que triângulos e quadrados se alinhem, o sólido de Johnson J₂₇, a ortobicúpula triangular, é criado.

Relações geométricas

A progressão entre um tetraedro, expandido em um cuboctahedron, e reverso expandido para o tetraedro duplo

Simetria equilátera radial

Em um cuboctaedro, o raio maior (do centro ao vértice) é igual ao comprimento da aresta; assim, seu diâmetro longo (vértice a vértice oposto) é de 2 comprimentos de aresta. Seu centro é como o vértice apical de uma pirâmide: um comprimento de aresta distante de todos os outros vértices. (No caso do cuboctaedro, o centro é de fato o ápice de 6 pirâmides quadradas e 8 triangulares). Essa simetria equilátera radial é uma propriedade de apenas alguns politopos uniformes, incluindo o hexágono bidimensional, o cuboctaedro tridimensional e o quadridimensional de 24 células e 8 células (tesserato). Os politopos radialmente equiláteros são aqueles que podem ser construídos, com seus raios longos, a partir de triângulos equiláteros que se encontram no centro do politopo, cada um contribuindo com dois raios e uma aresta. Portanto, todos os elementos interiores que se encontram no centro desses politopos têm faces internas triangulares equiláteras, como na dissecação do cuboctaedro em 6 pirâmides quadradas e 8 tetraedros.

Cada um desses polítopos radialmente equiláteros também ocorre como células de uma tesselação característica de preenchimento de espaço: o ladrilho de hexágonos regulares, o favo de mel cúbico retificado (de cuboctaedros e octaedros alternados), o favo de mel de 24 células e o favo de mel tesserático, respectivamente. Cada mosaico tem um mosaico duplo; os centros das células em um mosaico são vértices de células em seu mosaico dual. O empacotamento regular de esferas mais denso conhecido em duas, três e quatro dimensões usa os centros das células de um desses mosaicos como centros de esferas.

Um cuboctaedro tem simetria octaédrica. Sua primeira estrelação é composta de um cubo e seu octaedro dual, com os vértices do cuboctaedro localizados nos pontos médios das arestas de ambos.

Construções

Um cuboctaedro pode ser obtido tomando uma seção transversal equatorial de uma célula quadridimensional de 24 ou 16 células. Um hexágono ou um quadrado pode ser obtido tomando uma seção transversal equatorial de um cuboctaedro.

O cuboctaedro é um cubo retificado e também um octaedro retificado.

É também um tetraedro cantelado. Com esta construção é dado o símbolo Wythoff: 3 3 | 2.

Uma cantelação enviesada do tetraedro produz um sólido com faces paralelas às do cuboctaedro, ou seja, oito triângulos de dois tamanhos e seis retângulos. Enquanto suas arestas são desiguais, este sólido permanece uniforme de vértice: o sólido tem o grupo de simetria tetraédrica completo e seus vértices são equivalentes sob esse grupo.

As arestas de um cuboctaedro formam quatro hexágonos regulares. Se o cuboctaedro for cortado no plano de um desses hexágonos, cada metade é uma cúpula triangular, um dos sólidos de Johnson; o próprio cuboctaedro também pode ser chamado de girobicúpula triangular, o mais simples de uma série (além do girobifastígio ou "girobicúpula digonal"). Se as metades forem unidas novamente com uma torção, de modo que triângulos encontrem triângulos e quadrados encontrem quadrados, o resultado é outro sólido de Johnson, a ortobicúpula triangular, também chamada de anticuboctaedro.

Ambas as bicúpulas triangulares são importantes no empacotamento das esferas. A distância do centro do sólido aos seus vértices é igual ao comprimento da aresta. Cada esfera central pode ter até doze vizinhos e, em uma rede cúbica centrada na face, eles assumem as posições dos vértices de um cuboctaedro. Em uma rede hexagonal compacta, eles correspondem aos cantos da ortobicúpula triangular. Em ambos os casos, a esfera central assume a posição do centro do sólido.

Cuboctaedros aparecem como células em três dos favos de mel uniformes convexos e em nove dos 4-polítopos uniformes convexos.

O volume do cuboctaedro é 5/6 do cubo envolvente e 5/8 do octaedro envolvente.

Arranjo de vértices

Por ser radialmente equilátero, o centro do cuboctaedro pode ser tratado como um 13º vértice apical canônico, um comprimento de aresta distante dos 12 vértices comuns, como o ápice de uma pirâmide canônica é um comprimento de aresta equidistante de seus outros vértices.

O cuboctaedro compartilha suas bordas e arranjo de vértices com dois poliedros uniformes não convexos: o cubohemioctaedro (tendo as faces quadradas em comum) e o octahemioctaedro (tendo as faces triangulares em comum), ambos têm quatro hexágonos. Também serve como um tetraedro cantelado, como sendo um tetraedro retificado.

Anúncio grátis para sua empresa	seu equador	Anúncio grátis para sua empresa	O que é isso?

O cuboctaedro 2-cobre o tetrahemihexaedro, que, portanto, tem a mesma figura de vértice abstrato (dois triângulos e dois quadrados: 3.4.3.4) e metade dos vértices, arestas e faces. (O valor real do vértice do tetra-hexaedro é 3,4.3/2.4, com um fator/2 devido ao cruzamento.)

Anúncio grátis para sua empresa	Produtos químicos

Cinemática

Progressões entre um octahedron, pseudoicosahedron e cuboctahedron. O cuboctahedron pode flexionar desta forma mesmo se suas bordas (mas não seus rostos) são rígidas.

Quando interpretado como uma estrutura de faces planas rígidas, conectadas ao longo das bordas por dobradiças, o cuboctaedro é uma estrutura rígida, como todos os poliedros convexos, pelo teorema de Cauchy. No entanto, quando as faces são removidas, deixando apenas arestas rígidas conectadas por juntas flexíveis nos vértices, o resultado não é um sistema rígido (ao contrário dos poliedros cujas faces são todas triângulos, aos quais o teorema de Cauchy se aplica apesar das faces ausentes).

Adicionando um vértice central, conectado por arestas rígidas a todos os outros vértices, subdivide o cuboctaedro em pirâmides quadradas e tetraedros, que se encontram no vértice central. Ao contrário do próprio cuboctaedro, o sistema resultante de arestas e juntas é rígido e faz parte da estrutura de treliça do octeto infinito.

Polítopos relacionados

Poliedros regulares

O cuboctaedro faz parte de uma família de poliedros uniformes relacionados ao cubo e ao octaedro regular.

Poliedros octahedral uniforme
Simetria: [4,3], (*432)							[4,3]⁺ (432)	[2]⁺[3,3] (*332)		[3]⁺,4] (3*2)
{4,3}	Não.	R{4,3} RECURSOS^1.1?	T3,4 )^1.1?	{3,4} (^1.1?	rr,3 S₂{3,4}	Não.	Sr.	H{4,3} (3,3)	H2{4,3} T3,3	- Sim. )^1.1?

		= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =				= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ou	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ou	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Duals para polihedra uniforme
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V3	V3.62	V35

O cuboctaedro também tem simetria tetraédrica com duas cores de triângulos.

Família de polihedra tetraedral uniforme
Simetria: [3,3], (*332)							[3,3]⁺, (332)


(3,3)	T3,3	R3,3	T3,3	(3,3)	rr{3,3]	3,3	Sr.
Duals para polihedra uniforme

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Poliedros quasiregulares e ladrilhos

O cuboctaedro existe em uma sequência de simetrias de poliedros quasiregulares e ladrilhos com configurações de vértice (3.n)², progredindo de ladrilhos da esfera ao plano euclidiano e no plano hiperbólico. Com a simetria da notação orbital de *n32, todos esses ladrilhos são construídos dentro de um domínio fundamental de simetria, com pontos geradores no canto do ângulo reto do domínio.

*n32 simetrias orbifold de camadas quasiregulares: (3.n)²
Construção	Esférica			Euclidiano	Hyperbolic
Construção	*332	*432	* 532	*632	*732	*832...	* ∞32
Quantidade números
Verbos	(3.3)2	(3.4)2	(3.5)2	(3.6)2	(3.7)2	(3.8)2	(3.∞)2

*n42 mutações de simetria de camadas quasiregulares: (4.n)² v ) e
Simetria *4n2 [n]	Esférica	Euclidiano	Hiperbólica compacta				Paracompactar	Não compacto
Simetria *4n2 [n]	*342 [3,4]	*442 [4]	* 542 [5]	* 642 [6]	*742 [7]	* 842 [8,4]...	* ∞42 [∞,4]	Não.ni,4]
Figuras
Config.	(4.3)2	(4.4)2	(4.5)2	(4,6)2	(4.7)2	(4.8)2	(4.∞)2	(4.nI)²

Este poliedro está topologicamente relacionado como parte da sequência de poliedros cantelados com figura de vértice (3.4.n.4), e continua como ladrilhos do plano hiperbólico. Essas figuras transitivas de vértice têm (*n32) simetria reflexiva.

*n32 mutação simetria de camadas expandidas: 3.4.n.4
Simetria *n32 [n,3]	Esférica				Euclid.	Hiperb compacto.		Paracomp.
Simetria *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	* 532 [5,3]	*632 [6,3]	*732 [7,3]	* 832 [8,3]...	* ∞32 [∞,3]
Figura
Config.	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.	3.4.8.4	3.4.∞.4

Politopos quadridimensionais

Projeções ortogonais de 24 células

O cuboctaedro pode ser decomposto em um octaedro regular e oito octaedros irregulares, mas iguais, na forma da casca convexa de um cubo com dois vértices opostos removidos. Essa decomposição do cuboctaedro corresponde à projeção paralela da primeira célula da célula 24 em três dimensões. Sob essa projeção, o cuboctaedro forma o envelope de projeção, que pode ser decomposto em seis faces quadradas, um octaedro regular e oito octaedros irregulares. Esses elementos correspondem às imagens de seis das células octaédricas na célula 24, as células mais próximas e mais distantes do ponto de vista 4D e os oito pares de células restantes, respectivamente.

Gráfico cuboctaédrico

No campo matemático da teoria dos grafos, um gráfico cuboctaédrico é o gráfico dos vértices e arestas do cuboctaedro, um dos sólidos arquimedianos. Também pode ser construído como o gráfico de linha do cubo. Tem 12 vértices e 24 arestas, é localmente linear e é um grafo arquimediano quártico.

projeção ortogonal
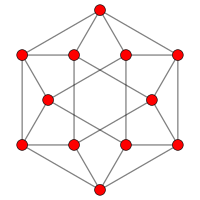Simetria de 6 vezes

Contenido relacionado

Más resultados...