Convolução

ImprimirCitar

Integral expressando a quantidade de sobreposição de uma função como é deslocada sobre outra

Comparação visual de convolução, correlação cruzada e autocorrelação. Para as operações que envolvem a função

f

, e assumindo a altura de

f

é 1.0, o valor do resultado em 5 pontos diferentes é indicado pela área sombreada abaixo de cada ponto. A simetria de

f

é a razão

fstar g

{displaystyle g*f}

são idênticos neste exemplo.

Em matemática (em particular, análise funcional), convolução é uma operação matemática em duas funções ( $f$ e $g$ ) que produz uma terceira função ( $f*g$ ) que exprime como a forma de um é modificada pelo outro. O termo convolução refere-se tanto à função de resultado e ao processo de computá-la. É definido como a integral do produto das duas funções após uma é refletida sobre o eixo y e deslocado. A escolha de qual função é refletida e deslocada antes que a integral não mude o resultado integral (veja comutatividade). A integral é avaliada para todos os valores da mudança, produzindo a função de convolução.

Algumas características da convolução são semelhantes à correlação cruzada: para funções de valor real, de uma variável contínua ou discreta, convolução ( $f*g$ ) difere da correlação cruzada ( $fstar g$ ) apenas na mesma $f (x)$ ou $g (x)$ é refletido sobre o eixo y em convolução; assim, é uma correlação cruzada de $g (x)$ e $f (x)$ ou $f (x)$ e $g (x)$ . Para funções de valor complexo, o operador de correlação cruzada é o conjunto do operador de convolução.

A convolução tem aplicações que incluem probabilidade, estatística, acústica, espectroscopia, processamento de sinal e processamento de imagem, geofísica, engenharia, física, visão computacional e equações diferenciais.

A convolução pode ser definida para funções no espaço euclidiano e outros grupos (como estruturas algébricas). Por exemplo, funções periódicas, como a transformada de Fourier de tempo discreto, podem ser definidas em um círculo e convoluídas por convolução periódica. (Consulte a linha 18 em DTFT § Propriedades.) Uma convolução discreta pode ser definida para funções no conjunto de números inteiros.

As generalizações da convolução têm aplicações no campo da análise numérica e da álgebra linear numérica, e no projeto e implementação de filtros finitos de resposta ao impulso no processamento de sinais.

O cálculo do inverso da operação de convolução é conhecido como deconvolução.

Definição

A convolução de $f$ e $g$ é escrito $f * g$ , denotando o operador com o símbolo $*$ . É definido como a integral do produto das duas funções depois que uma é refletida sobre o eixo y e deslocada. Como tal, é um tipo particular de transformação integral:

{displaystyle (f*g)(t):=int _{-infty }^{infty }f(tau)g(t-tau),dtau.}

Uma definição equivalente é (ver comutatividade):

{displaystyle (f*g)(t):=int _{-infty }^{infty }f(t-tau)g(tau),dtau.}

Enquanto o símbolo $)$ é usado acima, não precisa representar o domínio do tempo. Em cada ), a fórmula de convolução pode ser descrita como a área sob a função $f (?)$ ponderado pela função $g (?)$ deslocado pelo montante $)$ . Como $)$ alterações, a função de ponderação $g () - Sim. ?)$ enfatiza diferentes partes da função de entrada $f (?)$ Se $)$ é um valor positivo, então $g () - Sim. ?)$ é igual a $g (?)$ que desliza ou é deslocado ao longo do $tau$ - eixo para a direita (para a frente $+\infty$ ) pela quantidade de $)$ , enquanto se $)$ é um valor negativo, então $g () - Sim. ?)$ é igual a $g (?)$ que desliza ou é deslocado para a esquerda (para a frente $- \infty$ ) pela quantidade de $|t|$ .

Para funções $f$ , $g$ suportado apenas em $[0, \infty]$ (ou seja, zero para argumentos negativos), os limites de integração podem ser truncados, resultando em:

{displaystyle (f*g)(t)=int _{0}^{t}f(tau)g(t-tau),dtau quad {text{for }}f,g:[0,infty)to mathbb {R}.}

Para a formulação multidimensional de convolução, consulte domínio de definição (abaixo).

Notação

Uma convenção de notação de engenharia comum é:

{displaystyle f(t)*g(t)mathrel {:=} underbrace {int _{-infty }^{infty }f(tau)g(t-tau),dtau } _{(f*g)(t)},}

que deve ser interpretado com cuidado para evitar confusão. Por exemplo, $f (t)* g (t - t 0)$ é equivalente a $(f * g)(t - t 0)$ , mas $f (t - t 0)* g (t - t 0)$ é de fato equivalente a $(f * g)(t - 2 t 0)$ .

Relações com outras transformações

Dadas duas funções ${displaystyle f(t)}$ e $g(t)$ com transformações Laplace bilaterais (transforma Laplace de dois lados)

{displaystyle F(s)=int _{-infty }^{infty }e^{-su} f(u) {text{d}}u}

{displaystyle G(s)=int _{-infty }^{infty }e^{-sv} g(v) {text{d}}v}

respectivamente, a operação de convolução ${displaystyle (f*g)(t)}$ pode ser definido como a transformação de Laplace inversa do produto do ${displaystyle F(s)}$ e ${displaystyle G(s)}$ . Mais precisamente,

{displaystyle {begin{aligned}F(s)cdot G(s)&=int _{-infty }^{infty }e^{-su} f(u) {text{d}}ucdot int _{-infty }^{infty }e^{-sv} g(v) {text{d}}v\&=int _{-infty }^{infty }int _{-infty }^{infty }e^{-s(u+v)} f(u) g(v) {text{d}}u {text{d}}vend{aligned}}}

Vamos. ${displaystyle t=u+v}$ tal que

{displaystyle {begin{aligned}F(s)cdot G(s)&=int _{-infty }^{infty }int _{-infty }^{infty }e^{-st} f(u) g(t-u) {text{d}}u {text{d}}t\&=int _{-infty }^{infty }e^{-st}underbrace {int _{-infty }^{infty }f(u) g(t-u) {text{d}}u} _{(f*g)(t)} {text{d}}t\&=int _{-infty }^{infty }e^{-st}(f*g)(t) {text{d}}tend{aligned}}}

Note que ${displaystyle F(s)cdot G(s)}$ é a transformação bilateral de Laplace ${displaystyle (f*g)(t)}$ . Uma derivação semelhante pode ser feita usando a transformada Laplace unilateral (transforma Laplace unilateral).

A operação de convolução também descreve a saída (em termos de entrada) de uma importante classe de operações conhecida como linear invariante no tempo (LTI). Consulte a teoria do sistema LTI para obter uma derivação de convolução como resultado de restrições LTI. Em termos das transformadas de Fourier da entrada e saída de uma operação LTI, nenhum novo componente de frequência é criado. Os existentes são apenas modificados (amplitude e/ou fase). Em outras palavras, a transformada de saída é o produto pontual da transformada de entrada com uma terceira transformada (conhecida como função de transferência). Veja o teorema da convolução para obter uma derivação dessa propriedade da convolução. Por outro lado, a convolução pode ser derivada como a transformada de Fourier inversa do produto pontual de duas transformadas de Fourier.

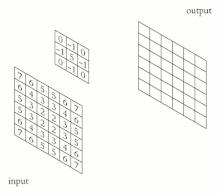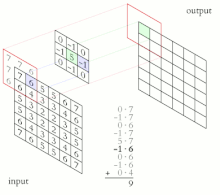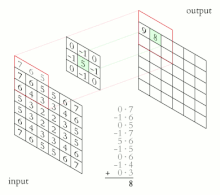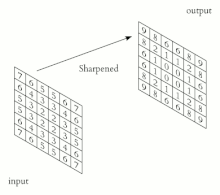
Explicação visual

Expresse cada função em termos de uma variável fictícia $tau.$ Refletir uma das funções: $g(tau)$ → $g(-tau).$ Adicionar um time-offset $)$ , que permite ${displaystyle g(-tau)}$ para deslizar ao longo do $tau$ -axis. Se $)$ é um valor positivo, então $g(t-tau)$ é igual a ${displaystyle g(-tau)}$ que desliza ou é deslocado ao longo do $tau$ - eixo para a direita (para a frente $+\infty$ ) pela quantidade de $)$ . Se $)$ é um valor negativo, então $g(t-tau)$ é igual a ${displaystyle g(-tau)}$ que desliza ou é deslocado para a esquerda (para a frente $- \infty$ ) pelo montante de \| $)$ \|. Começar $)$ em $- Não.$ e deslizar todo o caminho para $+\infty$ . Onde quer que as duas funções se cruzem, encontre a integral de seu produto. Em outras palavras, a tempo $)$ , compute a área sob a função $f(tau)$ ponderado pela função de ponderação ${displaystyle g(t-tau).}$ A forma de onda resultante (não mostrada aqui) é a convolução de funções $f$ e $g$ . Se $f ())$ é um impulso unitário, o resultado deste processo é simplesmente $g ())$ . Formalmente: ${displaystyle int _{-infty }^{infty }delta (tau)g(t-tau),dtau =g(t)}$
Neste exemplo, a cor vermelha "pulsa", ${displaystyle g(tau),}$ é uma função uniforme ${displaystyle ( g(-tau)=g(tau)),}$ assim a convolução é equivalente à correlação. Um instantâneo desta "filme" mostra funções ${displaystyle g(t-tau)}$ e $f(tau)$ (em azul) para algum valor do parâmetro $t,$ que é arbitrariamente definido como a distância ao longo da $tau$ eixo do ponto $tau = 0$ para o centro do pulso vermelho. A quantidade de amarelo é a área do produto ${displaystyle f(tau)cdot g(t-tau),}$ computado pela integral de convolução/correlação. O filme é criado mudando continuamente $t$ e recomputar a integral. O resultado (mostrado em preto) é uma função de $t,$ mas é plotado no mesmo eixo que $tau,$ para conveniência e comparação.
Nesta representação, $f(tau)$ poderia representar a resposta de um circuito de RC para um pulso estreito que ocorre em ${displaystyle tau =0.}$ Em outras palavras, se ${displaystyle g(tau)=delta (tau),}$ o resultado da convolução é apenas $f(t).$ Mas quando $g(tau)$ é o pulso mais amplo (em vermelho), a resposta é uma versão "smeared" de $f(t).$ Começa em ${displaystyle t=-0.5,}$ porque nós definimos $t$ como a distância de $tau = 0$ eixo para o centro do pulso largo (em vez da borda principal).

Desenvolvimentos históricos

Um dos primeiros usos da integral de convolução apareceu na derivação de D'Alembert do teorema de Taylor em Recherches sur différents points importants du système du monde, publicado em 1754.

Além disso, uma expressão do tipo:

{displaystyle int f(u)cdot g(x-u),du}

é usado por Sylvestre François Lacroix na página 505 de seu livro intitulado Tratado de diferenças e séries, que é o último dos 3 volumes da série enciclopédica: Traité du calcul différentiel et du calcul integral, Chez Courcier, Paris, 1797–1800. Logo depois, as operações de convolução aparecem nas obras de Pierre Simon Laplace, Jean-Baptiste Joseph Fourier, Siméon Denis Poisson e outros. O termo em si não foi amplamente utilizado até os anos 1950 ou 60. Antes disso, às vezes era conhecido como Faltung (que significa dobrar em alemão), produto de composição, integral de superposição e integral de Carson. No entanto, aparece já em 1903, embora a definição seja pouco familiar em usos mais antigos.

A operação:

<math alttext="{displaystyle int _{0}^{t}varphi (s)psi (t-s),ds,quad 0leq t∫ ∫ 0)φ φ (S)? ? ()- Sim. - Sim. S)DS,0≤ ≤ )<∞ ∞ ,{displaystyle int _{0}^{t}varphi (s)psi (t-s),ds,quad 0leq t<infty}<img alt="{displaystyle int _{0}^{t}varphi (s)psi (t-s),ds,quad 0leq t

é um caso particular de produtos de composição considerados pelo matemático italiano Vito Volterra em 1913.

Convolução circular

Quando uma função $g T$ é periódica, com período $T$ , então para funções, $f$ , tal que $f * g T$ existe, a convolução também é periódico e idêntico a:

(f*g_{T})(t)equiv int _{t_{0}}^{t_{0}+T}left[sum _{k=-infty }^{infty }f(tau +kT)right]g_{T}(t-tau),dtau

onde $t 0$ é uma escolha arbitrária. A soma é chamada de soma periódica da função $f$ .

Quando $g T$ é uma soma periódica de outra função, $g$ , então $f * g T$ é conhecido como uma convolução circular ou cíclica da classe f e $g$ .

E se a soma periódica acima for substituída por $f T$ , a operação é chamada de convolução periódica de $f T$ e $g T$ .

Convolução discreta

Animação de Convolução 2D Discreta

Para funções de valor complexo $f, g$ definidas no conjunto Z de inteiros, a convolução discreta de $f$ e $g$ é dado por:

{displaystyle (f*g)[n]=sum _{m=-infty }^{infty }f[m]g[n-m],}

ou equivalente (ver comutatividade) por:

{displaystyle (f*g)[n]=sum _{m=-infty }^{infty }f[n-m]g[m].}

A convolução de duas sequências finitas é definida pela extensão das sequências para funções finitamente suportadas no conjunto de números inteiros. Quando as sequências são os coeficientes de dois polinômios, então os coeficientes do produto ordinário dos dois polinômios são a convolução das duas sequências originais. Isso é conhecido como o produto de Cauchy dos coeficientes das sequências.

Assim quando $g$ tem suporte finito no conjunto ${-M,-M+1,dotsM-1,M}$ (representando, por exemplo, uma resposta de impulso finito), uma soma finita pode ser usada:

{displaystyle (f*g)[n]=sum _{m=-M}^{M}f[n-m]g[m].}

Convolução discreta circular

Quando uma função $g N$ é periódica, com ponto $N$ , então para funções, $f$ , tal que $f * g N$ existe, a convolução também é periódica e idêntica a:

{displaystyle (f*g_{N})[n]equiv sum _{m=0}^{N-1}left(sum _{k=-infty }^{infty }{f}[m+kN]right)g_{N}[n-m].}

A soma em $k$ é chamada de soma periódica da função $f$ .

Se $g N$ for um somatório periódico de outra função, $g$ , então $f * g N$ é conhecido como uma convolução circular de $f$ e $g$ .

Quando as durações diferentes de zero de $f$ e $g$ estão limitados ao intervalo $[0, N - 1]$ , $f * g N$ se reduz a estas formas comuns:

{displaystyle {begin{aligned}left(f*g_{N}right)[n]&=sum _{m=0}^{N-1}f[m]g_{N}[n-m]\&=sum _{m=0}^{n}f[m]g[n-m]+sum _{m=n+1}^{N-1}f[m]g[N+n-m]\[2pt]&=sum _{m=0}^{N-1}f[m]g[(n-m)_{bmod {N}}]\[2pt]&triangleq left(f*_{N}gright)[n]end{aligned}}}

(Eq.1)

A notação ( $f * N g$ ) para convolução cíclica denota a convolução sobre o grupo cíclico de inteiros módulo N.

A convolução circular surge com mais frequência no contexto da convolução rápida com um algoritmo de transformada rápida de Fourier (FFT).

Algoritmos de convolução rápida

Em muitas situações, convoluções discretas podem ser convertidas em convoluções circulares para que transformações rápidas com uma propriedade de convolução possam ser usadas para implementar a computação. Por exemplo, a convolução de sequências de dígitos é a operação central na multiplicação de números de vários dígitos, que pode, portanto, ser implementada de forma eficiente com técnicas de transformação (Knuth 1997, §4.3.3.C; von zur Gathen & Gerhard 2003, §8.2).

Eq.1 requer $N$ operações aritméticas por valor de saída e $N 2$ operações para $N$ saídas. Isso pode ser significativamente reduzido com qualquer um dos vários algoritmos rápidos. Processamento de sinal digital e outras aplicações normalmente usam algoritmos de convolução rápida para reduzir o custo da convolução para O( $N$ log $N$ ) complexidade.

Os algoritmos de convolução rápida mais comuns usam algoritmos de transformada de Fourier rápida (FFT) por meio do teorema de convolução circular. Especificamente, a convolução circular de duas sequências de comprimento finito é encontrada tomando uma FFT de cada sequência, multiplicando ponto a ponto e, em seguida, realizando uma FFT inversa. As convoluções do tipo definido acima são então implementadas eficientemente usando essa técnica em conjunto com a extensão zero e/ou descartando porções da saída. Outros algoritmos de convolução rápida, como o algoritmo de Schönhage-Strassen ou a transformada de Mersenne, usam transformadas de Fourier rápidas em outros anéis.

Se uma sequência for muito mais longa que a outra, a extensão zero da sequência mais curta e a convolução circular rápida não são os métodos computacionalmente mais eficientes disponíveis. Em vez disso, decompor a sequência mais longa em blocos e convoluir cada bloco permite algoritmos mais rápidos, como o método de sobreposição-salvar e o método de sobreposição-adicionar. Um método de convolução híbrido que combina algoritmos de bloco e FIR permite uma latência de entrada-saída zero que é útil para cálculos de convolução em tempo real.

Domínio de definição

A convolução de duas funções de valor complexo em $R d$ é em si uma função de valor complexo em $R d$ , definida por:

(f*g)(x)=int _{mathbf {R} ^{d}}f(y)g(x-y),dy=int _{mathbf {R} ^{d}}f(x-y)g(y),dy,

e está bem definido apenas se $f$ e $g$ decai suficientemente rápido no infinito para que a integral exista. As condições para a existência da convolução podem ser complicadas, uma vez que uma expansão em $g$ no infinito pode ser facilmente compensada por uma velocidade suficientemente rápida decai em $f$ . A questão da existência, portanto, pode envolver diferentes condições em $f$ e $g$ :

Funções com suporte compacto

Se $f$ e $g$ são funções contínuas compactamente suportadas, então sua convolução existe e também é compactamente suportada e contínua (Hörmander 1983, Capítulo 1). De forma mais geral, se qualquer função (digamos $f$ ) for compactamente suportada e a outra for localmente integrável, então a convolução $f * g$ é bem definido e contínuo.

Convolução de $f$ e $g$ também é bem definido quando ambas as funções são quadradas localmente integráveis em $R$ e suportadas em um intervalo da forma $[a, +\infty)$ (ou ambos suportados em $[-\infty, a]$ ).

Funções integráveis

A convolução de $f$ e $g$ existe se $f$ e $g$ são funções integráveis de Lebesgue em L1(Rd), e neste caso $f * g$ também é integrável (Stein & Weiss 1971, Teorema 1.3). Isso é uma consequência do teorema de Tonelli. Isso também é verdade para funções em $L 1$ , sob a convolução discreta, ou mais geralmente para a convolução em qualquer grupo.

Da mesma forma, se $f \in L 1$ ( $R d$ ) e $g \in L p$ ( $R d$ ) onde $1 \leq p \leq \infty$ , então $f * g \in L p$ ( $R d$ ) e

{displaystyle |{f}*g|_{p}leq |f|_{1}|g|_{p}.}

No caso particular $p = 1$ , isso mostra que $L 1$ é uma álgebra de Banach sob a convolução (e a igualdade dos dois lados vale se $f$ e $g$ são não negativos em quase todos os lugares).

Em geral, a desigualdade de Young implica que a convolução é um mapa bilinear contínuo entre $L p adequado$ espaços. Especificamente, se $1 \leq p, q, r \leq \infty$ satisfaz:

{frac {1}{p}}+{frac {1}{q}}={frac {1}{r}}+1,

então

{displaystyle leftVert f*grightVert _{r}leq leftVert frightVert _{p}leftVert grightVert _{q},quad fin {mathcal {L}}^{p}, gin {mathcal {L}}^{q},}

para que a convolução seja um mapeamento bilinear contínuo de $L p \times L q$ para $L r$ . A desigualdade de Young para convolução também é verdadeira em outros contextos (grupo de círculos, convolução em $Z$ ). A desigualdade anterior não é nítida na reta real: quando $1 < p, q, r < \infty$ , existe uma constante $B p, q < 1$ tal que:

{displaystyle leftVert f*grightVert _{r}leq B_{p,q}leftVert frightVert _{p}leftVert grightVert _{q},quad fin {mathcal {L}}^{p}, gin {mathcal {L}}^{q}.}

O valor ideal de $B p, q$ foi descoberto em 1975 e de forma independente em 1976, veja Desigualdade Brascamp-Lieb.

Uma estimativa mais forte é verdadeira, desde que $1 < p, q, r < \infty$ :

{displaystyle |f*g|_{r}leq C_{p,q}|f|_{p}|g|_{q,w}}

Onde? $|g|_{q,w}$ é a norma Lq fraca. Convolução também define um mapa contínuo bilinear ${displaystyle L^{p,w}times L^{q,w}to L^{r,w}}$ para $<math alttext="{displaystyle 1<p,q,r1<p,q,R<\infty \infty {displaystyle 1<p,q,r<infty } <img alt="1<p,q,r$ , devido à fraca desigualdade jovem:

{displaystyle |f*g|_{r,w}leq C_{p,q}|f|_{p,w}|g|_{r,w}.}

Funções de decaimento rápido

Além de funções com suporte compacto e funções integráveis, funções que têm decaimento suficientemente rápido no infinito também podem ser convoluídas. Uma característica importante da convolução é que se f e g decaem rapidamente, então f∗g também decai rapidamente. Em particular, se f e g são funções decrescentes rapidamente, então a convolução f∗g também é. Combinado com o fato de que a convolução comuta com a diferenciação (ver #Propriedades), segue-se que a classe de funções de Schwartz é fechada sob convolução (Stein & Weiss 1971, Teorema 3.3).

Distribuições

Se f é uma função suave com suporte compacto e g é uma distribuição, então f∗g é uma função suave definida por

{displaystyle int _{mathbb {R} ^{d}}{f}(y)g(x-y),dy=(f*g)(x)in C^{infty }(mathbb {R} ^{d}).}

Mais geralmente, é possível estender a definição da convolução de uma forma única com $varphi$ o mesmo f acima, de modo que a lei associativa

{displaystyle f*(g*varphi)=(f*g)*varphi }

permanece válido no caso em que f é uma distribuição e g uma distribuição compactamente suportada (Hörmander 1983, §4.2).

Medidas

A convolução de quaisquer duas medidas de Borel μ e Processo de variação limitada é a medida ${displaystyle mu *nu }$ definido por (Rudin 1962)

{displaystyle int _{mathbf {R} ^{d}}f(x),d(mu *nu)(x)=int _{mathbf {R} ^{d}}int _{mathbf {R} ^{d}}f(x+y),dmu (x),dnu (y).}

Em particular,

{displaystyle (mu *nu)(A)=int _{mathbf {R} ^{d}times mathbf {R} ^{d}}1_{A}(x+y),d(mu times nu)(x,y),}

Onde? ${displaystyle Asubset mathbf {R} ^{d}}$ é um conjunto mensurável e $1_{A}$ é a função indicadora de $A$ .

Isso concorda com a convolução definida acima quando μ e ν são considerados como distribuições, bem como a convolução das funções L¹ quando μ e ν são absolutamente contínuas em relação à medida de Lebesgue.

A convolução de medidas também satisfaz a seguinte versão da desigualdade de Young

{displaystyle |mu *nu |leq |mu ||nu |}

onde a norma é a variação total de uma medida. Como o espaço de medidas de variação limitada é um espaço de Banach, a convolução de medidas pode ser tratada com métodos padrão de análise funcional que podem não se aplicar à convolução de distribuições.

Propriedades

Propriedades algébricas

A convolução define um produto no espaço linear de funções integráveis. Este produto satisfaz as seguintes propriedades algébricas, que formalmente significam que o espaço de funções integráveis com o produto dado por convolução é uma álgebra associativa comutativa sem identidade (Strichartz 1994, §3.3). Outros espaços lineares de funções, como o espaço de funções contínuas de suporte compacto, são fechados sob a convolução e, portanto, também formam álgebras associativas comutativas.

Comutação: ${displaystyle f*g=g*f}$ Prova: Por definição: ${displaystyle (f*g)(t)=int _{-infty }^{infty }f(tau)g(t-tau),dtau }$ Alterar a variável de integração ${displaystyle u=t-tau }$ o resultado segue.

Associação: ${displaystyle f*(g*h)=(f*g)*h}$ Prova: Isso segue usando o teorema de Fubini (ou seja, integrais duplas podem ser avaliadas como integrais iteradas em qualquer ordem).

Distribuição: ${displaystyle f*(g+h)=(f*g)+(f*h)}$ Prova: Isto segue da linearidade da integralidade.

Associatividade com multiplicação escalar: ${displaystyle a(f*g)=(af)*g}$ para qualquer número real (ou complexo) $a$ .

Identidade multiplicativa: Nenhuma álgebra de funções possui uma identidade para a convolução. A falta de identidade normalmente não é uma grande inconveniência, uma vez que a maioria das coleções de funções em que a convolução é realizada pode ser convolvida com uma distribuição delta (um impulso unitário, centrado em zero) ou, pelo menos (como é o caso de L¹) admitir aproximações da identidade. O espaço linear de distribuições compactamente suportadas, no entanto, admite uma identidade sob a convolução. Especificamente, ${displaystyle f*delta =f}$ Onde? δ é a distribuição delta.

Elemento inverso: Algumas distribuições S tem um elemento inverso S^{- Sim.} para a convolução que então deve satisfazer ${displaystyle S^{-1}*S=delta }$ de que uma fórmula explícita S^{- Sim.} pode ser obtido.
O conjunto de distribuições invertíveis forma um grupo abeliano sob a convolução.

conjugação complexa: ${displaystyle {overline {f*g}}={overline {f}}*{overline {g}}}$

Relação com diferenciação: ${displaystyle (f*g)'=f'*g=f*g'}$ Prova:; ${displaystyle {begin{aligned}(f*g)'&={frac {d}{dt}}int _{-infty }^{infty }f(tau)g(t-tau),dtau \&=int _{-infty }^{infty }f(tau){frac {partial }{partial t}}g(t-tau),dtau \&=int _{-infty }^{infty }f(tau)g'(t-tau),dtau =f*g'.end{aligned}}}$

Relação com integração: Se ${textstyle F(t)=int _{-infty }^{t}f(tau)dtau}$ e ${textstyle G(t)=int _{-infty }^{t}g(tau),dtau}$ então ${displaystyle (F*g)(t)=(f*G)(t)=int _{-infty }^{t}(f*g)(tau),dtau.}$

Integração

Se f e g são funções integráveis, então a integral de sua convolução em todo o espaço é simplesmente obtida como o produto de suas integrais:

{displaystyle int _{mathbf {R} ^{d}}(f*g)(x),dx=left(int _{mathbf {R} ^{d}}f(x),dxright)left(int _{mathbf {R} ^{d}}g(x),dxright).}

Isto decorre do teorema de Fubini. O mesmo resultado vale se f e g forem considerados apenas funções mensuráveis não negativas, pelo teorema de Tonelli.

Diferenciação

No caso de uma variável,

{displaystyle {frac {d}{dx}}(f*g)={frac {df}{dx}}*g=f*{frac {dg}{dx}}}

onde d/dx é a derivada. Mais geralmente, no caso de funções de várias variáveis, uma fórmula análoga vale para a derivada parcial:

{frac {partial }{partial x_{i}}}(f*g)={frac {partial f}{partial x_{i}}}*g=f*{frac {partial g}{partial x_{i}}}.

Uma consequência particular disso é que a convolução pode ser vista como uma "suavização" operação: a convolução de f e g é diferenciável tantas vezes quanto f e g são no total.

Essas identidades são mantidas sob a condição precisa de que f e g são absolutamente integráveis e pelo menos uma delas tem um absolutamente integrável (L¹) derivada fraca, como consequência da desigualdade da convolução de Young. Por exemplo, quando f é continuamente diferenciável com suporte compacto e g é uma função localmente integrável arbitrária,

{displaystyle {frac {d}{dx}}(f*g)={frac {df}{dx}}*g.}

Essas identidades também são muito mais amplas no sentido de distribuições moderadas se um de f ou g for um distribuição temperada rapidamente decrescente, uma distribuição temperada compactamente suportada ou uma função de Schwartz e a outra é uma distribuição temperada. Por outro lado, duas funções positivas integráveis e infinitamente diferenciáveis podem ter uma convolução contínua em nenhum lugar.

No caso discreto, o operador de diferença D f(n) = f( n + 1) − f(n) satisfaz uma relação análoga:

{displaystyle D(f*g)=(Df)*g=f*(Dg).}

Teorema da convolução

O teorema da convolução afirma que

{mathcal {F}}{f*g}=kcdot {mathcal {F}}{f}cdot {mathcal {F}}{g}

Onde? ${displaystyle {mathcal {F}}{f}}$ denota a transformação de Fourier de $f$ e $k$ é uma constante que depende da normalização específica da transformação Fourier. As versões deste teorema também possuem para a transformação Laplace, a transformação Laplace de dois lados, a transformação Z-transform e a transformação de Mellin.

Por outro lado, se ${displaystyle {mathcal {W}}}$ é a matriz de transformação de Fourier, então

{displaystyle {mathcal {W}}left(C^{(1)}xast C^{(2)}yright)=left({mathcal {W}}C^{(1)}bullet {mathcal {W}}C^{(2)}right)(xotimes y)={mathcal {W}}C^{(1)}xcirc {mathcal {W}}C^{(2)}y}

Onde? ${displaystyle bullet }$ é produto de satisfação facial, $otimes$ denotes Kronecker produto, $circ$ denotes Hadamard produto (este resultado é uma evolução das propriedades do esboço da contagem).

Equivariância translacional

A convolução comuta com translações, o que significa que

{displaystyle tau _{x}(f*g)=(tau _{x}f)*g=f*(tau _{x}g)}

onde τ_xf é a tradução da função f por x definida por

{displaystyle (tau _{x}f)(y)=f(y-x).}

Se f é uma função de Schwartz, então τ_xf é a convolução com uma função delta de Dirac traduzida τ_xf = f ∗ τ_x δ. Portanto, a invariância de translação da convolução das funções de Schwartz é uma consequência da associatividade da convolução.

Além disso, sob certas condições, a convolução é a operação invariante de tradução mais geral. Informalmente falando, o seguinte vale

Suponha que S é um operador linear limitado atuando em funções que comuta com traduções: S(?_xf) = ?_x(Sf) para todos x. Então... S é dado como convolução com uma função (ou distribuição) g_S; isto é Sf = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = g_S ∗ f.

Assim, algumas operações invariantes de tradução podem ser representadas como convolução. As convoluções desempenham um papel importante no estudo de sistemas invariantes no tempo e, especialmente, na teoria de sistemas LIT. A função de representação g_S é a resposta ao impulso da transformação S.

Uma versão mais precisa do teorema citado acima requer especificar a classe de funções na qual a convolução é definida, e também requer assumir que S deve ser um operador linear contínuo em relação ao topologia apropriada. Sabe-se, por exemplo, que todo operador linear contínuo invariante de tradução contínua em L¹ é a convolução com uma medida de Borel finita. Mais geralmente, cada operador linear contínuo invariante de tradução contínua em L^p para 1 ≤ p < ∞ é a convolução com distribuição temperada cuja transformada de Fourier é limitada. Ou seja, todos eles são dados por multiplicadores de Fourier limitados.

Convoluções em grupos

Se G é um grupo adequado dotado de uma medida λ, e se f e g são funções integráveis de valor real ou complexo em G, então podemos definir sua convolução por

{displaystyle (f*g)(x)=int _{G}f(y)gleft(y^{-1}xright),dlambda (y).}

Não é comutativo em geral. Em casos típicos de interesse G é um grupo topológico Hausdorff localmente compacto e λ é uma medida (esquerda-) Haar. Nesse caso, a menos que G é unimodular, a convolução definida desta forma não é a mesma que ${textstyle int fleft(xy^{-1}right)g(y),dlambda (y)}$ . A preferência de um sobre o outro é feita de modo que a convolução com uma função fixa g comuta com tradução esquerda no grupo:

{displaystyle L_{h}(f*g)=(L_{h}f)*g.}

Além disso, a convenção também é necessária para consistência com a definição da convolução de medidas fornecida abaixo. No entanto, com uma medida de Haar à direita em vez de à esquerda, a última integral é preferida à primeira.

Em grupos abelianos localmente compactos, vale uma versão do teorema da convolução: a transformada de Fourier de uma convolução é o produto pontual das transformadas de Fourier. O grupo circular T com a medida de Lebesgue é um exemplo imediato. Para um g fixo em L¹(T), temos o seguinte operador familiar atuando no espaço de Hilbert L²(T):

{displaystyle T{f}(x)={frac {1}{2pi }}int _{mathbf {T} }{f}(y)g(x-y),dy.}

O operador T é compacto. Um cálculo direto mostra que seu adjunto T* é uma convolução com

{displaystyle {bar {g}}(-y).}

Pela propriedade de comutatividade citada acima, T é normal: T* T = TT*. Além disso, T comuta com os operadores de tradução. Considere a família S de operadores consistindo de todas essas convoluções e os operadores de tradução. Então S é uma família comutada de operadores normais. De acordo com a teoria espectral, existe uma base ortonormal {h_k} que simultaneamente diagonaliza S. Isso caracteriza convoluções no círculo. Especificamente, temos

h_{k}(x)=e^{ikx},quad kin mathbb {Z};

que são precisamente os caracteres de T. Cada convolução é um operador de multiplicação compacto nesta base. Isso pode ser visto como uma versão do teorema da convolução discutido acima.

Um exemplo discreto é um grupo cíclico finito de ordem n. Os operadores de convolução são aqui representados por matrizes circulantes e podem ser diagonalizados pela transformada discreta de Fourier.

Um resultado semelhante vale para grupos compactos (não necessariamente abelianos): os coeficientes da matriz de representações unitárias de dimensão finita formam uma base ortonormal em L² pelo Peter– Teorema de Weyl, e um análogo do teorema da convolução continua válido, junto com muitos outros aspectos da análise harmônica que dependem da transformada de Fourier.

Convolução de medidas

Seja G um grupo topológico (escrito multiplicativamente). Se μ e ν são medidas finitas de Borel em G, então sua convolução μ∗ν é definida como a medida pushforward da ação do grupo e pode ser escrito como

{displaystyle (mu *nu)(E)=iint 1_{E}(xy),dmu (x),dnu (y)}

para cada subconjunto mensurável E de G. A convolução também é uma medida finita, cuja variação total satisfaz

{displaystyle |mu *nu |leq left|mu right|left|nu right|.}

No caso em que G é localmente compacto com medida de Haar (esquerda) λ, e μ e ν são absolutamente contínuos em relação a λ, de modo que cada um tenha uma função de densidade, então o A convolução μ∗ν também é absolutamente contínua e sua função de densidade é apenas a convolução das duas funções de densidade separadas.

Se μ e ν são medidas de probabilidade no grupo topológico (R,+), então a convolução μ ∗ν é a distribuição de probabilidade da soma X + Y de duas variáveis aleatórias independentes X e Y cujas respectivas distribuições são μ e ν.

Convolução íntima

Em análise convexa, convolução infibra de apropriado (não idêntico $+infty$ ) funções convexas ${displaystyle f_{1},dotsf_{m}}$ sobre $mathbb {R} ^{n}$ é definido por:

{displaystyle (f_{1}*cdots *f_{m})(x)=inf _{x}{f_{1}(x_{1})+cdots +f_{m}(x_{m})|x_{1}+cdots +x_{m}=x}.}

{displaystyle varphi ^{*}(x)=sup _{y}(xcdot y-varphi (y)).}

{displaystyle (f_{1}*cdots *f_{m})^{*}(x)=f_{1}^{*}(x)+cdots +f_{m}^{*}(x).}

Bialgebras

Seja (X, Δ, ∇, ε, η) uma biálgebra com comultiplicação Δ, multiplicação ∇, unidade η e Conde ε. A convolução é um produto definido na álgebra de endomorfismo End(X) como segue. Seja φ, ψ ∈ End(X), ou seja, φ, ψ: X → X são funções que respeitam toda estrutura algébrica de X, então a convolução φ∗ψ é definido como a composição

{displaystyle Xmathrel {xrightarrow {Delta } } Xotimes Xmathrel {xrightarrow {phi otimes psi } } Xotimes Xmathrel {xrightarrow {nabla } } X.}

A convolução aparece notavelmente na definição das álgebras de Hopf (Kassel 1995, §III.3). Uma biálgebra é uma álgebra de Hopf se e somente se tem um antípoda: um endomorfismo S tal que

S*operatorname {id} _{X}=operatorname {id} _{X}*S=eta circ varepsilon.

Aplicativos

O blur gaussiano pode ser usado para obter uma imagem digital suave em tons de cinza de uma impressão de meio-tom.

Convolução e operações relacionadas são encontradas em muitas aplicações em ciência, engenharia e matemática.

Processamento de imagem
- Na filtragem convolucional de processamento de imagem digital desempenha um papel importante em muitos algoritmos importantes na detecção de bordas e processos relacionados (ver Kernel (processamento de imagem))
- Em óptica, uma fotografia fora de foco é uma convolução da imagem afiada com uma função de lente. O termo fotográfico para isso é bokeh.
- Em aplicações de processamento de imagem, como adicionar borragem.
No processamento digital de dados
- Em química analítica, os filtros de alisamento Savitzky-Golay são usados para a análise de dados espectroscópicos. Eles podem melhorar a relação sinal-ruído com a distorção mínima do espectro
- Em estatísticas, uma média de movimento ponderada é uma convolução.
Na acústica, a reverberação é a convolução do som original com ecos de objetos que rodeiam a fonte sonora.
- No processamento de sinal digital, a convolução é usada para mapear a resposta de impulso de uma sala real em um sinal de áudio digital.
- Em convolução de música eletrônica é a imposição de uma estrutura espectral ou rítmica em um som. Muitas vezes este envelope ou estrutura é tomado de outro som. A convolução de dois sinais é a filtragem de um através do outro.
Na engenharia elétrica, a convolução de uma função (o sinal de entrada) com uma segunda função (a resposta de impulso) dá a saída de um sistema linear de tempo-invariante (LTI). Em qualquer momento, a saída é um efeito acumulado de todos os valores anteriores da função de entrada, com os valores mais recentes tipicamente tendo a mais influência (expresso como fator multiplicativo). A função de resposta de impulso fornece esse fator como uma função do tempo decorrido desde que cada valor de entrada ocorreu.
Na física, onde quer que haja um sistema linear com um "princípio de superposição", uma operação de convolução faz uma aparição. Por exemplo, na linha de espectroscopia que se amplia devido ao efeito Doppler por conta própria dá uma forma de linha espectral Gaussiana e uma ampliação de colisão sozinha dá uma forma de linha Lorentzian. Quando ambos os efeitos estão operacionais, a forma da linha é uma convolução de Gaussian e Lorentzian, uma função Voigt.
- Na espectroscopia de fluorescência resolvida a tempo, o sinal de excitação pode ser tratado como uma cadeia de pulsos delta, e a fluorescência medida é uma soma de decaimentos exponencial de cada pulso delta.
- Em dinâmica de fluido computacional, o modelo de turbulência de grande simulação de eddy (LES) usa a operação de convolução para diminuir a escala de comprimento necessária na computação, reduzindo assim o custo computacional.
Em teoria da probabilidade, a distribuição de probabilidade da soma de duas variáveis aleatórias independentes é a convolução de suas distribuições individuais.
- Na estimativa da densidade do kernel, uma distribuição é estimada em pontos de amostra por convolução com um kernel, como um isotrópico gaussiano.
Em sistemas de planejamento de tratamento de radioterapia, a maior parte de todos os códigos modernos de cálculo aplica um algoritmo de superposição de convolução.
Na confiabilidade estrutural, o índice de confiabilidade pode ser definido com base no teorema da convolução.
- A definição de índice de confiabilidade para funções de estado limite com distribuições nãonormais pode ser estabelecida correspondente à função de distribuição conjunta. Na verdade, a função de distribuição conjunta pode ser obtida usando a teoria da convolução.
Redes neurais convolucionais aplicam múltiplas cascatas convolução kernels com aplicações em visão de máquina e inteligência artificial. Embora estes são realmente correlações cruzadas em vez de convoluções na maioria dos casos.
Na hidrodinâmica de partículas lisas, simulações de dinâmica de fluidos são calculadas usando partículas, cada uma com núcleos circundantes. Para qualquer partícula dada $i$ , alguma quantidade física $A_{i}$ é calculado como uma convolução de $A_{j}$ com uma função de ponderação, onde $j$ denota os vizinhos da partícula $i$ : aqueles que estão localizados dentro de seu kernel. A convolução é aproximada como uma soma sobre cada vizinho.
Na convolução do cálculo fracionário é fundamental em várias definições de derivado fracionário integral e fracionário.

Contenido relacionado

Más resultados...