Conjunto parcialmente ordenado
| Relações binárias transitivas | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Todas as definições requerem tacitamente a relação homogênea RNão. R. ser transitivo: para todos um,b),c,- Sim. se umRb)Não. ARB e b)Rc- Sim. então umRc.Não. |

Na matemática, especialmente na teoria da ordem, uma ordem parcial em um conjunto é um arranjo tal que, para certos pares de elementos, um precede o outro. A palavra parcial é usada para indicar que nem todo par de elementos precisa ser comparável; ou seja, pode haver pares para os quais nenhum elemento precede o outro. Ordens parciais, portanto, generalizam ordens totais, nas quais cada par é comparável.
Formalmente, uma ordem parcial é uma relação binária homogênea que é reflexiva, transitiva e antissimétrica. Um conjunto parcialmente ordenado (poset para abreviar) é um conjunto no qual uma ordem parcial é definida.
Relações de pedidos parciais
O termo ordem parcial geralmente se refere às relações reflexivas de ordem parcial, referidas neste artigo como não -strict ordens parciais. No entanto, alguns autores usam o termo para outro tipo comum de relações de ordem parcial, as relações de ordem parcial irreflexivas, também chamadas de ordens parciais estritas. Ordens parciais estritas e não estritas podem ser colocadas em uma correspondência um-para-um, portanto, para cada ordem parcial estrita, há uma ordem parcial não estrita correspondente única e vice-versa.
Pedidos parciais
A reflexivo, fracoou ordem parcial não restrita, comumente referido simplesmente como um ordem parcial, é uma relação homogênea ≤ em um conjunto PNão. P. que é reflexivo, antissimétrico, e transitivo. Isso é, para todos um,b),c∈ ∈ P,{displaystyle a,b,cin P,} deve satisfazer:
- Reflexividade: um≤ ≤ um- Sim., ou seja, cada elemento está relacionado a si mesmo.
- Antisimetria: se um≤ ≤ b)- Sim. e b)≤ ≤ umNão. então um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b)- Sim., ou seja, dois elementos distintos precedem-se.
- Transitividade: se um≤ ≤ b)- Sim. e b)≤ ≤ cNão. então um≤ ≤ c- Sim..
Uma ordem parcial não estrita também é conhecida como pré-ordem antissimétrica.
Pedidos parciais estritos
Um irreflexível, forteou ordem parcial rígida é uma relação homogênea < em conjunto PNão. P. que é irreflexível, assimétrica e transitiva; isto é, satisfaz as seguintes condições para todos um,b),c∈ ∈ P:{displaystyle a,b,cin P:}
- Irreflexividade: não <math alttext="{displaystyle aum<um- Sim.<img alt="{displaystyle a, ou seja, nenhum elemento está relacionado a si mesmo (também chamado anti-reflexivo).
- A assimetria: se <math alttext="{displaystyle aum<b)- Sim.<img alt="a então não <math alttext="{displaystyle bb)<um- Sim.<img alt="b .
- Transitividade: se <math alttext="{displaystyle aum<b)- Sim.<img alt="a e <math alttext="{displaystyle bb)<cNão. b<c)<img alt="b então <math alttext="{displaystyle aum<c- Sim.<img alt="a .
Irreflexividade e transitividade juntas implicam assimetria. Além disso, assimetria implica irreflexividade. Em outras palavras, uma relação transitiva é assimétrica se e somente se for irreflexiva. Portanto, a definição é a mesma se omitir irreflexividade ou assimetria (mas não ambas).
Uma ordem parcial estrita também é conhecida como pré-ordem estrita assimétrica.
Correspondência de relações de ordem parcial estritas e não estritas
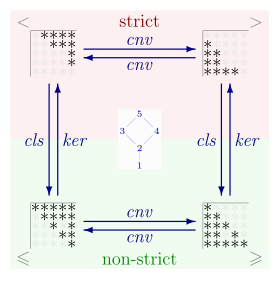
Ordens parciais rigorosas e não restritas em um conjunto PNão. P. estão intimamente relacionados. Uma ordem parcial não restrita ≤ ≤ - Sim. pode ser convertido em uma ordem parcial rigorosa, removendo todas as relações da forma um≤ ≤ um;{displaystyle aleq a;} isto é, a ordem parcial estrita é o conjunto <math alttext="{displaystyle <?≤ ≤ ∖ ∖ ? ? P{displaystyle <;:= leq \setminus Delta _{P}}<img alt="{displaystyle Onde? ? ? P?((p,p):p∈ ∈ P?{displaystyle Delta _{P}:={(p,p):pin P}} é a relação de identidade P× × PNão. Ptimes P} e ∖ ∖ {displaystyle ;setminus ;} denotes set subtraction. Por outro lado, uma estrita ordem parcial PNão. P. pode ser convertido em uma ordem parcial não restrita, unindo todas as relações dessa forma; isto é, <math alttext="{displaystyle leq ;:=;Delta _{P};cup ;≤ ≤ ?? ? PTelecomunicações Telecomunicações <{displaystyle leq ;:=;Delta _{P};cup ;<;}<img alt="{displaystyle leq ;:=;Delta _{P};cup ; é uma ordem parcial não restrita. Assim, se ≤ ≤ - Sim. é uma ordem parcial não restrita, então a ordem parcial estrita correspondente < é o kernel irreflexivo dado por
Ordens duplas
O dual (ou em frente) RONão. R^{text{op}}} de uma relação de ordem parcial RNão. R. é definido por deixar RONão. R^{text{op}}} ser a relação conversa de RNão. R., i.e. xROSim.Não. xR^{text{op}}y} se e somente se Sim.Rx- Sim.. A dupla de uma ordem parcial não restrita é uma ordem parcial não restrita, e a dupla de uma ordem parcial rigorosa é uma ordem parcial estrita. A dupla de uma dupla de uma relação é a relação original.
notação
Dado um conjunto PNão. P. e uma relação de ordem parcial, tipicamente a ordem parcial não restrita ≤ ≤ - Sim., podemos exclusivamente estender a nossa notação para definir quatro relações de ordem parcial <math alttext="{displaystyle leq}" xmlns="http://www.w3.org/1998/Math/MathML">≤ ≤ ,<,≥ ≥ ,e>{displaystyle leq}<img alt="{displaystyle leq}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/22333493c1c1bdfdd07babc8d8392833d065d5d4" style="vertical-align: -0.671ex; width:15.888ex; height:2.509ex;"/>, onde ≤ ≤ - Sim. é uma relação de ordem parcial não restrita PNão. P., <math alttext="{displaystyle <- Sim.<img alt=" é a relação de ordem parcial estrita associada PNão. P. (o núcleo irreflexivo do ≤ ≤ - Sim.), ≥ ≥ - Sim. é o dual de ≤ ≤ - Sim.e }" xmlns="http://www.w3.org/1998/Math/MathML">>Não. " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b27b77ab4e3293ea9ce65cef60fea655c398423" style="vertical-align: -0.338ex; width:1.808ex; height:1.843ex;"/> é o dual de <math alttext="{displaystyle <- Sim.<img alt=". Estritamente falando, o termo conjunto parcialmente ordenado refere-se a um conjunto com todas essas relações definidas adequadamente. Mas, praticamente, só se deve considerar uma única relação, (P,≤ ≤ )(P,leq)} ou <math alttext="{displaystyle (P,(P,<)(P,<)}<img alt="{displaystyle (P,, ou, em casos raros, as relações estritas e não restritas, <math alttext="{displaystyle (P,leq(P,≤ ≤ ,<)(P,leq<)}<img alt="{displaystyle (P,leq.
O termo conjunto ordenado é às vezes usado como um shorthand para conjunto parcialmente ordenado, desde que seja claro do contexto que nenhum outro tipo de ordem é significada. Em particular, os conjuntos totalmente ordenados também podem ser referidos como "conjuntos ordenados", especialmente em áreas onde essas estruturas são mais comuns do que posets. Alguns autores usam símbolos diferentes do que ≤ ≤ - Sim. como ⊑ ⊑ - Sim. ou ⪯ ⪯ {displaystyle preceq } para distinguir ordens parciais de ordens totais.
Ao se referir a ordens parciais, ≤ ≤ - Sim. não deve ser tomado como o complemento de }" xmlns="http://www.w3.org/1998/Math/MathML">>Não. " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b27b77ab4e3293ea9ce65cef60fea655c398423" style="vertical-align: -0.338ex; width:1.808ex; height:1.843ex;"/>. A relação }" xmlns="http://www.w3.org/1998/Math/MathML">>Não.
" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b27b77ab4e3293ea9ce65cef60fea655c398423" style="vertical-align: -0.338ex; width:1.808ex; height:1.843ex;"/> é o inverso do núcleo irreflexivo de ≤ ≤ - Sim., que é sempre um subconjunto do complemento de ≤ ≤ - Sim., mas }" xmlns="http://www.w3.org/1998/Math/MathML">>Não.
" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b27b77ab4e3293ea9ce65cef60fea655c398423" style="vertical-align: -0.338ex; width:1.808ex; height:1.843ex;"/> é igual ao complemento de ≤ ≤ - Sim. se, e somente se, ≤ ≤ - Sim. é uma ordem total.
Definições alternativas
Outra maneira de definir uma ordem parcial, encontrada na ciência da computação, é através de uma noção de comparação. Especificamente, dado <math alttext="{displaystyle leq}" xmlns="http://www.w3.org/1998/Math/MathML">≤ ≤ ,<,≥ ≥ ,e>{displaystyle leq}<img alt="{displaystyle leq}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/22333493c1c1bdfdd07babc8d8392833d065d5d4" style="vertical-align: -0.671ex; width:15.888ex; height:2.509ex;"/> como definido anteriormente, pode-se observar que dois elementos x e Sim. pode estar em qualquer um dos quatro relacionamentos mutuamente exclusivos uns com os outros: ou x<Sim.ou x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Sim.ou x>Sim.ou x e Sim. são incomparável. Isso pode ser representado por uma função <math alttext="{displaystyle {text{compare}}:Ptimes Pto {,=,vert }}" xmlns="http://www.w3.org/1998/Math/MathML">Comparar:P× × P→ → (<,>,= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =,|?{displaystyle {text{compare}}:Ptimes Pto {,=,vert }}<img alt="{displaystyle {text{compare}}:Ptimes Pto {,=,vert }}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/59682cba3ebbeca89c9a1302b978ef046ad1cf7e" style="vertical-align: -0.838ex; width:31.91ex; height:2.843ex;"/> que retorna um dos quatro códigos quando dado dois elementos. Esta definição é equivalente a uma ordem parcial em um setoid, onde a igualdade é considerada uma relação de equivalência definida em vez da noção primitiva de igualdade definida.
Wallis define uma noção mais geral de uma relação de ordem parcial como qualquer relação homogênea que é transitiva e antisimétrica. Isso inclui ordens parciais reflexivas e irreflexivas como subtipos.
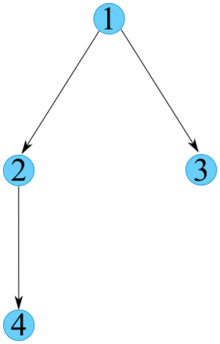
Uma poset finita pode ser visualizada através de seu diagrama de Hasse. Especificamente, tomando uma relação de ordem parcial rigorosa <math alttext="{displaystyle (P,(P,<)(P,<)}<img alt="{displaystyle (P,, um gráfico acíclico direcionado (DAG) pode ser construído tomando cada elemento de PNão. P. para ser um nó e cada elemento de <math alttext="{displaystyle <- Sim.<img alt=" para ser uma borda. A redução transitiva deste DAG é então o diagrama de Hasse. Da mesma forma, este processo pode ser reverso para construir ordens parciais rígidas de certos DAGs. Em contraste, o gráfico associado a uma ordem parcial não-strita tem auto-loops em cada nó e, portanto, não é um DAG; quando uma ordem não-strita é dito para ser representado por um diagrama de Hasse, na verdade, a ordem estrita correspondente é mostrada.
Exemplos
Exemplos padrão de poses que surgem na matemática incluem:
- Os números reais, ou em geral qualquer conjunto totalmente ordenado, ordenados pelo padrão menos do que igual relação ≤, é uma ordem parcial.
- Nos números reais R{displaystyle mathbb {R} } }, o habitual menos do que a relação R{displaystyle mathbb {R} } }.
- Por definição, cada ordem fraca estrita é uma ordem parcial rigorosa.
- O conjunto de subconjuntos de um determinado conjunto (o seu conjunto de potência) ordenados pela inclusão (ver Fig.1). Da mesma forma, o conjunto de sequências ordenadas por subsequência, e o conjunto de cadeias ordenadas por substring.
- O conjunto de números naturais equipados com a relação da divisibilidade. (ver Fig.3 e Fig.6)
- O conjunto de vértices de um grafo acíclico direcionado ordenado pela acessibilidade.
- O conjunto de subespaços de um espaço vetorial ordenado pela inclusão.
- Para um conjunto parcialmente ordenado P, o espaço de sequência contendo todas as sequências de elementos de P, onde a sequência um precede a sequência b) se cada item dentro um precede o item correspondente em b). Formalmente, (umn)n∈ ∈ N≤ ≤ (b)n)n∈ ∈ N{displaystyle left(a_{n}right)_{nin mathbb {N} }leq left(b_{n}right)_{nin mathbb Não. se e somente se umn≤ ≤ b)n{displaystyle a_{n}leq b_{n}} para todos n∈ ∈ N{displaystyle nin mathbb Não.; isto é, uma ordem de componente.
- Para um conjunto X e um conjunto parcialmente ordenado P, o espaço de função contendo todas as funções de X para P, onde f ≤ g se e somente se f(x≤ g(x) para todos x∈ ∈ X.{displaystyle xin X.}
- Uma cerca, um conjunto parcialmente ordenado definido por uma sequência alternada de relações de ordem um < b) > c < D...
- O conjunto de eventos em relatividade especial e, na maioria dos casos, relatividade geral, onde para dois eventos X e Y, X ≤ Y se e somente se Y está no futuro cone de luz de X. Um evento Y só pode ser causalmente afetado por X se X ≤ Y.
Um exemplo familiar de um conjunto parcialmente ordenado é uma coleção de pessoas ordenadas por descendência genealógica. Alguns pares de pessoas carregam a relação descendente-antepassado, mas outros pares de pessoas são incomparáveis, nenhum sendo descendente do outro.
Ordens no produto cartesiano de conjuntos parcialmente ordenados
Em ordem crescente de resistência, ou seja, conjuntos de pares decrescentes, três das possíveis ordens parciais no produto cartesiano de dois conjuntos parcialmente ordenados são (ver Fig.4):
- a ordem lexicográfica: (um, b)) ≤ (c, D) se um < c ou (um = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = c e b) ≤ D);
- a ordem do produto: (um, b)) ≤ (c, D) se um ≤ c e b) ≤ D;
- o fechamento reflexivo do produto direto das ordens estritas correspondentes: (um, b)) ≤ (c, D) se (um < c e b) < D) ou (um = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = c e b) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = D).
Todos os três podem ser definidos de forma semelhante para o produto cartesiano de mais de dois conjuntos.
Aplicado a espaços vetoriais ordenados sobre o mesmo campo, o resultado é, em cada caso, também um espaço vetorial ordenado.
Veja também ordens do produto cartesiano de conjuntos totalmente ordenados.
Somas de conjuntos parcialmente ordenados
Outra forma de combinar dois posets (disjuntos) é a soma ordinal (ou soma linear), Z = X ⊕ Y, definido na união dos conjuntos subjacentes X e Y pela ordem a ≤ Z b se e somente se:
- um, b) ∈ X com um ≤X b)ou
- um, b) ∈ Y com um ≤Y b)ou
- um ∈ X e b) ∈ Y.
Se dois posets são bem ordenados, então sua soma ordinal também é.
Ordens parciais série-paralelo são formadas a partir da operação de soma ordinal (neste contexto denominada composição série) e outra operação denominada composição paralela. A composição paralela é a união disjunta de dois conjuntos parcialmente ordenados, sem relação de ordem entre os elementos de um conjunto e os elementos do outro conjunto.
Noções derivadas
Os exemplos usam o poset (P((x,Sim.,zangão.?),⊆ ⊆ ){displaystyle ({mathcal {P}}({x,y,z}),subseteq)} consistindo do conjunto de todos os subconjuntos de um conjunto de três elementos (x,Sim.,zangão.?,{displaystyle {x,y,z},} encomendado por conjunto de inclusão (ver Fig.1).
- um o relacionados b) quando um ≤ b). Isso não implica que b) também está relacionado com um, porque a relação não precisa ser simétrica. Por exemplo, (x?{displaystyle {x}} está relacionado com (x,Sim.?,{displaystyle {x,y},} mas não o contrário.
- um e b) são comparável se um ≤ b) ou b) ≤ um. Caso contrário, incomparável. Por exemplo, (x?{displaystyle {x}} e (x,Sim.,zangão.?{displaystyle {x,y,z}} são comparáveis, enquanto (x?{displaystyle {x}} e (Sim.?{displaystyle {y}} não estão.
- A ordem total ou ordem linear é uma ordem parcial sob a qual cada par de elementos é comparável, ou seja, trichotomia detém. Por exemplo, os números naturais com sua ordem padrão.
- A cadeia é um subconjunto de um poset que é um conjunto totalmente ordenado. Por exemplo, ((?,(x?,(x,Sim.,zangão.??Não. {,},{x},{x,y,z}}} é uma corrente.
- Um Antichain é um subconjunto de uma poset em que nenhum dois elementos distintos são comparáveis. Por exemplo, o conjunto de singletons ((x?,(Sim.?,(zangão.??.Não. {{x},{y},{z}}.}
- Um elemento um é dito para ser estritamente menos do que um elemento b), se um ≤ b) e um≠ ≠ b).Não. Por exemplo, (x?{displaystyle {x}} é estritamente menos do que (x,Sim.?.{displaystyle {x,y}.}
- Um elemento um é dito para ser cobertos por outro elemento b), escrito um ⋖ b) (ou um <: b)), se um é estritamente menos do que b) e nenhum terceiro elemento c se encaixa entre eles; formalmente: se ambos um ≤ b) e um≠ ≠ b)- Sim. são verdadeiros, e um ≤ c ≤ b) é falso para cada um c com um≠ ≠ c≠ ≠ b).{displaystyle aneq cneq b.} Usando a ordem estrita <, a relação um ⋖ b) pode ser equivalentemente reformulado como "um < b) mas não um < c < b) para qualquer c". Por exemplo, (x?{displaystyle {x}} é coberto por (x,zangão.?,{displaystyle {x,z},} mas não é coberto por (x,Sim.,zangão.?.{displaystyle {x,y,z}.}
Extrema
Há várias noções de elemento "grande" e "leste" em um poset P,- Sim. nomeadamente:
- Maior elemento e menos elemento: Um elemento g∈ ∈ P{displaystyle gin P} é um maior elemento se um≤ ≤ g- Sim. para cada elemento um∈ ∈ P.{displaystyle ain P.} Um elemento m∈ ∈ P{displaystyle min P} é um menor elemento se m≤ ≤ um- Sim. para cada elemento um∈ ∈ P.{displaystyle ain P.} Uma poset só pode ter um maior ou menos elemento. Em nosso exemplo de execução, o conjunto (x,Sim.,zangão.?{displaystyle {x,y,z}} é o maior elemento, e (?{displaystyle {,}} é o mínimo.
- Elementos máximos e elementos mínimos: Um elemento g∈ ∈ P{displaystyle gin P} é um elemento máximo se não houver elemento um∈ ∈ P{displaystyle ain P} tal que g.}" xmlns="http://www.w3.org/1998/Math/MathML">um>g.- Sim.
g.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b8cc3a31a30168a980d16dd932e4c4adcdbee6db" style="vertical-align: -0.671ex; width:6.091ex; height:2.176ex;"/> Da mesma forma, um elemento m∈ ∈ P{displaystyle min P} é um elemento mínimo se não houver elemento um∈ ∈ P{displaystyle ain P} tal que <math alttext="{displaystyle aum<m.Não.<img alt="{displaystyle a Se um poset tem um elemento maior, deve ser o elemento máximo único, mas de outra forma pode haver mais de um elemento máximo, e similarmente para menos elementos e elementos mínimos. Em nosso exemplo de execução, (x,Sim.,zangão.?{displaystyle {x,y,z}} e (?{displaystyle {,}} são os elementos máximos e mínimos. Removendo estes, há 3 elementos máximos e 3 elementos mínimos (ver Fig.5).
- Limites superiores e inferiores: Para um subconjunto A de P, um elemento x em P é um limite superior de A se um≤x, para cada elemento um em A. Em particular, x não precisa estar dentro A para ser um limite superior de A. Da mesma forma, um elemento x em P é um limite inferior de A se um≥x, para cada elemento um em A. Um maior elemento de P é um limite superior de P e um elemento mínimo é um limite inferior de P. No nosso exemplo, o conjunto (x,Sim.?{displaystyle {x,y}} é um limite superior para a coleção de elementos ((x?,(Sim.??.Não. {{x},{y}}.}
Como outro exemplo, considere os inteiros positivos, ordenados pela divisibilidade: 1 é um elemento mínimo, pois divide todos os outros elementos; por outro lado este poset não tem um elemento maior. Este conjunto parcialmente ordenado nem sequer tem elementos maximais, uma vez que qualquer g divide por exemplo 2g, que é distinta dele, assim g não é maximal. Se o número 1 for excluído, mantendo a divisibilidade como ordenação sobre os elementos superiores a 1, então o poset resultante não tem um mínimo de elemento, mas qualquer número primo é um elemento mínimo para ele. Neste poset, 60 é um limite superior (embora não um limite mínimo superior) do subconjunto (2,3,5,10.?,{displaystyle {2,3,5,10},} que não tem nenhum limite inferior (desde 1 não está na poset); por outro lado 2 é um limite inferior do subconjunto de poderes de 2, que não tem nenhum limite superior. Se o número 0 for adicionado, este será o maior elemento, já que este é um múltiplo de cada inteiro (ver Fig.6).
Mapeamentos entre conjuntos parcialmente ordenados
Dado dois conjuntos parcialmente ordenados (S, ≤) e (T,)), uma função f:S→ → T{displaystyle f:Sto T} é chamado reserva de ordemou monotoniaou O que é?, se for tudo x,Sim.∈ ∈ S,{displaystyle x,yin S,} x≤ ≤ Sim.- Sim. implica f(x) f(Sim.). Se (U,)) é também um conjunto parcialmente ordenado, e ambos f:S→ → T{displaystyle f:Sto T} e g:T→ → U{displaystyle g:Tto U} são reserva de ordem, sua composição g∘ ∘ f:S→ → U{displaystyle gcirc f:Sto U} é reserva de ordem, também. Uma função f:S→ → T{displaystyle f:Sto T} é chamado Reflexão de ordem se para todos x,Sim.∈ ∈ S,{displaystyle x,yin S,} f(x) f(Sim.) implica x≤ ≤ Sim..{displaystyle xleq y.}Se f é tanto reserva de ordem e refletor de ordem, então é chamado de Incorporação de pedidos de (S, ≤) para dentro (T,)). No último caso, f é necessariamente injetável, uma vez que f(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =f(Sim.)(x)=f(y)} implica x≤ ≤ Sim.eSim.≤ ≤ x{displaystyle xleq y{text{ e }}yleq x} e por sua vez x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Sim.- Sim. de acordo com a antisimetria de ≤ ≤ .- Sim. Se uma ordem de inclusão entre dois posets S e T existe, um diz que S pode ser incorporado para dentro T. Se um pedido de entrada f:S→ → T{displaystyle f:Sto T} é bijetivo, chama-se um ordem isomorfismoe as ordens parciais (S, ≤) e (T,)) são ditos para ser isomorfo. As ordens isomórficas têm diagramas Hasse estruturalmente semelhantes (ver Fig.7a). Pode-se mostrar que se mapas de reserva de ordem f:S→ → T{displaystyle f:Sto T} e g:T→ → U{displaystyle g:Tto U} existir tal que g∘ ∘ fNão. e f∘ ∘ gNão. produz a função de identidade em S e T, respectivamente, então S e T são ordem-isomorfo.
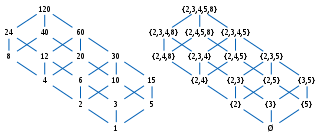
Por exemplo, um mapeamento f:N→ → P(N){displaystyle f:mathbb] {N} to mathbb {P} (mathbb {N})} do conjunto de números naturais (ordenados pela divisibilidade) para o conjunto de potência de números naturais (ordenados pela inclusão do conjunto) pode ser definido tomando cada número para o conjunto de seus principais divisores. É reserva de ordem: se x divide Sim., então cada divisor principal de x é também um grande divisor de Sim.. No entanto, não é nem injetivo (desde que mapeia tanto 12 como 6 (2,3?{displaystyle {2,3}}) nem a reflexão da ordem (desde 12 não divide 6). Tomando em vez de cada número para o conjunto de seus divisores de poder primo define um mapa g:N→ → P(N){displaystyle g:mathbb {N} to mathbb {P} (mathbb {N})} que é reserva de ordem, reflexão de ordem, e, portanto, uma entrada de ordem. Não é uma ordem-isomorfismo (já que, por exemplo, não mapeia nenhum número para o conjunto (4?Não. {4}}), mas pode ser feito um limitando o seu codomínio a g(N).{displaystyle g(mathbb {N}).} Fig.7b mostra um subconjunto de N{displaystyle mathbb {N} } } e sua imagem isomórfica sob g. A construção de tal ordem-isomorfismo em um conjunto de poder pode ser generalizada para uma ampla classe de ordens parciais, chamadas de treliças distributivas, ver "Teorema de representação de Birkhoff".
Número de pedidos parciais
A sequência A001035 no OEIS fornece o número de pedidos parciais em um conjunto de n elementos rotulados:
| Elementos | Qualquer | Transição | Reflexão | Symmetric | Pré-venda | Ordem parcial | Entidade total | Ordem total | Relação de equivalência |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 |
| 2 | 16. | 13 | 4 | 8 | 4 | 3 | 3 | 2 | 2 |
| 3 | 512 | 171 | 64 | 64 | 29 de Março | 19 | 13 | 6 | 5 |
| 4 | 65,536 | 3,994 | 4,096 | 1,024 | 355 | 219 | 75 | 24. | 15 |
| n | 2n2 | 2n2- Sim.n | 2n(n+1 / 2 | Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0nk!S(n,k)- Sim. _{k=0}^{n}k!S(n,k)} | n! | Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0nS(n,k)- Sim. S(n,k)} | |||
| OEIS | A002416 | A006905 | A053763 | A006125 | A000798 | A001035 | A000670 | A000142 | A000110 |
Observe que S(n, k) refere-se aos números de Stirling do segundo tipo.
O número de pedidos parciais estritos é igual ao de pedidos parciais.
Se a contagem for feita apenas até o isomorfismo, a sequência 1, 1, 2, 5, 16, 63, 318,... (sequência A000112 no OEIS) é obtido.
Extensão linear
Uma ordem parcial ≤ ≤ ∗ ∗ {displaystyle leq ^{*}} em um conjunto X- Sim. é um extensão de outra ordem parcial ≤ ≤ - Sim. sobre X- Sim. desde que para todos os elementos x,Sim.∈ ∈ X,{displaystyle x,yin X,} sempre x≤ ≤ Sim.,{displaystyle xleq y,} é também o caso de x≤ ≤ ∗ ∗ Sim..- Sim. Uma extensão linear é uma extensão que também é uma ordem linear (ou seja, total). Como exemplo clássico, a ordem lexicográfico de conjuntos totalmente ordenados é uma extensão linear de sua ordem de produto. Cada ordem parcial pode ser estendida a uma ordem total (princípio de ordem de extensão).
Na ciência da computação, algoritmos para encontrar extensões lineares de ordens parciais (representadas como as ordens de acessibilidade de grafos acíclicos direcionados) são chamados de classificação topológica.
Na teoria da categoria
Cada poset (e cada conjunto pré-ordenado) pode ser considerado como uma categoria onde, para objetos xNão. e Sim.,Sim. há no máximo um morfismo de xNão. para Sim..Sim. Mais explicitamente, deixe hom(x, Sim.) = (x, Sim.Se x ≤ Sim. (e de outra forma o conjunto vazio) e (Sim.,zangão.)∘ ∘ (x,Sim.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(x,zangão.).(y,z)circ (x,y)=(x,z). ? Tais categorias são por vezes chamadas posetal. Em topologia diferencial, a teoria da homologia (HT) é usada para classificar coletores lisos equivalentes M, relacionados às formas geométricas de M.
Posets são equivalentes entre si se e somente se forem isomórficos. Em um poset, o menor elemento, se existir, é um objeto inicial, e o maior elemento, se existir, é um objeto terminal. Além disso, cada conjunto pré-ordenado é equivalente a um poset. Finalmente, toda subcategoria de um poset é fechada por isomorfismo. Na topologia diferencial, a teoria da homologia (HT) é usada para classificar variedades suaves equivalentes M, relacionadas com as formas geométricas de M. Na teoria da homologia é dada uma abordagem HT axiomática, especialmente para a homologia singular. Os membros HT são invariantes algébricos sob difeomorfismos. A categoria HT axiomática é tomada em G. Kalmbach do livro Eilenberg-Steenrod (veja as referências) para mostrar que o conceito topológico teórico de conjunto para a definição de HT pode ser estendido para conjuntos ordenados parciais P. Importantes são cadeias e filtros em P (substituindo formas de M) para definir classificações HT, disponível para muitas aplicações P não relacionadas à teoria dos conjuntos.
Ordens parciais em espaços topológicos
Se PNão. P. é um conjunto parcialmente ordenado que também foi dada a estrutura de um espaço topológico, então é habitual assumir que ((um,b)):um≤ ≤ b)?{displaystyle {(a,b):aleq b\}} é um subconjunto fechado do espaço de produto topológico P× × P.Não. Ptimes P.} Sob essa suposição, as relações de ordem parcial são bem comportadas em limites no sentido de que se Limpar.Eu...→ → ∞ ∞ umEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um,{displaystyle lim _{ito infty }a_{i}=a,} e Limpar.Eu...→ → ∞ ∞ b)Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b),{displaystyle lim _{ito infty }b_{i}=b,} e para todos Eu...,- Sim. umEu...≤ ≤ b)Eu...,Não. a_{i}leq b_{i},} então um≤ ≤ b).Não.
Intervalos
Um intervalo em um poset P é um subconjunto I de P com a propriedade que, para qualquer x e y em I e qualquer z em P, se x ≤ z ≤ y, então z também está em I. (Esta definição generaliza a definição de intervalo para números reais.)
Para a ≤ b, o intervalo fechado [a, b] é o conjunto de elementos x satisfazendo a ≤ x ≤ b (ou seja, a ≤ x e x ≤ b). Ele contém pelo menos os elementos a e b.
Usando a relação estrita correspondente "<", o intervalo aberto (a, b) é o conjunto de elementos x que satisfaz a < x < b (ou seja, a < x e x < b). Um intervalo aberto pode estar vazio mesmo se a < b. Por exemplo, o intervalo aberto (0, 1) nos inteiros está vazio, pois não há inteiros Eu tal que 0 < I < 1.
Os intervalos semi-abertos [a, b) e (a, b] são definidos de forma semelhante.
Às vezes, as definições são estendidas para permitir a > b, caso em que o intervalo está vazio.
Um intervalo Eu... é limitado se houver elementos um,b)∈ ∈ P{displaystyle a,bin P} tal que Eu... ⊆ Não.um, b)]. Cada intervalo que pode ser representado em notação de intervalo é obviamente limitado, mas o converso não é verdade. Por exemplo, deixe P = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = (0,1) Telecomunicações (1, 2) Telecomunicações (2, 3) como um subposet dos números reais. O subconjunto (1, 2) é um intervalo limitado, mas não tem infim ou supremum em P, por isso não pode ser escrito em notação de intervalo usando elementos de P.
Uma poset é chamada localmente finita se cada intervalo limitado é finito. Por exemplo, os inteiros são localmente finitos sob sua ordenação natural. A ordem lexicográfica do produto cartesiano N× × N{displaystyle mathbb {N} times mathbb Não. não é localmente finito, pois (1, 2) ≤ (1, 3) ≤ (1, 4) ≤ (1, 5) ≤... ≤ (2, 1). Usando a notação de intervalo, a propriedade "um é coberto por b)" pode ser reformulado equivalentemente Não.um,b)]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(um,b)?.Não. Não.
Este conceito de um intervalo em uma ordem parcial não deve ser confundido com a classe particular de ordens parciais conhecidas como ordens de intervalo.
Contenido relacionado
Comutador
Problema da mochila
André Weil

















































































































![{displaystyle [a,b]={a,b}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c22504982538e7e532e76ad1ebfafd8abd6bb8f2)