Conjunto convexo

Ilustração de um conjunto convexo que parece um círculo deformado. O segmento de linha, ilustrado em preto acima, juntando pontos x e y, encontra-se completamente dentro do conjunto, ilustrado em verde. Uma vez que isso é verdade para qualquer local potencial de dois pontos dentro do conjunto acima, o conjunto é convexo.

Ilustração de um conjunto não-convexo. Ilustrado pelo segmento de linha acima pelo qual muda da cor preta para a cor vermelha. Exemplificando por que este conjunto acima, ilustrado em verde, é não-convexo.

Em geometria, um subconjunto de um espaço euclidiano, ou mais geralmente um espaço afim sobre os reais, é convexo se, dados quaisquer dois pontos no subconjunto, o subconjunto contém todo o segmento de linha que se junta a eles. De forma equivalente, um conjunto convexo ou uma região convexa é um subconjunto que intercepta cada linha em um único segmento de linha (possivelmente vazio). Por exemplo, um cubo sólido é um conjunto convexo, mas qualquer coisa que seja oca ou tenha um recuo, por exemplo, uma forma crescente, não é convexa.

O limite de um conjunto convexo é sempre uma curva convexa. A interseção de todos os conjuntos convexos que contêm um determinado subconjunto A do espaço euclidiano é chamada de casco convexo de A. É o menor conjunto convexo contendo A.

Uma função convexa é uma função de valor real definida em um intervalo com a propriedade de que sua epígrafe (o conjunto de pontos sobre ou acima do gráfico da função) é um conjunto convexo. A minimização convexa é um subcampo da otimização que estuda o problema de minimizar funções convexas sobre conjuntos convexos. O ramo da matemática dedicado ao estudo das propriedades de conjuntos convexos e funções convexas é chamado de análise convexa.

A noção de um conjunto convexo pode ser generalizada como descrito abaixo.

Definições

Uma função é convexa se e somente se seu epígrafo, a região (em verde) acima de seu grafo (em azul), é um conjunto convexo.

Seja S um espaço vetorial ou um espaço afim sobre os números reais ou, mais geralmente, sobre algum campo ordenado. Isso inclui espaços euclidianos, que são espaços afins. Um subconjunto C de S é convexo se, para todo x e y em C, o segmento de linha que conecta x e y está incluído em C. Isso significa que a combinação afim (1 − t)x + ty pertence a C, para todos os x e y em C, e t no intervalo [0, 1]. Isso implica que a convexidade (a propriedade de ser convexo) é invariante sob transformações afins. Isso implica também que um conjunto convexo em um espaço vetorial topológico real ou complexo é conectado por caminhos, portanto conectado.

Um conjunto C é estritamente convexo se cada ponto no segmento de linha que conecta x e y, exceto os pontos finais, está dentro do interior topológico de C. Um subconjunto convexo fechado é estritamente convexo se e somente se cada um de seus pontos de fronteira é um ponto extremo.

Um conjunto C é absolutamente convexo se for convexo e balanceado.

Os subconjuntos convexos de R (o conjunto dos números reais) são os intervalos e os pontos de R. Alguns exemplos de subconjuntos convexos do plano euclidiano são polígonos regulares sólidos, triângulos sólidos e interseções de triângulos sólidos. Alguns exemplos de subconjuntos convexos de um espaço tridimensional euclidiano são os sólidos arquimedianos e os sólidos platônicos. Os poliedros de Kepler-Poinsot são exemplos de conjuntos não convexos.

Conjunto não convexo

Um conjunto que não é convexo é chamado de conjunto não convexo. Um polígono que não é um polígono convexo às vezes é chamado de polígono côncavo, e algumas fontes geralmente usam o termo conjunto côncavo para significar um conjunto não convexo, mas a maioria das autoridades proíbe esse uso.

O complemento de um conjunto convexo, como a epígrafe de uma função côncava, às vezes é chamado de conjunto convexo reverso, especialmente no contexto de otimização matemática.

Propriedades

Dados r pontos u₁,..., u_r em um conjunto convexo S e r números não negativos λ₁,..., λ_r tal que λ₁ +... + λ_r = 1 , a combinação afim

Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Rλ λ kuk{displaystyle sum _{k=1}^{r}lambda _{k}u_{k}}

Essa combinação afim é chamada de combinação convexa de u₁,..., u_r .

Interseções e uniões

A coleção de subconjuntos convexos de um espaço vetorial, um espaço afim ou um espaço euclidiano tem as seguintes propriedades:

1. O conjunto vazio e todo o espaço são convexos.
2. A interseção de qualquer coleção de conjuntos de convexos é convexo.
3. O União de uma sequência de conjuntos convexos é convexo, se eles formam uma cadeia não crescente para inclusão. Para esta propriedade, a restrição a cadeias é importante, como a união de dois conjuntos convexos não precisa ser convexo.

Conjuntos convexos fechados

Conjuntos convexos fechados são conjuntos convexos que contêm todos os seus pontos limites. Eles podem ser caracterizados como as interseções de semi-espaços fechados (conjuntos de pontos no espaço que se situam em um dos lados de um hiperplano).

Pelo que acabou de ser dito, fica claro que tais interseções são convexas, e também serão conjuntos fechados. Para provar a recíproca, ou seja, todo conjunto convexo fechado pode ser representado como tal interseção, é necessário o teorema do hiperplano de suporte na forma que para um dado conjunto convexo fechado C e ponto P fora dele, há um semi-espaço fechado H que contém C e não P. O teorema do hiperplano de suporte é um caso especial do teorema de análise funcional de Hahn-Banach.

Conjuntos convexos e retângulos

Seja C um corpo convexo no plano (um conjunto convexo cujo interior não é vazio). Podemos inscrever um retângulo r em C tal que uma cópia homotética R de r está circunscrito em C. A razão de homotetia positiva é no máximo 2 e:

12)) Área⁡ ⁡ (R)≤ ≤ Área⁡ ⁡ (C)≤ ≤ 2)) Área⁡ ⁡ (R){displaystyle {tfrac {1}{2}}cdot operatorname {Area} (R)leq operatorname {Area} (C)leq 2cdot operatorname {Area} (r)}

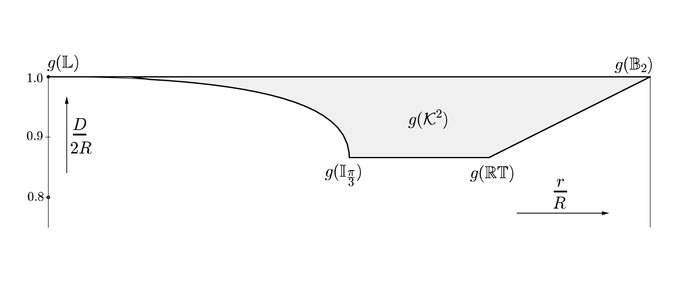
Diagramas de Blaschke-Santaló

O conjunto KK2{displaystyle {mathcal {K}}^{2}} de todos os corpos convexos planares podem ser parametrizados em termos do diâmetro do corpo convexo D, seu inradius R (o maior círculo contido no corpo convexo) e seu circunradius R (o menor círculo contendo o corpo convexo). Na verdade, este conjunto pode ser descrito pelo conjunto de desigualdades dadas por

2R≤ ≤ D≤ ≤ 2R{displaystyle 2rleq Dleq 2R}}

R≤ ≤ 33DNão. Rleq. {3}}{3}}D}

R+R≤ ≤ D{displaystyle r+Rleq D}

D24R2- Sim. - Sim. D2≤ ≤ 2R(2R+4R2- Sim. - Sim. D2)Não. D^{2} {4R^{2}-D^{2}}}leq 2R(2R+{sqrt {4R^{2}-D^{2}}})}

Blaschke-SantalóR, D, R) diagrama para corpos convexos planares. L{displaystyle mathbb {L} } } denota o segmento de linha, Eu...D D 3{displaystyle mathbb Não, não. ? o triângulo equilátero, RT- Sim. o triângulo Reuleaux e B2{displaystyle mathbb {B} _{2}} o círculo da unidade.

Alternativamente, o conjunto KK2{displaystyle {mathcal {K}}^{2}} também pode ser parametrizado pela sua largura (a menor distância entre quaisquer dois diferentes hiperplanos de suporte paralelo), perímetro e área.

Outras propriedades

Vamos. X ser um espaço vetorial topológico e C⊆ ⊆ XNão. Csubseteq X} ser convexo.

• Cl⁡ ⁡ C{displaystyle operatorname} Cl. e Int⁡ ⁡ C{displaystyle operatorname} C. são ambos convexos (ou seja, o fechamento e interior de conjuntos convexos são convexos).
• Se um∈ ∈ Int⁡ ⁡ C{displaystyle ain operatorname C. e b)∈ ∈ Cl⁡ ⁡ C{displaystyle bin operatorname} C. então Não.um,b)Não.⊆ ⊆ Int⁡ ⁡ C{displaystyle [a,b[,subseteq operatorname {Int} C}] (onde) <math alttext="{displaystyle [a,b[,:=left{(1-r)a+rb:0leq rNão.um,b)Não.?((1- Sim. - Sim. R)um+Rb):0≤ ≤ R<1?Não. [a,b[,:=left{(1-r)a+rb:0leq r<1right}}<img alt="{displaystyle [a,b[,:=left{(1-r)a+rb:0leq r).
• Se Int⁡ ⁡ C≠ ≠ ∅ ∅ {displaystyle operatorname} Cneq emptyset então:
  • cl⁡ ⁡ (Int⁡ ⁡ C)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Cl⁡ ⁡ C{displaystyle operatorname {cl} left(operatorname) (Int} Cright)=operatorname C.e
  • Int⁡ ⁡ C= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Int⁡ ⁡ (Cl⁡ ⁡ C)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =CEu...{displaystyle operatorname} C=nome do operador {Int} left(operatorname) {Cl} Cright)=C^{i}}, onde CEu...Não. C^{i}} é o interior algébrica de C.

Cascos convexos e somas de Minkowski

Cascos convexos

Cada subconjunto A do espaço vetorial está contido em um menor conjunto convexo (chamado de casco convexo de A), ou seja, a interseção de todos os conjuntos convexos contendo A . O operador de casca convexa Conv() tem as propriedades características de um operador de casca:

• extensa: S⊆ Conv(S),
• não crescente: S⊆T implica que Conv(S) ⊆ Conv(T)e
• Idempotência: Conv(Conv)S) = Conv(S).

A operação convex-hull é necessária para que o conjunto de conjuntos convexos forme uma rede, na qual a "junção" operação é o casco convexo da união de dois conjuntos convexos

Convénio⁡ ⁡ (S)∨ ∨ Convénio⁡ ⁡ (T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Convénio⁡ ⁡ (STelecomunicações Telecomunicações T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Convénio⁡ ⁡ (Convénio⁡ ⁡ (S)Telecomunicações Telecomunicações Convénio⁡ ⁡ (T)).{displaystyle operatorname {Conv} (S)vee operatorname {Conv} (T)=operatorname {Conv} (Scup T)=operatorname {Conv} {bigl (}operatorname {Conv} (S)cup operatorname {Conv} (T){bigr)}.}

Adição de Minkowski

Minkowski adição de conjuntos. A soma dos quadrados Q₁[0,1]² e Q₂Não.² é o quadrado Q₁+ Q₂Não.².

Em um espaço vetorial real, a soma de Minkowski de dois conjuntos (não vazios), S₁ e S₂, é definido como o conjunto S₁ + S₂ formado pela adição de vetores elemento a elemento da soma -conjuntos

S1+S2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(x1+x2:x1∈ ∈ S1,x2∈ ∈ S2?.Não. S_{1}+S_{2}={x_{1}+x_{2}:x_{1}in S_{1},x_{2}in S_{2}}.}

Gerenciamento Gerenciamento nSn= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(Gerenciamento Gerenciamento nxn:xn∈ ∈ Sn?.{displaystyle sum _{n}S_{n}=left{sum _{n}x_{n}:x_{n}in S_{n}right}.}

Para a adição de Minkowski, o conjunto zero {0} contendo apenas o vetor zero 0 tem importância especial: para todo subconjunto S não vazio de um espaço vetorial

S+(0?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =S;Não. S+{0}=S;}

Cascos convexos de somas de Minkowski

A adição de Minkowski se comporta bem com relação à operação de obtenção de cascas convexas, como mostra a seguinte proposição:

Seja S₁, S₂ subconjuntos de um espaço vetorial real, a cobertura convexa de sua soma de Minkowski é a soma de Minkowski de suas coberturas convexas

Convénio⁡ ⁡ (S1+S2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Convénio⁡ ⁡ (S1)+Convénio⁡ ⁡ (S2).{displaystyle operatorname} {Conv} (S_{1}+S_{2})=operatorname {Conv} (S_{1})+operatorname {Conv} (S_{2}). ?

Esse resultado é mais geral para cada coleção finita de conjuntos não vazios:

Convénio(Gerenciamento Gerenciamento nSn)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento nConvénio(Sn).{displaystyle {text{Conv}}left(sum _{n}S_{n}right)=sum _{n}{text{Conv}}left(S_{n}right).}

Na terminologia matemática, as operações de soma de Minkowski e de formação de cascas convexas são operações de comutação.

Somas de Minkowski de conjuntos convexos

A soma de Minkowski de dois conjuntos convexos compactos é compacta. A soma de um conjunto convexo compacto e um conjunto convexo fechado é fechada.

O seguinte teorema famoso, provado por Dieudonné em 1966, fornece uma condição suficiente para que a diferença de dois subconjuntos convexos fechados seja fechada. Ele usa o conceito de um cone de recessão de um subconjunto convexo não vazio S, definido como:

recreação⁡ ⁡ S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(x∈ ∈ X:x+S⊆ ⊆ S?,{displaystyle operatorname {rec} S=left{xin X,:,x+Ssubseteq Sright},}

0∈ ∈ X- Sim.

S+recreação⁡ ⁡ S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =SNão. S+operatorname {rec} S=S}

recreação⁡ ⁡ S{displaystyle operatorname {rec} S}

S0∈ ∈ S{displaystyle s_{0}in S.

0}t(S-s_{0}).}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">recreação⁡ ⁡ S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⋂ ⋂ )>0)(S- Sim. - Sim. S0).{displaystyle operatorname {rec} S=bigcap _{t>0}t(S-s_{0}). ?

0}t(S-s_{0}).}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d4d444c57a3953929f3d56e6fb432880f2853503" style="vertical-align: -3.005ex; width:20.823ex; height:5.509ex;"/>

Teorem (Dieudonné). Vamos. A e B ser subconjuntos não vazios, fechados e convexos de um espaço vetorial topológico localmente convexo tal que recreação⁡ ⁡ A─ ─ recreação⁡ ⁡ B{displaystyle operatorname {rec} Acap operatorname {rec} B} é um subespaço linear. Se A ou B é localmente compacto, então A- Sim.B está fechado.

Generalizações e extensões para convexidade

A noção de convexidade no espaço euclidiano pode ser generalizada modificando a definição em alguns ou outros aspectos. O nome comum "convexidade generalizada" é usado porque os objetos resultantes retêm certas propriedades de conjuntos convexos.

Conjuntos estrela-convexos (em forma de estrela)

Seja C um conjunto em um espaço vetorial real ou complexo. C é estrela convexa (em forma de estrela) se existir um x₀ em C de forma que a linha segmento de x₀ para qualquer ponto y em C está contido em C. Portanto, um conjunto convexo não vazio é sempre convexo em estrela, mas um conjunto convexo em estrela nem sempre é convexo.

Convexidade ortogonal

Um exemplo de convexidade generalizada é a convexidade ortogonal.

Um conjunto S no espaço euclidiano é chamado ortogonalmente convexo ou orto- convexo, se qualquer segmento paralelo a qualquer um dos eixos coordenados conectando dois pontos de S estiver totalmente dentro de S. É fácil provar que uma interseção de qualquer coleção de conjuntos ortoconvexos é ortoconvexa. Algumas outras propriedades de conjuntos convexos também são válidas.

Geometria não euclidiana

A definição de um conjunto convexo e um casco convexo se estende naturalmente a geometrias que não são euclidianas, definindo um conjunto geodesicamente convexo como aquele que contém a geodésica unindo quaisquer dois pontos no conjunto.

Topologia de ordem

A convexidade pode ser estendida para um conjunto totalmente ordenado X dotado da topologia de ordem.

Seja Y ⊆ X. O subespaço Y é um conjunto convexo se para cada par de pontos a, b em Y tal que a ≤ b, o intervalo [a, b ] = {x ∈ X | a ≤ x ≤ b} está contido em S. Ou seja, Y é convexo se e somente se para todo a, b em S, a ≤ b implica [a, b] ⊆ Y.

Um conjunto convexo não é conexo em geral: um contra-exemplo é dado pelo subespaço {1,2,3} em Z, que é convexo e não conectado.

Espaços de convexidade

A noção de convexidade pode ser generalizada para outros objetos, se certas propriedades de convexidade forem selecionadas como axiomas.

Dado um conjunto X, uma convexidade sobre o estilo X é uma coleção 𝒞 de subconjuntos do estilo X satisfazendo os seguintes axiomas:

1. O conjunto vazio e X em C
2. A interseção de qualquer coleção C em C.
3. A união de uma cadeia (com relação à relação de inclusão) de elementos de C em C.

Os elementos de 𝒞 são chamados de conjuntos convexos e o par (X, 𝒞) é chamado de espaço de convexidade. Para a convexidade ordinária, os dois primeiros axiomas são válidos e o terceiro é trivial.

Para uma definição alternativa de convexidade abstrata, mais adequada à geometria discreta, consulte as geometrias convexas associadas aos antimatróides.

Espaços convexos

A convexidade pode ser generalizada como uma estrutura algébrica abstrata: um espaço é convexo se for possível obter combinações convexas de pontos.