Conjunção lógica

Diagrama de folheado $Não. Aland Bland C}$

Na lógica, matemática e linguística, E ($- Sim.$) é o operador funcional da verdade conjunção lógica; e de um conjunto de operandos é verdadeiro se e somente se Todos de seus operandos são verdadeiros. O conjuntivo lógico que representa este operador é tipicamente escrito como $- Sim.$ ou ) .

$Não. A terra B$ é verdade se e somente se $Não. A.$ é verdade e $Não.$ é verdade, caso contrário é falso.

Um operando de uma conjunção é um conjunto.

Além da lógica, o termo "conjunção" também se refere a conceitos semelhantes em outros campos:

• Em linguagem natural, a denotação de expressões como inglês "e".
• Em linguagens de programação, a estrutura de curto-circuito e controle.
• Na teoria dos conjuntos, intersecção.
• Na teoria do retículo, conjunção lógica (grande limite inferior).
• Na lógica predicada, quantificação universal.

Notação

E é geralmente denotado por um operador infixo: em matemática e lógica, é denotado por $- Sim.$, > ou × ; em eletrônica, ) ; e em linguagens de programação, &, &&ou and. Na notação do prefixo de Jan Łukasiewicz para a lógica, o operador é KK, para polonês O que é isso?. Notavelmente, no Microsoft Excel, a função E é um operador de postfix.

Definição

Conjunção lógica é uma operação em dois valores lógicos, normalmente os valores de duas proposições, que produz um valor de true se e somente se (também conhecido como iff) ambos os seus operandos são verdadeiros.

A identidade conjuntiva é true, o que significa que adicionar AND a uma expressão com true nunca mudará o valor da expressão. De acordo com o conceito de verdade vazia, quando a conjunção é definida como um operador ou função de aridade arbitrária, a conjunção vazia (AND-ing sobre um conjunto vazio de operandos) geralmente é definida como tendo o resultado verdadeiro.

Tabela verdade

Conjunções dos argumentos à esquerda — Os bits verdadeiros formam um triângulo Sierpinski.

A tabela da verdade $Não. A terra B$:

$Não. A.$	$Não.$	$Não. Awedge B}$
É verdade.	É verdade.	É verdade.
É verdade.	Falso	Falso
Falso	É verdade.	Falso
Falso	Falso	Falso

Definido por outros operadores

Em sistemas onde a conjunção lógica não é primitiva, ela pode ser definida como

$Não. Aland B=neg (Ato neg B)}$

ou

$Não. Aland B=neg (neg Alor neg B).}$

Regras de introdução e eliminação

Como regra de inferência, a introdução de conjunção é uma forma de argumento simples e classicamente válida. A forma do argumento tem duas premissas, A e B. Intuitivamente, permite a inferência de sua conjunção.

A,

B.

Portanto, A e B.

ou em notação de operador lógico:

$Não. A,$

$Não.$

${displaystyle vdash Aland B}$

Aqui está um exemplo de um argumento que se encaixa na forma introdução à conjunção:

O Bob gosta de maçãs.

O Bob gosta de laranjas.

Portanto, Bob gosta de maçãs e Bob gosta de laranjas.

A eliminação da conjunção é outra forma de argumento simples e classicamente válida. Intuitivamente, permite a inferência de qualquer conjunção de qualquer elemento dessa conjunção.

A e B.

Portanto, A.

...ou alternativamente,

A e B.

Portanto, B.

Na notação do operador lógico:

$Não. A terra B$

$- Sim.$

...ou alternativamente,

$Não. A terra B$

$- Sim.$

Negação

Definição

Uma conjunção $Não. A terra B$ é provado falso por estabelecer ou ${displaystyle neg A}$ ou ${displaystyle neg B}$. Em termos da linguagem do objeto, isso lê

${displaystyle neg Ato neg (Aland B)}$

Esta fórmula pode ser vista como um caso especial de

$(Ato C)to (Aland B)to C)}$

quando $Não. C.$ é uma falsa proposição.

Outras estratégias de prova

Se $Não. A.$ implica ${displaystyle neg B}$, então ambos ${displaystyle neg A}$ bem como $Não. A.$ provar a conjunção falsa:

$Não. (Ato neg {}B)to neg (Aland B)}$

Em outras palavras, uma conjunção pode realmente ser provada como falsa apenas sabendo sobre a relação de seus conjuntos, e não necessariamente sobre seus valores de verdade.

Esta fórmula pode ser vista como um caso especial de

$(Ato (Bto C))to ((Aland B)to C)}$

quando $Não. C.$ é uma falsa proposição.

Qualquer um dos itens acima são provas construtivamente válidas por contradição.

Propriedades

comutatividade: sim

$Não. A terra B$	$Não. "Leftrightarrow"$	$Não. Bland A.$
	$Não. "Leftrightarrow"$

associatividade: sim

$Não.$	$- Sim.$	$(Bland C)}$	$Não. "Leftrightarrow"$			$(Aland B)}$	$- Sim.$	$Não. ~C$
	$- Sim.$		$Não. "Leftrightarrow"$		$Não. "Leftrightarrow"$		$- Sim.$

distributividade: com várias operações, especialmente com ou

$Não.$	$Não.$	$(Blor C)}$	$Não. "Leftrightarrow"$			$(Aland B)}$	$- Sim.$	$(Aland C)}$
	$Não.$		$Não. "Leftrightarrow"$		$Não. "Leftrightarrow"$		$- Sim.$

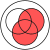outros

com exclusivo ou: $Não.$ $Não.$ $(Boplus C)}$ $Não. "Leftrightarrow"$ $(Aland B)}$ $- Sim.$ $(Aland C)}$ $Não.$ $Não. "Leftrightarrow"$ $Não. "Leftrightarrow"$ $- Sim.$ com nonimplicação material: $Não.$ $Não.$ $(Bnrightarrow C)}$ $Não. "Leftrightarrow"$ $(Aland B)}$ $- Sim.$ $(Aland C)}$ $Não.$ $Não. "Leftrightarrow"$ $Não. "Leftrightarrow"$ $- Sim.$ com si mesmo: $Não.$ $Não.$ $(Bland C)}$ $Não. "Leftrightarrow"$ $(Aland B)}$ $Não.$ $(Aland C)}$ $Não.$ $Não. "Leftrightarrow"$ $Não. "Leftrightarrow"$ $Não.$

idempotência: sim

$Não.$	$- Sim.$	$Não.$	$Não. "Leftrightarrow"$	$Não. A~$
	$- Sim.$		$Não. "Leftrightarrow"$

monotonicidade: sim

$Não. A 'direita B'$	$Não. #Rightarrow }$			$(Aland C)}$	$Não.$	$(Bland C)}$
	$Não. #Rightarrow }$		$Não. "Leftrightarrow"$		$Não.$

preservação da verdade: sim
Quando todas as entradas são verdadeiras, a saída é verdadeira.

$Não. A terra B$	$Não. #Rightarrow }$	$Não. A terra B$
	$Não. #Rightarrow }$
		(para ser testado)

preservação de falsidade: sim
Quando todas as entradas são falsas, a saída é falsa.

$Não. A terra B$	$Não. #Rightarrow }$	$Não. Alor B}$
	$Não. #Rightarrow }$
(para ser testado)

Espectro de Walsh: (1,-1,-1,1)

Não linearidade: 1 (a função é dobrada)

Se estiver usando valores binários para verdadeiro (1) e falso (0), então a conjunção lógica funciona exatamente como a multiplicação aritmética normal.

Aplicações em engenharia da computação

E portão de lógica

Na programação de computadores de alto nível e na eletrônica digital, a conjunção lógica é comumente representada por um operador infixo, geralmente como uma palavra-chave como "AND", uma multiplicação algébrica, ou o símbolo de e comercial & (às vezes dobrado como em &&). Muitas linguagens também fornecem estruturas de controle de curto-circuito correspondentes à conjunção lógica.

A conjunção lógica é freqüentemente usada para operações bit a bit, onde 0 corresponde a falso e 1 a verdadeiro:

• 0 AND 0 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0,
• 0 AND 1 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0,
• 1 AND 0 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0,
• 1 AND 1 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 1.

A operação também pode ser aplicada a duas palavras binárias vistas como cadeias de bits de igual comprimento, tomando o AND bit a bit de cada par de bits nas posições correspondentes. Por exemplo:

• 11000110 AND 10100011 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 10000010.

Isso pode ser usado para selecionar parte de uma cadeia de bits usando uma máscara de bits. Por exemplo, 10011101 AND 00001000 = 00001000 extrai o quinto bit de uma cadeia de bits de 8 bits.

Na rede de computadores, as máscaras de bits são usadas para derivar o endereço de rede de uma sub-rede dentro de uma rede existente a partir de um determinado endereço IP, por meio de AND no endereço IP e na máscara de sub-rede.

Conjunção lógica "E" também é usado em operações SQL para formar consultas de banco de dados.

A correspondência Curry-Howard relaciona a conjunção lógica aos tipos de produtos.

Correspondência teórica de conjuntos

A pertinência de um elemento de um conjunto de interseção na teoria dos conjuntos é definida em termos de uma conjunção lógica: x ∈ A ∩ B se e somente se (x ∈ A) ∧ (x ∈ B). Por meio dessa correspondência, a interseção teórica dos conjuntos compartilha várias propriedades com a conjunção lógica, como associatividade, comutatividade e idempotência.

Linguagem natural

Assim como outras noções formalizadas na lógica matemática, a conjunção lógica e está relacionada, mas não é a mesma, à conjunção gramatical e nas línguas naturais.

Inglês "e" tem propriedades não capturadas pela conjunção lógica. Por exemplo, "e" às vezes implica ordem tendo o sentido de "então". Por exemplo, "Eles se casaram e tiveram um filho" no discurso comum significa que o casamento veio antes da criança.

A palavra "e" também pode implicar uma divisão de uma coisa em partes, como "A bandeira americana é vermelha, branca e azul." Aqui, não significa que a bandeira é ao mesmo tempo vermelha, branca e azul, mas sim que tem uma parte de cada cor.