Classe de equivalência

Em matemática, quando os elementos de algum conjunto SNão. S. ter uma noção de equivalência (formalizada como uma relação de equivalência), então pode-se naturalmente dividir o conjunto SNão. S. para dentro classes de equivalência. Essas classes de equivalência são construídas para que elementos umNão. e b)Não. pertencem ao mesmo classe de equivalência se, e somente se, eles são equivalentes.
Formalmente, dado um conjunto SNão. S. e uma relação de equivalência ∼ ∼ {displaystyle ,sim ,} sobre S,Não. S, o classe de equivalência de um elemento umNão. em S,Não. S, denotado por Não.um],- Sim. é o conjunto
Quando o conjunto SNão. S. tem alguma estrutura (como uma operação em grupo ou uma topologia) e a relação de equivalência ∼ ∼ {displaystyle ,sim ,} é compatível com esta estrutura, o conjunto quociente muitas vezes herda uma estrutura semelhante do seu conjunto pai. Exemplos incluem espaços quocientes em álgebra linear, espaços quocientes em topologia, grupos quocientes, espaços homogêneos, anéis quocientes, monoides quocientes e categorias de quocientes.
Exemplos
- Se X- Sim. é o conjunto de todos os carros, e ∼ ∼ {displaystyle ,sim ,} é a relação de equivalência "tem a mesma cor que", então uma classe de equivalência particular consistia em todos os carros verdes, e X/∼ ∼ {displaystyle X/{sim }} poderia ser naturalmente identificado com o conjunto de todas as cores do carro.
- Vamos. X- Sim. ser o conjunto de todos os retângulos em um avião, e ∼ ∼ {displaystyle ,sim ,} a relação de equivalência "tem a mesma área que", então para cada número real positivo A,Não. A, haverá uma classe de equivalência de todos os retângulos que têm área A.Não. A.
- Considere a relação de equivalência modulo 2 no conjunto de inteiros, Z.,{displaystyle mathbb {Z}} tal que x∼ ∼ Sim.- Sim. se e somente se a diferença deles x- Sim. - Sim. Sim.- Sim. é um número uniforme. Esta relação dá origem a exatamente duas classes de equivalência: uma classe consiste em todos os números pares, e a outra classe consiste em todos os números ímpares. Usando suportes quadrados em torno de um membro da classe para denotar uma classe de equivalência sob esta relação, Não.7],Não.9],[7],[9],} e Não.1]Não. [1] todos representam o mesmo elemento de Z./∼ ∼ .{displaystyle mathbb {Z} /{sim }.}
- Vamos. X- Sim. ser o conjunto de pares ordenados de inteiros (um,b))(a,b)} com não zero b),Não. e definir uma relação de equivalência ∼ ∼ {displaystyle ,sim ,} sobre X- Sim. tal que (um,b))∼ ∼ (c,D)(a,b)sim (c,d)} se e somente se umD= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b)c,Não. então a classe de equivalência do par (um,b))(a,b)} pode ser identificado com o número racional um/b),- Sim. e esta relação de equivalência e suas classes de equivalência podem ser usadas para dar uma definição formal do conjunto de números racionais. A mesma construção pode ser generalizada para o campo de frações de qualquer domínio integral.
- Se X- Sim. consiste em todas as linhas em, digamos, o plano euclidiano, e L∼ ∼ MNão. Lsim M significa que LNão. L. e MNão. são linhas paralelas, então o conjunto de linhas que são paralelas uns aos outros formam uma classe de equivalência, enquanto uma linha é considerada paralela a si mesmo. Nesta situação, cada classe de equivalência determina um ponto no infinito.
Definição e notação
Uma relação de equivalência em um conjunto X- Sim. é uma relação binária ∼ ∼ {displaystyle ,sim ,} sobre X- Sim. satisfazendo as três propriedades:
- um∼ ∼ um- Sim. para todos um∈ ∈ X- Sim. (reflexividade),
- um∼ ∼ b)- Sim. implica b)∼ ∼ umNão. para todos um,b)∈ ∈ X- Sim. (simetria),
- se um∼ ∼ b)- Sim. e b)∼ ∼ cNão. então um∼ ∼ cNão. para todos um,b),c∈ ∈ X- Sim. (transitividade).
A classe de equivalência de um elemento umNão. é muitas vezes denotado Não.um]Não. ou Não.um]∼ ∼ ,Não. e é definido como o conjunto (x∈ ∈ X:um∼ ∼ x?{displaystyle {xin X:asim x}} de elementos que estão relacionados umNão. por∼ ∼ .{displaystyle ,sim.} A palavra "classe" no termo "classe de equivalência" pode geralmente ser considerada como sinônimo de "set", embora algumas classes de equivalência não sejam conjuntos, mas classes apropriadas. Por exemplo, "ser isomorfo" é uma relação de equivalência em grupos, e as classes de equivalência, chamadas classes de isomorfismo, não são conjuntos.
O conjunto de todas as classes de equivalência em X- Sim. com relação a uma relação de equivalência RNão. R. é denotado como X/R,{displaystyle X/R,} e é chamado X- Sim. Modulo RNão. R. (ou o conjunto de citações de X- Sim. por RNão. R.). O mapa surjetivo x↦ ↦ Não.x]{displaystyle xmapsto [x]} a partir de X- Sim. sobre X/R,{displaystyle X/R,} que mapeia cada elemento para sua classe de equivalência, é chamado de surjecção canônicaou o projeção canônica.
Cada elemento de uma classe de equivalência caracteriza a classe, e pode ser usado para representação É. Quando tal elemento é escolhido, é chamado de representante da classe. A escolha de um representante em cada classe define uma injeção de X/R- Sim. para X. Desde a sua composição com a surjeção canônica é a identidade de X/R,{displaystyle X/R,} tal injeção é chamada de uma seção, ao usar a terminologia da teoria da categoria.
Às vezes, há uma seção que é mais "natural" do que os outros. Neste caso, os representantes são chamados representantes canônicos. Por exemplo, em aritmética modular, para cada inteiro m maior do que 1, o modulo de congruência m é uma relação de equivalência nos inteiros, para os quais dois inteiros um e b) são equivalentes — neste caso, um diz Congruente — se m divide um- Sim. - Sim. b);- Sim. isto é denotado um)) b)(modm).{textstyle aequiv b{pmod {m}}} Cada classe contém um inteiro não negativo único menor do que m,- Sim. e estes inteiros são os representantes canônicos.
O uso de representantes para representar classes permite evitar considerar explicitamente classes como conjuntos. Neste caso, a surjeção canônica que mapeia um elemento para sua classe é substituída pela função que mapeia um elemento para o representante de sua classe. No exemplo anterior, esta função é denotada ummodm,{displaystyle a{bmod {m}},} e produz o restante da divisão euclidiana um por m.
Propriedades
Cada elemento xNão. de X- Sim. é um membro da classe de equivalência Não.x].- Sim. Cada duas classes de equivalência Não.x][x] e Não.Sim.]- Sim. são iguais ou disjuntos. Portanto, o conjunto de todas as classes de equivalência de X- Sim. forma uma partição de X- Sim.: cada elemento X- Sim. pertence a uma única classe de equivalência. Por outro lado, cada partição de X- Sim. vem de uma relação de equivalência desta forma, segundo a qual x∼ ∼ Sim.- Sim. se e somente se xNão. e Sim.- Sim. pertencem ao mesmo conjunto da partição.
Resulta das propriedades de uma relação de equivalência que
Em outras palavras, se ∼ ∼ {displaystyle ,sim ,} é uma relação de equivalência em um conjunto X,Não. X, e xNão. e Sim.- Sim. são dois elementos de X,Não. X, então estas declarações são equivalentes:
- x∼ ∼ Sim.- Sim.
- Não.x]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.Sim.]- Sim.
- Não.x]─ ─ Não.Sim.]≠ ≠ ∅ ∅ .{displaystyle [x]cap [y]neq emptyset.}
Representação gráfica
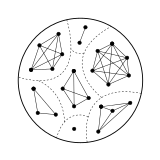
Um gráfico não direcionado pode estar associado a qualquer relação simétrica em um conjunto X,Não. X, onde os vértices são os elementos de X,Não. X, e dois vértices SNão. e )Não. são unidos se e somente se S∼ ∼ ).Não. Entre esses gráficos estão os gráficos das relações de equivalência; eles são caracterizados como os gráficos tais que os componentes conectados são cliques.
Invariantes
Se ∼ ∼ {displaystyle ,sim ,} é uma relação de equivalência X,Não. X, e P(x)(x)} é uma propriedade de elementos de X- Sim. tal que sempre x∼ ∼ Sim.,{displaystyle xsim y,} P(x)(x)} é verdade se P(Sim.)Não. é verdade, então a propriedade PNão. P. é dito ser um invariante de ∼ ∼ ,{displaystyle ,sim ,} ou bem definido sob a relação ∼ ∼ .{displaystyle ,sim.}
Um caso particular frequente ocorre quando fNão. é uma função de X- Sim. para outro conjunto YNão. Sim.; se f(x1)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =f(x2){displaystyle fleft(x_{1}right)=fleft(x_{2}right)} sempre x1∼ ∼ x2,{displaystyle x_{1}sim x_{2},} então fNão. é dito para ser classe invariável sob ∼ ∼ ,{displaystyle ,sim ,} ou simplesmente invariante sob ∼ ∼ .{displaystyle ,sim.} Isso ocorre, por exemplo, na teoria dos caracteres de grupos finitos. Alguns autores usam "compatível com ∼ ∼ {displaystyle ,sim ,}"ou apenas "respeitos ∼ ∼ {displaystyle ,sim ,}" em vez de "invariante sob ∼ ∼ {displaystyle ,sim ,}".
Qualquer função f:X→ → Y{displaystyle f:Xto Sim. o classe invariável sob ∼ ∼ ,{displaystyle ,sim ,} segundo o qual x1∼ ∼ x2{displaystyle x_{1}sim x_{2}} se e somente se f(x1)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =f(x2).{displaystyle fleft(x_{1}right)=fleft(x_{2}right). ? A classe de equivalência xNão. é o conjunto de todos os elementos em X- Sim. que são mapeados para f(x),{displaystyle f(x),} isto é, a classe Não.x][x] é a imagem inversa de f(x).{displaystyle f(x).} Esta relação de equivalência é conhecida como kernel do f.Não.
Mais geralmente, uma função pode mapear argumentos equivalentes (sob uma relação de equivalência ∼ ∼ X{displaystyle sim _{X}} sobre X- Sim.) a valores equivalentes (sob relação de equivalência ∼ ∼ Y{displaystyle sim _{Y}} sobre YNão. Sim.). Tal função é um morfismo de conjuntos equipados com uma relação de equivalência.
Espaço quociente na topologia
Na topologia, um espaço quociente é um espaço topológico formado no conjunto de classes de equivalência de uma relação de equivalência em um espaço topológico, usando a topologia do espaço original para criar a topologia no conjunto de classes de equivalência.
Na álgebra abstrata, as relações de congruência no conjunto subjacente de uma álgebra permitem que a álgebra induza uma álgebra nas classes de equivalência da relação, chamada álgebra de quociente. Na álgebra linear, um espaço quociente é um espaço vetorial formado por um grupo quociente, onde o homomorfismo quociente é um mapa linear. Por extensão, na álgebra abstrata, o termo espaço quociente pode ser usado para módulos quocientes, anéis quocientes, grupos quocientes ou qualquer álgebra quociente. No entanto, o uso do termo para os casos mais gerais também pode ser feito por analogia com as órbitas de uma ação de grupo.
As órbitas de uma ação de grupo em um conjunto podem ser chamadas de espaço quociente da ação no conjunto, particularmente quando as órbitas da ação de grupo são os co-conjuntos corretos de um subgrupo de um grupo, que surgem da ação de o subgrupo no grupo por translações à esquerda ou, respectivamente, os co-conjuntos à esquerda como órbitas sob a translação à direita.
Um subgrupo normal de um grupo topológico, atuando no grupo por ação de translação, é um espaço quociente nos sentidos de topologia, álgebra abstrata e ações de grupo simultaneamente.
Embora o termo possa ser usado para o conjunto de classes de equivalência de qualquer relação de equivalência, possivelmente com mais estrutura, a intenção de usar o termo é geralmente comparar esse tipo de relação de equivalência em um conjunto X,Não. X, ou para uma relação de equivalência que induz alguma estrutura no conjunto de classes de equivalência de uma estrutura do mesmo tipo em X,Não. X, ou para as órbitas de uma ação de grupo. Tanto o sentido de uma estrutura preservada por uma relação de equivalência, como o estudo de invariantes sob ações de grupo, levam à definição de invariantes de relações de equivalência acima.
Contenido relacionado
Carl Friedrich Gauss
Integral elíptica
Função





![{displaystyle [a],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c16e3f39e424d6841ded4f27ebe110875a026c21)












![{displaystyle [7],[9],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/925eb1a9c42148a98f32d5b4c89ea765e57f5381)
![[1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/83021ecdd7307a04dbb7873affcaac031e7e935a)

















![[a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea82bc70a8e322f13a3c4e5b9d5d69e8ef097ad8)
![{displaystyle [a]_{sim },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa2d19f566f09441725f2c7df83961e8fb7aff40)




![{displaystyle xmapsto [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a07b95c49afdb5a84f26120657148e94c94a69be)






![{displaystyle [x].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00df149bf9dc9b370aecd7bec8c108b37a846117)
![[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
![[y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f637a17dac262ee0fc8d58e31d08ca3ebe5a0fed)

![{displaystyle [x]=[y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7d2321ddf22afae59b915931fe5e725e9de26e5)

![[x]=[y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c34866e2a1216182b168dc1e272b0b02f1aab3a)
![[x]cap [y]neq emptyset.](https://wikimedia.org/api/rest_v1/media/math/render/svg/2446e8a76d1e403fff2ee153d5dddef4cf1678ce)