Círculo

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Curva simples da geometria euclidiana

A círculo círculo é uma forma que consiste em todos os pontos em um plano que estão a uma dada distância de um determinado ponto, o centro. Equivalentemente, é a curva traçada por um ponto que se move em um plano para que sua distância de um determinado ponto é constante. A distância entre qualquer ponto do círculo e o centro é chamado de raio. Normalmente, o raio é necessário para ser um número positivo. Um círculo com $r=0$ (um único ponto) é um caso degenerado. Este artigo trata-se de círculos na geometria euclidiana, e, em particular, do plano euclidiano, exceto onde o contrário se observa.

Especificamente, um círculo é uma curva fechada simples que divide o plano em duas regiões: uma interior e uma exterior. No uso diário, o termo "círculo" pode ser usado indistintamente para se referir ao limite da figura ou à figura inteira, incluindo seu interior; no uso técnico estrito, o círculo é apenas o limite e toda a figura é chamada de disco.

Um círculo também pode ser definido como um tipo especial de elipse em que os dois focos são coincidentes, a excentricidade é 0 e os semi-eixos maiores e semi-menores são iguais; ou a forma bidimensional que abrange a maior área por unidade de perímetro ao quadrado, usando cálculo de variações.

Definição de Euclides

Um círculo é uma figura plana limitada por uma linha curva, e tal que todas as linhas retas desenhadas de um certo ponto dentro dele para a linha delimitação, são iguais. A linha de amarração é chamada de sua circunferência e o ponto, seu centro.
—Euclid, Elementos, Livro I

Definição topológica

No campo da topologia, um círculo não se limita ao conceito geométrico, mas a todos os seus homeomorfismos. Dois círculos topológicos são equivalentes se um pode ser transformado no outro por meio de uma deformação de R3 sobre si mesmo (conhecida como isotopia ambiente).

Terminologia

Annulus: um objeto em forma de anel, a região limitada por dois círculos concêntricos.
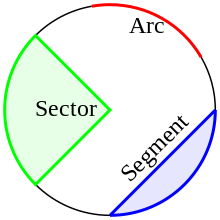
Arco: qualquer parte conectada de um círculo. Especificar dois pontos finais de um arco e um centro permite dois arcos que juntos compõem um círculo completo.
Centro: o ponto equidistante de todos os pontos no círculo.
Chord: um segmento de linha cujos endpoints estão sobre o círculo, dividindo assim um círculo em dois segmentos.
Circunferência: o comprimento de um circuito ao longo do círculo, ou a distância ao redor do círculo.
Diâmetro: um segmento de linha cujos pontos finais estão no círculo e que passa pelo centro; ou o comprimento de um segmento de linha. Esta é a maior distância entre dois pontos no círculo. É um caso especial de um acorde, ou seja, o acorde mais longo para um dado círculo, e seu comprimento é o dobro do comprimento de um raio.
Disco: a região do avião limitada por um círculo.
Lens: a região comum a (a interseção de) dois discos sobrepostos.
Passant: uma linha reta coplanar que não tem nenhum ponto em comum com o círculo.
Radius: um segmento de linha que une o centro de um círculo com qualquer ponto único no círculo em si; ou o comprimento de tal segmento, que é metade (o comprimento de) um diâmetro.
Setor: uma região delimitada por dois raios de comprimento igual com um centro comum e qualquer um dos dois arcos possíveis, determinado por este centro e os pontos finais do radii.
Segmento: uma região limitada por um acorde e um dos arcos conectando os pontos finais do acorde. O comprimento do acorde impõe um limite inferior no diâmetro de possíveis arcos. Às vezes o termo segmento é utilizado apenas para regiões que não contenham o centro do círculo ao qual pertence o seu arco.
Secant: um acorde estendido, uma linha reta coplanar, intersetando um círculo em dois pontos.
Semicírculo: um dos dois arcos possíveis determinados pelos pontos finais de um diâmetro, tomando seu ponto médio como centro. No uso comum não técnico, pode significar o interior da região bidimensional limitada por um diâmetro e um de seus arcos, que é tecnicamente chamado de meio-disco. Um meio-disco é um caso especial de um segmento, ou seja, o maior.
Tangente: uma linha reta coplanar que tem um único ponto em comum com um círculo ("toca o círculo neste ponto").

Todas as regiões especificadas podem ser consideradas como abertas, ou seja, não contendo seus limites, ou como fechadas, incluindo seus respectivos limites.

Chord, secant, tangente, raio e diâmetro

Arco, setor e segmento

História

A bússola neste manuscrito do século XIII é um símbolo do ato de Criação de Deus. Observe também a forma circular do halo.

A palavra círculo deriva do grego κίρκος/κύκλος (kirkos/kuklos), uma metátese do grego homérico κρίκος (krikos), que significa "arco" ou "anel". As origens das palavras circo e circuito estão intimamente relacionadas.

Seda circular com imagens mongóis

Círculos em um velho desenho astronômico árabe.

O círculo é conhecido desde antes do início da história registrada. Círculos naturais teriam sido observados, como a Lua, o Sol e um pequeno caule de planta soprando ao vento na areia, que forma um círculo na areia. O círculo é a base para a roda, que, com invenções relacionadas, como as engrenagens, possibilita grande parte do maquinário moderno. Na matemática, o estudo do círculo ajudou a inspirar o desenvolvimento da geometria, astronomia e cálculo.

A ciência primitiva, particularmente geometria, astrologia e astronomia, estava ligada ao divino para a maioria dos estudiosos medievais, e muitos acreditavam que havia algo intrinsecamente "divino" ou "perfeito" que podem ser encontrados em círculos.

Alguns destaques na história do círculo são:

1700 a.C. – O papiro Rhind dá um método para encontrar a área de um campo circular. O resultado corresponde a 256./81 (3.16049...) como um valor aproximado de π.

Torre de Tughrul de dentro

300 a.C. – O livro 3 dos Elementos de Euclides lida com as propriedades dos círculos.
Na Sétima Carta de Platão há uma definição detalhada e explicação do círculo. Platão explica o círculo perfeito, e como é diferente de qualquer desenho, palavras, definição ou explicação.
1880 CE – Lindemann prova que $D$ é transcendental, efetivamente estabelecendo o problema milênio-velho de squaring o círculo.

Resultados analíticos

Circunferência

A razão entre a circunferência de um círculo e seu diâmetro é $π$ (pi), uma constante irracional aproximadamente igual para 3.141592654. Assim, a circunferência C está relacionada ao raio r e ao diâmetro d por:

C=2pi r=pi d.,

Área fechada

Área fechada por um círculo =

D

× área do quadrado sombreado

Como provado por Arquimedes, em sua Medição de um Círculo, a área delimitada por um círculo é igual à de um triângulo cuja base tem o comprimento da circunferência do círculo e cuja altura é igual à circunferência do círculo. s raio, que resulta em $π$ multiplicado pelo raio ao quadrado:

mathrm {Area} =pi r^{2}.,

Equivalentemente, denotando diâmetro por d,

mathrm {Area} ={frac {pi d^{2}}{4}}approx 0{.}7854d^{2},

ou seja, aproximadamente 79% do quadrado circunscrito (cujo lado tem comprimento d).

O círculo é a curva plana que abrange a área máxima para um determinado comprimento de arco. Isso relaciona o círculo a um problema no cálculo das variações, ou seja, a desigualdade isoperimétrica.

Equações

Coordenadas cartesianas

Círculo de raio R= 1, centro (um,b)) = (1.2, −0.5)

Equação de um círculo

Em um sistema de coordenadas cartesianas x–y, o círculo com coordenadas centrais (a, b) e o raio r é o conjunto de todos os pontos (x, y) tais que

{displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}.}

Esta equação, conhecida como equação do círculo, decorre do teorema de Pitágoras aplicado a qualquer ponto do círculo: como mostrado no diagrama adjacente, o raio é a hipotenusa de uma triângulo angular cujos outros lados são de comprimento |x − a| e |y − b|. Se o círculo estiver centrado na origem (0, 0), a equação será simplificada para

{displaystyle x^{2}+y^{2}=r^{2}.}

Forma paramétrica

A equação pode ser escrita na forma paramétrica usando as funções trigonométricas seno e cosseno como

{displaystyle x=a+r,cos t,}

{displaystyle y=b+r,sin t,}

onde t é uma variável paramétrica no intervalo de 0 a 2 $π$ , interpretado geometricamente como o ângulo que o raio de (a, b) para (x, y) faz com o positivo x eixo.

Uma parametrização alternativa do círculo é

{displaystyle x=a+r{frac {1-t^{2}}{1+t^{2}}},}

{displaystyle y=b+r{frac {2t}{1+t^{2}}}.}

Nesta parametrização, a razão de t para r pode ser interpretada geometricamente como a projeção estereográfica da linha que passa pelo centro paralelo ao x eixo (consulte Substituição de meio-ângulo tangente). No entanto, esta parametrização funciona apenas se t for feito para abranger não apenas todos os reais, mas também um ponto no infinito; caso contrário, o ponto mais à esquerda do círculo seria omitido.

Forma de 3 pontos

A equação do círculo determinada por três pontos ${displaystyle (x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})}$ não em uma linha é obtido por uma conversão da forma de 3 pontos de uma equação de círculo:

{displaystyle {frac {({color {green}x}-x_{1})({color {green}x}-x_{2})+({color {red}y}-y_{1})({color {red}y}-y_{2})}{({color {red}y}-y_{1})({color {green}x}-x_{2})-({color {red}y}-y_{2})({color {green}x}-x_{1})}}={frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}.}

Forma homogênea

Em coordenadas homogêneas, cada seção cônica com a equação de um círculo tem a forma

{displaystyle x^{2}+y^{2}-2axz-2byz+cz^{2}=0.}

Pode-se provar que uma seção cônica é um círculo exatamente quando contém (quando estendida ao plano projetivo complexo) os pontos I(1: i: 0) e J(1: −i: 0). Esses pontos são chamados de pontos circulares no infinito.

Coordenadas polares

Em coordenadas polares, a equação de um círculo é

{displaystyle r^{2}-2rr_{0}cos(theta -phi)+r_{0}^{2}=a^{2},}

Onde? um é o raio do círculo, $(r,theta)$ são as coordenadas polares de um ponto genérico no círculo, e $(r_0, phi)$ são as coordenadas polares do centro do círculo (i.e., R₀ é a distância da origem ao centro do círculo, e φ é o ângulo anti-horário do positivo xeixo para a linha que liga a origem ao centro do círculo). Para um círculo centrado na origem, isto é, R₀ = 0, isto reduz a R = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um. Quando R₀ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um, ou quando a origem está no círculo, a equação se torna

{displaystyle r=2acos(theta -phi).}

No caso geral, a equação pode ser resolvida para r, dando

{displaystyle r=r_{0}cos(theta -phi)pm {sqrt {a^{2}-r_{0}^{2}sin ^{2}(theta -phi)}}.}

Observe que sem o sinal ±, a equação em alguns casos descreveria apenas meio círculo.

Plano complexo

No plano complexo, um círculo com centro em c e raio r tem a equação

{displaystyle |z-c|=r.}

Na forma paramétrica, isso pode ser escrito como

{displaystyle z=re^{it}+c.}

A equação ligeiramente generalizada

pzoverline{z} + gz + overline{gz} = q

para real p, q e complexo g às vezes é chamado de círculo generalizado. Isso se torna a equação acima para um círculo com ${displaystyle p=1, g=-{overline {c}}, q=r^{2}-|c|^{2}}$ , desde ${displaystyle |z-c|^{2}=z{overline {z}}-{overline {c}}z-c{overline {z}}+c{overline {c}}}$ . Nem todos os círculos generalizados são realmente círculos: um círculo generalizado é um círculo (verdadeiro) ou uma linha.

Linhas tangentes

A reta tangente através de um ponto P no círculo é perpendicular ao diâmetro que passa por P. Se P = (x₁, y₁) e o círculo tem centro (a, b) e raio r, então a linha tangente é perpendicular à linha de (a , b) para (x₁, y₁), então tem a forma (x₁ − a)x + (y₁ – b)y = c. Avaliando em (x₁, y₁) determina o valor de c, e o resultado é que a equação da tangente é

{displaystyle (x_{1}-a)x+(y_{1}-b)y=(x_{1}-a)x_{1}+(y_{1}-b)y_{1},}

{displaystyle (x_{1}-a)(x-a)+(y_{1}-b)(y-b)=r^{2}.}

Se y₁ ≠ b, então a inclinação desta linha é

{displaystyle {frac {dy}{dx}}=-{frac {x_{1}-a}{y_{1}-b}}.}

Isso também pode ser encontrado usando diferenciação implícita.

Quando o centro do círculo está na origem, a equação da reta tangente se torna

{displaystyle x_{1}x+y_{1}y=r^{2},}

e sua inclinação é

frac{dy}{dx} = -frac{x_1}{y_1}.

Propriedades

O círculo é a forma com a maior área para um determinado comprimento de perímetro (veja Isoperimetric inequality).
O círculo é uma forma altamente simétrica: cada linha através do centro forma uma linha de simetria de reflexão, e tem simetria rotacional em torno do centro para cada ângulo. Seu grupo de simetria é o grupo ortogonal O(2,R). O grupo de rotações sozinho é o grupo círculo T.
Todos os círculos são semelhantes.
- Uma circunferência círculo e raio são proporcionais.
- A área fechada e a praça do seu raio são proporcionais.
- As constantes da proporcionalidade são 2 $D$ e $D$ respectivamente.
O círculo que está centrado na origem com o raio 1 chama-se o círculo da unidade.
- Pensado como um grande círculo da esfera unitária, torna-se o círculo Riemannian.
Através de três pontos, nem todos na mesma linha, existe um círculo único. Nas coordenadas cartesianas, é possível dar fórmulas explícitas para as coordenadas do centro do círculo e do raio em termos das coordenadas dos três pontos dados. Ver circuncírculo.

Acorde

Os acordes são equidistantes do centro de um círculo se e somente se forem iguais em comprimento.
O bissetor perpendicular de um acorde passa pelo centro de um círculo; declarações equivalentes decorrentes da singularidade do bissetor perpendicular são:
- Uma linha perpendicular do centro de um círculo bisecta o acorde.
- O segmento de linha através do centro de bisectar um acorde é perpendicular ao acorde.
Se um ângulo central e um ângulo inscrito de um círculo são subtendidos pelo mesmo acorde e no mesmo lado do acorde, então o ângulo central é o dobro do ângulo inscrito.
Se dois ângulos são inscritos no mesmo acorde e no mesmo lado do acorde, então eles são iguais.
Se dois ângulos são inscritos no mesmo acorde e em lados opostos do acorde, então eles são complementares.
- Para um quadrilateral cíclico, o ângulo exterior é igual ao ângulo oposto interior.
Um ângulo inscrito subtendido por um diâmetro é um ângulo direito (veja o teorema de Thales).
O diâmetro é o acorde mais longo do círculo.
- Entre todos os círculos com um acorde AB em comum, o círculo com raio mínimo é aquele com diâmetro AB.
Se a interseção de quaisquer dois acordes divide um acorde em comprimentos um e b) e divide o outro acorde em comprimentos c e D, então A = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = cd.
Se a interseção de quaisquer dois acordes perpendiculares divide um acorde em comprimentos um e b) e divide o outro acorde em comprimentos c e D, então um² + b)² + c² + D² é igual ao quadrado do diâmetro.
A soma dos comprimentos quadrados de quaisquer dois acordes que se cruzam em ângulos retos em um determinado ponto é a mesma que a de qualquer outro dois acordes perpendiculares que se cruzam no mesmo ponto e é dada por 8R² - 4p², onde R é o raio do círculo, e p é a distância do ponto central para o ponto de interseção.
A distância de um ponto no círculo a um determinado acorde vezes o diâmetro do círculo é igual ao produto das distâncias do ponto às extremidades do acorde.

Tangente

Uma linha desenhada perpendicular a um raio através do ponto final do raio deitado no círculo é um tangente ao círculo.
Uma linha desenhada perpendicular a um tangente através do ponto de contato com um círculo passa pelo centro do círculo.
Dois tangentes sempre podem ser atraídos para um círculo de qualquer ponto fora do círculo, e esses tangentes são iguais em comprimento.
Se um tangente A e um tangente em B intersect no ponto exterior P, então denotando o centro como O, os ângulosBOA eBPA são complementares.
Se ANÚNCIO é tangente ao círculo em A e se AQ é um acorde do círculo, então ?DAQ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 1/2(em inglês)AQ).

Teoremas

teorema de secanto

O teorema de acordes afirma que se dois acordes, CD e EB, intersecção A, então ACÇÃO × ANÚNCIO = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = AB × AE.
Se dois secantes, AE e ANÚNCIO, também cortar o círculo em B e C respectivamente, então ACÇÃO × ANÚNCIO = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = AB × AE (corollário do teorema do acorde).
Um tangente pode ser considerado um caso limitante de um secante cujas extremidades são coincidentes. Se um tangente de um ponto externo A encontra o círculo em F e um secante do ponto externo A encontra o círculo em C e D respectivamente, então AF² = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ACÇÃO × ANÚNCIO (teorema tangent-secant).
O ângulo entre um acorde e o tangente em um de seus pontos finais é igual a uma metade do ângulo subtendido no centro do círculo, no lado oposto do acorde (ângulo de acorde tangent).
Se o ângulo subtendido pelo acorde no centro for 90°, então Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = R √2, onde Eu... é o comprimento do acorde, e R é o raio do círculo.
Se dois secantes são inscritos no círculo como mostrado à direita, então a medição do ângulo A é igual a metade da diferença das medidas dos arcos fechados ( ${displaystyle {overset {frown }{DE}}}$ e ${displaystyle {overset {frown }{BC}}}$ ). Isso é, ${displaystyle 2angle {CAB}=angle {DOE}-angle {BOC}}$ , onde O é o centro do círculo (teorema secant-secant).

Ângulos inscritos

Teorema de ângulo inscrito

Um ângulo inscrito (exemplos são os ângulos azuis e verdes na figura) é exatamente a metade do ângulo central correspondente (vermelho). Portanto, todos os ângulos inscritos que subentendem o mesmo arco (rosa) são iguais. Os ângulos inscritos no arco (marrom) são suplementares. Em particular, todo ângulo inscrito que subtende um diâmetro é um ângulo reto (uma vez que o ângulo central é de 180°).

Sagitta

A sagitta é o segmento vertical.

A sagitta (também conhecida como versine) é um segmento de linha traçado perpendicularmente a uma corda, entre o ponto médio dessa corda e o arco do círculo.

Dado o comprimento y de uma corda e o comprimento x da sagitta, o teorema de Pitágoras pode ser usado para calcular o raio do círculo único que caberá ao redor as duas linhas:

{displaystyle r={frac {y^{2}}{8x}}+{frac {x}{2}}.}

Outra prova deste resultado, que se baseia apenas em duas propriedades de acorde fornecidas acima, é a seguinte. Dada uma corda de comprimento y e com sagitta de comprimento x, como a sagitta intercepta o ponto médio da corda, sabemos que é uma parte de um diâmetro do círculo. Como o diâmetro é o dobro do raio, o "ausente" parte do diâmetro é (2r − x) de comprimento. Usando o fato de que uma parte de um acorde vezes a outra parte é igual ao mesmo produto obtido ao longo de um acorde que intercepta o primeiro acorde, descobrimos que (2r − x)x = (y / 2)². Resolvendo para r, encontramos o resultado desejado.

Construções com régua e compasso

Existem muitas construções com régua e compasso que resultam em círculos.

O mais simples e básico é a construção dado o centro do círculo e um ponto no círculo. Coloque a perna fixa do compasso no ponto central, a perna móvel no ponto do círculo e gire o compasso.

Construção com determinado diâmetro

Construir o ponto médio $M$ do diâmetro.
Construir o círculo com centro $M$ passando por um dos pontos finais do diâmetro (ele também passará pelo outro ponto final).

Construa um círculo através dos pontos A, B e C, encontrando os bissetores perpendiculares (vermelho) dos lados do triângulo (azul). Apenas dois dos três bissetores são necessários para encontrar o centro.

Construção através de três pontos não colineares

Nomear os pontos $P$ , $Q$ e $R$ ,
Construir o bissetor perpendicular do segmento $PQ$ .
Construir o bissetor perpendicular do segmento $Relações públicas$ .
Etiqueta o ponto de interseção destes dois bissetores perpendiculares $M$ . (Eles se reúnem porque os pontos não são collineares).
Construir o círculo com centro $M$ passando por um dos pontos $P$ , $Q$ ou $R$ (também passará pelos outros dois pontos).

Círculo de Apolônio

Definição de um círculo: D₁/D₂ constante constante

Apolônio de Perga mostrou que um círculo também pode ser definido como o conjunto de pontos em um plano tendo uma razão constante (diferente de 1) de distâncias para dois focos fixos, A e B. (O conjunto de pontos onde as distâncias são iguais é a bissetriz perpendicular do segmento AB, uma linha.) Às vezes, diz-se que esse círculo é desenhado cerca de dois pontos.

A prova está em duas partes. Primeiro, deve-se provar que, dados dois focos A e B e uma razão de distâncias, qualquer ponto P que satisfaça a razão de distâncias deve cair em um determinado círculo. Seja C outro ponto, também satisfazendo a razão e situado no segmento AB. Pelo teorema da bissetriz do ângulo, o segmento de reta PC irá bissecionar o ângulo interno APB, pois os segmentos são semelhantes:

frac{AP}{BP} = frac{AC}{BC}.

Analogicamente, um segmento de reta PD passando por algum ponto D em AB estendido bissecta o ângulo externo correspondente BPQ onde Q está em AP estendido. Como os ângulos interno e externo somam 180 graus, o ângulo CPD é exatamente 90 graus; isto é, um ângulo reto. O conjunto de pontos P tal que o ângulo CPD é um ângulo reto forma um círculo, do qual CD é um diâmetro.

Segundo, veja uma prova de que cada ponto no círculo indicado satisfaz a razão dada.

Proporções cruzadas

Uma propriedade estreitamente relacionada dos círculos envolve a geometria da razão cruzada de pontos no plano complexo. Se A, B e C forem como acima, então o círculo de Apolônio para esses três pontos é a coleção de pontos P para o qual o valor absoluto da razão cruzada é igual a um:

{displaystyle {big |}[A,B;C,P]{big |}=1.}

Em outras palavras, P é um ponto no círculo de Apolônio se e somente se a razão cruzada [A, B; C, P] está no círculo unitário no plano complexo.

Círculos generalizados

Se C é o ponto médio do segmento AB, então a coleção de pontos P satisfaz a condição de Apolônio

frac{|AP|}{|BP|} = frac{|AC|}{|BC|}

não é um círculo, mas sim uma linha.

Assim, se A, B e C são dados pontos distintos no plano, então o lugar geométrico dos pontos P que satisfaz a equação acima é chamado de "círculo generalizado." Pode ser um círculo verdadeiro ou uma linha. Nesse sentido, uma linha é um círculo generalizado de raio infinito.

Inscrição em ou circunscrição sobre outras figuras

Em todo triângulo, um único círculo, chamado círculo interno, pode ser inscrito de modo que seja tangente a cada um dos três lados do triângulo.

Em todo triângulo, um único círculo, chamado circuncírculo, pode ser circunscrito de modo que passe por cada um dos três vértices do triângulo.

Um polígono tangencial, como um quadrilátero tangencial, é qualquer polígono convexo dentro do qual pode ser inscrito um círculo tangente a cada lado do polígono. Todo polígono regular e todo triângulo é um polígono tangencial.

Um polígono cíclico é qualquer polígono convexo sobre o qual um círculo pode ser circunscrito, passando por cada vértice. Um exemplo bem estudado é o quadrilátero cíclico. Todo polígono regular e todo triângulo é um polígono cíclico. Um polígono que é cíclico e tangencial é chamado de polígono bicêntrico.

Uma hipociclóide é uma curva que é inscrita em um determinado círculo traçando um ponto fixo em um círculo menor que rola dentro e é tangente ao círculo dado.

Caso limitante de outras figuras

O círculo pode ser visto como um caso limite de cada uma das várias outras figuras:

Um oval cartesiano é um conjunto de pontos tais que uma soma ponderada das distâncias de qualquer um de seus pontos para dois pontos fixos (foci) é uma constante. Uma elipse é o caso em que os pesos são iguais. Um círculo é um elipse com uma excentricidade de zero, o que significa que os dois foci coincidem uns com os outros como o centro do círculo. Um círculo também é um caso especial diferente de um oval cartesiano em que um dos pesos é zero.
Um superellipse tem uma equação da forma $left|frac{x}{a}right|^n! + left|frac{y}{b}right|^n! = 1$ para positivo um, b)e n. Um supercirculo tem b) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um. Um círculo é o caso especial de um supercírculo em que n = 2.
Um oval de Cassini é um conjunto de pontos que o produto das distâncias de qualquer um de seus pontos para dois pontos fixos é uma constante. Quando os dois pontos fixos coincidem, um círculo resulta.
Uma curva de largura constante é uma figura cuja largura, definida como a distância perpendicular entre duas linhas paralelas distintas cada uma intersetando seu limite em um único ponto, é a mesma independentemente da direção dessas duas linhas paralelas. O círculo é o exemplo mais simples deste tipo de figura.

Noutras p-normas

Ilustrações de círculos unitários (ver também superellipse) em diferentes

p

-normas (todo o vetor da origem ao círculo unitário tem um comprimento de um, o comprimento sendo calculado com forma de comprimento do correspondente

p

Definindo um círculo como o conjunto de pontos com uma distância fixa de um ponto, diferentes formas podem ser consideradas círculos sob diferentes definições de distância. Na norma p, a distância é determinada por

{displaystyle left|xright|_{p}=left(|x_{1}|^{p}+|x_{2}|^{p}+dotsb +|x_{n}|^{p}right)^{1/p}.}

Na geometria euclidiana, p = 2, dando o familiar

{displaystyle left|xright|_{2}={sqrt {|x_{1}|^{2}+|x_{2}|^{2}+dotsb +|x_{n}|^{2}}}.}

Na geometria do táxi, p = 1. Os círculos de Taxicab são quadrados com lados orientados a um ângulo de 45° para os eixos de coordenadas. Enquanto cada lado teria comprimento $sqrt{2}r$ usando uma métrica Euclidiana, onde R é o raio do círculo, seu comprimento na geometria do táxi é 2R. Assim, a circunferência de um círculo é 8R. Assim, o valor de um analógico geométrico a $pi$ é 4 nesta geometria. A fórmula para o círculo de unidade na geometria do táxi é $|x|+|y|=1$ em coordenadas cartesianas e

r={frac {1}{|sin theta |+|cos theta |}}

em coordenadas polares.

Um círculo de raio 1 (usando esta distância) é a vizinhança de von Neumann de seu centro.

Um círculo de raio r para a distância Chebyshev (métrica L∞) em um plano também é um quadrado com comprimento lateral 2r paralelo aos eixos coordenados, então A distância planar de Chebyshev pode ser vista como equivalente por rotação e escala para a distância planar do táxi. No entanto, essa equivalência entre as métricas L₁ e L_∞ não se generaliza para dimensões superiores.

Locus da soma constante

Considere um conjunto finito de $n$ pontos no avião. O locus de pontos tal que a soma dos quadrados das distâncias aos pontos dados é constante é um círculo, cujo centro está no centroid dos pontos dados. Uma generalização para maiores potências de distâncias é obtida se abaixo $n$ aponta os vértices do polígono regular $P_{n}$ são levados. O locus de pontos tal que a soma do ${displaystyle (2m)}$ -o poder das distâncias $d_{i}$ aos vértices de um dado polígono regular com circunradius $R$ é constante é um círculo, se

nR^{2m}}" xmlns="http://www.w3.org/1998/Math/MathML">Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nDEu...2m>nR2m{displaystyle sum _{i=1}^{n}d_{i}^{2m}>nR^{2m}}nR^{2m}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0aba8e5893caef016f476abbc446aacbf8045c21" style="vertical-align: -3.005ex; width:16.211ex; height:6.843ex;"/>

, onde

m

=1,2,...,

n

-1;

cujo centro é o centroid do $P_{n}$ .

No caso do triângulo equilátero, os lugares geométricos das somas constantes da segunda e quarta potências são círculos, enquanto para o quadrado, os lugares geométricos são círculos das somas constantes da segunda, quarta e sexta potências. Para o pentágono regular, a soma constante das oitavas potências das distâncias será adicionada e assim por diante.

Quadratura do círculo

A quadratura do círculo é o problema, proposto pelos antigos geômetras, de construir um quadrado com a mesma área de um círculo dado usando apenas um número finito de passos com régua e compasso.

Em 1882, a tarefa provou ser impossível, como consequência do teorema de Lindemann–Weierstrass, que prova que pi ( $π$ ) é um número transcendental, em vez de um número irracional algébrico; ou seja, não é a raiz de nenhum polinômio com coeficientes racionais. Apesar da impossibilidade, este tópico continua a interessar aos entusiastas da pseudomatemática.

Significado na arte e simbolismo

Desde o tempo das primeiras civilizações conhecidas – como os assírios e antigos egípcios, aqueles no vale do Indo e ao longo do rio Amarelo na China, e as civilizações ocidentais da Grécia e Roma antigas durante a Antiguidade clássica – o círculo tem sido usado direta ou indiretamente na arte visual para transmitir a mensagem do artista e para expressar certas ideias. No entanto, as diferenças de visão de mundo (crenças e cultura) tiveram um grande impacto nas percepções dos artistas. Enquanto alguns enfatizavam o perímetro do círculo para demonstrar sua manifestação democrática, outros focavam em seu centro para simbolizar o conceito de unidade cósmica. Nas doutrinas místicas, o círculo simboliza principalmente a natureza infinita e cíclica da existência, mas nas tradições religiosas representa os corpos celestes e os espíritos divinos. O círculo significa muitos conceitos sagrados e espirituais, incluindo unidade, infinito, totalidade, universo, divindade, equilíbrio, estabilidade e perfeição, entre outros. Tais conceitos foram transmitidos em culturas em todo o mundo através do uso de símbolos, por exemplo, uma bússola, uma auréola, a vesica piscis e seus derivados (peixe, olho, auréola, mandorla, etc.), o ouroboros, a roda do Dharma, um arco-íris, mandalas, rosáceas e assim por diante.

Contenido relacionado

Más resultados...