Calorimetria

O primeiro mundo Calor de gelo, usado no inverno de 1782–83, por Antoine Lavoisier e Pierre-Simon Laplace, para determinar o calor envolvido em várias mudanças químicas; cálculos que foram baseados na descoberta prévia de Joseph Black de calor latente. Estas experiências marcam a fundação da termoquímica.

Snellen câmara de calorimetria direta, Universidade de Ottawa.

Carrinho metabólico indireto de calorimetria medindo o consumo de oxigênio e a produção de CO2 de um sujeito espontaneamente respiratório (método de diluição com capota).

Em química e termodinâmica, calorimetria (do latim calor 'calor' e grego μέτρον (metron) 'medida') é a ciência ou ato de medir mudanças em variáveis de estado de um corpo com a finalidade de derivar a transferência de calor associada a mudanças de seu estado devido, por exemplo, a reações químicas, mudanças físicas ou transições de fase sob restrições especificadas. A calorimetria é realizada com um calorímetro. O médico e cientista escocês Joseph Black, que foi o primeiro a reconhecer a distinção entre calor e temperatura, é considerado o fundador da ciência da calorimetria.

A calorimetria indireta calcula o calor que os organismos vivos produzem medindo sua produção de dióxido de carbono e resíduos de nitrogênio (frequentemente amônia em organismos aquáticos ou uréia em organismos terrestres) ou de seu consumo de oxigênio. Lavoisier observou em 1780 que a produção de calor pode ser prevista a partir do consumo de oxigênio dessa maneira, usando regressão múltipla. A teoria do orçamento dinâmico de energia explica por que esse procedimento é correto. O calor gerado por organismos vivos também pode ser medido por calorimetria direta, na qual todo o organismo é colocado dentro do calorímetro para a medição.

Um instrumento moderno amplamente utilizado é o calorímetro diferencial de varredura, um dispositivo que permite a obtenção de dados térmicos em pequenas quantidades de material. Envolve aquecer a amostra a uma taxa controlada e registrar o fluxo de calor para dentro ou para fora da amostra.

Cálculo calorimétrico clássico de calor

Casos com equação de estado diferenciável para um corpo de um componente

Cálculo clássico básico em relação ao volume

A calorimetria requer que um material de referência que muda de temperatura tenha propriedades constitutivas térmicas conhecidas. A regra clássica, reconhecida por Clausius e Kelvin, é que a pressão exercida pelo material calorimétrico é total e rapidamente determinada apenas por sua temperatura e volume; esta regra é para mudanças que não envolvem mudança de fase, como o derretimento do gelo. Existem muitos materiais que não obedecem a esta regra e, para eles, a fórmula atual da calorimetria clássica não fornece uma conta adequada. Aqui, assume-se que a regra clássica é válida para o material calorimétrico que está sendo usado, e as proposições são escritas matematicamente:

A resposta térmica do material calorimétrico é totalmente descrita por sua pressão pNão. como valor da sua função constitutiva p(V,T)} de apenas o volume VNão. V e a temperatura TNão. T.. Todos os incrementos estão aqui necessários para ser muito pequeno. Este cálculo refere-se a um domínio de volume e temperatura do corpo em que nenhuma mudança de fase ocorre, e há apenas uma fase presente. Uma suposição importante aqui é a continuidade das relações de propriedade. Uma análise diferente é necessária para a mudança de fase

Quando um pequeno incremento de calor é ganho por um corpo calorimétrico, com pequenos incrementos, δ δ V{displaystyle delta V } de seu volume, e δ δ T{displaystyle delta T. de sua temperatura, o incremento de calor, δ δ Q{displaystyle delta Q }, ganho pelo corpo do material calórico, é dado por

δ δ Q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =CT(V)(V,T)δ δ V+CV(T)(V,T)δ δ T{displaystyle delta Q =C_{T}^{(V)}(V,T),delta V,+,C_{V}^{(T)}(V,T),delta T}

onde

CT(V)(V,T){displaystyle C_{T}^{(V)}(V,T) } denota o calor latente em relação ao volume, do material calorimétrico em temperatura controlada constante TNão. T.. A pressão dos arredores sobre o material é ajustada instrumentalmente para impor uma mudança de volume escolhida, com volume inicial VNão. V. Para determinar este calor latente, a mudança de volume é efetivamente a quantidade instrumentalmente variada independentemente. Este calor latente não é um dos amplamente utilizados, mas é de interesse teórico ou conceitual.

CV(T)(V,T){displaystyle C_{V}^{(T)}(V,T) } denota a capacidade de calor, do material calorimétrico em volume constante fixo VNão. V, enquanto a pressão do material é permitida a variar livremente, com a temperatura inicial TNão. T.. A temperatura é forçada a mudar por exposição a um banho de calor adequado. É costume escrever CV(T)(V,T){displaystyle C_{V}^{(T)}(V,T) } simplesmente CV(V,T)Não. C_{V}(V,T) }, ou ainda mais brevemente CVNão. C_{V} }. Este calor latente é um dos dois amplamente utilizados.

O calor latente em relação ao volume é o calor necessário para incremento de unidade em volume a temperatura constante. Pode-se dizer que é 'medido ao longo de um isotérmico', e a pressão que os materiais exercem é permitida a variar livremente, de acordo com sua lei constitutiva. p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =p(V,T)}. Para um determinado material, pode ter um sinal positivo ou negativo ou excepcionalmente pode ser zero, e isso pode depender da temperatura, como faz para a água cerca de 4 C. O conceito de calor latente em relação ao volume foi talvez primeiro reconhecido por Joseph Black em 1762. O termo "calor de expansão" também é usado. O calor latente em relação ao volume também pode ser chamado de "energia latente em relação ao volume". Para todos esses usos de 'calor lactente', uma terminologia mais sistemática usa 'capacidade de calor latente'.

A capacidade térmica a volume constante é o calor necessário para o incremento unitário de temperatura a volume constante. Pode-se dizer que é 'medido ao longo de uma isocor' e, novamente, a pressão que o material exerce pode variar livremente. Tem sempre um sinal positivo. Isso significa que, para aumentar a temperatura de um corpo sem alterar seu volume, o calor deve ser fornecido a ele. Isso é consistente com a experiência comum.

Quantidades como δ δ Q{displaystyle delta Q } às vezes são chamados de "diferenciamentos de curva", porque são medidos ao longo de curvas nos (V,T)} superfície.

Teoria clássica para calorimetria de volume constante (isocórica)

A calorimetria de volume constante é a calorimetria realizada a um volume constante. Isso envolve o uso de um calorímetro de volume constante. O calor ainda é medido pelo princípio de calorimetria mencionado acima.

Isso significa que em um calorímetro adequadamente construído, chamado de calorímetro de bomba, o incremento de volume δ δ V{displaystyle delta V } pode ser feito para desaparecer, δ δ V= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle delta V=0 }. Para calorimetria de volume constante:

δ δ Q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =CVδ δ T{displaystyle delta Q=C_{V}delta T.

onde

δ δ T{displaystyle delta T. denota o incremento na temperatura e

CVNão. C_{V} } denota a capacidade de calor em volume constante.

Cálculo de calor clássico em relação à pressão

Da regra acima de cálculo de calor em relação ao volume, segue-se uma em relação à pressão.

Em um processo de pequenos incrementos, δ δ p{displaystyle delta p } de sua pressão, e δ δ T{displaystyle delta T. de sua temperatura, o incremento de calor, δ δ Q{displaystyle delta Q }, ganho pelo corpo do material calórico, é dado por

δ δ Q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =CT(p)(p,T)δ δ p+Cp(T)(p,T)δ δ T{displaystyle delta Q =C_{T}^{(p)}(p,T),delta p,+,C_{p}^{(T)}(p,T),delta T}

onde

CT(p)(p,T){displaystyle C_{T}^{(p)}(p,T) } denota o calor latente com respeito à pressão, do material calorimétrico a temperatura constante, enquanto o volume e a pressão do corpo são autorizados a variar livremente, à pressão pNão. e temperatura TNão. T.;

Cp(T)(p,T){displaystyle C_{p}^{(T)}(p,T) } denota a capacidade de calor, do material calorimétrico a pressão constante, enquanto a temperatura e o volume do corpo são autorizados a variar livremente, à pressão pNão. e temperatura TNão. T.. É costume escrever Cp(T)(p,T){displaystyle C_{p}^{(T)}(p,T) } simplesmente Cp(p,T){displaystyle C_{p}(p,T) }, ou ainda mais brevemente CpNão. C_{p} }.

As novas quantidades aqui estão relacionadas com as anteriores:

CT(p)(p,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =CT(V)(V,T)∂ ∂ p∂ ∂ V|(V,T){displaystyle C_{T}^{(p)}(p,T)={frac {C_{T}^{(V)}(V,T)}{left.{cfrac {partial p}{partial V}}right|_{(V,T)}}}}

Cp(T)(p,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =CV(T)(V,T)- Sim. - Sim. CT(V)(V,T)∂ ∂ p∂ ∂ T|(V,T)∂ ∂ p∂ ∂ V|(V,T){displaystyle C_{p}^{(T)}(p,T)=C_{V}^{(T)}(V,T)-C_{T}^{(V)}(V,T){frac {left.{cfrac {partial p}{partial T}}right|_{(V,T)}}{left.{cfrac {partial p}{partial V}}right|_{(V,T)}}}}

onde

∂ ∂ p∂ ∂ V|(V,T){displaystyle left.{frac {partial p}{partial V}}right|_{(V,T)}} denota o derivado parcial de p(V,T)} com respeito a VNão. V avaliado (V,T)}

e

∂ ∂ p∂ ∂ T|(V,T){displaystyle left.{frac {partial p}{partial T}}right|_{(V,T)}} denota o derivado parcial de p(V,T)} com respeito a TNão. T. avaliado (V,T)}.

Os calores latentes CT(V)(V,T){displaystyle C_{T}^{(V)}(V,T) } e CT(p)(p,T){displaystyle C_{T}^{(p)}(p,T) } são sempre de sinal oposto.

É comum referir-se à razão de calores específicos como

γ γ (V,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Cp(T)(p,T)CV(T)(V,T){displaystyle gamma (V,T)={frac {C_{p}^{(T)}(p,T)}{C_{V}^{(T)}(V,T)}}} muitas vezes apenas escrito como γ γ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =CpCV{displaystyle gamma ={frac {C_{p}}{C_{V}}}}.

Calorimetria por mudança de fase, a equação de estado mostra uma descontinuidade de salto

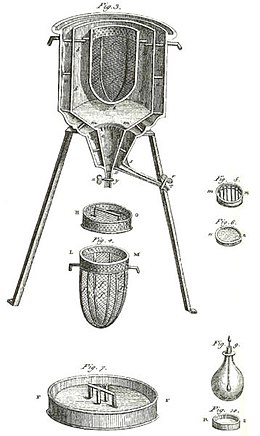
Um calorímetro inicial foi o usado por Laplace e Lavoisier, conforme mostrado na figura acima. Funcionou a temperatura constante e à pressão atmosférica. O calor latente envolvido não era um calor latente em relação ao volume ou em relação à pressão, como no relato acima para calorimetria sem mudança de fase. O calor latente envolvido neste calorímetro era relativo à mudança de fase, ocorrendo naturalmente a temperatura constante. Esse tipo de calorímetro funcionava medindo a massa de água produzida pelo derretimento do gelo, que é uma mudança de fase.

Acumulação de aquecimento

Para um processo dependente do tempo de aquecimento do material calorimétrico, definido por uma progressão conjunta contínua P()1,)2)} de V())} e T()){displaystyle T(t) }, começando a tempo )1Não. t_{1} } e terminando a tempo )2Não. t_{2} }, pode ser calculado uma quantidade acumulada de calor entregue, ? ? Q(P()1,)2)){displaystyle Delta Q(P(t_{1},t_{2}),}. Este cálculo é feito pela integração matemática ao longo da progressão em relação ao tempo. Isso porque os incrementos de calor são 'additivos'; mas isso não significa que o calor é uma quantidade conservadora. A ideia de que o calor era uma quantidade conservadora foi inventada por Lavoisier, e é chamada de "teoria calórica"; no meio do século XIX foi reconhecido como errado. Escrito com o símbolo ? ? {displaystyle Delta }, a quantidade ? ? Q(P()1,)2)){displaystyle Delta Q(P(t_{1},t_{2}),} não é de todo restrito para ser um incremento com valores muito pequenos; isso é em contraste com δ δ Q{displaystyle delta Q }.

Pode-se escrever

? ? Q(P()1,)2)){displaystyle Delta Q(P(t_{1},t_{2}) })

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ P()1,)2)Q:: ())D){displaystyle =int _{P(t_{1},t_{2})}{dot {Q}}(t)dt}

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ P()1,)2)CT(V)(V,T)V:: ())D)+∫ ∫ P()1,)2)CV(T)(V,T)T:: ())D)_{P(t_{1},t_{2})}C_{T}^{(V)}(V,T),{dot {V}}(t),dt,+,int _{P(t_{1},t_{2})}C_{V}^{(T)}(V,T),{dot {T}}(t).

Esta expressão utiliza quantidades como Q:: ())} que são definidos na seção abaixo encabeçada ' Aspectos matemáticos das regras acima'.

Aspectos matemáticos das regras acima

A utilização de quantidades «muito pequenas» tais como δ δ Q{displaystyle delta Q } está relacionado com a exigência física para a quantidade p(V,T)} para ser 'rapidly determinado' por VNão. V e TNão. T.; tal 'determinação rápida' refere-se a um processo físico. Estas quantidades "muito pequenas" são utilizadas na abordagem Leibniz para o cálculo infinitesimal. A abordagem de Newton usa "fluxions" como V:: ())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =DVD)|){displaystyle {dot {V}}(t)=left.{frac {dV}{dt}}right|_{t}}, o que torna mais óbvio que p(V,T)} deve ser 'rapidly determinado'.

Em termos de fluxões, a primeira regra de cálculo acima pode ser escrita

Q:: ())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =CT(V)(V,T)V:: ())+CV(T)(V,T)T:: ()){displaystyle {dot {Q}}(t) =C_{T}^{(V)}(V,T),{dot {V}}(t),+,C_{V}^{(T)}(V,T),{dot {T}}(t)}

onde

)Não. denota o tempo

Q:: ())} denota a taxa de tempo de aquecimento do material calorimétrico no momento )Não.

V:: ()){displaystyle {dot {V}}(t) } denota a taxa de tempo de mudança de volume do material calorimétrico no momento )Não.

T:: ()){displaystyle {dot {T}}(t) } denota a taxa de tempo de mudança da temperatura do material calorimétrico.

O incremento δ δ Q{displaystyle delta Q } e o fluxo Q:: ())} são obtidos por um determinado tempo )Não. que determina os valores das quantidades nos lados direito das regras acima referidas. Mas esta não é uma razão para esperar que exista uma função matemática Q(V,T)}. Por esta razão, o incremento δ δ Q{displaystyle delta Q } é dito ser um "diversitário perfeito" ou um "diferenciamento inexato". Alguns livros indicam isso por escrito q- Sim. em vez de δ δ Q{displaystyle delta Q }. Além disso, a notação đQ é usado em alguns livros. A falta de cuidado com isso pode levar ao erro.

A quantidade ? ? Q(P()1,)2)){displaystyle Delta Q(P(t_{1},t_{2}) }) é adequadamente dito ser um funcional da progressão conjunta contínua P()1,)2)} de V())} e T()){displaystyle T(t) }, mas, na definição matemática de uma função, ? ? Q(P()1,)2)){displaystyle Delta Q(P(t_{1},t_{2}) }) não é uma função de (V,T)}. Embora o fluxion Q:: ())} é definido aqui como uma função do tempo )Não., os símbolos QNão. Q e Q(V,T)} respectivamente em pé sozinho não são definidos aqui.

Âmbito físico das regras de calorimetria acima

As regras acima referem-se apenas a materiais calorimétricos adequados. Os termos 'rapidamente' e 'muito pequeno' exigem a verificação física empírica do domínio de validade das regras acima.

As regras acima para o cálculo do calor pertencem à calorimetria pura. Eles não fazem referência à termodinâmica e eram mais compreendidos antes do advento da termodinâmica. Eles são a base do 'thermo' contribuição para a termodinâmica. A 'dinâmica' contribuição é baseada na ideia de trabalho, que não é utilizada nas regras de cálculo acima.

Coeficientes convenientemente medidos experimentalmente

Empiricamente, é conveniente medir propriedades de materiais calorimétricos sob condições controladas experimentalmente.

Aumento de pressão a volume constante

Para medições em volume controlado experimentalmente, pode-se usar a suposição, afirmada acima, de que a pressão do corpo de material calorimétrico pode ser expressa em função de seu volume e temperatura.

Para medição em volume controlado experimentalmente constante, o coeficiente isocórico de aumento de pressão com temperatura é definido por

α α V(V,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1p(V,T)∂ ∂ p∂ ∂ V|(V,T){displaystyle alpha _{V}(V,T) ={frac {1}{p(V,T)}}{left.{cfrac {partial p}{partial V}}right|_{(V,T)}}}

Expansão a pressão constante

Para medições em pressão experimentalmente controlada, presume-se que o volume VNão. V do corpo do material calorimétrico pode ser expresso como uma função V(T,p)} de sua temperatura TNão. T. e pressão pNão.. Esta suposição está relacionada, mas não é a mesma que, a suposição acima utilizada de que a pressão do corpo de material calórico é conhecida como uma função de seu volume e temperatura; o comportamento anômalo de materiais pode afetar esta relação.

A quantidade que é convenientemente medida a pressão controlada experimentalmente constante, o coeficiente de expansão de volume isóbaro, é definido por

β β p(T,p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1V(T,p)∂ ∂ V∂ ∂ T|(T,p){displaystyle beta _{p}(T,p) ={frac {1}{V(T,p)}}{left.{cfrac {partial V}{partial T}}right|_{(T,p)}}}

Compressibilidade a temperatura constante

Para medições em temperatura experimentalmente controlada, é novamente assumido que o volume VNão. V do corpo do material calorimétrico pode ser expresso como uma função V(T,p)} de sua temperatura TNão. T. e pressão pNão., com o mesmo provisos como mencionado acima.

A quantidade que é convenientemente medida em temperatura constante controlada experimentalmente, a compressibilidade isotérmica, é definida por

κ κ T(T,p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 1V(T,p)∂ ∂ V∂ ∂ p|(T,p){displaystyle kappa _{T}(T,p) =-{frac {1}{V(T,p)}}{left.{cfrac {partial V}{partial p}}right|_{(T,p)}}}

Relação entre grandezas calorimétricas clássicas

Assumindo que a regra p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =p(V,T)} é conhecido, pode-se derivar a função de ∂ ∂ p∂ ∂ T{displaystyle } p) T}} que é usado acima no cálculo de calor clássico com respeito à pressão. Esta função pode ser encontrada experimentalmente a partir dos coeficientes β β p(T,p){displaystyle beta _{p}(T,p) } e κ κ T(T,p){displaystyle kappa _{T}(T,p) } através da relação matematicamente dedutível

∂ ∂ p∂ ∂ T= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =β β p(T,p)κ κ T(T,p){displaystyle } p) T}}={frac {beta _{p}(T,p)}{kappa _{T}(T,p)}}}.

Conexão entre calorimetria e termodinâmica

A termodinâmica desenvolveu-se gradualmente ao longo da primeira metade do século XIX, com base na teoria da calorimetria acima, que havia sido elaborada antes dela, e em outras descobertas. De acordo com Gislason e Craig (2005): "A maioria dos dados termodinâmicos vem da calorimetria..." Segundo Kondepudi (2008): "A calorimetria é amplamente utilizada nos laboratórios atuais."

Em termos de termodinâmica, a energia interna UNão. Não. do material calorimétrico pode ser considerado como o valor de uma função U(V,T)} de (V,T)}, com derivados parciais ∂ ∂ U∂ ∂ V{displaystyle } U'spartial V}} } e ∂ ∂ U∂ ∂ T{displaystyle } U }.

Então pode ser mostrado que é possível escrever uma versão termodinâmica das regras calorimétricas acima:

δ δ Q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.p(V,T)+∂ ∂ U∂ ∂ V|(V,T)]δ δ V+∂ ∂ U∂ ∂ T|(V,T)δ δ T{displaystyle delta Q =left[p(V,T),+left.{frac {partial U}{partial V}}right|_{(V,T)}right],delta V,+,left.{frac {partial U}{partial T}}right|_{(V,T)},delta T.

com

CT(V)(V,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =p(V,T)+∂ ∂ U∂ ∂ V|(V,T)Não. C_{T}^{(V)}(V,T)=p(V,T),+left.{frac {partial U}{partial V}}right|_{(V,T)} }

e

CV(T)(V,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ U∂ ∂ T|(V,T){displaystyle C_{V}^{(T)}(V,T)=left.{frac {partial U}{partial T}}right|_{(V,T)} }.

Mais uma vez, em termos de termodinâmica, a energia interna UNão. Não. do material calorimétrico pode às vezes, dependendo do material calorimétrico, ser considerado como o valor de uma função U(p,T)} de (p,T)(p,T) }, com derivados parciais ∂ ∂ U∂ ∂ p{displaystyle {frac {partial U}{partial p}} } e ∂ ∂ U∂ ∂ T{displaystyle } U }e com VNão. V ser expressível como o valor de uma função V(p,T)} de (p,T)(p,T) }, com derivados parciais ∂ ∂ V∂ ∂ p{displaystyle } V} e ∂ ∂ V∂ ∂ T{displaystyle } V) T}}.

Então, de acordo com Adkins (1975), pode-se mostrar que é possível escrever uma versão termodinâmica adicional das regras calorimétricas acima:

δ δ Q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.∂ ∂ U∂ ∂ p|(p,T)+p∂ ∂ V∂ ∂ p|(p,T)]δ δ p+Não.∂ ∂ U∂ ∂ T|(p,T)+p∂ ∂ V∂ ∂ T|(p,T)]δ δ T{displaystyle delta Q =left[left.{frac {partial U}{partial p}}right|_{(p,T)},+,pleft.{frac {partial V}{partial p}}right|_{(p,T)}right]delta p,+left[left.{frac {partial U}{partial T}}right}

com

CT(p)(p,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ U∂ ∂ p|(p,T)+p∂ ∂ V∂ ∂ p|(p,T){displaystyle C_{T}^{(p)}(p,T)=left.{frac {partial U}{partial p}}right|_{(p,T)},+,pleft.{frac {partial V}{partial p}}right|_{(p,T)} ?

e

Cp(T)(p,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ U∂ ∂ T|(p,T)+p∂ ∂ V∂ ∂ T|(p,T){displaystyle C_{p}^{(T)}(p,T)=left.{frac {partial U}{partial T}}right|_{(p,T)},+,pleft.{frac {partial V}{partial T}}right|_{(p,T)} }.

Além do fato calorimétrico observado acima que o calor latente CT(V)(V,T){displaystyle C_{T}^{(V)}(V,T) } e CT(p)(p,T){displaystyle C_{T}^{(p)}(p,T) } são sempre de sinal oposto, pode ser mostrado, usando o conceito termodinâmico de trabalho, que também

CT(V)(V,T)∂ ∂ p∂ ∂ T|(V,T)≥ ≥ 0.{displaystyle C_{T}^{(V)}(V,T),left.{frac {partial p}{partial T}}right|_{(V,T)}geq 0,}

Especial interesse da termodinâmica em calorimetria: os segmentos isotérmicos de um ciclo de Carnot

A calorimetria tem um benefício especial para a termodinâmica. Ele fala sobre o calor absorvido ou emitido no segmento isotérmico de um ciclo de Carnot.

Um ciclo de Carnot é um tipo especial de processo cíclico que afeta um corpo composto de material adequado para uso em uma máquina térmica. Tal material é do tipo considerado em calorimetria, como observado acima, que exerce uma pressão que é rapidamente determinada apenas pela temperatura e pelo volume. Diz-se que tal corpo muda reversivelmente. Um ciclo de Carnot consiste em quatro estágios ou segmentos sucessivos:

(1) uma mudança de volume de um volume VumNão. V_{a} } a um volume Vb)Não. V_{b} } a temperatura constante T+Não. T^{+} } para incorrer em um fluxo de calor no corpo (conhecido como uma mudança isotérmica)

(2) uma mudança de volume Vb)Não. V_{b} } a um volume VcNão. V_{c} } em uma temperatura variável, como incorrer em nenhum fluxo de calor (conhecido como uma mudança adiabática)

(3) outra alteração isotérmica do volume VcNão. V_{c} } a um volume VDNão. V_{d} } a temperatura constante T- Sim. - Sim. Não. T^{-} } como incorrer em um fluxo ou calor fora do corpo e apenas como preparar precisamente para a seguinte mudança

(4) outra mudança adiabática do volume VDNão. V_{d} } voltar a VumNão. V_{a} } como devolver o corpo à sua temperatura inicial T+Não. T^{+} }.

No segmento isotérmico (1), o calor que flui para o corpo é dado por

? ? Q(Vum,Vb);T+)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ VumVb)CT(V)(V,T+)DVNão. Delta Q(V_{a},V_{b};T^{+}) ,=,,,,,,,,,,,int _{V_{a}}^{V_{b}}C_{T}^{(V)}(V,T^{+}),dV }

e no segmento isotérmico (3) o calor que sai do corpo é dado por

- Sim. - Sim. ? ? Q(Vc,VD;T- Sim. - Sim. )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ∫ ∫ VcVDCT(V)(V,T- Sim. - Sim. )DVNão. - Delta Q(V_{c},V_{d};T^{-}),=,-int _{V_{c}}^{V_{d}}C_{T}^{(V)}(V,T^{-}),dV }.

Como os segmentos (2) e (4) são adiabáticos, nenhum calor flui para dentro ou para fora do corpo durante eles e, consequentemente, o calor líquido fornecido ao corpo durante o ciclo é dado por

? ? Q(Vum,Vb);T+;Vc,VD;T- Sim. - Sim. )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? Q(Vum,Vb);T+)+? ? Q(Vc,VD;T- Sim. - Sim. )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ VumVb)CT(V)(V,T+)DV+∫ ∫ VcVDCT(V)(V,T- Sim. - Sim. )DVNão. Delta Q(V_{a},V_{b};T^{+};V_{c},V_{d};T^{-}),=, Delta Q(V_{a},V_{b};T^{+}),+, Delta Q(V_{c},V_{d};T^{-}),=,int _{V_{a}}^{V_{b}}C_{T}^{(V)}(V,T^{+}),dV,+,int _{V_{c}}^{V_{d}}C_{T}^{(V)}(V,T^{-}),dV }.

Esta quantidade é usada pela termodinâmica e está relacionada de forma especial ao trabalho líquido feito pelo corpo durante o ciclo do Carnot. A mudança líquida da energia interna do corpo durante o ciclo do Carnot, ? ? U(Vum,Vb);T+;Vc,VD;T- Sim. - Sim. )Não. Delta U(V_{a},V_{b};T^{+};V_{c},V_{d};T^{-}) ?, é igual a zero, porque o material do corpo de trabalho tem as propriedades especiais observadas acima.

Especial interesse da calorimetria em termodinâmica: relações entre grandezas calorimétricas clássicas

Relação do calor latente em relação ao volume e a equação de estado

A quantidade CT(V)(V,T){displaystyle C_{T}^{(V)}(V,T) }, o calor latente com respeito ao volume, pertence à calorimetria clássica. Ele responde pela ocorrência de transferência de energia por trabalho em um processo em que o calor também é transferido; a quantidade, no entanto, foi considerada antes da relação entre transferências de calor e trabalho foi clarificada pela invenção da termodinâmica. À luz da termodinâmica, a quantidade calorimétrica clássica é revelada como sendo fortemente ligada à equação de estado do material calorimétrico p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =p(V,T)}. Desde que a temperatura TNão. T, é medida na escala absoluta termodinâmica, a relação é expressa na fórmula

CT(V)(V,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =T∂ ∂ p∂ ∂ T|(V,T){displaystyle C_{T}^{(V)}(V,T)=Tleft.{frac {partial p}{partial T}}right|_{(V,T)} }.

Diferença de calores específicos

A termodinâmica avançada fornece a relação

Cp(p,T)- Sim. - Sim. CV(V,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.p(V,T)+∂ ∂ U∂ ∂ V|(V,T)]∂ ∂ V∂ ∂ T|(p,T){displaystyle C_{p}(p,T)-C_{V}(V,T)=left[p(V,T),+left.{frac {partial U}{partial V}}right|_{(V,T)}right]left.{frac {partial V}{partial T}}right|_{p,T)}}}}.

A partir disso, mais raciocínio matemático e termodinâmico leva a outra relação entre quantidades calorimétricas clássicas. A diferença de calores específicos é dada por

Cp(p,T)- Sim. - Sim. CV(V,T)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =TVβ β p2(T,p)κ κ T(T,p){displaystyle C_{p}(p,T)-C_{V}(V,T)={frac {TV,beta _{p}^{2}(T,p)}{kappa _{T}(T,p)}}}.

Calorimetria prática de volume constante (calorimetria de bomba) para estudos termodinâmicos

A calorimetria de volume constante é a calorimetria realizada a um volume constante. Isso envolve o uso de um calorímetro de volume constante.

Nenhum trabalho é realizado na calorimetria a volume constante, então o calor medido é igual à mudança na energia interna do sistema. A capacidade térmica a volume constante é considerada independente da temperatura.

O calor é medido pelo princípio da calorimetria.

q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =CV? ? T= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? U,Não. q=C_{V}Delta T=Delta U,,

onde

?U é a mudança na energia interna,

?T é mudança na temperatura e

C_V é a capacidade de calor em volume constante.

Na calorimetria de volume constante, a pressão não é mantida constante. Se houver uma diferença de pressão entre os estados inicial e final, o calor medido precisa ser ajustado para fornecer a mudança de entalpia. Um então tem

? ? H. H. H.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? U+? ? (PV)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? U+V? ? P,Não. Delta H=Delta U+Delta (PV)= Delta U+VDelta P,

onde

?H. H. H. é a mudança na enthalpy e

V é o volume imutável da câmara de amostra.

Livros

• Adkins, C.J. (1975). Termodinâmica do Equilíbrio, segunda edição, McGraw-Hill, London, ISBN 0-07-084057-1.
• Bailyn, M. (1994). Pesquisa de Termodinâmica, American Institute of Physics, New York, ISBN 0-88318-797-3.
• Bryan, G.H. (1907). Termodinâmica. Um Tratado Introdutório que lida principalmente com Primeiros Princípios e suas Aplicações DiretasB.G. Tuebner, Leipzig.
• Callen, H.B. (1960/1985). Termodinâmica e uma Introdução à Termostatística, segunda edição, Wiley, New York, ISBN 981-253-185-8.
• Crawford, F.H. (1963). Calor, termodinâmica e física estatística, Rupert Hart-Davis, Londres, Harcourt, Brace, & World.
• Guggenheim, E.A. (1949/1967). Termodinâmica. Um tratamento avançado para químicos e médicosNorth-Holland, Amesterdão.
• Iribarne, J.V., Godson, W.L. (1973/1981), Termodinâmica Atmosférica, segunda edição, D. Reidel, Kluwer Academic Publishers, Dordrecht, ISBN 90-277-1296-4.
• Kondepudi, D. (2008). Introdução à Termodinâmica Moderna, Wiley, Chichester, ISBN 978-0-470-01598-8.
• Landsberg, P.T. (1978). Mecânica Termodinâmica e Estatística, Oxford University Press, Oxford, ISBN 0-19-851142-6.
• Lewis, G.N., Randall, M. (1923/1961). Termodinâmica, segunda edição revisada por K.S Pitzer, L. Brewer, McGraw-Hill, Nova Iorque.
• Maxwell, J.C. (1872). Teoria do calor, terceira edição, Longmans, Green e Co., Londres.
• Partington, J.R. (1949). Um tratado avançado sobre a química física, Volume 1, Princípios Fundamentais. Propriedades de GasesLongmans, Green e Co., Londres.
• Planck, M. (1923/1926). Tratado sobre Termodinâmica, terceira edição em inglês traduzida por A. Ogg da sétima edição alemã, Longmans, Green & Co., Londres.
• Truesdell, C., Bharatha, S. (1977). Conceitos e Lógica da Termodinâmica Clássica como Teoria dos Motores de Calor, rigorosamente construída sobre a Fundação Laid por S. Carnot e F. Reech, Springer, New York, ISBN 0-387-07971-8.