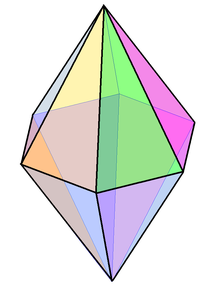
Bipirâmide

AjustarCompartirImprimirCitar

Polyhedron formado unindo pirâmides de espelhamento base-para-base

Conjunto de dual-uniform $n$ - bipirâmides carnais
Exemplo: dual-uniform bipirâmide hexagonal ( $n = 6$ )
Tipo	dual-uniform no sentido de poliedro dual-semiregular
Diagrama de Coxeador
Símbolo de Schläfli	$Não. n ?$
Caras	$2 n$ triângulos isosceles congruentes
Bordas	$3 n$
Versículos	$2 + n$
Configuração da face	$V4.4. n$
Grupo de simetria	$Dnh, n,2, n 22),$ ordem $4 n$
Grupo de rotação	$D n, n,2 +, n 22),$ ordem $2 n$
Poliéster duplo	(convexo) uniforme n-gonal prism
Propriedades	convexo, face-transitivo, vértices regulares
Rede	Exemplo: net of pentagonal bipyramid ( $n = 5$ )

A (simétrica) $n$ -gonal bipirâmide ou dipirâmide é um poliedro formado pela junção de uma pirâmide $n$ -gonal e sua imagem espelhada base a base. Uma bipirâmide $n$ -gonal tem $2 n$ faces triangulares, $3 n$ arestas e $2 + n$ vértices.

O " $n$ -gonal" em nome de uma bipirâmide não se refere a uma face, mas à base do polígono interno, situada no plano do espelho que liga as duas metades da pirâmide. (Se fosse uma face, cada uma de suas arestas conectaria três faces em vez de duas.)

"Regular", bipirâmides direitas

Uma bipirâmide "regular" tem uma base poligonal regular. Geralmente está implícito que também é uma bipirâmide direita.

Uma bipirâmide direita tem seus dois ápices direita acima e direita abaixo do centro ou centróide de sua base poligonal.

Um "normal" direita (simétrica) $n$ -bipirâmide gonal tem o símbolo Schläfli ${ } + {n$ }.

Uma bipirâmide direita (simétrica) tem o símbolo Schläfli ${ } + P$ , para a base do polígono $P$ .

O "regular" direito (portanto face-transitivo) $n$ -bipirâmide gonal com vértices regulares é o dual do $n$ -prisma uniforme (portanto, direito) e tem faces de triângulo isósceles congruentes.

Um "normal" direita (simétrica) $n$ -bipirâmide gonal pode ser projetada em uma esfera ou globo como uma bipirâmide "regular" direita (simétrica) $n$ -gonal bipirâmide esférica: $n$ linhas de longitude igualmente espaçadas indo de pólo a pólo, e uma linha do equador dividindo-as.

Direito "Regular" (simétrico) n- bipirâmides gonais:
Nome de bipyramid	Bipiramida média	Bipiramida triangular (Ver: J12)	Bipiramida quadrada (Ver: O)	Bipiramida Pentagonal (Ver: J13)	Bipiramida hexagonal	Bipiramida heptagonal	Bipiramida octogonal	Bipiramida Enneagonal	Bipiramida Decagonal	...	Bipirâmide Apeirogonal
Imagem de poliedro										...
Imagem de tilagem esférica										Imagem de tilingue plana
Face config.	V2.4.4	V3.4.4	V4.4.4	V5.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Diagrama de Coxeador										...

Bipirâmides de triângulo equilátero

Apenas três tipos de bipirâmides podem ter todas as arestas do mesmo comprimento (o que implica que todas as faces são triângulos equiláteros e, portanto, a bipirâmide é um deltaedro): o "regular" bipirâmides triangulares, tetragonais e pentagonais direitas (simétricas). A bipirâmide tetragonal ou quadrada com arestas do mesmo comprimento, ou octaedro regular, conta entre os sólidos platônicos; as bipirâmides triangulares e pentagonais com arestas de mesmo comprimento contam entre os sólidos de Johnson $(J 12$ e $J 13)$ .

Bipiramidas triangulares equiláteros:
Direito "Regular" (simétrico) nome bipiramida	Bipirâmide trigonal ou triangular $JJ 12$	Bipirâmide tetragonal ou quadrado (Octahedron regular) $O$	Bipiramida Pentagonal $JJ 13$
Imagem bipyramid

Simetria caleidoscópica

Um "regular" direito (simétrico) $n$ -bipirâmide gonal tem grupo de simetria diedral $D n h$ , de ordem $4 n$ , exceto no caso de regular octaedro, que possui o maior grupo de simetria octaédrica $O h$ , de ordem $48$ , que possui três versões de $D 4h$ como subgrupos. O grupo de rotação é $D n$ , de ordem $2 n$ , exceto no caso de um octaedro regular, que possui o maior grupo de rotação $O$ , de ordem $24$ , que tem três versões de $D 4$ como subgrupos.

Observação: todos os "regulares" direita (simétrica) $n$ -bipirâmide gonal tem o mesmo grupo de simetria (diédrica) que a bipirâmide dual-uniforme $n$ -bipirâmide gonal, para $n \neq 4$ .

As $4 n$ faces de um triângulo "regular" direita (simétrica) $2 n$ pirâmide bigonal, projetada como a $4 n$ faces triangulares esféricas de um triângulo "regular" direito (simétrico) $2 n$ -pirâmide esférica bigonal, representam os domínios fundamentais de simetria diedral em três dimensões: $D n h$ , [ $n,2$ ], ( $* n 22$ ), da ordem $4 n$ . Esses domínios podem ser mostrados como triângulos esféricos coloridos alternadamente:

através de um plano de reflexão através de bordas cíclicas, os domínios de imagem de espelho estão em cores diferentes (isometria indireta);
sobre um $n$ -fold ou um $2$ eixo de rotação -fold através de vértices opostos, um domínio e sua imagem estão na mesma cor (isometria direta).

Uma bipirâmide $n$ -gonal (simétrica) pode ser vista como o Kleetope da "correspondente" $n$ diedro-gonal.

Domínios fundamentais da simetria dihedral em três dimensões:
Simetria Dihedral	$D 1h$	$D 2h$	$D 3h$	$D 4h$	$D 5h$	$D 6h$	...	$D n h$
Imagem de domínios fundamentais							...
Diagrama de Coxeador							...

Volume

Volume de uma bipirâmide (simétrica):

{displaystyle V={frac {2}{3}}Bh,}

B

h

Isso funciona para qualquer formato da base e para qualquer localização dos ápices, desde que $h$ seja medido como o distância perpendicular do plano base a qualquer vértice. Por isso:

Volume de uma bipirâmide (simétrica) cuja base é um polígono regular $n$ de lados com comprimento lateral $s$ e cuja altura é $h$ :

{displaystyle V={frac {n}{6}}hs^{2}cot {frac {pi }{n}}.}

Oblique bipyramids

As bipirâmides não direitas são chamadas de bipirâmides oblíquas.

Bipirâmides côncavas

Uma bipirâmide côncava tem uma base poligonal côncava.

Exemplo: concave (symmetric) tetragonal bipyramid (

n = 4

) (*)

(*) Sua base não tem um centro óbvio; mas se seus ápices estão direito acima e direito abaixo do centróide de sua base, então é uma bipirâmide direita. De qualquer forma, é um octaedro côncavo.

Bipirâmides direitas assimétricas/invertidas

Uma bipirâmide reta assimétrica une duas pirâmides direitas com bases congruentes, mas alturas desiguais, base a base.

Uma bipirâmide direita invertida une duas pirâmides direita com bases congruentes, mas alturas desiguais, base a base, mas do mesmo lado de sua base comum.

O dual de uma bipirâmide assimétrica/invertida $n$ -gonal é um estilo n-gonal frustum.

Um "normal" direita assimétrica/invertida $n$ -bipirâmide gonal tem grupo de simetria $C n v$ , de ordem $2 n$ .

Exemplos: Bipiramidas hexagonais direitas assimétricas/invertidas ( $n = 6$ :
Assimétrico	Invertido

Bipirâmides do triângulo escaleno

Exemplo: ditetragonal bipyramid (

2 n = 2\times4

)

Um "isotoxal" direita (simétrica) di- $n$ -gonal bipirâmide é uma bipirâmide direita (simétrica) $2 n$ gonal com uma base isotoxal do polígono plano: seus $2 n$ vértices basais são coplanares, mas alternam-se em dois raios.

Todas as suas faces são triângulos escalenos congruentes e é isoédrica. Ele pode ser visto como outro tipo de "simétrico" escalenoedro di- $n$ -gonal, com base poligonal plana isotoxal.

Um "isotoxal" di- $n$ -gonal bipirâmide direita (simétrica) tem $n$ eixos de rotação dupla através de vértices basais opostos, $n$ planos de reflexão através de bordas apicais opostas, um $eixo de rotação de n$ dobras através dos ápices, um plano de reflexão através da base e um $n$ -dobre o eixo de rotação-reflexão através dos ápices, representando o grupo de simetria $D n h, [n,2], (*22 n),$ da ordem $4 n$ . (A reflexão sobre o plano base corresponde à reflexão de rotação $0°$ . Se $n$ é par, então há uma simetria de inversão sobre o centro, correspondendo à reflexão-rotação $180°$ .)

Exemplo com $2 n = 2\times3$ :

Uma bipirâmida ditrigonal direita (simétrica) tem três planos verticais semelhantes de simetria, intersetando em um (vertical)

3

eixo de rotação -fold; perpendicular a eles é um quarto plano de simetria (horizontal); na interseção dos três planos verticais com o plano horizontal são três semelhantes (horizontal)

2

-fold eixos de rotação; não há centro de simetria de inversão, mas há um centro de simetria: o ponto de interseção dos quatro eixos.

Exemplo com $2 n = 2\times4$ :

Uma bipirâmida ditetragonal direita (simétrica) tem quatro planos verticais de simetria de dois tipos, intersetando em um (vertical)

4

- eixo de rotação dupla; perpendicular a eles é um quinto plano de simetria (horizontal); na interseção dos quatro planos verticais com o plano horizontal são quatro (horizontal)

2

- eixos de rotação dupla de dois tipos, cada perpendicular a um plano de simetria; dois planos verticais bisectam os ângulos entre dois eixos horizontais; e há um centro de simetria de inversão.

Observação: para no máximo dois valores específicos de $z A = | z A' |$ , as faces de tal bipirâmide de triângulo escaleno podem ser isósceles.

Exemplo duplo:

A bipirâmide com isotoxal $2\times2$ - vértices base:

U (1,0,0), U. (-1,0,0), V (0,2,0), V. (0,-2,0)

e com "direita" apices simétricos:

A (0,0,1), A = (0,0,-1),

tem seus rostos isosceles. De facto:

comprimentos de borda apical superior:

{displaystyle {sqrt {2}},}

{displaystyle {sqrt {5}};}

comprimento da borda da base:

{displaystyle {sqrt {5}};}

comprimentos de borda apical inferiores

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

superiores.

A bipirâmida com os mesmos vértices de base, mas com "direita" apices simétricos:

A = (0,0,2), A = (0,0,-2),

também tem seus rostos isosceles. De facto:

comprimentos de borda apical superior:

{displaystyle {sqrt {5}},}

{displaystyle {sqrt {2}};}

comprimento da borda base

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

{displaystyle {sqrt {5}};}

comprimentos de borda apical inferiores

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

superiores.

Na cristalografia, "isotoxal" direita (simétrica) "didigonal" (*) ( $8$ faces), ditrigonal ( $12$ faces), ditetragonal ( $Existem bipirâmides dihexagonais (24 faces) e dihexagonais (24 faces).$

Exemplos de bipiramidas rhombic

(*) As menores bipirâmides $n$ -gonais geométricas têm oito faces e são topologicamente idênticas ao octaedro regular. Neste caso ( $2 n = 2\times2$ ):
um "isotoxal" direita (simétrica) "didigonal" A bipirâmide é chamada de bipirâmide rômbica, embora todas as suas faces sejam triângulos escalenos, porque sua base poligonal plana é um losango.

Escalenoedro

Exemplo: ditrigonal scalenohedron (

2 n = 2 \times 3

)

Um "regular" direito "simétrico" di- $n$ -gonal escalenoedro é definido por uma inclinação regular em zigue-zague $2 n$ -base de gon, dois simétricos ápices à direita acima e à direita abaixo do centro da base e faces triangulares conectando cada borda basal a cada ápice.

Tem dois ápices e $2 n$ vértices basais, $4 n$ faces e $6 n$ arestas; ela é topologicamente idêntica a uma bipirâmide $2 n$ gonal, mas sua $2 n$ vértices basais alternam em dois anéis acima e abaixo do centro.

Todas as suas faces são triângulos escalenos congruentes e é isoédrica. Ele pode ser visto como outro tipo de "simétrico" bipirâmide di- $n$ -gonal, com uma base poligonal regular em zigue-zague.

Um "normal" direito "simétrico" di- $n$ -gonal scalenoedro tem $n$ eixos de rotação dupla através de bordas intermediárias basais opostas, $n$ planos de reflexão através de bordas apicais opostas, um $eixo de rotação de n$ dobras através dos ápices e um $2 n$ -dobre o eixo de rotação-reflexão através dos ápices (sobre os quais $1 n$ rotações- as reflexões preservam globalmente o sólido), representando o grupo de simetria $D n v = D n d, [2 +,2 n], (2* n),$ da ordem $4 n$ . (Se $n$ for ímpar, então existe uma simetria de inversão em torno do centro, correspondente ao $180°$ rotação-reflexão.)

Exemplo com $2 n = 2\times3$ :

A escala ditrigonal "symmetric" direita "regular" tem três planos verticais semelhantes de simetria inclinada um ao outro em

60 °C

e intersecção em um (vertical)

3

- eixo de rotação de dobra, três horizontal semelhante

2

eixos de rotação -fold, cada perpendicular a um plano de simetria, um centro de simetria de inversão, e uma vertical

6

- eixo de rotação-reflexão.

Exemplo com $2 n = 2\times2$ :

A escala "regular" direita "simétrica" "didigonal" escalanohedron tem apenas um vertical e dois horizontal

2

-fold eixos de rotação, dois planos verticais de simetria, que bisectam os ângulos entre o par horizontal de eixos e um vertical

4

-fold eixo de rotação-reflexão; não tem centro de simetria de inversão.

Exemplos de desfenóides e de um

8

- escala facenohedron

Observação: para no máximo dois valores específicos de $z A = | z A' |$ , as faces desse edro escalenopodem ser isósceles.

Exemplo duplo:

O escalanohedron com ziguezague regular skew $2\times2$ - vértices base:

U = (3,0,2), U ' = (-3,0,2), V = (0,3,-2), V ' = (0,-3,-2),

e com "direita" apices simétricos:

A = (0,0,3), A ' = (0,0,-3),

tem seus rostos isosceles. De facto:

comprimentos de borda apical superior:

{displaystyle {sqrt {10}},}

{displaystyle {sqrt {34}};}

comprimento da borda da base:

{displaystyle {sqrt {34}};}

comprimentos de borda apical inferiores

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Mais alto.

O scalenohedron com os mesmos vértices de base, mas com "direita" apices simétricos:

A = (0,0,7), A ' = (0,0,-7),

também tem seus rostos isosceles. De facto:

comprimentos de borda apical superior:

{displaystyle {sqrt {34}},}

{displaystyle {sqrt {10}};}

comprimento da borda base

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

{displaystyle {sqrt {34}};}

comprimentos de borda apical inferiores

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Mais alto.

Em cristalografia, "regular" direito "simétrico" "didigonal" Existem escalenoedros ( $8$ faces) e ditrigonais ( $12$ faces).

Os menores escalenoedros geométricos têm oito faces e são topologicamente idênticos ao octaedro regular. Neste caso ( $2 n = 2\times2$ ), em cristalografia, um "regular" direito "simétrico" "didigonal" ( $8$ faces) escalenoedro é chamado de escalenoedro tetragonal.

Vamos nos concentrar temporariamente no "regular" direito "simétrico" Escalenoedro $8$ faces com $h = r,$ ou seja, $z A = | z A' | = x U = | x U' | = y V = | y V' |$ . Seus dois ápices podem ser representados como $A = (0,0,1), A' = (0,0,- 1),$ e seus quatro vértices basais como $U = (1,0, z), U&# 39; = (-1,0, z), V = (0,1,- z), V' = (0,-1,- z),$ onde $z$ é um parâmetro entre $0$ e $1$ .
Em $z = 0$ , é um octaedro regular; em $z = 1$ , ele tem quatro pares de faces coplanares, e fundi-los em quatro triângulos isósceles congruentes torna-o um bisfenóide; para $z > 1$ , é côncavo.

Exemplo: variações geométricas com "regular" direito "simétrico" $8$ - escala faced nohedra:
$zangão. = 0,1$	$zangão. = 0,25$	$zangão. = 0,5$	$zangão. = 0,95$	$zangão. = 1,5$

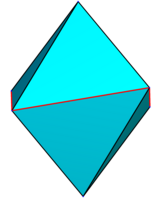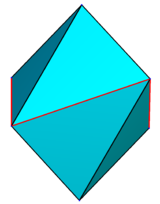Observação: se a base $2 n$ -gon for isotoxal in-out e zigue-zague, então não todas as faces do "isotoxal" direito "simétrico" escalenoedro são congruentes.

Exemplo com cinco comprimentos de borda diferentes:

O scalenohedron com isotoxal em-out zigzag skew

2\times2

- vértices base:

U (1,0,1), U. (-1,0,1), V = (0,2,-1), V. = (0,-2,-1),

e com "direita" apices simétricos:

A = (0,0,3), A = (0,0,-3),

tem rostos superiores congruentes, e faces inferiores congruentes, mas nem todos os seus rostos são congruentes. De facto:

comprimentos de borda apical superior:

{displaystyle {sqrt {5}},}

{displaystyle {sqrt {5}};}

comprimento da borda da base:

UV = VU = U'V = V'U = 3;

comprimentos de borda apical inferiores:

{displaystyle {sqrt {17}},}

{displaystyle {sqrt {2}}.}

Observação: para alguns valores específicos de $z A = | z A' |$ , metade das faces desse edro escalenopode ser isósceles ou equilátero.

Exemplo com três comprimentos de borda diferentes:

O scalenohedron com isotoxal em-out zigzag skew

2\times2

- vértices base:

{displaystyle {sqrt {65}}}

e com "direita" apices simétricos:

A = (0,0,7), A ' = (0,0,-7),

tem faces superiores congruentes, e faces inferiores equiláteros congruentes; assim, nem todos os seus rostos são congruentes. De facto:

comprimentos de borda apical superior:

{displaystyle {sqrt {34}},}

{displaystyle {sqrt {146}};}

comprimento da borda da base:

{displaystyle {sqrt {10}};}

comprimento inferior da borda apical (s):

{displaystyle {sqrt {10}},}

{displaystyle {sqrt {10}}.}

"Normal" bipirâmides estelares

Uma bipirâmide com auto-interseção ou estrela tem uma base polígono estelar.

Um "regular" bipirâmide estelar simétrica direita é definida por uma base poligonal estelar regular, dois ápices simétricos direito acima e direito abaixo do centro da base e, portanto, faces triangulares simétricas um-a-um conectando cada borda basal a cada ápice.

A e#34;regular " A bipirâmide estrela simétrica direita tem faces triangulares isósceles congruentes e é icosaédrica.

Observação: para no máximo um valor específico de $z A = | z A' |$ , os rostos de tal "regular" bipirâmide estrela pode ser equilátero.

A $p / q$ -bipyramid tem diagrama de Coxeter .

Exemplos de bipiramidas estelares simétricas direitas "regulares":
Base de polígono estrela	5/2-gon	7/2.	7/3-gon	8/3-gon	9/2.	9/4-gon
Imagem bipyramid da estrela
Diagrama de Coxeador

Exemplos de bipiramidas estelares simétricas direitas "regulares":
Base de polígono estrela	10/3-gon	11/2.	11/3-gon	11/4-gon	11/5	12/5
Imagem bipyramid da estrela
Diagrama de Coxeador

Triângulo escaleno bipirâmide estrela

Um "isotoxal" direita simétrica $2 p / q$ -gonal estrela bipirâmide é definida por uma estrela $2 p / q$ -gon base, dois ápices simétricos à direita acima e à direita abaixo do centro da base, e assim faces triangulares simétricas um-para-um conectando cada borda basal a cada ápice.

Um "isotoxal" A bipirâmide estrela $2 p / q$ simétrica direita tem faces triangulares escalenas congruentes e é isoédrica. Ele pode ser visto como outro tipo de $2 p / q$ -gonal direita "simétrica" escalenoedro estrela, com uma base de polígono estrela isotoxal in-out.

Observação: para no máximo dois valores específicos de $z A = | z A' |$ , as faces de tal bipirâmide de estrela triangular escalena podem ser isósceles.

Exemplo de um simétrico direito "isotoxal" 2p/q- bipirâmide estrelagonal:
Base de polígono estrela	Isotoxal in-out 8/3-gon
Escalane triângulo estrela bipyramid imagem

Estrela escalenoedra

Um "regular" direito "simétrico" $2 p / q$ -gonal estrela escalenoedro é definido por uma inclinação regular em zigue-zague estrela $2 p / q$ -gon base, dois ápices simétricos direita acima e direita abaixo do centro da base e faces triangulares conectando cada borda basal a cada ápice.

Um "normal" direito "simétrico" $2 p / q$ estrela escalenoedro tem faces triangulares escalenas congruentes e é isoédrica. Ele pode ser visto como outro tipo de "simétrico" $2 p / q$ bipirâmide em estrela gonal, com uma base polígono em estrela regular em zigue-zague.

Observação: para no máximo dois valores específicos de $z A = | z A' |$ , as faces de tal estrela scalenoedro podem ser isósceles.

Exemplo de um "regular" direito "simétrico" 2p/q-gonal estrela escalanohedron:
Base de polígono estrela	ziguezague regular skew 8/3-gon
Imagem em escala estelar

Observação: se a base $2 p / q$ -gon estrela for isotoxal de entrada e saída e inclinação em zigue-zague, então não todas as faces do "isotoxal" direito "simétrico" escalenoedro estrela são congruentes.

Exemplo de um "isotoxal" direito "simétrico" 2p/q-gonal estrela escalanohedron:
Base de polígono estrela	Isotoxal em ziguezague skew 8/3-gon
Imagem em escala estelar

Observação: para alguns valores específicos de $z A = | z A' |$ , metade das faces de tal estrela scalenoedro pode ser isósceles ou equilátero.

Exemplo com quatro comprimentos de borda diferentes:

A estrela scalenohedron com isotoxal in-out zigzag skew

8/3

- vértices base:

U 0 (1,0,1), U 1 = (0,1,1), U 2 (-1,0,1), U 3 = (0,-1,1),

V 0 = (2,2,-1), V 1 = (-2,2,-1), V 2 = (-2,-2,-1), V 3 = (2,-2,-1),

e com "direita" apices simétricos:

A = (0,0,3), A = (0,0,-3),

tem faces superiores congruentes e isosceles congruentes face inferior; assim, nem todos os seus rostos são congruentes. De facto:

comprimentos de borda apical superior:

{displaystyle {sqrt {5}},}

{displaystyle {sqrt {6}};}

comprimento da borda da base:

{displaystyle {sqrt {17}};}

comprimentos de borda apical inferiores:

{displaystyle {sqrt {17}},}

{displaystyle {sqrt {3}}.}

Exemplo com três comprimentos de borda diferentes:

A estrela scalenohedron com isotoxal in-out zigzag skew

8/3

- vértices base:

{sqrt {2}}

{sqrt {2}}

e com "direita" apices simétricos:

{sqrt {2}}

tem faces superiores congruentes, e faces inferiores equiláteros congruentes; assim, nem todos os seus rostos são congruentes. De facto:

comprimentos de borda apical superior:

{displaystyle {sqrt {22}},}

{displaystyle {sqrt {2}};}

comprimento da borda da base:

comprimento inferior da borda apical (s):

A'U 0 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = A'U 1 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = A'U 2 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = A'U 3 - 12,

A'V 0 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = A'V 1 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = A'V 2 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = A'V 3 = 12.

4-politopos com células bipiramidais

O dual da retificação de cada 4-politopos regulares convexos é um 4-politopo celular transitivo com células bipiramidais. A seguir, o vértice do vértice da bipirâmide é A e um vértice do equador é E. A distância entre os vértices adjacentes no equador EE = 1, o vértice até a borda do equador é AE e a distância entre os vértices é AA. A bipirâmide 4-politopo terá vértices V_A onde os ápices das bipirâmides N_A se encontram. Terá vértices V_E onde se encontram os vértices do tipo E das bipirâmides N_E. N_AE bipirâmides se encontram ao longo de cada aresta do tipo AE. N_EE bipirâmides se encontram ao longo de cada aresta do tipo EE. C_AE é o cosseno do ângulo diedro ao longo de uma aresta AE. C_EE é o cosseno do ângulo diedro ao longo de uma aresta EE. Como as células devem caber em torno de uma borda, N_EE cos⁻¹(C_EE) ≤ 2 $π$ , N_AE cos⁻¹(C_AE) ≤ 2 $π$ .

4-polytopes com células bipyramidal
Propriedades de 4-politope									Propriedades de Bipyramid
Dual de	Medidores de água	Células	V_A	V_E	N_A	N_E	N_AE	N_E	Célula	Coxeador diagrama	AA	AE	C_AE	C_E
Rectificado 5-célula		10.	5	5	4	6	3	3	Bipiramida triangular		${textstyle {frac {2}{3}}}$	0.667	${textstyle -{frac {1}{7}}}$	${textstyle -{frac {1}{7}}}$
Tesser		32	16.	8	4	12	3	4	Bipiramida triangular		${textstyle {frac {sqrt {2}}{3}}}$	0.624	${textstyle -{frac {2}{5}}}$	${textstyle -{frac {1}{5}}}$
Rectificado 24-célula		96	24.	24.	8	12	4	3	Bipiramida triangular		${textstyle {frac {2{sqrt {2}}}{3}}}$	0,7545	${textstyle {frac {1}{11}}}$	${textstyle -{frac {5}{11}}}$
Rectificada 120 células		1200	600	120	4	30	3	5	Bipiramida triangular		${textstyle {frac {{sqrt {5}}-1}{3}}}$	0,613	${textstyle -{frac {10+9{sqrt {5}}}{61}}}$	${textstyle -{frac {7-12{sqrt {5}}}{61}}}$
Rectificado 16 células		24?	8	16.	6	6	3	3	Bipiramida quadrada		${textstyle sqrt{2}}$	1	${textstyle -{frac {1}{3}}}$	${textstyle -{frac {1}{3}}}$
Bebê de mel cúbico retificado		∞	∞	∞	6	12	3	4	Bipiramida quadrada		${textstyle 1}$	0,66	${textstyle -{frac {1}{2}}}$	${textstyle 0}$
Rectificada 600 células		720	120	600	12	6	3	3	Bipiramida Pentagonal		${textstyle {frac {5+3{sqrt {5}}}{5}}}$	1.400	${textstyle -{frac {11+4{sqrt {5}}}{41}}}$	${textstyle -{frac {11+4{sqrt {5}}}{41}}}$

* O rectificado 16-célula é o regular 24-célula e vértices são todos equivalentes – octahedra são bipiramidas regulares.

Não. Dado numericamente devido à forma mais complexa.

Outras dimensões

Em geral, uma bipirâmide pode ser vista como um n-polítopo construído com um (n − 1)-polítopo em um hiperplano com dois pontos em direções opostas e distâncias perpendiculares iguais do hiperplano. Se o politopo (n − 1) for um politopo regular, ele terá facetas piramidais idênticas.

Uma pirâmide bidimensional (e#34;regular ") simétrica direita (diagonal) é formada unindo-se dois triângulos isósceles congruentes base a base; seu contorno é um losango, {}+{}.

Bipirâmides poliédricas

Uma bipirâmide poliédrica é um 4-politopo com uma base poliédrica e um ponto de vértice.

Um exemplo é o de 16 células, que é uma bipirâmide octaédrica, {}+{3,4}, e mais geralmente um n-ortoplexo é um (n − 1)-ortoplex bipirâmide, {}+{3^n-2,4}.

Outras bipirâmides incluem a bipirâmide tetraédrica, {}+{3,3}, a bipirâmide icosaédrica, {}+{3,5} e a bipirâmide dodecaédrica, {}+{5,3}, as duas primeiras tendo todas regular células, eles também são politopos cegos.

Contenido relacionado

Más resultados...

Bipirâmide

"Regular", bipirâmides direitas

Bipirâmides de triângulo equilátero

Simetria caleidoscópica

Volume

Oblique bipyramids

Bipirâmides côncavas

Bipirâmides direitas assimétricas/invertidas

Bipirâmides do triângulo escaleno

Escalenoedro

"Normal" bipirâmides estelares

Triângulo escaleno bipirâmide estrela

Estrela escalenoedra

4-politopos com células bipiramidais

Outras dimensões

Bipirâmides poliédricas

Contenido relacionado

Número computável

Relação de equivalência

Johnson sólido