Bioestatística
Bioestatística (também conhecida como biometria) é o desenvolvimento e aplicação de métodos estatísticos para uma ampla gama de tópicos em biologia. Abrange o projeto de experimentos biológicos, a coleta e análise de dados desses experimentos e a interpretação dos resultados.
História
Bioestatística e genética
A modelagem bioestatística é uma parte importante de várias teorias biológicas modernas. Os estudos de genética, desde o seu início, utilizaram conceitos estatísticos para entender os resultados experimentais observados. Alguns geneticistas chegaram a contribuir com avanços estatísticos com o desenvolvimento de métodos e ferramentas. Gregor Mendel iniciou os estudos genéticos investigando padrões de segregação genética em famílias de ervilhas e usou estatísticas para explicar os dados coletados. No início dos anos 1900, após a redescoberta do trabalho de herança mendeliana de Mendel, havia lacunas na compreensão entre a genética e o darwinismo evolutivo. Francis Galton tentou expandir as descobertas de Mendel com dados humanos e propôs um modelo diferente com frações da hereditariedade vindas de cada ancestral compondo uma série infinita. Ele chamou isso de teoria da "Lei da Hereditariedade Ancestral". Suas ideias foram fortemente discordadas por William Bateson, que seguiu as conclusões de Mendel, de que a herança genética era exclusivamente dos pais, metade de cada um deles. Isso levou a um vigoroso debate entre os biometristas, que apoiavam as ideias de Galton, como Raphael Weldon, Arthur Dukinfield Darbishire e Karl Pearson, e os mendelianos, que apoiavam as ideias de Bateson (e de Mendel), como Charles Davenport e Wilhelm Johannsen. Mais tarde, os biometristas não conseguiram reproduzir as conclusões de Galton em diferentes experimentos, e as ideias de Mendel prevaleceram. Na década de 1930, modelos baseados em raciocínio estatístico ajudaram a resolver essas diferenças e a produzir a síntese evolutiva moderna neodarwinista.
Resolver essas diferenças também permitiu definir o conceito de genética de populações e uniu genética e evolução. As três principais figuras no estabelecimento da genética de populações e esta síntese se basearam na estatística e desenvolveram seu uso na biologia.
- Ronald Fisher trabalhou ao lado da estatística Betty Allan desenvolvendo vários métodos estatísticos básicos em apoio ao seu trabalho estudando os experimentos de cultura na Rothamsted Research, publicado nos livros de Fisher Metodologias Estatísticas para Trabalhadores da Pesquisa (1925) e The Genetical Theory of Natural Selection (1930), bem como nos trabalhos científicos de Allan. Fisher passou a dar muitas contribuições para a genética e estatísticas. Alguns deles incluem o ANOVA, conceitos de p-valor, o teste exato de Fisher e a equação de Fisher para dinâmica populacional. Ele é creditado pela sentença "A seleção natural é um mecanismo para gerar um grau excessivamente elevado de improbabilidade".
- Sewall G. Wright desenvolveu F-estatística e métodos de computá-los e definido coeficiente de incriação.
- O livro de J. B. S. Haldane, As Causas da Evolução, restabelecia a seleção natural como o principal mecanismo da evolução, explicando-a em termos das consequências matemáticas da genética mendeliana. Ele também desenvolveu a teoria da sopa primordial.
Esses e outros bioestatísticos, biólogos matemáticos e geneticistas inclinados à estatística ajudaram a reunir a biologia evolutiva e a genética em um todo consistente e coerente que poderia começar a ser modelado quantitativamente.
Paralelamente a esse desenvolvimento geral, o trabalho pioneiro de D'Arcy Thompson em On Growth and Form também ajudou a adicionar disciplina quantitativa ao estudo biológico.
Apesar da importância fundamental e da frequente necessidade do raciocínio estatístico, pode ter havido uma tendência entre os biólogos de desconfiar ou depreciar os resultados que não são qualitativamente aparentes. Uma anedota descreve Thomas Hunt Morgan banindo a calculadora Friden de seu departamento na Caltech, dizendo "Bem, eu sou como um cara que está procurando ouro nas margens do rio Sacramento em 1849. Com um pouco de inteligência, posso abaixe-se e pegue grandes pepitas de ouro. E enquanto eu puder fazer isso, não vou permitir que nenhuma pessoa do meu departamento desperdice recursos escassos na mineração de placer."
Planejamento de pesquisa
Qualquer pesquisa em ciências da vida é proposta para responder a uma pergunta científica que possamos ter. Para responder a essa pergunta com alta certeza, precisamos de resultados precisos. A definição correta da hipótese principal e do plano de pesquisa reduzirá os erros na tomada de decisão na compreensão de um fenômeno. O plano de pesquisa pode incluir a questão de pesquisa, a hipótese a ser testada, o desenho experimental, métodos de coleta de dados, perspectivas de análise de dados e custos envolvidos. É fundamental realizar o estudo com base nos três princípios básicos da estatística experimental: randomização, replicação e controle local.
Pergunta de pesquisa
A questão de pesquisa definirá o objetivo de um estudo. A pesquisa será encabeçada pela pergunta, por isso precisa ser concisa, ao mesmo tempo em que se concentra em tópicos interessantes e novos que possam aprimorar a ciência e o conhecimento e esse campo. Para definir a forma de fazer a pergunta científica, pode ser necessária uma revisão exaustiva da literatura. Assim, a pesquisa pode ser útil para agregar valor à comunidade científica.
Definição da hipótese
Uma vez definido o objetivo do estudo, podem ser propostas as possíveis respostas à questão de investigação, transformando esta questão numa hipótese. A proposta principal é chamada de hipótese nula (H0) e geralmente é baseada em um conhecimento permanente sobre o tema ou uma ocorrência óbvia dos fenômenos, sustentada por uma profunda revisão da literatura. Podemos dizer que é a resposta padrão esperada para os dados na situação em teste. Em geral, HO não assume associação entre tratamentos. Por outro lado, a hipótese alternativa é a negação de HO. Assume algum grau de associação entre o tratamento e o resultado. No entanto, a hipótese é sustentada pela pesquisa de perguntas e suas respostas esperadas e inesperadas.
Como exemplo, considere grupos de animais semelhantes (camundongos, por exemplo) sob dois sistemas de dieta diferentes. A pergunta de pesquisa seria: qual é a melhor dieta? Nesse caso, H0 seria que não há diferença entre as duas dietas no metabolismo dos camundongos (H0: μ1 = μ2) e a hipótese alternativa seria que as dietas têm diferentes efeitos sobre o metabolismo dos animais (H1: μ1 ≠ μ2).
A hipótese é definida pelo investigador, de acordo com o seu interesse em responder à questão principal. Além disso, a hipótese alternativa pode ser mais de uma hipótese. Ele pode assumir não apenas diferenças entre os parâmetros observados, mas também seu grau de diferença (<i.e. maior ou menor).
Amostragem
Normalmente, um estudo visa entender o efeito de um fenômeno sobre uma população. Em biologia, uma população é definida como todos os indivíduos de uma determinada espécie, em uma área específica em um determinado momento. Em bioestatística, este conceito é estendido a uma variedade de coleções possíveis de estudo. Embora, em bioestatística, uma população não seja apenas os indivíduos, mas o total de um componente específico de seus organismos, como o genoma inteiro, ou todas as células espermáticas, para animais, ou a área foliar total, para uma planta, por exemplo.
Não é possível tirar as medidas de todos os elementos de uma população. Por isso, o processo de amostragem é muito importante para a inferência estatística. A amostragem é definida como obter aleatoriamente uma parte representativa de toda a população, para fazer inferências posteriores sobre a população. Portanto, a amostra pode capturar a maior variabilidade em uma população. O tamanho da amostra é determinado por várias coisas, desde o escopo da pesquisa até os recursos disponíveis. Na pesquisa clínica, o tipo de ensaio, como inferioridade, equivalência e superioridade, é uma chave para determinar o tamanho da amostra.
Design experimental
Os projetos experimentais sustentam os princípios básicos da estatística experimental. Existem três projetos experimentais básicos para alocar tratamentos aleatoriamente em todas as parcelas do experimento. Eles são delineamentos completamente aleatórios, delineamentos de blocos randomizados e delineamentos fatoriais. Os tratamentos podem ser organizados de várias maneiras dentro do experimento. Na agricultura, o desenho experimental correto é a raiz de um bom estudo e a disposição dos tratamentos dentro do estudo é essencial porque o ambiente afeta muito as parcelas (plantas, gado, microorganismos). Esses arranjos principais podem ser encontrados na literatura sob os nomes de "reticulados", "blocos incompletos", "split plot", "blocos aumentados", e muitos outros. Todos os projetos podem incluir parcelas de controle, determinadas pelo pesquisador, para fornecer uma estimativa de erro durante a inferência.
Em estudos clínicos, as amostras são geralmente menores do que em outros estudos biológicos e, na maioria dos casos, o efeito do ambiente pode ser controlado ou medido. É comum usar ensaios clínicos randomizados controlados, onde os resultados são geralmente comparados com desenhos de estudos observacionais, como caso-controle ou coorte.
Coleta de dados
Os métodos de coleta de dados devem ser considerados no planejamento da pesquisa, pois influenciam muito o tamanho da amostra e o desenho experimental.
A coleta de dados varia de acordo com o tipo de dados. Para dados qualitativos, a coleta pode ser feita com questionários estruturados ou por observação, considerando a presença ou intensidade da doença, utilizando o critério de pontuação para categorizar os níveis de ocorrência. Para dados quantitativos, a coleta é feita medindo informações numéricas usando instrumentos.
Em estudos de agricultura e biologia, os dados de produção e seus componentes podem ser obtidos por medidas métricas. No entanto, as injúrias de pragas e doenças nas plantas são obtidas por observação, considerando escalas de pontuação para os níveis de dano. Especialmente, em estudos genéticos, métodos modernos de coleta de dados em campo e laboratório devem ser considerados, como plataformas de alto rendimento para fenotipagem e genotipagem. Essas ferramentas permitem experimentos maiores, ao mesmo tempo em que possibilitam avaliar muitas parcelas em tempo menor do que um método apenas humano para coleta de dados. Por fim, todos os dados de interesse coletados devem ser armazenados em um quadro de dados organizado para posterior análise.
Análise e interpretação de dados
Ferramentas descritivas
Os dados podem ser representados por meio de tabelas ou representações gráficas, como gráficos de linhas, gráficos de barras, histogramas, gráfico de dispersão. Além disso, medidas de tendência central e variabilidade podem ser muito úteis para descrever uma visão geral dos dados. Acompanhe alguns exemplos:
Tabelas de frequência
Um tipo de tabela é a tabela de frequência, que consiste em dados dispostos em linhas e colunas, onde a frequência é o número de ocorrências ou repetições dos dados. A frequência pode ser:
Absoluto: representa o número de vezes que um determinado valor aparece;
Relativo: obtido pela divisão da frequência absoluta pelo número total;
No próximo exemplo, temos o número de genes em dez operons do mesmo organismo.
- Genes = {2,3,3,4,5,3,3,3,3,4}
| Número de genes | Frequência absoluta | Frequência relativa |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 0.1 |
| 3 | 6 | 0.6 |
| 4 | 2 | 0,2 |
| 5 | 1 | 0.1 |
Gráfico de linha

Gráficos de linha representam a variação de um valor sobre outra métrica, como o tempo. Em geral, os valores são representados no eixo vertical, enquanto a variação temporal é representada no eixo horizontal.
Gráfico de barras
Um gráfico de barras é um gráfico que mostra dados categóricos como barras apresentando alturas (barra vertical) ou larguras (barra horizontal) proporcionais para representar valores. Os gráficos de barras fornecem uma imagem que também pode ser representada em um formato tabular.
No exemplo do gráfico de barras, temos a taxa de natalidade no Brasil para os meses de dezembro de 2010 a 2016. A queda acentuada em dezembro de 2016 reflete o surto do vírus Zika na taxa de natalidade no Brasil.
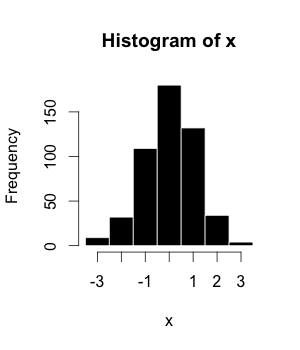
Histogramas
O histograma (ou distribuição de frequência) é uma representação gráfica de um conjunto de dados tabulado e dividido em classes uniformes ou não uniformes. Foi introduzido pela primeira vez por Karl Pearson.
Gráfico de dispersão
Um gráfico de dispersão é um diagrama matemático que usa coordenadas cartesianas para exibir valores de um conjunto de dados. Um gráfico de dispersão mostra os dados como um conjunto de pontos, cada um apresentando o valor de uma variável que determina a posição no eixo horizontal e outra variável no eixo vertical. Eles também são chamados de gráfico de dispersão, gráfico de dispersão, grama de dispersão ou diagrama de dispersão.
Médio
A média aritmética é a soma de uma coleção de valores (x1+x2+x3+⋯ ⋯ +xnNão. {x_{1}+x_{2}+x_{3}+cdots +x_{n}}}) dividido pelo número de itens desta coleção (n(n)).
- x? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nxEu...)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x1+x2+⋯ ⋯ +xnn{displaystyle {bar {x}}={frac {1}{n}}left(sum _{i=1}^{n}{x_{i}}right)={frac {x_{1}+x_{2}+cdots +x_{n}}{n}}}
Média
A mediana é o valor no meio de um conjunto de dados.
Modo
A moda é o valor de um conjunto de dados que aparece com mais frequência.
| Tipo | Exemplo | Resultado |
|---|---|---|
| Meio | (2 + 3 + 3 + 3 + 3 + 3 + 4 + 4 + 11) / 9 | 4 |
| Median | 2, 3, 3, 3, 33, 4, 4, 11 | 3 |
| Modo | 2, 3, 3, 3, 3, 34, 4, 11 | 3 |
Box plot
Box plot é um método para representar graficamente grupos de dados numéricos. Os valores máximos e mínimos são representados pelas linhas, e o intervalo interquartílico (IQR) representa 25-75% dos dados. Outliers podem ser plotados como círculos.
Coeficientes de correlação
Embora as correlações entre dois tipos diferentes de dados possam ser inferidas por gráficos, como o gráfico de dispersão, é necessário validar isso por meio de informações numéricas. Por esta razão, os coeficientes de correlação são necessários. Eles fornecem um valor numérico que reflete a força de uma associação.
Coeficiente de correlação de Pearson
O coeficiente de correlação de Pearson é uma medida de associação entre duas variáveis, X e Y. Esse coeficiente, geralmente representado por ρ (rho) para a população e r para a amostra, assume valores entre −1 e 1, onde ρ = 1 representa uma correlação positiva perfeita, ρ = −1 representa uma correlação negativa perfeita e ρ = 0 não há correlação linear.
Estatísticas inferenciais
É usado para fazer inferências sobre uma população desconhecida, por estimativa e/ou teste de hipótese. Em outras palavras, é desejável obter parâmetros para descrever a população de interesse, mas como os dados são limitados, é necessário fazer uso de uma amostra representativa para estimá-los. Com isso, é possível testar hipóteses previamente definidas e aplicar as conclusões a toda a população. O erro padrão da média é uma medida de variabilidade que é crucial para fazer inferências.
- Teste de hipotese
O teste de hipóteses é essencial para fazer inferências sobre populações com o objetivo de responder a questões de pesquisa, conforme estabelecido em "Planejamento de pesquisa" seção. Os autores definiram quatro etapas a serem definidas:
- A hipótese a ser testada: como afirmado anteriormente, temos que trabalhar com a definição de uma hipótese nula (H)0), isso vai ser testado, e uma hipótese alternativa. Mas eles devem ser definidos antes da implementação do experimento.
- Regra de nível de significância e decisão: Uma regra de decisão depende do nível de significância, ou em outras palavras, da taxa de erro aceitável (α). É mais fácil pensar que definimos um valor crítico que determina a significância estatística quando uma estatística de teste é comparada com ela. Assim, α também tem que ser predefinida antes da experiência.
- Análise experimental e estatística: Isto é quando o experimento é realmente implementado após o projeto experimental apropriado, os dados são coletados e os testes estatísticos mais adequados são avaliados.
- Inferência: É feita quando a hipótese nula é rejeitada ou não rejeitada, com base na evidência de que a comparação de p-valores e α traz. É apontado que o fracasso de rejeitar H0 apenas significa que não há evidências suficientes para apoiar sua rejeição, mas não que essa hipótese seja verdadeira.
- Intervalos de confiança
Um intervalo de confiança é um intervalo de valores que pode conter o verdadeiro valor real do parâmetro em determinado nível de confiança. O primeiro passo é estimar a melhor estimativa não viesada do parâmetro populacional. O valor superior do intervalo é obtido pela soma dessa estimativa com a multiplicação entre o erro padrão da média e o nível de confiança. O cálculo do menor valor é semelhante, mas ao invés de uma soma, deve-se aplicar uma subtração.
Considerações estatísticas
Erro de potência e estatística
Ao testar uma hipótese, existem dois tipos de erros estatísticos possíveis: erro tipo I e erro tipo II. O erro tipo I ou falso positivo é a rejeição incorreta de uma hipótese nula verdadeira e o erro tipo II ou falso negativo é a falha em rejeitar uma hipótese nula falsa. O nível de significância denotado por α é a taxa de erro tipo I e deve ser escolhido antes de realizar o teste. A taxa de erro tipo II é denotada por β e o poder estatístico do teste é 1 − β.
P-valor
O p-valor é a probabilidade de obter resultados tão extremos ou mais extremos do que os observados, assumindo que a hipótese nula (H0) é verdadeira. Também é chamada de probabilidade calculada. É comum confundir o valor de p com o nível de significância (α), mas, o α é um limite predefinido para chamar resultados significativos. Se p for menor que α, a hipótese nula (H0) é rejeitada.
Vários testes
Em testes múltiplos da mesma hipótese, a probabilidade de ocorrência de falsos positivos (taxa de erro familiar) aumenta e algumas estratégias são usadas para controlar essa ocorrência. Isso geralmente é alcançado usando um limite mais rigoroso para rejeitar hipóteses nulas. A correção de Bonferroni define um nível de significância global aceitável, denotado por α* e cada teste é comparado individualmente com um valor de α = α*/m. Isso garante que a taxa de erro familiar em todos os testes m seja menor ou igual a α*. Quando m é grande, a correção de Bonferroni pode ser excessivamente conservadora. Uma alternativa à correção de Bonferroni é controlar a taxa de descoberta falsa (FDR). O FDR controla a proporção esperada de hipóteses nulas rejeitadas (as chamadas descobertas) que são falsas (rejeições incorretas). Este procedimento garante que, para testes independentes, a taxa de falsa descoberta seja no máximo q*. Assim, o FDR é menos conservador do que a correção de Bonferroni e tem mais poder, ao custo de mais falsos positivos.
Especificações incorretas e verificações de robustez
A hipótese principal que está sendo testada (por exemplo, nenhuma associação entre tratamentos e resultados) é frequentemente acompanhada por outras suposições técnicas (por exemplo, sobre a forma da distribuição de probabilidade dos resultados) que também fazem parte da hipótese nula. Quando as suposições técnicas são violadas na prática, o nulo pode ser frequentemente rejeitado mesmo que a hipótese principal seja verdadeira. Tais rejeições são ditas devido à especificação incorreta do modelo. Verificar se o resultado de um teste estatístico não muda quando as suposições técnicas são ligeiramente alteradas (as chamadas verificações de robustez) é a principal forma de combater erros de especificação.
Critérios de seleção de modelo
A seleção de critérios de modelo selecionará ou modelará aquele modelo verdadeiro mais aproximado. O Critério de Informação de Akaike (AIC) e o Critério de Informação Bayesiano (BIC) são exemplos de critérios assintoticamente eficientes.
Desenvolvimentos e big data
Desenvolvimentos recentes tiveram um grande impacto na bioestatística. Duas mudanças importantes foram a capacidade de coletar dados em uma escala de alto rendimento e a capacidade de realizar análises muito mais complexas usando técnicas computacionais. Isso vem do desenvolvimento em áreas como tecnologias de sequenciamento, Bioinformática e Machine Learning (Aprendizado de máquina em bioinformática).
Uso em dados de alto rendimento
Novas tecnologias biomédicas como microarrays, sequenciadores de última geração (para genômica) e espectrometria de massa (para proteômica) geram enormes quantidades de dados, permitindo que muitos testes sejam realizados simultaneamente. Análise cuidadosa com métodos bioestatísticos é necessária para separar o sinal do ruído. Por exemplo, um microarray poderia ser usado para medir muitos milhares de genes simultaneamente, determinando quais deles têm expressão diferente em células doentes em comparação com células normais. No entanto, apenas uma fração dos genes será expressa diferencialmente.
A multicolinearidade geralmente ocorre em configurações bioestatísticas de alto rendimento. Devido à alta intercorrelação entre os preditores (como níveis de expressão gênica), a informação de um preditor pode estar contida em outro. Pode ser que apenas 5% dos preditores sejam responsáveis por 90% da variabilidade da resposta. Nesse caso, pode-se aplicar a técnica bioestatística de redução de dimensão (por exemplo, através da análise de componentes principais). Técnicas estatísticas clássicas como regressão linear ou logística e análise discriminante linear não funcionam bem para dados de alta dimensão (ou seja, quando o número de observações n é menor que o número de características ou preditores p: n < p). Na verdade, pode-se obter valores de R2 bastante altos, apesar do poder preditivo muito baixo do modelo estatístico. Essas técnicas estatísticas clássicas (esp. regressão linear de mínimos quadrados) foram desenvolvidas para dados de baixa dimensão (ou seja, onde o número de observações n é muito maior que o número de preditores p: n >> p). Em casos de alta dimensionalidade, deve-se sempre considerar um conjunto de teste de validação independente e a correspondente soma de quadrados residual (RSS) e R2 do conjunto de teste de validação, não os do conjunto de treinamento.
Muitas vezes, é útil agrupar informações de vários preditores. Por exemplo, a Análise de Enriquecimento de Conjuntos de Genes (GSEA) considera a perturbação de conjuntos de genes inteiros (relacionados funcionalmente) em vez de genes individuais. Esses conjuntos de genes podem ser vias bioquímicas conhecidas ou genes funcionalmente relacionados. A vantagem dessa abordagem é que ela é mais robusta: é mais provável que um único gene seja falsamente perturbado do que todo um caminho seja falsamente perturbado. Além disso, pode-se integrar o conhecimento acumulado sobre vias bioquímicas (como a via de sinalização JAK-STAT) usando essa abordagem.
Avanços da bioinformática em bancos de dados, mineração de dados e interpretação biológica
O desenvolvimento de bases de dados biológicos permite o armazenamento e gestão de dados biológicos com possibilidade de acesso garantido a utilizadores de todo o mundo. São úteis para o pesquisador depositar dados, recuperar informações e arquivos (brutos ou processados) originados de outros experimentos ou indexar artigos científicos, como PubMed. Outra possibilidade é buscar pelo termo desejado (um gene, uma proteína, uma doença, um organismo, etc.) e verificar todos os resultados relacionados a essa busca. Existem bases de dados dedicadas aos SNPs (dbSNP), ao conhecimento da caracterização dos genes e suas vias (KEGG) e à descrição da função gênica classificando-a por componente celular, função molecular e processo biológico (Gene Ontology). Além de bancos de dados que contêm informações moleculares específicas, existem outros que são amplos no sentido de armazenar informações sobre um organismo ou grupo de organismos. Como exemplo de banco de dados voltado para apenas um organismo, mas que contém muitos dados sobre ele, está o banco de dados genético e molecular Arabidopsis thaliana – TAIR. O Phytozome, por sua vez, armazena os arquivos de montagens e anotações de dezenas de genomas de plantas, contendo também ferramentas de visualização e análise. Além disso, existe uma interconexão entre algumas bases de dados na troca/compartilhamento de informações e uma iniciativa importante foi o International Nucleotide Sequence Database Collaboration (INSDC) que relaciona dados de DDBJ, EMBL-EBI e NCBI.
Atualmente, o aumento no tamanho e na complexidade dos conjuntos de dados moleculares leva ao uso de métodos estatísticos poderosos fornecidos por algoritmos da ciência da computação desenvolvidos pela área de aprendizado de máquina. Portanto, a mineração de dados e o aprendizado de máquina permitem a detecção de padrões em dados com estrutura complexa, como os biológicos, por meio de métodos de aprendizado supervisionado e não supervisionado, regressão, detecção de clusters e mineração de regras de associação, entre outros. Para indicar alguns deles, mapas auto-organizados e k-means são exemplos de algoritmos de agrupamento; implementação de redes neurais e modelos de máquinas de vetor de suporte são exemplos de algoritmos comuns de aprendizado de máquina.
O trabalho colaborativo entre biólogos moleculares, bioinformáticos, estatísticos e cientistas da computação é importante para realizar um experimento corretamente, desde o planejamento, passando pela geração e análise de dados, até a interpretação biológica dos resultados.
Uso de métodos computacionalmente intensivos
Por outro lado, o advento da tecnologia de computador moderna e recursos de computação relativamente baratos permitiram métodos bioestatísticos intensivos em computador, como métodos de bootstrapping e reamostragem.
Nos últimos tempos, as florestas aleatórias ganharam popularidade como método de classificação estatística. As técnicas florestais aleatórias geram um painel de árvores de decisão. As árvores de decisão têm a vantagem de poder desenhá-las e interpretá-las (mesmo com um conhecimento básico de matemática e estatística). Florestas aleatórias têm sido usadas para sistemas de apoio à decisão clínica.
Aplicativos
Saúde pública
Saúde pública, incluindo epidemiologia, pesquisa em serviços de saúde, nutrição, saúde ambiental e políticas e cuidados de saúde; gerenciamento. Nesses conteúdos de medicamentos, é importante considerar o desenho e a análise dos ensaios clínicos. Como exemplo, tem-se a avaliação do estado de gravidade de um paciente com prognóstico de desfecho de uma doença.
Com as novas tecnologias e conhecimentos genéticos, a bioestatística passou a ser utilizada também para a medicina de Sistemas, que consiste numa medicina mais personalizada. Para isso, é feita uma integração de dados de diferentes fontes, incluindo dados convencionais de pacientes, parâmetros clínico-patológicos, dados moleculares e genéticos, bem como dados gerados por tecnologias new-ômicas adicionais.
Genética quantitativa
O estudo da genética populacional e da genética estatística para vincular a variação no genótipo com uma variação no fenótipo. Em outras palavras, é desejável descobrir a base genética de um traço mensurável, um traço quantitativo, que esteja sob controle poligênico. Uma região do genoma que é responsável por uma característica contínua é chamada de locus de característica quantitativa (QTL). O estudo de QTLs torna-se viável pelo uso de marcadores moleculares e mensuração de características em populações, mas seu mapeamento necessita da obtenção de uma população a partir de um cruzamento experimental, como uma F2 ou linhagens/linhagens endogâmicas recombinantes (RILs). Para escanear regiões de QTLs em um genoma, um mapa genético baseado em ligação deve ser construído. Alguns dos algoritmos de mapeamento de QTL mais conhecidos são Mapeamento de intervalo, Mapeamento de intervalo composto e Mapeamento de intervalo múltiplo.
No entanto, a resolução do mapeamento de QTL é prejudicada pela quantidade de recombinação testada, um problema para espécies nas quais é difícil obter descendentes grandes. Além disso, a diversidade alélica é restrita a indivíduos originados de pais contrastantes, o que limita os estudos de diversidade alélica quando temos um painel de indivíduos representando uma população natural. Por esse motivo, o estudo de associação ampla do genoma foi proposto para identificar QTLs com base no desequilíbrio de ligação, ou seja, a associação não aleatória entre características e marcadores moleculares. Foi alavancado pelo desenvolvimento da genotipagem SNP de alto rendimento.
No melhoramento animal e vegetal, o uso de marcadores na seleção visando o melhoramento, principalmente os moleculares, colaborou para o desenvolvimento da seleção assistida por marcadores. Enquanto o mapeamento QTL é limitado devido à resolução, o GWAS não tem poder suficiente quando raras variantes de pequeno efeito também são influenciadas pelo ambiente. Assim, surge o conceito de Seleção Genômica (SG) com o objetivo de utilizar todos os marcadores moleculares na seleção e permitir a previsão do desempenho dos candidatos nesta seleção. A proposta é genotipar e fenotipar uma população de treinamento, desenvolver um modelo que possa obter os valores genéticos estimados genômicos (GEBVs) de indivíduos pertencentes a uma população de genótipo e não fenótipo, denominada população de teste. Este tipo de estudo também poderia incluir uma população de validação, pensando no conceito de validação cruzada, em que os resultados reais do fenótipo medidos nesta população são comparados com os resultados do fenótipo baseados na predição, o que serve para verificar a precisão do modelo.
Em resumo, alguns pontos sobre a aplicação da genética quantitativa são:
- Isso tem sido usado na agricultura para melhorar as culturas (criação de implantes) e gado (criação animal).
- Na pesquisa biomédica, este trabalho pode ajudar a encontrar alelos gene candidatos que podem causar ou influenciar a predisposição a doenças na genética humana.
Dados de expressão
Estudos de expressão diferencial de genes a partir de dados de RNA-Seq, como para RT-qPCR e microarrays, exigem comparação de condições. O objetivo é identificar genes que tenham uma mudança significativa na abundância entre diferentes condições. Em seguida, os experimentos são planejados adequadamente, com réplicas para cada condição/tratamento, randomização e bloqueio, quando necessário. No RNA-Seq, a quantificação da expressão utiliza as informações dos reads mapeados que estão resumidos em alguma unidade genética, como éxons que fazem parte de uma sequência gênica. Como os resultados do microarray podem ser aproximados por uma distribuição normal, os dados de contagens de RNA-Seq são melhor explicados por outras distribuições. A primeira distribuição utilizada foi a de Poisson, mas ela subestima o erro amostral, levando a falsos positivos. Atualmente, a variação biológica é considerada por métodos que estimam um parâmetro de dispersão de uma distribuição binomial negativa. Modelos lineares generalizados são usados para realizar os testes de significância estatística e como o número de genes é alto, a correção de múltiplos testes deve ser considerada. Alguns exemplos de outras análises em dados genômicos vêm de experimentos de microarray ou proteômica. Muitas vezes sobre doenças ou estágios da doença.
Outros estudos
- Ecologia, previsão ecológica
- Análise da sequência biológica
- Biologia de sistemas para inferência de rede genética ou análise de vias.
- Pesquisa clínica e desenvolvimento farmacêutico
- Dinâmica populacional, especialmente no que diz respeito à ciência da pesca.
- Filogenética e evolução
- Farmacodinâmica
- Farmacocinética
- Neuroimagem
Ferramentas
Existem muitas ferramentas que podem ser usadas para fazer análises estatísticas em dados biológicos. A maioria deles é útil em outras áreas do conhecimento, abrangendo um grande número de aplicações (alfabéticas). Aqui estão breves descrições de alguns deles:
- ASReml: Outro software desenvolvido pela VSNi que pode ser usado também no ambiente R como um pacote. É desenvolvido para estimar componentes de variância sob um modelo misto linear geral usando a probabilidade máxima restrita (REML). Modelos com efeitos fixos e efeitos aleatórios e aninhados ou cruzados são permitidos. Dá a possibilidade de investigar diferentes estruturas de matriz de variância-covariância.
- CycDesigN: Um pacote de computador desenvolvido pela VSNi que ajuda os pesquisadores a criar projetos experimentais e analisar dados provenientes de um projeto presente em uma das três classes tratadas pela CycDesigN. Estas classes são projetos resolvíveis, não-resolvíveis, parcialmente replicados e crossover. Ele inclui projetos menos utilizados os latinizados, como design t-latinizado.
- Orange: Uma interface de programação para processamento de dados de alto nível, mineração de dados e visualização de dados. Inclua ferramentas para expressão genética e genômica.
- R: Um ambiente de código aberto e linguagem de programação dedicada à computação estatística e gráficos. É uma implementação da linguagem S mantida pelo CRAN. Além de suas funções para ler tabelas de dados, tomar estatísticas descritivas, desenvolver e avaliar modelos, seu repositório contém pacotes desenvolvidos por pesquisadores em todo o mundo. Isso permite o desenvolvimento de funções escritas para lidar com a análise estatística de dados que vem de aplicações específicas. No caso da Bioinformática, por exemplo, existem pacotes localizados no repositório principal (CRAN) e em outros, como Biocondutor. Também é possível usar pacotes em desenvolvimento que são compartilhados em serviços de hospedagem como GitHub.
- SAS: Um software de análise de dados amplamente utilizado, passando por universidades, serviços e indústria. Desenvolvido por uma empresa com o mesmo nome (SAS Institute), ela usa a linguagem SAS para programação.
- POLÍTICA 3.0: É um software de análise bioestatística para ambientes regulados (por exemplo, testes de drogas) que suporta ensaios de resposta quantitativa (Parallel-Line, Parallel-Logistics, Slope-Ratio) e Ensaios Dichotomous (Resposta Quantal, Ensaios Binários). Ele também suporta métodos de ponderação para cálculos de combinação e a agregação automática de dados de ensaio independente.
- Weka: Um software Java para aprendizado de máquina e mineração de dados, incluindo ferramentas e métodos para visualização, clustering, regressão, regra de associação e classificação. Existem ferramentas para validação cruzada, bootstrapping e um módulo de comparação de algoritmos. Weka também pode ser executado em outras linguagens de programação como Perl ou R.
- Análise de imagem Python (linguagem de programação), aprendizagem profunda, machine-learning
- Bancos de dados SQL
- NoSQL
- NumPython numérico
- SciPy
- SageMath
- Álgebra linear LAPACK
- MATLABRA
- Apache Hadoop
- Apache Spark
- Amazon Web Services
Escopo e programas de treinamento
Quase todos os programas educacionais em bioestatística são em nível de pós-graduação. Eles são mais freqüentemente encontrados em escolas de saúde pública, filiadas a escolas de medicina, silvicultura ou agricultura, ou como foco de aplicação em departamentos de estatística.
Nos Estados Unidos, onde várias universidades têm departamentos de bioestatística dedicados, muitas outras universidades de primeira linha integram o corpo docente de bioestatística em estatísticas ou outros departamentos, como epidemiologia. Assim, os departamentos que levam o nome de "bioestatística" podem existir sob estruturas bastante diferentes. Por exemplo, departamentos de bioestatística relativamente novos foram fundados com foco em bioinformática e biologia computacional, enquanto departamentos mais antigos, normalmente afiliados a escolas de saúde pública, terão linhas de pesquisa mais tradicionais envolvendo estudos epidemiológicos e ensaios clínicos, bem como bioinformática. Em universidades maiores em todo o mundo, onde existem departamentos de estatística e bioestatística, o grau de integração entre os dois departamentos pode variar desde o mínimo até uma colaboração muito próxima. Em geral, a diferença entre um programa de estatística e um programa de bioestatística é dupla: (i) os departamentos de estatística geralmente abrigam pesquisas teóricas/metodológicas que são menos comuns em programas de bioestatística e (ii) os departamentos de estatística têm linhas de pesquisa que podem incluir aplicações biomédicas mas também outras áreas como a indústria (controlo de qualidade), negócios e economia e áreas biológicas que não a medicina.
Revistas especializadas
- Bioestatística
- Jornal Internacional de Bioestatística
- Revista de Epidemiologia e Bioestatística
- Bioestatística e Saúde Pública
- Biometria
- Biometrika
- Revista Biométrica
- Comunicações em Biometria e Ciência das culturas
- Aplicações estatísticas em genética e biologia molecular
- Métodos Estatísticos em Pesquisa Médica
- Estatísticas farmacêuticas
- Estatísticas em Medicina
Contenido relacionado
Doença arterial coronária
Função de distribuição cumulativa
Desmotóracido