Átomo de hidrogênio
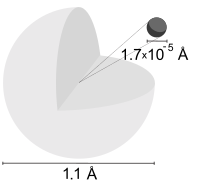
Um átomo de hidrogênio é um átomo do elemento químico hidrogênio. O átomo eletricamente neutro contém um único próton carregado positivamente e um único elétron carregado negativamente ligado ao núcleo pela força de Coulomb. O hidrogênio atômico constitui cerca de 75% da massa bariônica do universo.
Na vida cotidiana na Terra, átomos de hidrogênio isolados (chamados de "hidrogênio atômico") são extremamente raros. Em vez disso, um átomo de hidrogênio tende a se combinar com outros átomos em compostos, ou com outro átomo de hidrogênio para formar gás hidrogênio comum (diatômico), H2. "Hidrogênio atômico" e "átomo de hidrogênio" no uso comum do inglês têm significados sobrepostos, mas distintos. Por exemplo, uma molécula de água contém dois átomos de hidrogênio, mas não contém hidrogênio atômico (o que se referiria a átomos de hidrogênio isolados).
A espectroscopia atômica mostra que existe um conjunto infinito discreto de estados em que um átomo de hidrogênio (ou qualquer) pode existir, ao contrário das previsões da física clássica. As tentativas de desenvolver uma compreensão teórica dos estados do átomo de hidrogênio têm sido importantes para a história da mecânica quântica, uma vez que todos os outros átomos podem ser compreendidos de forma aproximada ao se conhecer em detalhes essa estrutura atômica mais simples.
Isótopos
O isótopo mais abundante, hidrogênio-1, prótio ou hidrogênio leve, não contém nêutrons e é simplesmente um próton e um elétron. Protium é estável e compõe 99,985% dos átomos de hidrogênio que ocorrem naturalmente.
Deutério (2H) contém um nêutron e um próton em seu núcleo. O deutério é estável e representa 0,0156% do hidrogênio natural e é usado em processos industriais como reatores nucleares e ressonância magnética nuclear.
Trítio (3H) contém dois nêutrons e um próton em seu núcleo e não é estável, decaindo com uma meia-vida de 12,32 anos. Devido à sua meia-vida curta, o trítio não existe na natureza, exceto em quantidades vestigiais.
Isótopos mais pesados de hidrogênio são criados apenas artificialmente em aceleradores de partículas e têm meias-vidas da ordem de 10−22 segundos. São ressonâncias não ligadas localizadas além da linha de gotejamento de nêutrons; isso resulta na emissão imediata de um nêutron.
As fórmulas abaixo são válidas para todos os três isótopos de hidrogênio, mas valores ligeiramente diferentes da constante de Rydberg (fórmula de correção fornecida abaixo) devem ser usados para cada isótopo de hidrogênio.
Íon de hidrogênio
Os átomos de hidrogênio neutros solitários são raros em condições normais. No entanto, o hidrogênio neutro é comum quando está ligado covalentemente a outro átomo, e os átomos de hidrogênio também podem existir nas formas catiônica e aniônica.
Se um átomo neutro de hidrogênio perde seu elétron, ele se torna um cátion. O íon resultante, que consiste apenas em um próton para o isótopo usual, é escrito como "H+" e às vezes chamado de hidron. Prótons livres são comuns no meio interestelar e no vento solar. No contexto de soluções aquosas de ácidos clássicos de Brønsted-Lowry, como o ácido clorídrico, é na verdade hidrônio, H3O+, que se entende. Em vez de um único átomo de hidrogênio ionizado literal ser formado, o ácido transfere o hidrogênio para H2O, formando H3O+.
Se, em vez disso, um átomo de hidrogênio ganhar um segundo elétron, ele se tornará um ânion. O ânion de hidrogênio é escrito como "H–" e chamado hidreto.
Análise teórica
O átomo de hidrogênio tem um significado especial na mecânica quântica e na teoria quântica de campos como um sistema físico de problema simples de dois corpos que produziu muitas soluções analíticas simples em forma fechada.
Falha na descrição clássica
Experiências de Ernest Rutherford em 1909 mostraram que a estrutura do átomo é um núcleo denso e positivo com uma tênue nuvem de carga negativa ao seu redor. Isso imediatamente levantou questões sobre como tal sistema poderia ser estável. O eletromagnetismo clássico mostrou que qualquer carga acelerada irradia energia, como mostra a fórmula de Larmor. Se for assumido que o elétron orbita em um círculo perfeito e irradia energia continuamente, o elétron espiralaria rapidamente no núcleo com um tempo de queda de:
Modelo Bohr–Sommerfeld
Em 1913, Niels Bohr obteve os níveis de energia e frequências espectrais do átomo de hidrogênio depois de fazer uma série de suposições simples para corrigir o modelo clássico falho. As suposições incluíam:
- Os electrões só podem estar em certas órbitas circulares discretas ou estados estacionários, tendo assim um conjunto discreto de possíveis raios e energias.
- Os eletrons não emitem radiação enquanto em um desses estados estacionários.
- Um elétron pode ganhar ou perder energia saltando de uma órbita discreta para outra.
Bohr supôs que o momento angular do elétron é quantizado com valores possíveis:
Para n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Não., o valor
O valor exato da constante de Rydberg assume que o núcleo é infinitamente massivo em relação ao elétron. Para hidrogênio-1, hidrogênio-2 (deutério) e hidrogênio-3 (trítio), que têm massa finita, a constante deve ser ligeiramente modificada para usar a massa reduzida do sistema, em vez de simplesmente a massa do elétron. Isso inclui a energia cinética do núcleo no problema, porque a energia cinética total (elétron mais nuclear) é equivalente à energia cinética da massa reduzida movendo-se com uma velocidade igual à velocidade do elétron em relação ao núcleo. No entanto, como o núcleo é muito mais pesado que o elétron, a massa do elétron e a massa reduzida são quase as mesmas. A constante de Rydberg RM para um átomo de hidrogênio (um elétron), R é dada por
Ainda havia problemas com o modelo de Bohr:
- não conseguiu prever outros detalhes espectrais como estrutura fina e estrutura hiperfina
- só poderia prever níveis de energia com qualquer precisão para átomos mono-eletrônicos (atoms como hidrogênio)
- os valores previstos foram apenas corretos para α α 2? ? 10.- Sim. - Sim. 5{displaystyle alfa ^{2}approx 10^{-5}}, onde α α - Sim. é a constante de estrutura fina.
A maioria dessas deficiências foi resolvida pela modificação de Arnold Sommerfeld do modelo de Bohr. Sommerfeld introduziu dois graus adicionais de liberdade, permitindo que um elétron se movesse em uma órbita elíptica caracterizada por sua excentricidade e declinação em relação a um eixo escolhido. Isso introduziu dois números quânticos adicionais, que correspondem ao momento angular orbital e sua projeção no eixo escolhido. Assim, a multiplicidade correta de estados (exceto para o fator 2 responsável pelo ainda desconhecido spin do elétron) foi encontrada. Além disso, aplicando a relatividade especial às órbitas elípticas, Sommerfeld conseguiu derivar a expressão correta para a estrutura fina dos espectros de hidrogênio (que é exatamente a mesma da mais elaborada teoria de Dirac). No entanto, alguns fenômenos observados, como o efeito Zeeman anômalo, permaneceram sem explicação. Essas questões foram resolvidas com o pleno desenvolvimento da mecânica quântica e da equação de Dirac. É frequentemente alegado que a equação de Schrödinger é superior à teoria de Bohr-Sommerfeld na descrição do átomo de hidrogênio. Este não é o caso, já que a maioria dos resultados de ambas as abordagens coincidem ou são muito próximos (uma exceção notável é o problema do átomo de hidrogênio em campos elétricos e magnéticos cruzados, que não pode ser resolvido de forma autoconsistente na estrutura de Bohr– teoria de Sommerfeld), e em ambas as teorias as principais deficiências resultam da ausência do spin do elétron. Foi o completo fracasso da teoria de Bohr-Sommerfeld em explicar sistemas de muitos elétrons (como átomo de hélio ou molécula de hidrogênio) que demonstrou sua inadequação na descrição de fenômenos quânticos.
Equação de Schrödinger
A equação de Schrödinger permite calcular os estados estacionários e também a evolução temporal dos sistemas quânticos. Respostas analíticas exatas estão disponíveis para o átomo de hidrogênio não relativístico. Antes de apresentarmos um relato formal, aqui damos uma visão geral elementar.
Dado que o átomo de hidrogênio contém um núcleo e um elétron, a mecânica quântica permite prever a probabilidade de encontrar o elétron a qualquer distância radial dada RNão.. É dado pelo quadrado de uma função matemática conhecida como a "função de onda", que é uma solução da equação de Schrödinger. O estado de equilíbrio de energia mais baixo do átomo de hidrogênio é conhecido como o estado do solo. A função de onda do estado do solo é conhecida como 1S- Sim. Função de onda. Está escrito como:
Toma. um0Não. a_{0}} é o valor numérico do raio de Bohr. A densidade de probabilidade de encontrar o elétron a uma distância RNão. em qualquer direção radial é o valor quadrado da função de onda:
O 1S- Sim. função de onda é esférica simétrica, e a área de superfície de uma casca à distância RNão. o 4D D R2{displaystyle 4pi r^{2}}, então a probabilidade total P(R)DR{displaystyle P(r),dr} do elétron estar em uma concha a uma distância RNão. e espessura DRNão. o
Acontece que este é um máximo em R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um0Não. r=a_{0}}. Ou seja, a imagem de Bohr de um elétron orbitando o núcleo no raio um0Não. a_{0}} corresponde ao raio mais provável. Na verdade, há uma probabilidade finita de que o elétron pode ser encontrado em qualquer lugar RNão., com o probabilidade indicada pelo quadrado da função de onda. Desde a probabilidade de encontrar o elétron algures. em todo o volume é a unidade, a integral de P(R)DR{displaystyle P(r),dr} é a unidade. Então dizemos que a função de onda é devidamente normalizada.
Como discutido abaixo, o estado do solo 1S- Sim. também é indicado pelos números quânticos (n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1,Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0)(n=1,ell =0,m=0)}. Os segundo estados de energia mais baixos, logo acima do estado do solo, são dados pelos números quânticos (2,0,0)(2,0,0)}, (2,1,0)- Sim.e (2,1,± ± 1){displaystyle (2,1,pm 1)}. Estas são as seguintes: n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2Não. todos os estados têm a mesma energia e são conhecidos como 2S- Sim. e 2p{displaystyle 2mathrm {p} } estados. Há uma 2S- Sim. Estado:
Um elétron no 2S- Sim. ou 2p{displaystyle 2mathrm {p} } estado é mais provável ser encontrado na segunda órbita de Bohr com energia dada pela fórmula de Bohr.
Função de onda
O Hamiltoniano do átomo de hidrogênio é o operador de energia cinética radial e a força de atração Coulomb entre o próton positivo e o elétron negativo. Usando a equação Schrödinger independente do tempo, ignorando todas as interações de spin-coupling e usando a massa reduzida μ μ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =meM/(me+M){displaystyle mu =m_{e}M/(m_{e}+M)}, a equação é escrita como:
Expandindo o laplaciano em coordenadas esféricas:
Esta é uma equação diferencial separável e parcial que pode ser resolvida em termos de funções especiais. Quando a função de onda é separada como produto de funções R(R)(R)}, Θ Θ (θ θ )Não. Theta (theta)}e Φ Φ (φ φ )Não. Phi (varphi)} três funções diferenciais independentes aparece com A e B sendo as constantes de separação:
- radial: DDR(R2DRDR)+2μ μ R2? ? 2(E+e24D D ε ε 0R)R- Sim. - Sim. AR= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle {frac {d}{dr}}left(r^{2}{frac {dR}{dr}}right)+{frac {2mu r^{2}}{hbar ^{2}}}left(E+{frac (e^{2}}{4pi varepsilon _{0}r}}right)R-AR=0}
- polar: pecado θ θ Θ Θ DDθ θ (pecado θ θ DΘ Θ Dθ θ )+Apecado2 θ θ - Sim. - Sim. B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle sin theta} }{Theta }}{frac {d}{dtheta }}left(sin theta {frac {dTheta }{dtheta }}right)+Asin ^{2}theta -B=0}
- Azimuth: 1Φ Φ D2Φ Φ Dφ φ 2+B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0.Não. {1}{Phi }}{frac {d^{2} Phi }{dvarphi ^{2}}}+ B=0.
As funções de onda de posição normalizadas, dadas em coordenadas esféricas, são:
onde:
- ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2Rnum0∗ ∗ {displaystyle rho ={2r over {na_{0}^{*}}}},
- um0∗ ∗ Não. a_{0}^{*}} é o raio de Bohr reduzido, um0∗ ∗ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =4D D ε ε 0? ? 2μ μ e2Não. a_{0}^{*}={4pi varepsilon _{0}hbar ^{2}} over {mu e^{2}}}},
- Ln- Sim. - Sim. Eu... Eu... - Sim. - Sim. 12Eu... Eu... +1(? ? )Não. L_{n-ell -1}^{2ell +1}(rho)} é um polinômio Laguerre generalizado de grau n- Sim. - Sim. Eu... Eu... - Sim. - Sim. 1- Sim.e
- YEu... Eu... m(θ θ ,φ φ )(thetavarphi)} é uma função harmônica esférica de grau Eu... Eu... - Sim. e ordem mNão.. Note que os polinômios Laguerre generalizados são definidos de forma diferente por diferentes autores. O uso aqui é consistente com as definições usadas pelo Messias e pelo Mathematica. Em outros lugares, o polinomial Laguerre inclui um fator de (n+Eu... Eu... )!(n+ell)!}, ou o polinomial Laguerre generalizada que aparece na função de onda de hidrogênio é Ln+Eu... Eu... 2Eu... Eu... +1(? ? )Não. L_{n+ell }^{2ell +1}(rho)} Em vez disso.
Os números quânticos podem assumir os seguintes valores:
- n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1,2,3,...... {displaystyle n=1,2,3,ldots } (número quântico primitivo)
- Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,1,2,...... ,n- Sim. - Sim. 1{displaystyle ell =0,1,2,ldotsn-1} (número quântico azimutal)
- m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. Eu... Eu... ,...... ,Eu... Eu... Não. m=-ellldotsell } (número quântico magnético).
Além disso, essas funções de onda são normalizadas (ou seja, a integral de seu módulo quadrado é igual a 1) e ortogonal:
As funções de onda no espaço de momento estão relacionadas com as funções de onda no espaço de posição através de uma transformada de Fourier
As soluções para a equação de Schrödinger para o hidrogênio são analíticas, fornecendo uma expressão simples para os níveis de energia do hidrogênio e, portanto, as frequências das linhas espectrais do hidrogênio e reproduziram totalmente o modelo de Bohr e foram além dele. Também produz dois outros números quânticos e a forma da função de onda do elétron ("orbital") para os vários estados quânticos possíveis, explicando assim o caráter anisotrópico das ligações atômicas.
A equação de Schrödinger também se aplica a átomos e moléculas mais complicados. Quando há mais de um elétron ou núcleo, a solução não é analítica e cálculos de computador são necessários ou suposições simplificadas devem ser feitas.
Como a equação de Schrödinger só é válida para a mecânica quântica não relativística, as soluções que ela fornece para o átomo de hidrogênio não são totalmente corretas. A equação de Dirac da teoria quântica relativística melhora essas soluções (veja abaixo).
Resultados da equação de Schrödinger
A solução da equação Schrödinger (equação de onda) para o átomo de hidrogênio usa o fato de que o potencial de Coulomb produzido pelo núcleo é isotrópico (é radialmente simétrico no espaço e só depende da distância ao núcleo). Embora o eigenfunction de energia resultante (o orbitais) não são necessariamente isotrópicos, sua dependência das coordenadas angulares segue completamente geralmente desta isotropia do potencial subjacente: os eigenstates do Hamiltoniano (isto é, os eigenstates de energia) podem ser escolhidos como eigenstates simultâneos do operador momentum angular. Isso corresponde ao fato de que o impulso angular é conservado no movimento orbital do elétron em torno do núcleo. Portanto, os eigenstates de energia podem ser classificados por dois números quânticos de momentum angular, Eu... Eu... - Sim. e mNão. (ambos são inteiros). O momentum angular número quântico Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,1,2,...... {displaystyle ell =0,1,2,ldots } determina a magnitude do impulso angular. O número quântico magnético m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. Eu... Eu... ,...... ,+Eu... Eu... Não. m=-ellldots+ell } determina a projeção do impulso angular no (arbitraramente escolhido) zangão.Não.-axis.
Além de expressões matemáticas para o impulso angular total e projeção de impulso angular de ondas, deve-se encontrar uma expressão para a dependência radial das funções de onda. É só aqui que os detalhes do 1/R- Sim. Potencial de Coulomb entrar (aderindo a polinômios Laguerre em RNão.). Isso leva a um terceiro número quântico, o número quântico principal n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1,2,3,...... {displaystyle n=1,2,3,ldots }. O número quântico principal em hidrogênio está relacionado à energia total do átomo.
Note que o valor máximo do número quântico de momentum angular é limitado pelo número quântico principal: pode ser executado apenas até n- Sim. - Sim. 1Não., i.e., Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,1,...... ,n- Sim. - Sim. 1{displaystyle ell =0,1,ldotsn-1}.
Devido à conservação do ímpeto angular, estados do mesmo Eu... Eu... - Sim. mas diferente mNão. tem a mesma energia (isso contém todos os problemas com simetria rotacional). Além disso, para o átomo de hidrogênio, estados do mesmo nNão. mas diferente Eu... Eu... - Sim. são também degenerados (ou seja, têm a mesma energia). No entanto, esta é uma propriedade específica de hidrogênio e não é mais verdadeira para átomos mais complicados que têm um potencial (eficaz) diferente da forma 1/R- Sim. (devido à presença dos elétrons internos que protegem o potencial do núcleo).
Tendo em conta a rotação do elétron adiciona um último número quântico, a projeção do impulso angular do elétron ao longo do zangão.Não.-axis, que pode assumir dois valores. Portanto, qualquer eigenstate do elétron no átomo de hidrogênio é descrito totalmente por quatro números quânticos. De acordo com as regras habituais da mecânica quântica, o estado real do elétron pode ser qualquer superposição desses estados. Isso explica também por que a escolha zangão.Não.-axis para a quantificação direcional do vetor de impulso angular é immaterial: uma órbita de dado Eu... Eu... - Sim. e m?Não. obtido para outro eixo preferido zangão.?Não. sempre pode ser representado como uma superposição adequada dos vários estados de diferentes mNão. (mas o mesmo Eu... Eu... - Sim.) que foram obtidos zangão.Não..
Resumo matemático dos autoestados do átomo de hidrogênio
Em 1928, Paul Dirac encontrou uma equação que era totalmente compatível com a relatividade especial e (como consequência) transformou a função de onda em um "Dirac spinor" incluindo "para cima" e "para baixo" componentes de spin, com pontos positivos e "negativos" energia (ou matéria e antimatéria). A solução para esta equação deu os seguintes resultados, mais precisos do que a solução de Schrödinger.
Níveis de energia
Os níveis de energia do hidrogênio, incluindo a estrutura fina (excluindo o deslocamento de Lamb e a estrutura hiperfina), são dados pela expressão de estrutura fina de Sommerfeld:
Estados coerentes
Os estados coerentes foram propostos como
Visualizando os orbitais de elétrons do hidrogênio
A imagem à direita mostra os primeiros orbitais do átomo de hidrogênio (autofunções de energia). Estas são seções transversais da densidade de probabilidade que são codificadas por cores (preto representa densidade zero e branco representa a densidade mais alta). O número quântico do momento angular (orbital) ℓ é indicado em cada coluna, usando o código de letras espectroscópicas usual (s significa ℓ = 0, p significa ℓ = 1, d significa ℓ = 2). O número quântico principal (principal) n (= 1, 2, 3,...) é marcado à direita de cada linha. Para todas as imagens, o número quântico magnético m foi definido como 0 e o plano da seção transversal é o plano xz (z é o eixo vertical). A densidade de probabilidade no espaço tridimensional é obtida girando aquela mostrada aqui em torno do eixo z.
O "estado fundamental", ou seja, o estado de menor energia, no qual o elétron geralmente se encontra, é o primeiro, o estado 1s (nível quântico principal n = 1, ℓ = 0).
As linhas pretas ocorrem em cada orbital, exceto no primeiro: esses são os nós da função de onda, ou seja, onde a densidade de probabilidade é zero. (Mais precisamente, os nós são harmônicos esféricos que aparecem como resultado da resolução da equação de Schrödinger em coordenadas esféricas.)
Os números quânticos determinam o layout desses nós. Há:
- n- Sim. - Sim. 1Não. nós totais,
- Eu... Eu... - Sim. dos quais são nós angulares:
- mNão. nós angulares andam ao redor φ φ - Sim. eixo (em Xy! avião). (A figura acima não mostra esses nós, uma vez que traça secções cruzadas através dos xz-plane.)
- Eu... Eu... - Sim. - Sim. m- Sim. (os nós angulares restantes) ocorrem no θ θ - Sim. (vertical) eixo.
- n- Sim. - Sim. Eu... Eu... - Sim. - Sim. 1- Sim. (os nós não-angulares restantes) são nós radiais.
Recursos que vão além da solução Schrödinger
Existem vários efeitos importantes que são negligenciados pela equação de Schrödinger e que são responsáveis por certos desvios pequenos, mas mensuráveis, das linhas espectrais reais das previstas:
- Embora a velocidade média do elétron em hidrogênio seja apenas 1/137 da velocidade da luz, muitos experimentos modernos são suficientemente precisos que uma explicação teórica completa requer um tratamento totalmente relativista do problema. Um tratamento relativista resulta em um aumento momentum de cerca de 1 parte em 37.000 para o elétron. Uma vez que o comprimento de onda do elétron é determinado por seu ímpeto, orbitais contendo elétrons de maior velocidade mostram contração devido aos comprimentos de onda menores.
- Mesmo quando não há campo magnético externo, no quadro inercial do elétron em movimento, o campo eletromagnético do núcleo tem um componente magnético. O spin do elétron tem um momento magnético associado que interage com este campo magnético. Este efeito também é explicado pela relatividade especial, e leva ao chamado acoplamento spin-orbit, ou seja, uma interação entre o movimento orbital do elétron em torno do núcleo e sua rotação.
Ambos os recursos (e mais) são incorporados na equação relativística de Dirac, com previsões que chegam ainda mais perto do experimento. Novamente a equação de Dirac pode ser resolvida analiticamente no caso especial de um sistema de dois corpos, como o átomo de hidrogênio. Os estados quânticos resultantes da solução agora devem ser classificados pelo número de momento angular total j (resultante do acoplamento entre o spin do elétron e o momento angular orbital). Estados do mesmo j e do mesmo n ainda são degenerados. Assim, a solução analítica direta da equação de Dirac prevê 2S(1/2) e 2P(1/2) níveis de hidrogênio para ter exatamente a mesma energia, o que está em contradição com observações (experiência de Lamb-Retherford).
- Há sempre flutuações de vácuo do campo eletromagnético, de acordo com a mecânica quântica. Devido a tais flutuações degeneração entre estados do mesmo JJ mas diferente Eu... é levantado, dando-lhes energias ligeiramente diferentes. Isso foi demonstrado no famoso experimento Lamb-Retherford e foi o ponto de partida para o desenvolvimento da teoria da eletrodinâmica quântica (que é capaz de lidar com essas flutuações de vácuo e emprega os famosos diagramas Feynman para aproximações usando a teoria da perturbação). Este efeito é agora chamado de Lamb shift.
Para esses desenvolvimentos, era essencial que a solução da equação de Dirac para o átomo de hidrogênio pudesse ser trabalhada exatamente, de modo que qualquer desvio observado experimentalmente tivesse que ser levado a sério como um sinal de falha da teoria.
Alternativas à teoria de Schrödinger
Na linguagem da mecânica matricial de Heisenberg, o átomo de hidrogênio foi resolvido pela primeira vez por Wolfgang Pauli usando uma simetria rotacional em quatro dimensões [O(4)-simetria] gerada pelo momento angular e o vetor Laplace–Runge–Lenz. Ao estender o grupo de simetria O(4) para o grupo dinâmico O(4,2), todo o espectro e todas as transições foram incorporadas em uma única representação de grupo irredutível.
Em 1979, o átomo de hidrogênio (não relativístico) foi resolvido pela primeira vez dentro da formulação integral do caminho de Feynman da mecânica quântica por Duru e Kleinert. Este trabalho ampliou muito a gama de aplicabilidade do método de Feynman.
Livros
- Griffiths, David J. (1995). Introdução à Mecânica Quântica. Prentice Hall. ISBN 0-13-111892-7. A seção 4.2 lida com o átomo de hidrogênio especificamente, mas todo o capítulo 4 é relevante.
- Kleinert, H. (2009). Integrais de Caminhos em Mecânica Quântica, Estatística, Física Polímero e Mercados Financeiros, 4a edição, Worldscibooks.com, World Scientific, Singapore (também disponível online fik.fu-berlin.de)
Contenido relacionado
Biotecnologia
Dava Sobel
Dissolver










































![{displaystyle -{frac {hbar ^{2}}{2mu }}left[{frac {1}{r^{2}}}{frac {partial }{partial r}}left(r^{2}{frac {partial psi }{partial r}}right)+{frac {1}{r^{2}sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial psi }{partial theta }}right)+{frac {1}{r^{2}sin ^{2}theta }}{frac {partial ^{2}psi }{partial varphi ^{2}}}right]-{frac {e^{2}}{4pi varepsilon _{0}r}}psi =Epsi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fed150abb1693ab2493937b669446a54865b9562)







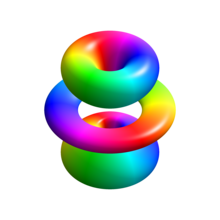






























![{displaystyle {begin{aligned}E_{j,n}={}&-mu c^{2}left[1-left(1+left[{frac {alpha }{n-j-{frac {1}{2}}+{sqrt {left(j+{frac {1}{2}}right)^{2}-alpha ^{2}}}}}right]^{2}right)^{-1/2}right]\approx {}&-{frac {mu c^{2}alpha ^{2}}{2n^{2}}}left[1+{frac {alpha ^{2}}{n^{2}}}left({frac {n}{j+{frac {1}{2}}}}-{frac {3}{4}}right)right],end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e54f0064eafaeab9e7d8b3e5e41e667a3138a7b)




![{displaystyle {begin{aligned}langle r,thetavarphi mid s,gamma{bar {Omega }}rangle ={}&e^{-s^{2}/2}sum _{n=0}^{infty }(s^{n}e^{igamma /(n+1)^{2}}/{sqrt {n!}})\&{}times ,sum _{ell =0}^{n}u_{n+1}^{ell }(r)sum _{m=-ell }^{ell }left[{frac {(2ell)!}{(ell +m)!(ell -m)!}}right]^{1/2}left(sin {frac {bar {theta }}{2}}right)^{ell -m}left(cos {frac {bar {theta }}{2}}right)^{ell +m}\&{}times ,e^{-i(m{bar {varphi }}+ell {bar {psi }})}Y_{ell m}(thetavarphi){sqrt {2ell +1}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb48ff266b61e92b9bdfcd39d562729c3910e97a)



