Ascensão certa

Ascensão direita e declinação como visto no interior da esfera celestial. A direção primária do sistema é o equinócio de março, o nó ascendente do eclíptico (vermelho) no equador celestial (azul). Ascensão direita é medida para leste até 24^h ao longo do equador celestial da direção primária.

Ascensão reta (abreviado RA; símbolo α) é a distância angular de um determinado ponto medido a leste ao longo do equador celeste desde o Sol no equinócio de março até o (círculo horário do) ponto em questão acima da Terra. Quando combinadas com a declinação, essas coordenadas astronômicas especificam a localização de um ponto na esfera celeste no sistema de coordenadas equatoriais.

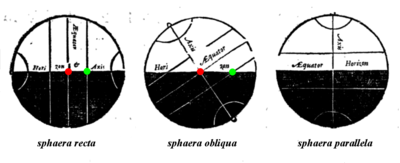
Um termo antigo, ascensão reta (latim: ascensio recta) refere-se à ascensão, ou o ponto em o equador celeste que se eleva com qualquer objeto celeste visto do equador da Terra, onde o equador celeste cruza o horizonte em um ângulo reto. Ele contrasta com a ascensão oblíqua, o ponto no equador celeste que se eleva com qualquer objeto celeste visto da maioria das latitudes da Terra, onde o equador celeste intercepta o horizonte em um ângulo oblíquo.

Explicação

Ascensão direita (azul) e declinação (verde) como visto de fora da esfera celestial

Vários ângulos de hora são representados aqui. O símbolo. marca a direção do equinócio de março.
Assumindo que o dia do ano é o equinócio de março: o Sol está em direção à seta cinzenta, a estrela marcada por uma seta verde aparecerá para subir em algum lugar no leste sobre a meia-noite (a Terra desenhada de "acima" vira anti-horário). Depois que o observador atinge a seta verde, a aurora vai sobre-poderar (ver céu azul Rayleigh espalhando) a luz da estrela por cerca de seis horas, antes de definir no horizonte ocidental. A ascensão direita da estrela é de cerca de 18^h. 18.^h significa que é uma estrela de março cedo horas e no céu azul de manhã. Secções 12^h RA, a estrela seria uma estrela de março toda a noite como em frente ao equinócio de março. 6^h RA a estrela seria uma estrela de tarde de março, em seu alto (meridiano) no crepúsculo.

A ascensão reta é o equivalente celestial da longitude terrestre. Tanto a ascensão reta quanto a longitude medem um ângulo de uma direção primária (um ponto zero) em um equador. A ascensão reta é medida a partir do Sol no equinócio de março, ou seja, o Primeiro Ponto de Áries, que é o local na esfera celeste onde o Sol cruza o equador celeste de sul a norte no equinócio de março e atualmente está localizado na constelação de Peixes. A ascensão reta é medida continuamente em um círculo completo daquele alinhamento da Terra e do Sol no espaço, aquele equinócio, a medida aumentando em direção ao leste.

Como visto da Terra (exceto nos pólos), os objetos observados com 12^h RA são os mais longos visíveis (aparecem durante a noite) no equinócio de março; aqueles com 0^h RA (além do sol) o fazem no equinócio de setembro. Nessas datas à meia-noite, tais objetos atingirão ("culminarão" em) seu ponto mais alto (seu meridiano). Quão alto depende de sua declinação; se 0° de declinação (ou seja, no equador celeste), então no equador da Terra eles estão diretamente acima (no zênite).

Qualquer unidade de medida angular poderia ter sido escolhida para a ascensão reta, mas é normalmente medida em horas (^h), minutos (^m) e segundos (^s), com 24^h sendo equivalente a um círculo completo. Os astrônomos escolheram esta unidade para medir a ascensão reta porque medem a localização de uma estrela cronometrando sua passagem pelo ponto mais alto do céu enquanto a Terra gira. A linha que passa pelo ponto mais alto do céu, chamada meridiano, é a projeção de uma linha de longitude na esfera celeste. Como um círculo completo contém 24^h de ascensão reta ou 360° (graus de arco), 1/24 de um círculo é medido como 1^h de ascensão reta, ou 15°; 1/ 1440 de um círculo é medido como 1^m de ascensão reta, ou 15 minutos de arco (também escrito como 15′); e 1/86400 de um círculo contém 1^s de ascensão reta, ou 15 segundos de arco (também escrito como 15″). Um círculo completo, medido em unidades de ascensão reta, contém 24 × 60 × 60 = 86400^s, ou 24 × 60 = 1440 ^m ou 24^h.

Como as ascensões retas são medidas em horas (de rotação da Terra), elas podem ser usadas para cronometrar as posições dos objetos no céu. Por exemplo, se uma estrela com RA = 1^h 30^m 00^s estiver em seu meridiano, então uma estrela com RA = 20^h 00^m 00^s será no/em seu meridiano (em seu ponto mais alto aparente) 18,5 horas siderais depois.

O ângulo horário sideral, usado na navegação celeste, é semelhante à ascensão reta, mas aumenta para o oeste em vez de para o leste. Geralmente medido em graus (°), é o complemento da ascensão reta em relação a 24^h. É importante não confundir o ângulo horário sideral com o conceito astronômico de ângulo horário, que mede a distância angular de um objeto a oeste do meridiano local.

Símbolos e abreviaturas

Efeitos da precessão

O eixo da Terra traça um pequeno círculo (em relação ao seu equador celeste) lentamente para o oeste sobre os pólos celestes, completando um ciclo em cerca de 26.000 anos. Esse movimento, conhecido como precessão, faz com que as coordenadas de objetos celestes estacionários mudem continuamente, embora lentamente. Portanto, as coordenadas equatoriais (incluindo a ascensão reta) são inerentemente relativas ao ano de sua observação, e os astrônomos as especificam com referência a um ano específico, conhecido como época. Coordenadas de diferentes épocas devem ser rotacionadas matematicamente para corresponder umas às outras ou para corresponder a uma época padrão. Ascensão reta para "estrelas fixas" no equador aumenta em cerca de 3,1 segundos por ano ou 5,1 minutos por século, mas para estrelas fixas longe do equador a taxa de variação pode ser qualquer coisa desde o infinito negativo até o infinito positivo. (A isso deve ser adicionado o movimento próprio de uma estrela.) Ao longo de um ciclo de precessão de 26.000 anos, "estrelas fixas" que estão longe dos pólos da eclíptica aumentam em ascensão reta em 24h, ou cerca de 5,6' por século, enquanto as estrelas dentro de 23,5° de um pólo eclíptico sofrem uma mudança líquida de 0h. A ascensão reta de Polaris está aumentando rapidamente – em 2.000 d.C. era de 2,5 horas, mas quando chegar mais perto do polo celeste norte em 2.100, sua ascensão reta será de 6 horas. O Pólo Eclíptico Norte em Draco e o Pólo Eclíptico Sul em Dorado estão sempre em ascensão reta 18^h e 6^h respectivamente.

A época padrão usada atualmente é J2000.0, que é 1º de janeiro de 2000 às 12:00 TT. O prefixo "J" indica que é uma época Juliana. Antes de J2000.0, os astrônomos usaram as sucessivas épocas Besselianas B1875.0, B1900.0 e B1950.0.

História

Como? Ascensão direita Tem o nome dele. A astronomia antiga estava muito preocupada com a ascensão e o conjunto de objetos celestiais. O Ascensão foi o ponto no equador celestial (vermelho) que subiu ou estabeleceu ao mesmo tempo como um objeto (verde) na esfera celestial. Como visto do equador, ambos estavam em um grande círculo do pólo ao pólo (esquerda, Esquema de cor ou esfera direita). De quase em qualquer outro lugar, eles não eram (centro, O que fazer? ou esfera oblíqua). Nos pólos, os objetos não subiram ou definiram (direita, Paralela de sphaera ou esfera paralela). A ascensão certa de um objeto era sua ascensão em uma esfera direita.

O conceito de ascensão reta é conhecido pelo menos desde Hiparco, que mediu estrelas em coordenadas equatoriais no século II aC. Mas Hiparco e seus sucessores fizeram seus catálogos de estrelas em coordenadas eclípticas, e o uso de RA foi limitado a casos especiais.

Com a invenção do telescópio, tornou-se possível para os astrônomos observar objetos celestes com mais detalhes, desde que o telescópio pudesse ser mantido apontado para o objeto por um período de tempo. A maneira mais fácil de fazer isso é usar uma montagem equatorial, que permite que o telescópio fique alinhado com um de seus dois pivôs paralelo ao eixo da Terra. Uma unidade de relógio motorizada geralmente é usada com uma montagem equatorial para cancelar a rotação da Terra. Como a montagem equatorial tornou-se amplamente adotada para observação, o sistema de coordenadas equatoriais, que inclui a ascensão reta, foi adotado ao mesmo tempo para simplificar. As montagens equatoriais poderiam então ser apontadas com precisão para objetos com ascensão e declinação reta conhecidas pelo uso de círculos de fixação. O primeiro catálogo de estrelas a usar ascensão reta e declinação foi a Historia Coelestis Britannica de John Flamsteed (1712, 1725).

Todo o céu, dividido em duas metades. Ascensão direita (azul) começa no equinócio de março (à direita, na interseção da eclíptica (vermelho) e do equador (verde)) e aumenta para o leste (para a esquerda). As linhas de ascensão direita (azul) do pólo ao pólo dividem o céu em 24 horas, cada equivalente a 15°.

Notas e referências