Área

Área é a medida do tamanho de uma região em uma superfície. A área de uma região plana ou área plana refere-se à área de uma forma ou lâmina planar, enquanto a área de superfície refere-se à área de uma superfície aberta ou ao limite de uma objeto tridimensional. Área pode ser entendida como a quantidade de material com uma determinada espessura que seria necessária para fazer um modelo da forma, ou a quantidade de tinta necessária para cobrir a superfície com uma única demão. É o análogo bidimensional do comprimento de uma curva (um conceito unidimensional) ou do volume de um sólido (um conceito tridimensional).

A área de uma forma pode ser medida comparando-a com quadrados de tamanho fixo. No Sistema Internacional de Unidades (SI), a unidade padrão de área é o metro quadrado (escrito como m²), que é a área de um quadrado cujos lados têm um metro de comprimento. Uma forma com uma área de três metros quadrados teria a mesma área de três desses quadrados. Em matemática, o quadrado unitário é definido como tendo área um, e a área de qualquer outra forma ou superfície é um número real adimensional.

Existem várias fórmulas conhecidas para as áreas de formas simples, como triângulos, retângulos e círculos. Usando essas fórmulas, a área de qualquer polígono pode ser encontrada dividindo o polígono em triângulos. Para formas com limite curvo, o cálculo geralmente é necessário para calcular a área. De fato, o problema de determinar a área de figuras planas foi uma das principais motivações para o desenvolvimento histórico do cálculo.

Para uma forma sólida, como uma esfera, cone ou cilindro, a área de sua superfície limite é chamada de área de superfície. As fórmulas para as áreas de superfície de formas simples foram calculadas pelos antigos gregos, mas calcular a área de superfície de uma forma mais complicada geralmente requer cálculo multivariável.

A área desempenha um papel importante na matemática moderna. Além de sua importância óbvia em geometria e cálculo, a área está relacionada à definição de determinantes em álgebra linear e é uma propriedade básica de superfícies em geometria diferencial. Na análise, a área de um subconjunto do plano é definida usando a medida de Lebesgue, embora nem todo subconjunto seja mensurável. Em geral, a área em matemática superior é vista como um caso especial de volume para regiões bidimensionais.

A área pode ser definida através do uso de axiomas, definindo-a em função de um conjunto de determinadas figuras planas ao conjunto dos números reais. Pode-se provar que tal função existe.

Definição formal

Uma abordagem para definir o que significa "área" é através de axiomas. "Área" pode ser definido como uma função de uma coleção M de tipos especiais de figuras planas (denominados conjuntos mensuráveis) para o conjunto de números reais, que satisfaz as seguintes propriedades:

• Para todos S em M, um(S≥ 0.
• Se S e T em M então assim são S Telecomunicações T e S ─ Te também um(STelecomunicaçõesT) = um(S) + um(T) um(S ─ T).
• Se S e T em M com S ⊆ T então T - Sim. S em M e um(T- Sim.S) = um(T) um(S).
• Se um conjunto S em M e S é congruente para T então T também M e um(S) = um(T).
• Cada retângulo R em M. Se o retângulo tiver comprimento h e largura k então um(R) = Hkk.
• Vamos. Q ser um conjunto fechado entre duas regiões S e T. Uma região de etapa é formada a partir de uma união finita de rectângulos adjacentes que descansam em uma base comum, ou seja,. S ⊆ Q ⊆ T. Se houver um número único c tal que um(S) ≤ c ≤ um(T) para todas as regiões desse passo S e T, então um(Q) = c.

Pode ser provado que tal função de área realmente existe.

Unidades

Quadrado de metro quadrado feito de tubo de PVC.

Cada unidade de comprimento tem uma unidade de área correspondente, ou seja, a área de um quadrado com o comprimento do lado dado. Assim, as áreas podem ser medidas em metros quadrados (m²), centímetros quadrados (cm²), milímetros quadrados (mm²), quilômetros quadrados (km²), pés quadrados (ft²), jardas quadradas (yd²), milhas quadradas (mi²), e assim por diante. Algebricamente, essas unidades podem ser consideradas como os quadrados das unidades de comprimento correspondentes.

A unidade SI de área é o metro quadrado, que é considerada uma unidade derivada do SI.

Conversões

Embora haja 10 mm em 1 cm, há 100 mm² em 1 cm².

O cálculo da área de um quadrado cujo comprimento e largura são de 1 metro seria:

1 metro × 1 metro = 1 m²

e assim, um retângulo com lados diferentes (digamos, comprimento de 3 metros e largura de 2 metros) teria uma área em unidades quadradas que pode ser calculada como:

3 metros × 2 metros = 6 m². Isso equivale a 6 milhões de milímetros quadrados. Outras conversões úteis são:

• 1 quilômetro quadrado = 1.000.000 metros quadrados
• 1 metro quadrado = 10.000 centímetros quadrados = 1.000.000 milímetros quadrados
• 1 centímetro quadrado = 100 milímetros quadrados.

Unidades não métricas

Em unidades não métricas, a conversão entre duas unidades quadradas é o quadrado da conversão entre as unidades de comprimento correspondentes.

1 pé = 12 polegadas,

a relação entre pés quadrados e polegadas quadradas é

1 pé quadrado = 144 polegadas quadrados,

onde 144 = 12² = 12 × 12. Da mesma forma:

• 1 jarda quadrada = 9 pés quadrados
• 1 milha quadrada = 3,097,600 metros quadrados = 27,878,400 pés quadrados

Além disso, os fatores de conversão incluem:

• 1 polegada quadrada = 6.4516 centímetros quadrados
• 1 pé quadrado = 0,09290304 metros quadrados
• 1 jarda quadrada = 0,3612736 metros quadrados
• 1 milha quadrada = 2.589988110336 quilômetros quadrados

Outras unidades, incluindo histórico

Existem várias outras unidades comuns para área. O are era a unidade original de área no sistema métrico, com:

• 1 são = 100 metros quadrados

Embora o are tenha caído em desuso, o hectare ainda é comumente usado para medir a terra:

• 1 hectare = 100 ares = 10.000 metros quadrados = 0,01 quilômetros quadrados

Outras unidades métricas incomuns de área incluem a tétrade, a hectade e a miríade.

O acre também é comumente usado para medir áreas de terra, onde

• 1 acre = 4,840 jardas quadradas = 43,560 pés quadrados.

Um acre é aproximadamente 40% de um hectare.

Na escala atômica, a área é medida em unidades de celeiros, de modo que:

• 1 celeiro = 10^{- 28.} Metros quadrados.

O celeiro é comumente usado para descrever a área de seção transversal de interação na física nuclear.

Na Índia,

• 20 dhurki = 1 dhur
• 20 dhur = 1 cátha
• 20 khata = 1 bigha
• 32 khata = 1 acre

História

Área do círculo

No século V aC, Hipócrates de Chios foi o primeiro a mostrar que a área de um disco (a região delimitada por um círculo) é proporcional ao quadrado de seu diâmetro, como parte de sua quadratura da lua de Hipócrates, mas não identificou a constante de proporcionalidade. Eudoxo de Cnido, também no século V aC, também descobriu que a área de um disco é proporcional ao seu raio ao quadrado.

Posteriormente, o Livro I dos Elementos de Euclides tratou da igualdade de áreas entre figuras bidimensionais. O matemático Arquimedes usou as ferramentas da geometria euclidiana para mostrar que a área dentro de um círculo é igual à de um triângulo retângulo cuja base tem o comprimento da circunferência do círculo e cuja altura é igual ao raio do círculo, em seu livro Medição de um Círculo. (A circunferência é 2πr, e a área de um triângulo é metade da base vezes a height, produzindo a área πr² para o disco.) Arquimedes aproximou o valor de π (e, portanto, a área de um círculo de raio unitário) com seu método de duplicação, no qual ele inscreveu um triângulo regular em um círculo e observou sua área, então dobrou o número de lados para dar um hexágono regular, em seguida, dobrou repetidamente o número de lados à medida que a área do polígono se aproximava cada vez mais da do círculo (e fazia o mesmo com os polígonos circunscritos).

O cientista suíço Johann Heinrich Lambert em 1761 provou que π, a razão entre a área de um círculo e seu raio quadrado, é irracional, o que significa que não é igual ao quociente de quaisquer dois números inteiros. Em 1794, o matemático francês Adrien-Marie Legendre provou que π² é irracional; isso também prova que π é irracional. Em 1882, o matemático alemão Ferdinand von Lindemann provou que π é transcendental (não a solução de qualquer equação polinomial com coeficientes racionais), confirmando uma conjectura feita por Legendre e Euler.

Área do triângulo

Heron (ou Herói) de Alexandria descobriu o que é conhecido como a fórmula de Heron para a área de um triângulo em termos de seus lados, e uma prova pode ser encontrada em seu livro, Metrica, escrito por volta de 60 EC. Foi sugerido que Arquimedes conhecia a fórmula mais de dois séculos antes, e como Metrica é uma coleção do conhecimento matemático disponível no mundo antigo, é possível que a fórmula seja anterior à referência fornecida naquele trabalho..

Em 499 Aryabhata, um grande matemático-astrônomo da era clássica da matemática indiana e da astronomia indiana, expressou a área de um triângulo como metade da base vezes a altura no Aryabhatiya (seção 2.6).

Uma fórmula equivalente à de Heron foi descoberta pelos chineses independentemente dos gregos. Foi publicado em 1247 em Shushu Jiuzhang ("Tratado Matemático em Nove Seções"), escrito por Qin Jiushao.

Área quadrilateral

No século VII EC, Brahmagupta desenvolveu uma fórmula, agora conhecida como fórmula de Brahmagupta, para a área de um quadrilátero cíclico (um quadrilátero inscrito em um círculo) em termos de seus lados. Em 1842, os matemáticos alemães Carl Anton Bretschneider e Karl Georg Christian von Staudt encontraram independentemente uma fórmula, conhecida como fórmula de Bretschneider, para a área de qualquer quadrilátero.

Área geral do polígono

O desenvolvimento das coordenadas cartesianas por René Descartes no século XVII permitiu o desenvolvimento da fórmula do agrimensor para a área de qualquer polígono com localizações de vértices conhecidas por Gauss no século XIX.

Áreas determinadas usando cálculo

O desenvolvimento do cálculo integral no final do século XVII forneceu ferramentas que poderiam ser usadas posteriormente para calcular áreas mais complicadas, como a área de uma elipse e as áreas de superfície de vários objetos tridimensionais curvos.

Fórmulas de área

Fórmulas de polígonos

Para um polígono não-intersectante (simples), as coordenadas cartesianas (xEu...,Sim.Eu...)(x_{i},y_{i})} (Eu...=0, 1,..., n-1) de quem n vértices são conhecidos, a área é dada pela fórmula do pesquisador:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12|Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0n- Sim. - Sim. 1(xEu...Sim.Eu...+1- Sim. - Sim. xEu...+1Sim.Eu...)|- Sim. Não. Biggl vert }sum _{i=0}^{n-1}(x_{i}y_{i+1}-x_{i+1}y_{i}){ Biggr vert }}

onde quando i=n-1, então i+1 é expresso como módulo n e assim refere-se a 0.

Retângulos

A área deste retângulo éEu....

A fórmula de área mais básica é a fórmula para a área de um retângulo. Dado um retângulo com comprimento l e largura w, a fórmula da área é:

A = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Eu... (retângulo).

Ou seja, a área do retângulo é o comprimento multiplicado pela largura. Como um caso especial, como l = w no caso de um quadrado, a área de um quadrado com comprimento lateral s é dado pela fórmula:

A = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S² (quare).

A fórmula para a área de um retângulo segue diretamente das propriedades básicas da área, e às vezes é tomada como uma definição ou axioma. Por outro lado, se a geometria é desenvolvida antes da aritmética, esta fórmula pode ser usada para definir a multiplicação de números reais.

Dissecção, paralelogramos e triângulos

A maioria das outras fórmulas simples para área segue o método de dissecação. Isso envolve cortar uma forma em pedaços, cujas áreas devem somar à área da forma original.

Um diagrama mostrando como um paralelogramo pode ser reorganizado na forma de um retângulo.

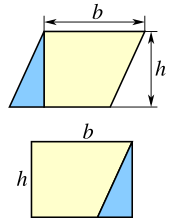
Por exemplo, qualquer paralelogramo pode ser subdividido em um trapézio e um triângulo retângulo, conforme mostrado na figura à esquerda. Se o triângulo for movido para o outro lado do trapézio, a figura resultante será um retângulo. Segue-se que a área do paralelogramo é igual à área do retângulo:

A = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Não. (paralelograma).

Um paralelograma dividido em dois triângulos iguais.

No entanto, o mesmo paralelogramo também pode ser cortado ao longo de uma diagonal em dois triângulos congruentes, conforme mostrado na figura à direita. Segue-se que a área de cada triângulo é metade da área do paralelogramo:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12b)h(1}{2}}bh} (triângulo).

Argumentos semelhantes podem ser usados para encontrar fórmulas de área para o trapézio, bem como polígonos mais complicados.

Área de formas curvas

Círculos

Um círculo pode ser dividido em setores que rearranjam para formar um paralelograma aproximado.

A fórmula para a área de um círculo (mais apropriadamente chamada de área delimitada por um círculo ou área de um disco) é baseada em um método semelhante. Dado um círculo de raio r, é possível particionar o círculo em setores, como mostra a figura à direita. Cada setor tem uma forma aproximadamente triangular e os setores podem ser reorganizados para formar um paralelogramo aproximado. A altura deste paralelogramo é r, e a largura é metade da circunferência do círculo, ou πr. Assim, a área total do círculo é πr²:

A - Sim.R² (círculo).

Embora a dissecação usada nesta fórmula seja apenas aproximada, o erro se torna cada vez menor à medida que o círculo é dividido em mais e mais setores. O limite das áreas dos paralelogramos aproximados é exatamente πr², que é a área do círculo.

Este argumento é, na verdade, uma aplicação simples das ideias do cálculo. Nos tempos antigos, o método de exaustão era usado de maneira semelhante para encontrar a área do círculo, e esse método agora é reconhecido como um precursor do cálculo integral. Usando métodos modernos, a área de um círculo pode ser calculada usando uma integral definida:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2∫ ∫ - Sim. - Sim. RRR2- Sim. - Sim. x2Dx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D D R2.Não. A;=;2int _{-r}^{r}{sqrt {r^{2}-x^{2}}},dx;=;pi r^{2}

Elipses

A fórmula da área delimitada por uma elipse está relacionada com a fórmula de um círculo; para uma elipse com semi-eixos maiores e semi-menores x e y a fórmula é:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D D xSim..A=pi xy.}

Área de superfície não plana

Arquimedes mostraram que a área de superfície de uma esfera é exatamente quatro vezes a área de um disco plano do mesmo raio, e o volume fechado pela esfera é exatamente 2/3 do volume de um cilindro da mesma altura e raio.

A maioria das fórmulas básicas para área de superfície pode ser obtida cortando superfícies e aplainando-as (consulte: superfícies desenvolvíveis). Por exemplo, se a superfície lateral de um cilindro (ou qualquer prisma) for cortada longitudinalmente, a superfície pode ser achatada em um retângulo. Da mesma forma, se um corte for feito ao longo da lateral de um cone, a superfície lateral pode ser achatada em um setor de um círculo e a área resultante calculada.

A fórmula para a área da superfície de uma esfera é mais difícil de derivar: como uma esfera tem curvatura gaussiana diferente de zero, ela não pode ser achatada. A fórmula para a área da superfície de uma esfera foi obtida pela primeira vez por Arquimedes em seu trabalho Sobre a esfera e o cilindro. A fórmula é:

A = 4πr² (esfera)

onde r é o raio da esfera. Tal como acontece com a fórmula para a área de um círculo, qualquer derivação desta fórmula usa inerentemente métodos semelhantes ao cálculo.

Fórmulas gerais

Áreas de figuras bidimensionais

Área de triângulo A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b))) h2- Sim. (bcdot h){2}}}

• Um triângulo: 12Bh(1}{2}} Bh (onde) B é qualquer lado, e h é a distância da linha em que B reside no outro vértice do triângulo). Esta fórmula pode ser usada se a altura h é conhecido. Se os comprimentos dos três lados são conhecidos então Fórmula de Heron pode ser usado: S(S- Sim. - Sim. um)(S- Sim. - Sim. b))(S- Sim. - Sim. c)(s-a)(s-b)(s-c)}}} Onde? um, b), c são os lados do triângulo, e S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12(um+b)+c){displaystyle s={tfrac {1}{2}}(a+b+c)} é metade do seu perímetro. Se um ângulo e seus dois lados incluídos forem dados, a área é 12umb)pecado⁡ ⁡ (C)(1}{2}}absin(C)} Onde? C é o ângulo dado e um e b) são os seus lados incluídos. Se o triângulo for gráfico em um plano de coordenadas, uma matriz pode ser usada e é simplificada para o valor absoluto de 12(x1Sim.2+x2Sim.3+x3Sim.1- Sim. - Sim. x2Sim.1- Sim. - Sim. x3Sim.2- Sim. - Sim. x1Sim.3)(x_{1}y_{2}+x_{2}y_{3})}. Esta fórmula também é conhecida como a fórmula sapatilha e é uma maneira fácil de resolver para a área de um triângulo de coordenadas, substituindo os 3 pontos (x)₁Sim.₁), (x)₂Sim.₂)e (x)₃Sim.₃). A fórmula sapatilha também pode ser usada para encontrar as áreas de outros polígonos quando seus vértices são conhecidos. Outra abordagem para um triângulo de coordenadas é usar cálculo para encontrar a área.
• Um polígono simples construído em uma grade de pontos de igual distância (isto é, pontos com coordenadas inteiros) de tal forma que todos os vértices do polígono são pontos de grade: Eu...+b)2- Sim. - Sim. 1Não. I+{frac Não., onde Eu... é o número de pontos de grade dentro do polígono e b) é o número de pontos de fronteira. Este resultado é conhecido como teorema de Pick.

Área em cálculo

A integração pode ser pensada como medir a área sob uma curva, definida por f(x), entre dois pontos (aqui um e b)).

A área entre dois gráficos pode ser avaliada pelo cálculo da diferença entre as integrais das duas funções

• A área entre uma curva positiva e o eixo horizontal, medida entre dois valores um e b) (b é definido como o maior dos dois valores) no eixo horizontal, é dado pela integral um para b) da função que representa a curva:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ umb)f(x)Dx.{displaystyle A=int _{a}^{b}f(x),dx.}

• A área entre os gráficos de duas funções é igual à integral de uma função, f(x), menos a integral da outra função, g(x:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ umb)(f(x)- Sim. - Sim. g(x))Dx,(f(x)-g(x),dx,} Onde? f(x)(x)} é a curva com maior valor y.

• Uma área limitada por uma função R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R(θ θ ){displaystyle r=r(theta)} expressa em coordenadas polares é:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12∫ ∫ R2Dθ θ .Não. A={1 over 2}int r^{2},dtheta.}

• A área fechada por uma curva paramétrica u→ → ())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(x()),Sim.()))(x(t),y(t)} com endpoints u→ → ()0)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =u→ → ()1){displaystyle {vec {u}}(t_{0})={vec {u}}(t_{1})} é dado pelas integrais de linha:

:: )0)1xSim.:: D)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. :: )0)1Sim.x:: D)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12:: )0)1(xSim.:: - Sim. - Sim. Sim.x:: )D){displaystyle oint _{t_{0}}^{t_{1}}x{dot {y}},dt=-oint _{t_{0}}^{t_{1}}y{dot {x}},dt={1 over 2}oint _{t_{0}}^{t_{1}}(x{dot {y}}-y{dot {x}}),dt}

ou o zangão.-componente de

12:: )0)1u→ → × × u→ → :: D).Não. {1 over 2}oint _{t_{0}}^{t_{1}}{vec {u}}times {dot {vec {u}}},dt.}

(Para detalhes, veja o teorema de Green § Área cálculo.) Este é o princípio do dispositivo mecânico de planímetro.

Área delimitada entre duas funções quadráticas

Para encontrar a área limitada entre duas funções quadráticas, subtraímos uma da outra para escrever a diferença como

f(x)- Sim. - Sim. g(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umx2+b)x+c= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um(x- Sim. - Sim. α α )(x- Sim. - Sim. β β )(x)-g(x)=ax^{2}+bx+c=a(x-alpha)(x-beta)}

onde f(x) é o limite quadrático superior e g(x) é o quadrático inferior vinculado. Defina o discriminante de f(x)-g(x) como

? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b)2- Sim. - Sim. 4umc.{displaystyle Delta =b^{2}-4ac. ?

Simplificando a fórmula integral entre os gráficos de duas funções (conforme fornecido na seção acima) e usando a fórmula de Vieta, podemos obter

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? ? ? 6um2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um6(β β - Sim. - Sim. α α )3,um≠ ≠ 0.- Sim. Não. Delta }}}{6a^{2}}}={frac {a}{6}}(beta) -alpha)^{3},qquad aneq O quê?

O acima permanece válido se uma das funções delimitadoras for linear em vez de quadrática.

Área de superfície de figuras tridimensionais

• Cone: D D R(R+R2+h2){displaystyle pi rleft(r+{sqrt {r^{2}+h^{2}}}right)}, onde R é o raio da base circular, e h é a altura. Isso também pode ser reescrito como D D R2+D D REu...{displaystyle pi r^{2}+pi rl} ou D D R(R+Eu...){displaystyle pi r(r+l),!} Onde? R é o raio e Eu... é a altura inclinada do cone. D D R2{displaystyle pi r^{2}} é a área de base enquanto D D REu...- Sim. é a superfície lateral do cone.
• Cube: 6S2{displaystyle 6s^{2}}, onde S é o comprimento de uma borda.
• Cilindro: 2D D R(R+h)(r+h)}, onde R é o raio de uma base e h é a altura. O 2D D R{displaystyle 2pi r} também pode ser reescrito como D D D- Sim., onde D é o diâmetro.
• Prisma: 2B+Ph- Sim., onde B é a área de uma base, P é o perímetro de uma base, e h é a altura do prisma.
• pirâmide: B+PL2(PL}{2}}}, onde B é a área da base, P é o perímetro da base, e L é o comprimento da inclinação.
• Prisma retangular: 2(Eu... Eu... O quê?+Eu... Eu... h+O quê?h){displaystyle 2(ell w+ell h+wh)}, onde Eu... Eu... - Sim. é o comprimento, O quê? é a largura, e h é a altura.

Fórmula geral para área de superfície

A fórmula geral para a área de superfície do gráfico de uma função continuamente diferenciada zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =f(x,Sim.),(x,y),} Onde? (x,Sim.)∈ ∈ D? ? R2(x,y)in Dsubset mathbb {R} ^{2}} e DNão. é uma região no avião xy com o limite suave:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ ∫ ∫ D(∂ ∂ f∂ ∂ x)2+(∂ ∂ f∂ ∂ Sim.)2+1DxDSim..{displaystyle A=iint _{D}{sqrt {left({frac {partial f}{partial x}}right)^{2}+left({frac {partial f}{partial y}}right)^{2}+1}},dx,dy.}

Uma fórmula ainda mais geral para a área do gráfico de uma superfície paramétrica na forma vetorial R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R(u,v),{displaystyle mathbf {r} =mathbf {r} (u,v),} Onde? R- Sim. é uma função vetorial continuamente diferenciada (u,v)∈ ∈ D? ? R2(u,v)in Dsubset mathbb {R} ^{2}} é:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ ∫ ∫ D|∂ ∂ R∂ ∂ u× × ∂ ∂ R∂ ∂ v|DuDv.{displaystyle A=iint _{D}left|{frac {partial mathbf {r} }{partial u}}times {frac {partial mathbf {r} }{partial v}}right|,du,dv.}

Lista de fórmulas

Additional common formulas for area:

Shape	Formula	Variables
Square	A = s 2 {displaystyle A=s^{2}}
Rectangle	A = a b {displaystyle A=ab}
Triangle	A = 1 2 b h {displaystyle A={frac {1}{2}}bh,!}
Triangle	A = 1 2 a b sin ⁡ ( γ ) {displaystyle A={frac {1}{2}}absin(gamma),!}
Triangle (Heron's formula)	A = s ( s − a ) ( s − b ) ( s − c ) {displaystyle A={sqrt {s(s-a)(s-b)(s-c)}},!}	s = 1 2 ( a + b + c ) {displaystyle s={tfrac {1}{2}}(a+b+c)}
Isosceles triangle	A = c 4 4 a 2 − c 2 {displaystyle A={frac {c}{4}}{sqrt {4a^{2}-c^{2}}}}
Regular triangle (equilateral triangle)	A = 3 4 a 2 {displaystyle A={frac {sqrt {3}}{4}}a^{2},!}
Rhombus/Kite	A = 1 2 d e {displaystyle A={frac {1}{2}}de}
Parallelogram	A = a h a {displaystyle A=ah_{a},!}
Trapezoid	A = ( a + c ) h 2 {displaystyle A={frac {(a+c)h}{2}},!}
Regular hexagon	A = 3 2 3 a 2 {displaystyle A={frac {3}{2}}{sqrt {3}}a^{2},!}
Regular octagon	A = 2 ( 1 + 2 ) a 2 {displaystyle A=2(1+{sqrt {2}})a^{2},!}
Regular polygon ( n {displaystyle n} sides)	A = n a r 2 = p r 2 {displaystyle A=n{frac {ar}{2}}={frac {pr}{2}}} = 1 4 n a 2 cot ⁡ ( π n ) {displaystyle quad ={tfrac {1}{4}}na^{2}cot({tfrac {pi }{n}})} = n r 2 tan ⁡ ( π n ) {displaystyle quad =nr^{2}tan({tfrac {pi }{n}})} = 1 4 n p 2 cot ⁡ ( π n ) {displaystyle quad ={tfrac {1}{4n}}p^{2}cot({tfrac {pi }{n}})} = 1 2 n R 2 sin ⁡ ( 2 π n ) {displaystyle quad ={tfrac {1}{2}}nR^{2}sin({tfrac {2pi }{n}}),!}	p = n a {displaystyle p=na } (perimeter) r = a 2 cot ⁡ ( π n ) , {displaystyle r={tfrac {a}{2}}cot({tfrac {pi }{n}}),} a 2 = r tan ⁡ ( π n ) = R sin ⁡ ( π n ) {displaystyle {tfrac {a}{2}}=rtan({tfrac {pi }{n}})=Rsin({tfrac {pi }{n}})} r : {displaystyle r:} incircle radius R : {displaystyle R:} circumcircle radius
Circle	A = π r 2 = π d 2 4 {displaystyle A=pi r^{2}={frac {pi d^{2}}{4}}} ( d = 2 r : {displaystyle d=2r:} diameter)
Circular sector	A = θ 2 r 2 = L ⋅ r 2 {displaystyle A={frac {theta }{2}}r^{2}={frac {Lcdot r}{2}},!}
Ellipse	A = π a b {displaystyle A=pi ab,!}
Integral	A = ∫ a b f ( x ) d x , f ( x ) ≥ 0 {displaystyle A=int _{a}^{b}f(x)mathrm {d} x, f(x)geq 0}
	Surface area
Sphere	A = 4 π r 2 = π d 2 {displaystyle A=4pi r^{2}=pi d^{2}}
Cuboid	A = 2 ( a b + a c + b c ) {displaystyle A=2(ab+ac+bc)}
Cylinder (incl. bottom and top)	A = 2 π r ( r + h ) {displaystyle A=2pi r(r+h)}
Cone (incl. bottom)	A = π r ( r + r 2 + h 2 ) {displaystyle A=pi r(r+{sqrt {r^{2}+h^{2}}})}
Torus	A = 4 π 2 ⋅ R ⋅ r {displaystyle A=4pi ^{2}cdot Rcdot r}
Surface of revolution	A = 2 π ∫ a b f ( x ) 1 + [ f ′ ( x ) ] 2 d x {displaystyle A=2pi int _{a}^{b}!f(x){sqrt {1+left[f'(x)right]^{2}}}mathrm {d} x} (rotation around the x-axis)

Os cálculos acima mostram como encontrar as áreas de muitas formas comuns.

As áreas de polígonos irregulares (e, portanto, arbitrários) podem ser calculadas usando a "fórmula do topógrafo" (fórmula de cadarço).

Relação da área com o perímetro

A desigualdade isoperimétrica afirma que, para uma curva fechada de comprimento L (então a região que ela envolve tem perímetro L) e para área A da região que abrange,

4D D A≤ ≤ L2,{displaystyle 4pi Aleq L^{2},}

e a igualdade vale se e somente se a curva for um círculo. Assim, um círculo tem a maior área de qualquer figura fechada com um determinado perímetro.

No outro extremo, uma figura com um determinado perímetro L poderia ter uma área arbitrariamente pequena, como ilustrado por um losango "invertido" longe arbitrariamente, de modo que dois de seus ângulos estejam arbitrariamente próximos de 0° e os outros dois estejam arbitrariamente próximos de 180°.

Para um círculo, a razão entre a área e a circunferência (o termo para o perímetro de um círculo) é igual à metade do raio r. Isso pode ser visto na fórmula da área πr² e na fórmula da circunferência 2πr.

A área de um polígono regular é metade do seu perímetro vezes o apótema (onde o apótema é a distância do centro ao ponto mais próximo de qualquer lado).

Fractais

Dobrar os comprimentos das arestas de um polígono multiplica sua área por quatro, que é dois (a razão entre o novo e o antigo comprimento do lado) elevado à potência de dois (a dimensão do espaço em que o polígono reside). Mas se os comprimentos unidimensionais de um fractal desenhado em duas dimensões forem todos dobrados, o conteúdo espacial das escalas fractais por uma potência de dois que não é necessariamente um número inteiro. Esse poder é chamado de dimensão fractal do fractal.

Bissetrizes de área

Há uma infinidade de linhas que dividem a área de um triângulo. Três deles são as medianas do triângulo (que conectam os pontos médios dos lados com os vértices opostos), e estes são concorrentes no centróide do triângulo; na verdade, elas são as únicas bissetrizes de área que passam pelo centróide. Qualquer linha através de um triângulo que divida a área do triângulo e seu perímetro ao meio passa pelo incentro do triângulo (o centro de seu círculo interno). Há um, dois ou três deles para qualquer triângulo.

Qualquer linha que passa pelo ponto médio de um paralelogramo divide a área ao meio.

Todas as bissetrizes de um círculo ou outra elipse passam pelo centro e quaisquer cordas que passam pelo centro dividem a área. No caso de um círculo são os diâmetros do círculo.

Otimização

Dado um contorno de fio, a superfície de menor extensão de área ("preenchimento") é uma superfície mínima. Exemplos familiares incluem bolhas de sabão.

A questão da área de preenchimento do círculo riemanniano permanece em aberto.

O círculo tem a maior área de qualquer objeto bidimensional com o mesmo perímetro.

Um polígono cíclico (um inscrito em um círculo) tem a maior área de qualquer polígono com um determinado número de lados com os mesmos comprimentos.

Uma versão da desigualdade isoperimétrica para triângulos afirma que o triângulo de maior área entre todos aqueles com um determinado perímetro é equilátero.

O triângulo de maior área de todos os inscritos em um círculo dado é equilátero; e o triângulo de menor área de todos os circunscritos a um círculo dado é equilátero.

A proporção da área do incírculo para a área de um triângulo equilátero, D D 33Não. ? {3}}}, é maior do que o de qualquer triângulo não-equilateral.

A proporção da área ao quadrado do perímetro de um triângulo equilátero, 1123,{displaystyle {frac {1}{12{sqrt {3}}}}} é maior do que isso para qualquer outro triângulo.