Análise de variação

Análise de variância (ANOVA) é uma coleção de modelos estatísticos e seus procedimentos de estimativa associados (como a "variação" entre grupos ) usado para analisar as diferenças entre as médias. ANOVA foi desenvolvida pelo estatístico Ronald Fisher. ANOVA é baseada na lei da variância total, onde a variância observada em uma determinada variável é particionada em componentes atribuíveis a diferentes fontes de variação. Em sua forma mais simples, a ANOVA fornece um teste estatístico para saber se duas ou mais médias populacionais são iguais e, portanto, generaliza o teste t além de duas médias. Em outras palavras, a ANOVA é usada para testar a diferença entre duas ou mais médias.

História

Embora a análise de variância tenha se concretizado no século 20, os antecedentes se estendem por séculos no passado, de acordo com Stigler. Estes incluem testes de hipóteses, a partição de somas de quadrados, técnicas experimentais e o modelo aditivo. Laplace estava realizando testes de hipóteses na década de 1770. Por volta de 1800, Laplace e Gauss desenvolveram o método dos mínimos quadrados para combinar observações, que melhorou os métodos então usados em astronomia e geodésia. Também iniciou muitos estudos das contribuições para somas de quadrados. Laplace sabia como estimar uma variância a partir de uma soma de quadrados residual (em vez de total). Em 1827, Laplace estava usando métodos de mínimos quadrados para resolver problemas de ANOVA relativos a medições de marés atmosféricas. Antes de 1800, os astrônomos haviam isolado erros observacionais resultantes dos tempos de reação (a "equação pessoal") e desenvolveu métodos para reduzir os erros. Os métodos experimentais usados no estudo da equação pessoal foram posteriormente aceitos pelo campo emergente da psicologia, que desenvolveu fortes métodos experimentais (fatorial completo) aos quais a randomização e o cegamento foram logo adicionados. Uma eloquente explicação não matemática do modelo de efeitos aditivos estava disponível em 1885.

Ronald Fisher introduziu o termo variância e propôs sua análise formal em um artigo de 1918 A correlação entre parentes na suposição de herança mendeliana. Sua primeira aplicação da análise de variância foi publicada em 1921. A análise de variância tornou-se amplamente conhecida depois de ser incluída no livro de Fisher, de 1925, Statistical Methods for Research Workers.

Modelos de randomização foram desenvolvidos por vários pesquisadores. O primeiro foi publicado em polonês por Jerzy Neyman em 1923.

Exemplo

No fit: Jovem vs velho, e de cabelo curto vs longo

Ajuste justo: animal de estimação vs raça de trabalho e menos atlético vs mais atlético

Muito bom ajuste: Peso por raça

A análise de variância pode ser usada para descrever relações complexas entre variáveis. Uma exposição de cães fornece um exemplo. Uma exposição de cães não é uma amostragem aleatória da raça: ela é tipicamente limitada a cães adultos, de raça pura e exemplares. Um histograma de pesos de cães de um show pode ser bastante complexo, como a distribuição amarelo-laranja mostrada nas ilustrações. Suponha que quiséssemos prever o peso de um cão com base em um determinado conjunto de características de cada cão. Uma maneira de fazer isso é explicar a distribuição de pesos dividindo a população canina em grupos com base nessas características. Um agrupamento bem-sucedido dividirá os cães de forma que (a) cada grupo tenha uma baixa variação de pesos de cães (o que significa que o grupo é relativamente homogêneo) e (b) a média de cada grupo seja distinta (se dois grupos tiverem a mesma média, então não é razoável concluir que os grupos são, de fato, separados de forma significativa).

Nas ilustrações à direita, os grupos são identificados como X₁, X₂, etc. Na primeira ilustração, os cães são divididos de acordo com o produto (interação) de dois agrupamentos binários: jovens x velhos e de pêlo curto x de pêlo comprido (por exemplo, grupo 1 é jovem, cães de pêlo curto, grupo 2 é jovem , cães de pêlo comprido, etc.). Como as distribuições de peso dos cães dentro de cada um dos grupos (mostrado em azul) têm uma variação relativamente grande e como as médias são muito semelhantes entre os grupos, agrupar os cães por essas características não produz uma maneira eficaz de explicar a variação nos pesos dos cães : saber em que grupo um cão está não nos permite prever seu peso muito melhor do que simplesmente saber que o cão está em uma exposição canina. Assim, esse agrupamento não consegue explicar a variação da distribuição geral (amarelo-laranja).

Uma tentativa de explicar a distribuição de peso agrupando cães como raça de estimação versus raça de trabalho e menos atlético versus mais atlético provavelmente seria um pouco mais bem-sucedida (ajuste justo). Os cães de exposição mais pesados provavelmente são raças grandes, fortes e de trabalho, enquanto as raças mantidas como animais de estimação tendem a ser menores e, portanto, mais leves. Como mostra a segunda ilustração, as distribuições têm variâncias consideravelmente menores do que no primeiro caso, e as médias são mais distinguíveis. No entanto, a sobreposição significativa de distribuições, por exemplo, significa que não podemos distinguir X₁ e X₂ de forma confiável . Agrupar cães de acordo com o lançamento de uma moeda pode produzir distribuições semelhantes.

Uma tentativa de explicar o peso por raça provavelmente produzirá um ajuste muito bom. Todos os Chihuahuas são leves e todos os São Bernardos são pesados. A diferença de peso entre Setters e Pointers não justifica raças separadas. A análise de variância fornece as ferramentas formais para justificar esses julgamentos intuitivos. Um uso comum do método é a análise de dados experimentais ou o desenvolvimento de modelos. O método tem algumas vantagens sobre a correlação: nem todos os dados devem ser numéricos e um resultado do método é um julgamento da confiança em uma relação explicativa.

Classes de modelos

Existem três classes de modelos usados na análise de variância, e eles são descritos aqui.

Modelos de efeitos fixos

O modelo de efeitos fixos (classe I) de análise de variância se aplica a situações em que o experimentador aplica um ou mais tratamentos aos sujeitos do experimento para ver se os valores das variáveis de resposta mudam. Isso permite que o experimentador estime os intervalos de valores de variáveis de resposta que o tratamento geraria na população como um todo.

Efeitos fixos vs Efeitos aleatórios

Modelos de efeitos aleatórios

O modelo de efeitos aleatórios (classe II) é usado quando os tratamentos não são fixos. Isso ocorre quando os vários níveis de fator são amostrados de uma população maior. Como os próprios níveis são variáveis aleatórias, algumas suposições e o método de contraste dos tratamentos (uma generalização multivariável de diferenças simples) diferem do modelo de efeitos fixos.

Modelos de efeitos mistos

Um modelo de efeitos mistos (classe III) contém fatores experimentais de tipos de efeitos fixos e aleatórios, com interpretações e análises apropriadamente diferentes para os dois tipos.

Exemplo

As experiências de ensino podem ser realizadas por um departamento de faculdade ou universidade para encontrar um bom livro didático introdutório, com cada texto considerado um tratamento. O modelo de efeitos fixos compararia uma lista de textos candidatos. O modelo de efeitos aleatórios determinaria se existem diferenças importantes entre uma lista de textos selecionados aleatoriamente. O modelo de efeitos mistos compararia os textos titulares (fixos) com alternativas selecionadas aleatoriamente.

Definir efeitos fixos e aleatórios tem se mostrado evasivo, com definições concorrentes levando a um pântano linguístico.

Suposições

A análise de variância tem sido estudada a partir de várias abordagens, sendo a mais comum a utilização de um modelo linear que relaciona a resposta aos tratamentos e bloqueios. Observe que o modelo é linear nos parâmetros, mas pode ser não linear nos níveis de fator. A interpretação é fácil quando os dados são balanceados entre os fatores, mas uma compreensão muito mais profunda é necessária para dados desbalanceados.

Análise de livro didático usando uma distribuição normal

A análise de variância pode ser apresentada em termos de um modelo linear, que faz as seguintes suposições sobre a distribuição de probabilidade das respostas:

• Independência de observações – esta é uma suposição do modelo que simplifica a análise estatística.
• Normalidade – as distribuições dos resíduos são normais.
• A igualdade (ou "homogeneidade") de variâncias, chamada homoscedasticidade - a variância de dados em grupos deve ser a mesma.

As suposições separadas do modelo de livro implicam que os erros são independentemente, de forma idêntica e normalmente distribuídos para modelos de efeitos fixos, ou seja, que os erros (ε ε - Sim.) são independentes e

ε ε ∼ ∼ N(0,σ σ 2).{\displaystyle \varepsilon \thicksim N(0,\sigma ^{2}). ?

Análise baseada em randomização

Em um experimento controlado randomizado, os tratamentos são distribuídos aleatoriamente em unidades experimentais, seguindo o protocolo experimental. Essa randomização é objetiva e declarada antes da realização do experimento. A atribuição aleatória objetiva é usada para testar a significância da hipótese nula, seguindo as ideias de C. S. Peirce e Ronald Fisher. Esta análise baseada em design foi discutida e desenvolvida por Francis J. Anscombe na Rothamsted Experimental Station e por Oscar Kempthorne na Iowa State University. Kempthorne e seus alunos fazem uma suposição de aditividade de tratamento de unidade, que é discutida nos livros de Kempthorne e David R. Cox.

Aditividade unidade-tratamento

Em sua forma mais simples, a suposição de aditividade de tratamento unitário afirma que a resposta observada Sim.Eu...,JJ{\displaystyle y_{i,j}} de unidade experimental Eu...Não. ao receber tratamento JJNão. pode ser escrito como a soma da resposta da unidade Sim.Eu...Não. y_{i}} e o efeito do tratamento )JJ{\displaystyle t_{j}}, isto é

Sim.Eu...,JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Sim.Eu...+)JJ.Não. y_{i,j}=y_{i}+t_{j}.}

JJNão.

JJNão.

)JJ{\displaystyle t_{j}}

A suposição de aditividade de tratamento de unidade geralmente não pode ser falsificada diretamente, de acordo com Cox e Kempthorne. No entanto, muitas consequências da aditividade da unidade de tratamento podem ser falsificadas. Para um experimento aleatório, a suposição de aditividade unidade-tratamento implica que a variância é constante para todos os tratamentos. Portanto, por contraposição, uma condição necessária para a aditividade da unidade de tratamento é que a variância seja constante.

O uso de aditividade e randomização de tratamento de unidade é semelhante à inferência baseada em design que é padrão em amostragem de pesquisa de população finita.

Modelo linear derivado

Kempthorne usa a distribuição aleatória e a suposição de aditividade de tratamento unitário para produzir um modelo linear derivado, muito semelhante ao modelo de livro didático discutido anteriormente. As estatísticas de teste deste modelo linear derivado são aproximadas pelas estatísticas de teste de um modelo linear normal apropriado, de acordo com teoremas de aproximação e estudos de simulação. No entanto, existem diferenças. Por exemplo, a análise baseada em randomização resulta em uma correlação pequena, mas (estritamente) negativa entre as observações. Na análise baseada em randomização, não há suposição de uma distribuição normal e certamente nenhuma suposição de independência. Pelo contrário, as observações são dependentes!

A análise baseada em randomização tem a desvantagem de que sua exposição envolve álgebra tediosa e muito tempo. Uma vez que a análise baseada em randomização é complicada e aproximada pela abordagem que usa um modelo linear normal, a maioria dos professores enfatiza a abordagem do modelo linear normal. Poucos estatísticos se opõem à análise baseada em modelos de experimentos aleatórios balanceados.

Modelos estatísticos para dados observacionais

No entanto, quando aplicada a dados de experimentos não randomizados ou estudos observacionais, a análise baseada em modelo carece da garantia de randomização. Para dados observacionais, a derivação de intervalos de confiança deve usar modelos subjetivos, conforme enfatizado por Ronald Fisher e seus seguidores. Na prática, as estimativas dos efeitos do tratamento de estudos observacionais geralmente são inconsistentes. Na prática, "modelos estatísticos" e dados observacionais são úteis para sugerir hipóteses que devem ser tratadas com muita cautela pelo público.

Resumo das suposições

A análise ANOVA baseada em modelo normal assume a independência, normalidade e homogeneidade das variâncias dos resíduos. A análise baseada em randomização assume apenas a homogeneidade das variâncias dos resíduos (como consequência da aditividade unidade-tratamento) e usa o procedimento de randomização do experimento. Ambas as análises requerem homocedasticidade, como pressuposto para a análise de modelo normal e como consequência da randomização e aditividade para a análise baseada em randomização.

No entanto, estudos de processos que alteram variâncias em vez de médias (chamados efeitos de dispersão) foram conduzidos com sucesso usando ANOVA. Não há nenhuma suposição necessária para ANOVA em sua generalidade completa, mas o teste F usado para o teste de hipótese ANOVA tem suposições e práticas limitações que são de interesse contínuo.

Problemas que não satisfazem as suposições da ANOVA podem frequentemente ser transformados para satisfazer as suposições. A propriedade de aditividade de unidade de tratamento não é invariável sob uma "mudança de escala", então os estatísticos costumam usar transformações para alcançar a aditividade de unidade de tratamento. Se for esperado que a variável de resposta siga uma família paramétrica de distribuições de probabilidade, então o estatístico pode especificar (no protocolo para o experimento ou estudo observacional) que as respostas sejam transformadas para estabilizar a variância. Além disso, um estatístico pode especificar que as transformações logarítmicas sejam aplicadas às respostas, que se acredita seguirem um modelo multiplicativo. De acordo com o teorema da equação funcional de Cauchy, o logaritmo é a única transformação contínua que transforma a multiplicação real em adição.

Características

ANOVA é usada na análise de experimentos comparativos, aqueles em que apenas a diferença nos resultados é de interesse. A significância estatística do experimento é determinada por uma razão de duas variâncias. Essa razão é independente de várias alterações possíveis nas observações experimentais: Adicionar uma constante a todas as observações não altera a significância. Multiplicar todas as observações por uma constante não altera a significância. Portanto, o resultado da significância estatística ANOVA é independente do viés constante e dos erros de escala, bem como das unidades usadas para expressar as observações. Na era do cálculo mecânico, era comum subtrair uma constante de todas as observações (quando equivalente a descartar os dígitos iniciais) para simplificar a entrada de dados. Este é um exemplo de codificação de dados.

Lógica

Os cálculos de ANOVA podem ser caracterizados como o cálculo de um número de médias e variâncias, dividindo duas variâncias e comparando a razão com um valor manual para determinar a significância estatística. Calcular o efeito de um tratamento é então trivial: "o efeito de qualquer tratamento é estimado tomando a diferença entre a média das observações que recebem o tratamento e a média geral".

Partição da soma dos quadrados

ANOVA usa terminologia tradicional padronizada. A equação definição da variância da amostra é S2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n- Sim. - Sim. 1Gerenciamento Gerenciamento Eu...(Sim.Eu...- Sim. - Sim. Sim.? ? )2{\textstyle s^{2}={\frac {1}{n-1}}\sum _{i}(y_{i}-{\bar {y}})^{2}}, onde o divisor é chamado de graus de liberdade (DF), a soma é chamada a soma de quadrados (SS), o resultado é chamado de quadrado médio (MS) e os termos quadrados são desvios da média da amostra. ANOVA estima 3 variações de amostra: uma variância total baseada em todos os desvios de observação da grande média, uma variância de erro baseada em todos os desvios de observação de seus meios de tratamento apropriados e uma variância de tratamento. A variância do tratamento é baseada nos desvios do tratamento significa da grande média, o resultado sendo multiplicado pelo número de observações em cada tratamento para explicar a diferença entre a variância das observações e a variância dos meios.

A técnica fundamental é uma partição da soma total dos quadrados SS em componentes relacionados aos efeitos usados no modelo. Por exemplo, o modelo para uma ANOVA simplificada com um tipo de tratamento em diferentes níveis.

SSTotal= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =SSErro+SSTratamentosNão. SS_{\text{Total}}=SS_{\text{Error}}+SS_{\text{Treatments}}}

O número de graus de liberdade DF pode ser particionado de maneira semelhante: um desses componentes (o de erro) especifica uma distribuição qui-quadrada que descreve a soma de quadrados associada, enquanto o o mesmo vale para "tratamentos" se não houver efeito do tratamento.

DFTotal= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =DFErro+DFTratamentosNão. DF_{\text{Total}}=DF_{\text{Error}}+DF_{\text{Treatments}}}

O teste F

O teste F é usado para comparar os fatores do desvio total. Por exemplo, em um fator único ou ANOVA de fator único, a significância estatística é testada comparando a estatística do teste F

F= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =variância entre tratamentosvariância dentro de tratamentos{\displaystyle F={\frac {\text{variância entre tratamentos}}{\text{variância dentro de tratamentos}}}}}}}}

F= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =MSTratamentosMSErro= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =SSTratamentos/(Eu...- Sim. - Sim. 1)SSErro/(nT- Sim. - Sim. Eu...)- Sim. {MS_{\text{Treatments}}}{MS_{\text{Error}}}}={SS_{\text{Treatments}}/(I-1)} \over {SS_{\text{Error}}/(n_{T}-I)}}}}

Onde? MS é quadrado médio, Eu...Não. Eu... é o número de tratamentos e nTNão. n_{T}} é o número total de casos

ao F-distribuição com Eu...- Sim. - Sim. 1Não. Eu..., nT- Sim. - Sim. Eu...Não. N_{T}-I graus de liberdade. Usando o F-a distribuição é um candidato natural porque a estatística do teste é a proporção de duas somas dimensionadas de quadrados cada uma das quais segue uma distribuição qui-quadrado em escala.

O valor esperado de F é 1+nσ σ Tratamento2/σ σ Erro2{\displaystyle 1+{n\sigma _{\text{Treatment}}^{2}}/{\sigma _{\text{Error}}^{2}}} (onde) nNão. é o tamanho da amostra de tratamento) que é 1 para nenhum efeito de tratamento. Como os valores de F aumentam acima de 1, a evidência é cada vez mais inconsistente com a hipótese nula. Dois métodos experimentais aparentes de aumento de F estão aumentando o tamanho da amostra e reduzindo a variância de erro por controles experimentais apertados.

Existem dois métodos para concluir o teste de hipótese ANOVA, ambos produzindo o mesmo resultado:

• O método do livro é comparar o valor observado de F com o valor crítico de F determinado a partir de tabelas. O valor crítico de F é uma função dos graus de liberdade do numerador e do denominador e do nível de significância (α). Se F ≥ F_Crítica, a hipótese nula é rejeitada.
• O método do computador calcula a probabilidade (p-valor) de um valor de F maior ou igual ao valor observado. A hipótese nula é rejeitada se essa probabilidade for menor ou igual ao nível de significância (α).

O teste ANOVA F é conhecido por ser quase ideal no sentido de minimizar erros falsos negativos para uma taxa fixa de erros falsos positivos (ou seja, maximizar o poder para um nível de significância fixo). Por exemplo, para testar a hipótese de que vários tratamentos médicos têm exatamente o mesmo efeito, os valores p do teste F aproximam-se bastante dos valores p do teste de permutação: A aproximação é particularmente próximo quando o design é equilibrado. Tais testes de permutação caracterizam testes com poder máximo contra todas as hipóteses alternativas, conforme observado por Rosenbaum. O teste ANOVA F (da hipótese nula de que todos os tratamentos têm exatamente o mesmo efeito) é recomendado como um teste prático, devido à sua robustez contra muitas distribuições alternativas.

Lógica estendida

ANOVA consiste em partes separáveis; fontes de partição de variância e teste de hipótese podem ser usados individualmente. ANOVA é usada para dar suporte a outras ferramentas estatísticas. A regressão é usada primeiro para ajustar modelos mais complexos aos dados, então ANOVA é usada para comparar modelos com o objetivo de selecionar modelos simples(r) que descrevam adequadamente os dados. "Tais modelos podem ser ajustados sem qualquer referência à ANOVA, mas as ferramentas ANOVA podem então ser usadas para dar algum sentido aos modelos ajustados e para testar hipóteses sobre lotes de coeficientes." "[Nós] pensamos na análise de variância como uma forma de entender e estruturar modelos multiníveis - não como uma alternativa à regressão, mas como uma ferramenta para resumir inferências complexas de alta dimensão..."

Para um único fator

O experimento mais simples adequado para análise ANOVA é o experimento completamente aleatório com um único fator. Experimentos mais complexos com um único fator envolvem restrições na randomização e incluem blocos completamente aleatórios e quadrados latinos (e variantes: quadrados greco-latinos, etc.). Os experimentos mais complexos compartilham muitas das complexidades de múltiplos fatores. Uma discussão relativamente completa da análise (modelos, resumos de dados, tabela ANOVA) do experimento completamente aleatório está disponível.

Existem algumas alternativas para a análise de variância unidirecional convencional, por exemplo: teste F heterocedástico de Welch, teste F heterocedástico de Welch com médias aparadas e variâncias Winsorizadas, teste Brown-Forsythe, Alexander-Govern teste, teste de segunda ordem de James e teste de Kruskal-Wallis, disponível em onewaytests R

É útil representar cada ponto de dados da seguinte forma, chamada de modelo estatístico:

YEu...JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ +? ? JJ+ε ε Eu...JJNão. Sim. +\tau _{j}+\varepsilon _{ij}}

• Eu... = 1, 2, 3,..., R
• JJ = 1, 2, 3,..., C
• μ = média geral (média)
• ?_JJ = efeito diferencial (resposta) associado ao JJ nível de X;
  isto assume que, globalmente, os valores de ?_JJ adicionar a zero (isto é, Gerenciamento Gerenciamento JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1C? ? JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{\textstyle \sum _{j=1}^{C}\tau _{j}=0}})
• ε_ij = ruído ou erro associado ao particular ij valor de dados

Isto é, imaginamos um modelo aditivo que diz que cada ponto de dados pode ser representado pela soma de três quantidades: a média verdadeira, média de todos os níveis de fator sendo investigados, mais um componente incremental associado à coluna específica (nível de fator), mais um componente final associado a tudo o mais que afeta esse valor de dados específico.

Para vários fatores

ANOVA generaliza para o estudo dos efeitos de múltiplos fatores. Quando o experimento inclui observações em todas as combinações de níveis de cada fator, ele é denominado fatorial. Os experimentos fatoriais são mais eficientes do que uma série de experimentos de fator único e a eficiência cresce à medida que o número de fatores aumenta. Consequentemente, os planejamentos fatoriais são muito usados.

O uso de ANOVA para estudar os efeitos de múltiplos fatores tem uma complicação. Em uma ANOVA de 3 fatores com fatores x, y e z, o modelo ANOVA inclui termos para os efeitos principais (x, y, z) e termos para interações (xy, xz, yz, xyz). Todos os termos requerem testes de hipótese. A proliferação de termos de interação aumenta o risco de que algum teste de hipótese produza um falso positivo por acaso. Felizmente, a experiência diz que as interações de alta ordem são raras. A capacidade de detectar interações é uma grande vantagem da ANOVA de múltiplos fatores. Testar um fator por vez oculta as interações, mas produz resultados experimentais aparentemente inconsistentes.

Aconselha-se cautela ao encontrar interações; Teste os termos de interação primeiro e expanda a análise além da ANOVA se as interações forem encontradas. Os textos variam em suas recomendações sobre a continuação do procedimento ANOVA após encontrar uma interação. As interações complicam a interpretação dos dados experimentais. Nem os cálculos de significância nem os efeitos estimados do tratamento podem ser considerados pelo valor de face. "Uma interação significativa geralmente mascara a importância dos efeitos principais." Métodos gráficos são recomendados para melhorar a compreensão. A regressão costuma ser útil. Uma longa discussão sobre interações está disponível em Cox (1958). Algumas interações podem ser removidas (por transformações), enquanto outras não.

Várias técnicas são usadas com ANOVA de múltiplos fatores para reduzir despesas. Uma técnica usada em planejamentos fatoriais é minimizar a replicação (possivelmente nenhuma replicação com suporte de truques analíticos) e combinar grupos quando os efeitos forem considerados estatisticamente (ou praticamente) insignificantes. Um experimento com muitos fatores insignificantes pode colapsar em um com poucos fatores suportados por muitas replicações.

Análise associada

Algumas análises são necessárias para apoiar o desenho do experimento, enquanto outras análises são realizadas após mudanças nos fatores serem formalmente encontradas para produzir mudanças estatisticamente significativas nas respostas. Como a experimentação é iterativa, os resultados de uma experiência alteram os planos para as experiências seguintes.

Análise preparatória

O número de unidades experimentais

No projeto de um experimento, o número de unidades experimentais é planejado para satisfazer os objetivos do experimento. A experimentação é muitas vezes sequencial.

Os primeiros experimentos são frequentemente projetados para fornecer estimativas imparciais dos efeitos do tratamento e do erro experimental. Experimentos posteriores geralmente são planejados para testar a hipótese de que o efeito de um tratamento tem uma magnitude importante; neste caso, o número de unidades experimentais é escolhido para que o experimento fique dentro do orçamento e tenha potência adequada, entre outros objetivos.

Relatar a análise do tamanho da amostra geralmente é necessário em psicologia. "Forneça informações sobre o tamanho da amostra e o processo que levou às decisões sobre o tamanho da amostra." A análise, que está escrita no protocolo experimental antes da realização do experimento, é examinada em solicitações de subsídios e conselhos administrativos de revisão.

Além da análise de poder, existem métodos menos formais para selecionar o número de unidades experimentais. Estes incluem métodos gráficos baseados na limitação da probabilidade de erros falsos negativos, métodos gráficos baseados em um aumento de variação esperado (acima dos resíduos) e métodos baseados na obtenção de um intervalo de confiança desejado.

Análise de potência

A análise de poder é frequentemente aplicada no contexto da ANOVA para avaliar a probabilidade de rejeitar com sucesso a hipótese nula se assumirmos um determinado design de ANOVA, tamanho do efeito na população, tamanho da amostra e nível de significância. A análise de poder pode ajudar no desenho do estudo, determinando qual tamanho de amostra seria necessário para ter uma chance razoável de rejeitar a hipótese nula quando a hipótese alternativa for verdadeira.

Tamanho do efeito

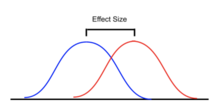
Tamanho do efeito

Várias medidas padronizadas de efeito foram propostas para ANOVA para resumir a força da associação entre um(s) preditor(es) e a variável dependente ou a diferença padronizada geral do modelo completo. As estimativas de tamanho de efeito padronizadas facilitam a comparação de descobertas entre estudos e disciplinas. No entanto, embora os tamanhos de efeito padronizados sejam comumente usados em grande parte da literatura profissional, uma medida não padronizada de tamanho de efeito que tem significado imediato "significativo" unidades podem ser preferíveis para fins de relatório.

Confirmação do modelo

Às vezes, são realizados testes para determinar se as suposições da ANOVA parecem ter sido violadas. Os resíduos são examinados ou analisados para confirmar a homocedasticidade e normalidade bruta. Resíduos devem ter a aparência de ruído (distribuição normal média zero) quando plotados como uma função de qualquer coisa, incluindo tempo e valores de dados modelados. As tendências sugerem interações entre fatores ou entre observações.

Testes de acompanhamento

Um efeito estatisticamente significativo em ANOVA geralmente é seguido por testes adicionais. Isso pode ser feito para avaliar quais grupos são diferentes de quais outros grupos ou para testar várias outras hipóteses focalizadas. Os testes de acompanhamento geralmente são diferenciados em termos de serem "planejados" (a priori) ou "post hoc." Testes planejados são determinados antes de olhar para os dados, e testes post hoc são concebidos somente depois de olhar para os dados (embora o termo "post hoc" seja usado de forma inconsistente).

Os testes de acompanhamento podem ser "simples" comparações pareadas de grupos individuais significam ou podem ser "compostas" comparações (por exemplo, comparando o agrupamento médio entre os grupos A, B e C com a média do grupo D). As comparações também podem observar testes de tendência, como relações lineares e quadráticas, quando a variável independente envolve níveis ordenados. Freqüentemente, os testes de acompanhamento incorporam um método de ajuste para o problema de comparações múltiplas.

Os testes de acompanhamento para identificar quais grupos, variáveis ou fatores específicos têm médias estatisticamente diferentes incluem o teste de intervalo de Tukey e o novo teste de intervalo múltiplo de Duncan. Por sua vez, esses testes geralmente são seguidos por uma metodologia de exibição de letras compactas (CLD) para tornar a saída dos testes mencionados mais transparentes para um público não estatístico.

Desenhos de estudo

Existem vários tipos de ANOVA. Muitos estatísticos baseiam a ANOVA no projeto do experimento, especialmente no protocolo que especifica a atribuição aleatória de tratamentos aos sujeitos; a descrição do protocolo do mecanismo de atribuição deve incluir uma especificação da estrutura dos tratamentos e de qualquer bloqueio. Também é comum aplicar ANOVA a dados observacionais usando um modelo estatístico apropriado.

Alguns designs populares usam os seguintes tipos de ANOVA:

• ANOVA unidirecional é usada para testar diferenças entre dois ou mais grupos independentes (média), por exemplo, diferentes níveis de aplicação ureia em uma safra, ou diferentes níveis de ação antibiótica em várias espécies bacterianas diferentes, ou diferentes níveis de efeito de algum medicamento em grupos de pacientes. No entanto, estes grupos não devem ser independentes, e há uma ordem nos grupos (como doença leve, moderada e grave), ou na dose de uma droga (como 5 mg/mL, 10 mg/mL, 20 mg/mL) dada ao mesmo grupo de pacientes, então uma estimativa de tendência linear deve ser usada. Tipicamente, no entanto, o ANOVA unidirecional é usado para testar diferenças entre pelo menos três grupos, uma vez que o caso de dois grupos pode ser coberto por um teste t. Quando há apenas dois meios para comparar, o teste t e o teste F ANOVA são equivalentes; a relação entre ANOVA e ANOVA ) é dado por F = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = )².
• O ANOVA Fatorial é usado quando há mais de um fator.
• Medidas repetidas ANOVA é usado quando os mesmos sujeitos são usados para cada fator (por exemplo, em um estudo longitudinal).
• A análise multivariada de variância (MANOVA) é usada quando há mais de uma variável de resposta.

Cuidados

Experimentos balanceados (aqueles com um tamanho de amostra igual para cada tratamento) são relativamente fáceis de interpretar; experimentos desbalanceados oferecem mais complexidade. Para ANOVA de fator único (one-way), o ajuste para dados não balanceados é fácil, mas a análise não balanceada carece de robustez e poder. Para projetos mais complexos, a falta de equilíbrio leva a mais complicações. "A propriedade de ortogonalidade dos principais efeitos e interações presentes em dados balanceados não é transferida para o caso desbalanceado. Isso significa que as técnicas usuais de análise de variância não se aplicam. Conseqüentemente, a análise de fatoriais desbalanceados é muito mais difícil do que para experimentos balanceados." No caso geral, "A análise de variância também pode ser aplicada a dados não balanceados, mas então as somas dos quadrados, quadrados médios e F-ratios dependerão da ordem em que os fontes de variação são consideradas."

ANOVA é (em parte) um teste de significância estatística. A American Psychological Association (e muitas outras organizações) sustenta a visão de que simplesmente relatar a significância estatística é insuficiente e que relatar limites de confiança é preferível.

Generalizações

ANOVA é considerada um caso especial de regressão linear que, por sua vez, é um caso especial do modelo linear geral. Todos consideram as observações como a soma de um modelo (ajuste) e um resíduo (erro) a ser minimizado.

O teste de Kruskal-Wallis e o teste de Friedman são testes não paramétricos, que não dependem de uma suposição de normalidade.

Conexão com regressão linear

Abaixo, deixamos clara a conexão entre ANOVA multiway e regressão linear.

Reordenar linearmente os dados para que kNão.-a observação está associada a uma resposta Sim.k{\displaystyle y_{k}} e fatores Z.k,b)Não. Z_{k,b}} Onde? b)∈ ∈ (1,2,... ... ,B?{\displaystyle b\in \{1,2,\ldots B\}} denota os diferentes fatores e BNão. é o número total de fatores. Em um sentido ANOVA B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Não. e em duas vias ANOVA B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2- Sim.. Além disso, assumimos o b)Não.-o fator tem Eu...b)Não. I_{b}} níveis, nomeadamente (1,2,... ... ,Eu...b)?{\displaystyle \{1,2,\ldotsI_{b}\}}. Agora, podemos codificar um tiro os fatores no Gerenciamento Gerenciamento b)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1BEu...b)- Sim. _{b=1}^{B}I_{b}} vetor dimensional vkNão. v_{k}}.

A função de codificação de um tiro gb):(1,2,... ... ,Eu...b)?↦ ↦ (0,1?Eu...b)Não. g_{b}:\{1,2,\ldotsI_{b}\}\mapsto \{0,1\}^{I_{b}}} é definido tal que o Eu...Não.-a entrada de gb)(Z.k,b))(Z_{k,b})} o

gb)(Z.k,b))Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(1seEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Z.k,b)0caso contrário{\displaystyle g_{b}(Z_{k,b})_{i}={\begin{cases}1&{\text{if }}i=Z_{k,b}\\0&{\text{otherwise}}\end{cases}}}

vkNão. v_{k}}

b)Não.

vk= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.g1(Z.k,1),g2(Z.k,2),... ... ,gB(Z.k,B)]Não. v_{k}=[g_{1}(Z_{k,1}),g_{2}(Z_{k,2}),\ldotsg_{B}(Z_{k,B})}]}

BNão.

vkNão. v_{k}}

XkNão. X_{k}}

Com esta notação no lugar, agora temos a conexão exata com a regressão linear. Nós simplesmente regressamos resposta Sim.k{\displaystyle y_{k}} contra o vetor XkNão. X_{k}}. No entanto, há uma preocupação com a identidade. Para superar essas questões, presumimos que a soma dos parâmetros dentro de cada conjunto de interações é igual a zero. A partir daqui, pode-se usar F-estatística ou outros métodos para determinar a relevância dos fatores individuais.

Exemplo

Podemos considerar o exemplo de interação bidirecional onde assumimos que o primeiro fator tem 2 níveis e o segundo fator tem 3 níveis.

Definir umEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Não. Arrombado se Z.k,1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...Não. Z_{k,1}=i} e b)Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Não. B_{i}=1} se Z.k,2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...Não. Z_{k,2}=i}, i.e. umNão. é a codificação one-hot do primeiro fator e b)Não. é a codificação one-hot do segundo fator.

Com isso,

Xk= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.um1,um2,b)1,b)2,b)3,um1× × b)1,um1× × b)2,um1× × b)3,um2× × b)1,um2× × b)2,um2× × b)3,1]Não. X_{k}=[a_{1},a_{2},b_{1},b_{2},b_{3},a_{1}\times b_{1},a_{1}\times b_{2},a_{1}\times b_{3},a_{2}\times b_{1},a_{2}\times b_{2},a_{2}\times b_{3},1]}

Z.k,1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2Z.k,2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1{\displaystyle {\begin{aligned}Z_{k,1}&=2\Z_{k,2}&=1\end{aligned}}}

Xk= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.0,1,1,0,0,0,0,0,1,0,0,1]Não. X_{k}=[0,1,0,0,0,0,0,0,0,0,0,1]}