Algoritmo de pesquisa binária

AjustarCompartirImprimirCitar

Procurar algoritmo encontrar a posição de um valor de destino dentro de um array classificado

Na ciência da computação, pesquisa binária, também conhecida como pesquisa de meio intervalo, pesquisa logarítmica ou corte binário, é um algoritmo de busca que encontra a posição de um valor de destino dentro de uma matriz classificada. A pesquisa binária compara o valor de destino com o elemento do meio da matriz. Se não forem iguais, a metade em que o alvo não pode estar é eliminada e a busca continua na metade restante, novamente tomando o elemento do meio para comparar com o valor alvo, e repetindo isso até que o valor alvo seja encontrado. Se a pesquisa terminar com a metade restante vazia, o alvo não está na matriz.

Pesquisa binária é executada em tempo logarítmico no pior caso, fazendo $O(log n)$ comparações, onde $n$ é o número de elementos no array. A busca binária é mais rápida do que a busca linear, exceto para pequenos arrays. No entanto, o array deve ser classificado primeiro para ser capaz de aplicar a pesquisa binária. Existem estruturas de dados especializadas projetadas para pesquisa rápida, como tabelas hash, que podem ser pesquisadas de forma mais eficiente do que a busca binária. No entanto, a busca binária pode ser usada para resolver uma ampla gama de problemas, como encontrar o elemento mais próximo ou mais grande no array em relação ao alvo, mesmo que esteja ausente do array.

Existem inúmeras variações de pesquisa binária. Em particular, a cascata fracionária acelera as pesquisas binárias para o mesmo valor em várias matrizes. A cascata fracionária resolve com eficiência vários problemas de pesquisa em geometria computacional e em vários outros campos. A pesquisa exponencial estende a pesquisa binária para listas ilimitadas. A árvore de pesquisa binária e as estruturas de dados da árvore B são baseadas na pesquisa binária.

Algoritmo

A pesquisa binária funciona em arrays classificados. A pesquisa binária começa comparando um elemento no meio da matriz com o valor de destino. Se o valor de destino corresponder ao elemento, sua posição na matriz será retornada. Se o valor de destino for menor que o elemento, a pesquisa continua na metade inferior da matriz. Se o valor de destino for maior que o elemento, a pesquisa continua na metade superior da matriz. Ao fazer isso, o algoritmo elimina a metade em que o valor alvo não pode estar em cada iteração.

Procedimento

Dado um array $A$ de $n$ elementos com valores ou registros ${displaystyle A_{0},A_{1},A_{2},ldotsA_{n-1}}$ resolver tal que ${displaystyle A_{0}leq A_{1}leq A_{2}leq cdots leq A_{n-1}}$ , e valor alvo $T$ , a subrotina seguinte usa a pesquisa binária para encontrar o índice de $T$ em $A$ .

Conjunto $L$ para $0$ e $R$ para $n-1$ .
Se $R}" xmlns="http://www.w3.org/1998/Math/MathML">L>R- Sim. R}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/145ce1d631364a50d19ac5264c7dc09d4e158b0a" style="vertical-align: -0.338ex; width:6.445ex; height:2.176ex;"/>$ , a busca termina como mal sucedida.
Conjunto $m$ (a posição do elemento médio) para o chão de ${displaystyle {frac {L+R}{2}}}$ , que é o maior inteiro menos ou igual a ${displaystyle {frac {L+R}{2}}}$ .
Se $<math alttext="{displaystyle A_{m}Am<TNão. A_{m}<T}<img alt="{displaystyle A_{m}$ , set $L$ para $m+1$ e ir para o passo 2.
Se $T}" xmlns="http://www.w3.org/1998/Math/MathML">Am>TNão. A_{m}> T.T}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d8f333a047adf793929566dda96ffdf4493cf3b7" style="vertical-align: -0.671ex; width:8.153ex; height:2.509ex;"/>$ , set $R$ para $m-1$ e ir para o passo 2.
Agora! ${displaystyle A_{m}=T}$ , a busca é feita; retornar $m$ .

Este procedimento iterativo mantém o controle dos limites de pesquisa com as duas variáveis $L$ e $R$ . O procedimento pode ser expresso em pseudocódigo da seguinte forma, quando os nomes e tipos variáveis permanecem os mesmos que acima, floor é a função do chão, e unsuccessful refere-se a um valor específico que transmite a falha da pesquisa.

pesquisa binária

função binário_search(A, n, T) oEu... 0
R:= n − 1
 enquanto L ≤ R dom: = chão (L + R) / 2)
 se A[m] < T entãoL: = m + 1
 se A[m] > T entãoR:= m − 1
 mais:
 retorno m
 retorno sem sucesso

Alternativamente, o algoritmo pode tomar o teto de ${displaystyle {frac {L+R}{2}}}$ . Isso pode alterar o resultado se o valor de destino aparecer mais de uma vez no array.

Procedimento alternativo

No procedimento acima, o algoritmo verifica se o elemento médio ( $m$ ) é igual ao alvo ( $T$ ) em cada iteração. Algumas implementações deixam de fora esta verificação durante cada iteração. O algoritmo realizaria esta verificação somente quando um elemento é deixado (quando ${displaystyle L=R}$ ). Isso resulta em um loop de comparação mais rápido, pois uma comparação é eliminada por iteração, enquanto requer apenas mais uma iteração em média.

Hermann Bottenbruch publicou a primeira implementação para deixar de fora esta verificação em 1962.

Conjunto $L$ para $0$ e $R$ para $n-1$ .
Enquanto L≠ ≠ RNão. Lneq R} ${displaystyle Lneq R}$ ,
1. Conjunto $m$ (a posição do elemento médio) para o teto de ${displaystyle {frac {L+R}{2}}}$ , que é o menos inteiro maior ou igual a ${displaystyle {frac {L+R}{2}}}$ .
2. Se $T}" xmlns="http://www.w3.org/1998/Math/MathML">Am>TNão. A_{m}> T.T}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d8f333a047adf793929566dda96ffdf4493cf3b7" style="vertical-align: -0.671ex; width:8.153ex; height:2.509ex;"/>$ , set $R$ para $m-1$ .
3. Else, ${displaystyle A_{m}leq T}$ ; conjunto $L$ para $m$ .
Agora! ${displaystyle L=R}$ , a busca é feita. Se ${displaystyle A_{L}=T}$ , retorno $L$ . Caso contrário, a busca termina como mal sucedida.

Onde ceil é a função de teto, o pseudocódigo para esta versão é:

função binário_search_alternative(A, n, T) oEu... 0
R:= n − 1
 enquanto L! R dom:= ceil(L + R) / 2)
 se A[m] > T entãoR:= m − 1
 mais:
Eu... m
 se A[L] = T então retorno L
 retorno sem sucesso

Duplicar elementos

O procedimento pode retornar qualquer índice cujo elemento é igual ao valor alvo, mesmo que haja elementos duplicados no array. Por exemplo, se o array a ser pesquisado foi ${displaystyle [1,2,3,4,4,5,6,7]}$ e o alvo foi $4$ , então seria correto para o algoritmo retornar o 4o (index 3) ou 5o (index 4) elemento. O procedimento regular retornaria o 4o elemento (index 3) neste caso. Ele nem sempre retorna a primeira duplicata (considere ${displaystyle [1,2,4,4,4,5,6,7]}$ que ainda retorna o 4o elemento). No entanto, às vezes é necessário encontrar o elemento mais esquerdo ou o elemento mais certo para um valor de destino que é duplicado no array. No exemplo acima, o 4o elemento é o elemento mais esquerdo do valor 4, enquanto o 5o elemento é o elemento mais direito do valor 4. O procedimento alternativo acima sempre retornará o índice do elemento mais certo se tal elemento existir.

Procedimento para encontrar o elemento mais à esquerda

Para encontrar o elemento mais à esquerda, o seguinte procedimento pode ser usado:

Conjunto $L$ para $0$ e $R$ para $n$ .
Enquanto <math alttext="{displaystyle LL<RNão. L<R<img alt="{displaystyle L,
1. Conjunto $m$ (a posição do elemento médio) para o chão de ${displaystyle {frac {L+R}{2}}}$ , que é o maior inteiro menos ou igual a ${displaystyle {frac {L+R}{2}}}$ .
2. Se $<math alttext="{displaystyle A_{m}Am<TNão. A_{m}<T}<img alt="{displaystyle A_{m}$ , set $L$ para $m+1$ .
3. Else, ${displaystyle A_{m}geq T}$ ; conjunto $R$ para $m$ .
Voltar $L$ .

Se $<math alttext="{displaystyle LL<nNão. L<n. <img alt="{displaystyle L$ e ${displaystyle A_{L}=T}$ , então $A_{L}$ é o elemento mais esquerdo que é igual $T$ . Mesmo que $T$ não está no array, $L$ é a classificação $T$ no array, ou o número de elementos no array que são menos do que $T$ .

Onde floor é a função floor, o pseudocódigo para esta versão é:

função binário_search_leftmost(A, n, T):
Eu... 0
R... n
 enquanto L < R:
m: = chão (L + R) / 2)
 se A[m] < T:
L: = m + 1
 mais:
R... m
 retorno L

Procedimento para encontrar o elemento mais à direita

Para encontrar o elemento mais à direita, o seguinte procedimento pode ser usado:

Conjunto $L$ para $0$ e $R$ para $n$ .
Enquanto <math alttext="{displaystyle LL<RNão. L<R<img alt="{displaystyle L,
1. Conjunto $m$ (a posição do elemento médio) para o chão de ${displaystyle {frac {L+R}{2}}}$ , que é o maior inteiro menos ou igual a ${displaystyle {frac {L+R}{2}}}$ .
2. Se $T}" xmlns="http://www.w3.org/1998/Math/MathML">Am>TNão. A_{m}> T.T}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d8f333a047adf793929566dda96ffdf4493cf3b7" style="vertical-align: -0.671ex; width:8.153ex; height:2.509ex;"/>$ , set $R$ para $m$ .
3. Else, ${displaystyle A_{m}leq T}$ ; conjunto $L$ para $m+1$ .
Voltar ${displaystyle R-1}$ .

Se $0}" xmlns="http://www.w3.org/1998/Math/MathML">R>0- Sim. 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/57914127d03a5cea02c60a32cfbb22f34904f00d" style="vertical-align: -0.338ex; width:6.025ex; height:2.176ex;"/>$ e ${displaystyle A_{R-1}=T}$ , então ${displaystyle A_{R-1}}$ é o elemento mais certo que é igual $T$ . Mesmo que $T$ não está no array, ${displaystyle n-R}$ é o número de elementos no array que são maiores do que $T$ .

Onde floor é a função floor, o pseudocódigo para esta versão é:

função binário_search_rightmost(A, n, T):
Eu... 0
R... n
 enquanto L < R:
m: = chão (L + R) / 2)
 se A[m] > T:
R... m
 mais:
L: = m + 1
 retorno R - 1

Correspondências aproximadas

A busca binária pode ser adaptada para calcular partidas aproximadas. No exemplo acima, o posto, antecessor, sucessor e vizinho mais próximo são mostrados para o valor alvo

5

, que não está no array.

O procedimento acima executa apenas correspondências exatas, encontrando a posição de um valor alvo. No entanto, é trivial estender a pesquisa binária para realizar correspondências aproximadas porque a pesquisa binária opera em matrizes classificadas. Por exemplo, a pesquisa binária pode ser usada para calcular, para um determinado valor, sua classificação (o número de elementos menores), predecessor (próximo menor elemento), sucessor (próximo elemento maior) e vizinho mais próximo. As consultas de intervalo que buscam o número de elementos entre dois valores podem ser realizadas com duas consultas de classificação.

Consultas aleatórias podem ser realizadas com o procedimento para encontrar o elemento mais esquerdo. O número de elementos menos do que o valor alvo é retornado pelo procedimento.
Consultas do predecessor podem ser realizadas com consultas de classificação. Se a classificação do valor alvo for $r$ , seu antecessor é $r-1$ .
Para consultas de sucessor, o procedimento para encontrar o elemento mais correto pode ser usado. Se o resultado da execução do procedimento para o valor alvo for $r$ , então o sucessor do valor alvo é $r+1$ .
O vizinho mais próximo do valor-alvo é seu antecessor ou sucessor, o que quer que seja mais próximo.
As consultas de intervalo também são simples. Uma vez que as fileiras dos dois valores são conhecidos, o número de elementos maiores ou iguais ao primeiro valor e menos do que o segundo é a diferença das duas fileiras. Esta contagem pode ser ajustada até ou para baixo por um de acordo com se os pontos finais do intervalo devem ser considerados como parte do intervalo e se o array contém entradas correspondentes aos pontos finais.

Desempenho

Uma árvore que representa a busca binária. O array que está sendo pesquisado aqui é

{displaystyle [20,30,40,50,80,90,100]}

, e o valor alvo é

{displaystyle 40}

O pior caso é alcançado quando a pesquisa atinge o nível mais profundo da árvore, enquanto o melhor caso é alcançado quando o valor alvo é o elemento médio.

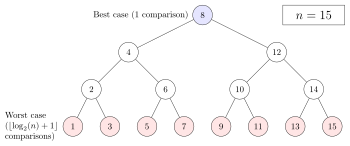
Em termos de número de comparações, o desempenho da pesquisa binária pode ser analisado visualizando a execução do procedimento em uma árvore binária. O nó raiz da árvore é o elemento do meio da matriz. O elemento do meio da metade inferior é o nó filho esquerdo da raiz e o elemento do meio da metade superior é o nó filho direito da raiz. O restante da árvore é construído de maneira semelhante. A partir do nó raiz, as subárvores esquerda ou direita são percorridas, dependendo se o valor de destino é menor ou maior que o nó em consideração.

No pior dos casos, a busca binária faz ${textstyle lfloor log _{2}(n)+1rfloor }$ iterações do loop de comparação, onde o ${textstyle lfloor rfloor }$ notação denota a função de chão que produz o maior inteiro menos ou igual ao argumento, e ${textstyle log _{2}}$ é o logaritmo binário. Isso porque o pior caso é alcançado quando a busca atinge o nível mais profundo da árvore, e há sempre ${textstyle lfloor log _{2}(n)+1rfloor }$ níveis na árvore para qualquer busca binária.

O pior caso também pode ser alcançado quando o elemento alvo não está no array. Se ${textstyle n}$ é um menos do que um poder de dois, então este é sempre o caso. Caso contrário, a pesquisa pode executar ${textstyle lfloor log _{2}(n)+1rfloor }$ iterações se a busca atingir o nível mais profundo da árvore. No entanto, pode fazer ${textstyle lfloor log _{2}(n)rfloor }$ iterações, que é um menos do que o pior caso, se a pesquisa termina no segundo nível mais profundo da árvore.

Em média, assumindo que cada elemento é igualmente provável que seja pesquisado, a busca binária faz ${displaystyle lfloor log _{2}(n)rfloor +1-(2^{lfloor log _{2}(n)rfloor +1}-lfloor log _{2}(n)rfloor -2)/n}$ iterações quando o elemento alvo está no array. Isto é aproximadamente igual a ${displaystyle log _{2}(n)-1}$ iterações. Quando o elemento alvo não está no array, a busca binária faz ${displaystyle lfloor log _{2}(n)rfloor +2-2^{lfloor log _{2}(n)rfloor +1}/(n+1)}$ as iterações em média, supondo que o intervalo entre e elementos externos é igualmente susceptível de ser pesquisado.

No melhor caso, onde o valor de destino é o elemento do meio da matriz, sua posição é retornada após uma iteração.

Em termos de iterações, nenhum algoritmo de busca que funcione apenas comparando elementos pode exibir melhor desempenho médio e de pior caso do que a busca binária. A árvore de comparação que representa a pesquisa binária tem o menor número possível de níveis, pois todos os níveis acima do nível mais baixo da árvore são preenchidos completamente. Caso contrário, o algoritmo de busca pode eliminar poucos elementos em uma iteração, aumentando o número de iterações necessárias no caso médio e pior. Este é o caso de outros algoritmos de pesquisa baseados em comparações, pois, embora possam funcionar mais rapidamente em alguns valores de destino, o desempenho médio em todos os elementos é pior do que a pesquisa binária. Ao dividir a matriz ao meio, a pesquisa binária garante que o tamanho de ambas as submatrizes seja o mais semelhante possível.

Complexidade espacial

Pesquisa binária requer três ponteiros para elementos, que podem ser índices de matriz ou ponteiros para locais de memória, independentemente do tamanho do array. Portanto, a complexidade do espaço da pesquisa binária é $O(1)$ na palavra RAM modelo de computação.

Derivação do caso médio

O número médio de iterações realizadas pela pesquisa binária depende da probabilidade de cada elemento ser pesquisado. O caso médio é diferente para pesquisas bem sucedidas e pesquisas mal sucedidas. Presume-se que cada elemento é igualmente provável ser pesquisado para pesquisas bem sucedidas. Para pesquisas mal sucedidas, será assumido que os intervalos entre e elementos externos são igualmente susceptíveis de ser pesquisados. O caso médio para pesquisas bem sucedidas é o número de iterações necessárias para pesquisar cada elemento exatamente uma vez, dividido por $n$ , o número de elementos. O caso médio para pesquisas mal sucedidas é o número de iterações necessárias para procurar um elemento dentro de cada intervalo exatamente uma vez, dividido pelo $n+1$ intervalos.

Pesquisas bem-sucedidas

Na representação da árvore binária, uma busca bem sucedida pode ser representada por um caminho da raiz para o nó alvo, chamado de caminho interno. O comprimento de um caminho é o número de bordas (conexões entre nós) que o caminho passa. O número de iterações realizadas por uma pesquisa, dado que o caminho correspondente tem comprimento $l$ , ${displaystyle l+1}$ contando a iteração inicial. O comprimento do caminho interno é a soma dos comprimentos de todos os caminhos internos únicos. Uma vez que há apenas um caminho da raiz para qualquer nó único, cada caminho interno representa uma busca por um elemento específico. Se houver $n$ elementos, que é um inteiro positivo, e o comprimento do caminho interno é $I(n)$ , então o número médio de iterações para uma pesquisa bem sucedida ${displaystyle T(n)=1+{frac {I(n)}{n}}}$ , com a única iteração adicionada para contar a iteração inicial.

Uma vez que a pesquisa binária é o algoritmo ideal para pesquisar com comparações, este problema é reduzido para calcular o comprimento mínimo do caminho interno de todas as árvores binárias com $n$ nós, que é igual a:

${displaystyle I(n)=sum _{k=1}^{n}leftlfloor log _{2}(k)rightrfloor }$

Por exemplo, em uma matriz de 7 elementos, a raiz requer uma iteração, os dois elementos abaixo da raiz requerem duas iterações e os quatro elementos abaixo requerem três iterações. Neste caso, o comprimento do caminho interno é:

${displaystyle sum _{k=1}^{7}leftlfloor log _{2}(k)rightrfloor =0+2(1)+4(2)=2+8=10}$

O número médio de iterações seria ${displaystyle 1+{frac {10}{7}}=2{frac {3}{7}}}$ baseado na equação para o caso médio. A soma para $I(n)$ pode ser simplificado para:

${displaystyle I(n)=sum _{k=1}^{n}leftlfloor log _{2}(k)rightrfloor =(n+1)leftlfloor log _{2}(n+1)rightrfloor -2^{leftlfloor log _{2}(n+1)rightrfloor +1}+2}$

Substituir a equação para $I(n)$ na equação para $T(n)$ :

${displaystyle T(n)=1+{frac {(n+1)leftlfloor log _{2}(n+1)rightrfloor -2^{leftlfloor log _{2}(n+1)rightrfloor +1}+2}{n}}=lfloor log _{2}(n)rfloor +1-(2^{lfloor log _{2}(n)rfloor +1}-lfloor log _{2}(n)rfloor -2)/n}$

Por inteiro $n$ , isto é equivalente à equação para o caso médio em uma pesquisa bem sucedida especificada acima.

Pesquisas malsucedidas

Pesquisas incertas podem ser representadas pelo aumento da árvore com nós, que forma um árvore binária estendida. Se um nó interno, ou um nó presente na árvore, tem menos de dois nós de criança, então nós de criança adicionais, chamados nós externos, são adicionados para que cada nó interno tenha duas crianças. Ao fazê-lo, uma busca mal sucedida pode ser representada como um caminho para um nó externo, cujo pai é o único elemento que permanece durante a última iteração. Um caminho externo é um caminho da raiz para um nó externo. O comprimento do caminho externo é a soma dos comprimentos de todos os caminhos externos únicos. Se houver $n$ elementos, que é um inteiro positivo, e o comprimento do caminho externo é $E(n)$ , então o número médio de iterações para uma busca mal sucedida ${displaystyle T'(n)={frac {E(n)}{n+1}}}$ , com a única iteração adicionada para contar a iteração inicial. O comprimento do caminho externo é dividido por $n+1$ em vez de $n$ porque há $n+1$ caminhos externos, representando os intervalos entre e fora os elementos do array.

Este problema pode igualmente ser reduzido para determinar o comprimento mínimo do caminho externo de todas as árvores binárias com $n$ nós. Para todas as árvores binárias, o comprimento do caminho externo é igual ao comprimento do caminho interno mais $2n$ . Substituir a equação para $I(n)$ :

${displaystyle E(n)=I(n)+2n=left[(n+1)leftlfloor log _{2}(n+1)rightrfloor -2^{leftlfloor log _{2}(n+1)rightrfloor +1}+2right]+2n=(n+1)(lfloor log _{2}(n)rfloor +2)-2^{lfloor log _{2}(n)rfloor +1}}$

Substituir a equação para $E(n)$ na equação para ${displaystyle T'(n)}$ , o caso médio para pesquisas malsucedidas pode ser determinado:

${displaystyle T'(n)={frac {(n+1)(lfloor log _{2}(n)rfloor +2)-2^{lfloor log _{2}(n)rfloor +1}}{(n+1)}}=lfloor log _{2}(n)rfloor +2-2^{lfloor log _{2}(n)rfloor +1}/(n+1)}$

Execução de procedimento alternativo

Cada iteração do procedimento de pesquisa binária definido acima faz uma ou duas comparações, verificando se o elemento médio é igual ao alvo em cada iteração. Assumindo que cada elemento é igualmente provável ser pesquisado, cada iteração faz 1,5 comparações em média. Uma variação do algoritmo verifica se o elemento médio é igual ao alvo no final da pesquisa. Em média, isso elimina metade de uma comparação de cada iteração. Isso reduz ligeiramente o tempo tomado por iteração na maioria dos computadores. No entanto, garante que a pesquisa leva o número máximo de iterações, em média adicionando uma iteração à pesquisa. Porque o loop de comparação é executado apenas ${textstyle lfloor log _{2}(n)+1rfloor }$ vezes no pior caso, o ligeiro aumento da eficiência por iteração não compensa a extra iteração para todos, mas muito grande ${textstyle n}$ .

Tempo de execução e uso de cache

Ao analisar o desempenho da pesquisa binária, outra consideração é o tempo necessário para comparar dois elementos. Para números inteiros e strings, o tempo necessário aumenta linearmente conforme o comprimento da codificação (geralmente o número de bits) dos elementos aumenta. Por exemplo, comparar um par de inteiros sem sinal de 64 bits exigiria a comparação de até o dobro dos bits ao comparar um par de inteiros sem sinal de 32 bits. O pior caso é alcançado quando os números inteiros são iguais. Isso pode ser significativo quando os comprimentos de codificação dos elementos são grandes, como com tipos inteiros grandes ou strings longas, o que torna a comparação de elementos dispendiosa. Além disso, comparar valores de ponto flutuante (a representação digital mais comum de números reais) geralmente é mais caro do que comparar números inteiros ou strings curtas.

Na maioria das arquiteturas de computador, o processador possui um cache de hardware separado da RAM. Como estão localizados dentro do próprio processador, os caches são muito mais rápidos de acessar, mas geralmente armazenam muito menos dados do que a RAM. Portanto, a maioria dos processadores armazena locais de memória que foram acessados recentemente, juntamente com locais de memória próximos a eles. Por exemplo, quando um elemento da matriz é acessado, o próprio elemento pode ser armazenado junto com os elementos que estão armazenados próximos a ele na RAM, tornando mais rápido o acesso sequencial aos elementos da matriz que estão próximos no índice uns dos outros (localidade de referência). Em uma matriz classificada, a pesquisa binária pode pular para locais de memória distantes se a matriz for grande, ao contrário dos algoritmos (como pesquisa linear e sondagem linear em tabelas de hash) que acessam elementos em sequência. Isso aumenta um pouco o tempo de execução da pesquisa binária para grandes matrizes na maioria dos sistemas.

Pesquisa binária versus outros esquemas

Os arrays classificados com pesquisa binária são uma solução muito ineficiente quando as operações de inserção e exclusão são intercaladas com recuperação, tomando ${textstyle O(n)}$ tempo para cada operação. Além disso, arrays classificados podem complicar o uso da memória especialmente quando os elementos são frequentemente inseridos no array. Existem outras estruturas de dados que suportam a inserção e exclusão muito mais eficientes. A pesquisa binária pode ser usada para executar a correspondência exata e definir a associação (determinando se um valor de destino está em uma coleção de valores). Existem estruturas de dados que suportam a correspondência exata mais rápida e definem a adesão. No entanto, ao contrário de muitos outros esquemas de pesquisa, a pesquisa binária pode ser usada para correspondência aproximada eficiente, geralmente executando tais jogos em ${textstyle O(log n)}$ tempo independentemente do tipo ou estrutura dos próprios valores. Além disso, existem algumas operações, como encontrar o menor e maior elemento, que pode ser executado de forma eficiente em um array classificado.

Pesquisa linear

Pesquisa linear é um algoritmo de pesquisa simples que verifica todos os registros até encontrar o valor de destino. Pesquisa linear pode ser feita em uma lista vinculada, que permite uma inserção e exclusão mais rápidas do que um array. A pesquisa binária é mais rápida do que a busca linear de arrays classificados, exceto se o array é curto, embora o array precise ser classificado de antemão. Todos os algoritmos de classificação baseados em elementos de comparação, como o quicksort e o merge sort, exigem pelo menos ${textstyle O(nlog n)}$ comparações no pior caso. Ao contrário da pesquisa linear, a pesquisa binária pode ser usada para correspondência aproximada eficiente. Existem operações como encontrar o menor e maior elemento que pode ser feito de forma eficiente em um array classificado, mas não em um array não ousado.

Árvores

As árvores de busca binárias são pesquisadas usando um algoritmo semelhante à pesquisa binária.

Uma árvore de pesquisa binária é uma estrutura de dados de árvore binária que funciona com base no princípio da pesquisa binária. Os registros da árvore são organizados em ordem de classificação e cada registro na árvore pode ser pesquisado usando um algoritmo semelhante à pesquisa binária, levando em média o tempo logarítmico. Inserção e exclusão também requerem tempo logarítmico médio em árvores de busca binária. Isso pode ser mais rápido do que a inserção e exclusão de tempo linear de matrizes classificadas, e as árvores binárias retêm a capacidade de executar todas as operações possíveis em uma matriz classificada, incluindo intervalos e consultas aproximadas.

No entanto, a busca binária é geralmente mais eficiente para pesquisar como árvores de busca binárias provavelmente será imperfeitamente equilibrada, resultando em um desempenho ligeiramente pior do que a busca binária. Isso mesmo se aplica a árvores de busca binárias equilibradas, árvores de busca binárias que equilibram seus próprios nós, porque raramente produzem a árvore com os mais poucos níveis possíveis. Exceto para árvores de busca binárias equilibradas, a árvore pode ser severamente desequilibrada com poucos nós internos com duas crianças, resultando no tempo de pesquisa médio e pior caso se aproximando ${textstyle n}$ comparações. As árvores de busca binárias ocupam mais espaço do que arrays ordenados.

Árvores de busca binária se prestam a buscas rápidas em memória externa armazenada em discos rígidos, já que árvores de busca binária podem ser estruturadas de forma eficiente em sistemas de arquivos. A árvore B generaliza esse método de organização da árvore. As árvores B são freqüentemente usadas para organizar o armazenamento de longo prazo, como bancos de dados e sistemas de arquivos.

Hashing

Para implementar matrizes associativas, as tabelas hash, uma estrutura de dados que mapeia chaves para registros usando uma função hash, geralmente são mais rápidas do que a pesquisa binária em uma matriz classificada de registros. A maioria das implementações de tabela hash requer apenas tempo constante amortizado em média. No entanto, o hash não é útil para correspondências aproximadas, como calcular a próxima menor, a próxima maior e a chave mais próxima, pois a única informação fornecida em uma pesquisa com falha é que o destino não está presente em nenhum registro. A busca binária é ideal para tais correspondências, realizando-as em tempo logarítmico. A pesquisa binária também suporta correspondências aproximadas. Algumas operações, como encontrar o menor e o maior elemento, podem ser feitas com eficiência em arrays classificados, mas não em tabelas de hash.

Definir algoritmos de associação

Um problema relacionado à pesquisa é a associação definida. Qualquer algoritmo que faça pesquisa binária, como pesquisa binária, também pode ser usado para a associação definida. Existem outros algoritmos que são mais especificamente adequados para a associação definida. Um array de bits é o mais simples, útil quando o intervalo de chaves é limitado. Ele armazena compactamente uma coleção de bits, com cada bit representando uma única chave dentro da gama de chaves. Alguns arrays são muito rápidos, exigindo apenas ${textstyle O(1)}$ Hora. O tipo Judy1 do array Judy lida com chaves de 64 bits de forma eficiente.

Para resultados aproximados, os filtros Bloom, outra estrutura de dados probabilística baseada em hashing, armazenam um conjunto de chaves codificando as chaves usando um array de bits e várias funções hash. Os filtros Bloom são muito mais eficientes no espaço do que os arrays de bits na maioria dos casos e não muito mais lentos: com ${textstyle k}$ funções hash, consultas de associação exigem apenas ${textstyle O(k)}$ Hora. No entanto, os filtros Bloom sofrem de falsos positivos.

Outras estruturas de dados

Existem estruturas de dados que podem melhorar a pesquisa binária em alguns casos, tanto para pesquisa quanto para outras operações disponíveis para arrays classificados. Por exemplo, pesquisas, correspondências aproximadas e as operações disponíveis para arrays classificados podem ser executadas com mais eficiência do que a pesquisa binária em estruturas de dados especializadas, como árvores van Emde Boas, árvores de fusão, tentativas e arrays de bits. Essas estruturas de dados especializadas geralmente são mais rápidas porque aproveitam as propriedades das chaves com um determinado atributo (geralmente chaves que são números inteiros pequenos) e, portanto, consumirão tempo ou espaço para chaves que não possuem esse atributo. Contanto que as chaves possam ser ordenadas, essas operações sempre podem ser feitas pelo menos com eficiência em uma matriz classificada, independentemente das chaves. Algumas estruturas, como Judy arrays, usam uma combinação de abordagens para mitigar isso, mantendo a eficiência e a capacidade de realizar correspondência aproximada.

Variações

Pesquisa binária uniforme

A busca binária uniforme armazena a diferença entre a corrente e os dois próximos elementos médios possíveis em vez de limites específicos.

Lojas de pesquisa binárias uniformes, em vez dos limites inferiores e superiores, a diferença no índice do elemento médio da iteração atual para a próxima iteração. Uma tabela de pesquisa contendo as diferenças é computada de antemão. Por exemplo, se o array a ser pesquisado é $[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]$ , o elemento central ( $m$ ) seria $6$ . Neste caso, o elemento central do subarray esquerdo ( $[1, 2, 3, 4, 5]$ ) $3$ e o elemento médio do subarray direito ( $[7, 8, 9, 10, 11]$ ) $9$ . Busca binária uniforme armazenaria o valor de $3$ como ambos os índices diferem de $6$ por esta mesma quantidade. Para reduzir o espaço de pesquisa, o algoritmo adiciona ou subtrai essa mudança do índice do elemento médio. A busca binária uniforme pode ser mais rápida em sistemas onde é ineficiente para calcular o ponto médio, como em computadores decimais.

Pesquisa exponencial

Visualização de busca exponencial encontrando o limite superior para a pesquisa binária subsequente

A busca experimental estende a pesquisa binária a listas não distribuídas. Começa por encontrar o primeiro elemento com um índice que é tanto um poder de dois quanto maior do que o valor alvo. Depois, ele define esse índice como o limite superior, e muda para a pesquisa binária. Uma busca leva ${textstyle lfloor log _{2}x+1rfloor }$ iterações antes da pesquisa binária é iniciada e no máximo ${textstyle lfloor log _{2}xrfloor }$ iterações da pesquisa binária, onde ${textstyle x}$ é a posição do valor alvo. A busca exonential funciona em listas limitadas, mas se torna uma melhoria na busca binária somente se o valor de destino estiver próximo ao início do array.

Pesquisa de interpolação

Visualização da pesquisa de interpolação usando interpolação linear. Neste caso, nenhuma pesquisa é necessária porque a estimativa da localização do alvo dentro do array está correta. Outras implementações podem especificar outra função para estimar a localização do alvo.

Em vez de calcular o ponto médio, a pesquisa de interpolação estima a posição do valor de destino, levando em consideração os elementos mais baixos e mais altos da matriz, bem como o comprimento da matriz. Funciona com base no fato de que o ponto médio não é o melhor palpite em muitos casos. Por exemplo, se o valor de destino estiver próximo ao elemento mais alto na matriz, é provável que esteja localizado próximo ao final da matriz.

Uma função de interpolação comum é a interpolação linear. Se $A$ é o array, ${displaystyle L,R}$ são os limites inferiores e superiores, respectivamente, e $T$ é o alvo, então o alvo é estimado para ser aproximadamente ${displaystyle (T-A_{L})/(A_{R}-A_{L})}$ do caminho entre $L$ e $R$ . Quando a interpolação linear é usada, e a distribuição dos elementos de matriz é uniforme ou quase uniforme, a pesquisa de interpolação faz ${textstyle O(log log n)}$ comparações.

Na prática, a pesquisa por interpolação é mais lenta do que a pesquisa binária para arrays pequenos, pois a pesquisa por interpolação requer computação extra. Sua complexidade de tempo cresce mais lentamente do que a pesquisa binária, mas isso apenas compensa a computação extra para matrizes grandes.

Cascata fracionária

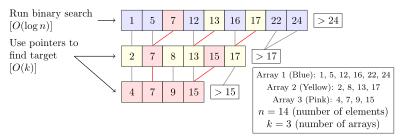
Em cascata fracional, cada array tem ponteiros para cada segundo elemento de outro array, então apenas uma busca binária tem de ser realizada para pesquisar todos os arrays.

A cascata fracional é uma técnica que acelera pesquisas binárias para o mesmo elemento em vários arrays classificados. Pesquisar cada array separadamente requer ${textstyle O(klog n)}$ hora, onde ${textstyle k}$ é o número de arrays. Em cascata fracionária reduz isto a ${textstyle O(k+log n)}$ armazenando informações específicas em cada array sobre cada elemento e sua posição nos outros arrays.

A cascata fracionária foi originalmente desenvolvida para resolver com eficiência vários problemas de geometria computacional. A cascata fracionária foi aplicada em outros lugares, como na mineração de dados e no roteamento de protocolo da Internet.

Generalização para gráficos

Pesquisa binária tem sido generalizada para trabalhar em certos tipos de gráficos, onde o valor de destino é armazenado em um vértice em vez de um elemento de matriz. As árvores de busca binárias são uma tal generalização – quando um vértice (nó) na árvore é sequentado, o algoritmo ou aprende que o vértice é o alvo, ou de outra forma que subárvore o alvo estaria localizado dentro. No entanto, isso pode ser mais generalizado como segue: dado um grafo não direcionado, ponderado positivamente e um vértice alvo, o algoritmo aprende ao consultar um vértice que é igual ao alvo, ou é dado uma borda incidente que está no caminho mais curto do vértice que secou para o alvo. O algoritmo de busca binário padrão é simplesmente o caso em que o gráfico é um caminho. Da mesma forma, as árvores de busca binárias são o caso em que as bordas para as subárvores esquerda ou direita são dadas quando o vértice queselado é desigual ao alvo. Para todos os gráficos não direcionados, positivamente ponderados, há um algoritmo que encontra o vértice alvo em $O(log n)$ consultas no pior caso.

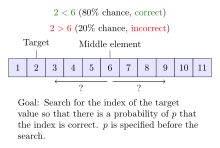
Pesquisa binária com ruído

Em busca binária ruidosa, há uma certa probabilidade de que uma comparação esteja incorreta.

Os algoritmos de busca binário ruidosos resolvem o caso em que o algoritmo não pode comparar de forma confiável elementos do array. Para cada par de elementos, há uma certa probabilidade de que o algoritmo faz a comparação errada. Pesquisa binária barulhenta pode encontrar a posição correta do alvo com uma determinada probabilidade que controla a confiabilidade da posição cedida. Cada procedimento de busca binário ruidoso deve fazer pelo menos ${displaystyle (1-tau){frac {log _{2}(n)}{H(p)}}-{frac {10}{H(p)}}}$ comparações em média, onde ${displaystyle H(p)=-plog _{2}(p)-(1-p)log _{2}(1-p)}$ é a função de entropia binária e $tau$ é a probabilidade de que o procedimento rende a posição errada. O problema de pesquisa binária barulhento pode ser considerado como um caso do jogo Rényi-Ulam, uma variante de Vinte Perguntas onde as respostas podem estar erradas.

Pesquisa binária quântica

Computadores clássicos são limitados ao pior caso de exatamente ${textstyle lfloor log _{2}n+1rfloor }$ iterações ao executar a pesquisa binária. Algoritmos quânticos para busca binária ainda estão limitados a uma proporção de ${textstyle log _{2}n}$ consultas (representando iterações do procedimento clássico), mas o fator constante é menor do que um, proporcionando uma complexidade de tempo menor em computadores quânticos. Qualquer Exatamente. procedimento de busca quântica binária – ou seja, um procedimento que sempre produz o resultado correto – requer pelo menos ${textstyle {frac {1}{pi }}(ln n-1)approx 0.22log _{2}n}$ consultas no pior caso, onde ${textstyle ln }$ é o logaritmo natural. Há um procedimento de busca binário quântico exato que é executado em ${textstyle 4log _{605}napprox 0.433log _{2}n}$ consultas no pior caso. Em comparação, o algoritmo de Grover é o algoritmo quântico ideal para pesquisar uma lista não ordenada de elementos, e requer $O({sqrt {n}})$ consultas.

História

A ideia de classificar uma lista de itens para permitir uma pesquisa mais rápida remonta à antiguidade. O exemplo mais antigo conhecido foi o tablet Inakibit-Anu da Babilônia que remonta a c. 200 aC. A tabuinha continha cerca de 500 números sexagesimais e seus recíprocos classificados em ordem lexicográfica, o que tornava a busca por uma entrada específica mais fácil. Além disso, várias listas de nomes classificados pela primeira letra foram descobertas nas ilhas do mar Egeu. Catholicon, um dicionário de latim concluído em 1286 EC, foi o primeiro trabalho a descrever regras para classificar palavras em ordem alfabética, em vez de apenas as primeiras letras.

Em 1946, John Mauchly fez a primeira menção à busca binária como parte das Palestras da Escola Moore, um curso universitário seminal e fundamental em computação. Em 1957, William Wesley Peterson publicou o primeiro método de busca por interpolação. Todos os algoritmos de busca binária publicados funcionavam apenas para arrays cujo comprimento é um a menos que uma potência de dois até 1960, quando Derrick Henry Lehmer publicou um algoritmo de busca binária que funcionava em todos os arrays. Em 1962, Hermann Bottenbruch apresentou uma implementação ALGOL 60 de busca binária que colocava a comparação por igualdade no final, aumentando o número médio de iterações em um, mas reduzindo para um o número de comparações por iteração. A busca binária uniforme foi desenvolvida por A. K. Chandra da Universidade de Stanford em 1971. Em 1986, Bernard Chazelle e Leonidas J. Guibas introduziram cascata fracionária como um método para resolver vários problemas de busca em geometria computacional.

Problemas de implementação

Embora a ideia básica da pesquisa binária seja comparativamente direta, os detalhes podem ser surpreendentemente complicados
—Donald Knuth

Quando Jon Bentley atribuiu a pesquisa binária como um problema em um curso para programadores profissionais, ele descobriu que noventa por cento não conseguiu fornecer uma solução correta após várias horas de trabalho, principalmente porque as implementações incorretas falharam ao executar ou retornaram um erro responder em casos extremos raros. Um estudo publicado em 1988 mostra que o código preciso para isso só é encontrado em cinco dos vinte livros didáticos. Além disso, a própria implementação da pesquisa binária de Bentley, publicada em seu livro de 1986 Programming Pearls, continha um erro de estouro que permaneceu sem ser detectado por mais de vinte anos. A implementação da biblioteca de linguagem de programação Java da pesquisa binária teve o mesmo bug de estouro por mais de nove anos.

Em uma implementação prática, as variáveis usadas para representar os índices muitas vezes serão de tamanho fixo (integers), e isso pode resultar em um fluxo aritmético para matrizes muito grandes. Se o ponto médio da extensão for calculado como ${displaystyle {frac {L+R}{2}}}$ , então o valor de $L+R$ pode exceder a gama de inteiros do tipo de dados utilizado para armazenar o ponto médio, mesmo que $L$ e $R$ estão dentro do intervalo. Se $L$ e $R$ são nonnegative, isso pode ser evitado calculando o ponto médio como ${displaystyle L+{frac {R-L}{2}}}$ .

Um loop infinito pode ocorrer se as condições de saída para o loop não forem definidas corretamente. Uma vez. $L$ excede $R$ , a busca falhou e deve transmitir o fracasso da busca. Além disso, o loop deve ser retirado quando o elemento-alvo for encontrado, ou no caso de uma implementação onde este check-in é movido para o fim, verifica se a pesquisa foi bem sucedida ou falhou no final deve estar em vigor. A Bentley descobriu que a maioria dos programadores que implementaram incorretamente a pesquisa binária errou na definição das condições de saída.

Suporte de biblioteca

Muitos idiomas' bibliotecas padrão incluem rotinas de busca binária:

C fornece a função bsearch() em sua biblioteca padrão, que é normalmente implementada através de pesquisa binária, embora o padrão oficial não o exija.
Biblioteca padrão do modelo C++ fornece as funções binary_search(), lower_bound(), upper_bound() e equal_range().
D's standard library Phobos, in std.range módulo fornece um tipo SortedRange (retornado por sort() e assumeSorted() funções) com métodos contains(), equaleRange(), lowerBound() e trisect(), que usam técnicas de pesquisa binárias por padrão para intervalos que oferecem acesso aleatório.
COBOL fornece SEARCH ALL verbo para realizar pesquisas binárias em COBOL ordenou tabelas.
Vai. sort pacote de biblioteca padrão contém as funções Search, SearchInts, SearchFloat64se SearchStrings, que implementam pesquisa binária geral, bem como implementações específicas para pesquisar partes de inteiros, números de ponto flutuante e cordas, respectivamente.
Java oferece um conjunto de sobrecarregados binarySearch() métodos estáticos nas classes Arrays e Collections no padrão java.util pacote para realizar pesquisas binárias em arrays Java e em Lists, respectivamente.
Microsoft's.NET O Framework 2.0 oferece versões genéricas estáticas do algoritmo de busca binário em suas classes de base de coleta. Um exemplo seria System.ArrayMétodo BinarySearch(T[] array, T value).
Para o objectivo-C, o quadro Cocoa fornece NSArray -indexOfObject:inSortedRange:options:usingComparator: método no Mac OS X 10.6+. Fundação Core da Apple C framework também contém CFArrayBSearchValues() Função.
Python fornece o bisect módulo que mantém uma lista em ordem ordenada sem ter que classificar a lista após cada inserção.
A classe Ruby's Array inclui uma bsearch método com combinação aproximada embutida.

Notas e referências

Este artigo foi submetido a WikiJournal of Science para revisão acadêmica externa em 2018 (revisores). O conteúdo atualizado foi reintegrado na página da Wikipédia sob uma licença CC-BY-SA-3.0 (2019). A versão do registro como revisado é: Anthony Lin; et al. (2 de julho de 2019). Algoritmo de pesquisa primária (PDF). WikiJournal of Science. 2 (1): 5. doi:10.15347/WJS/2019.005. ISSN 2470-6345. Wikidata Q81434400.

Contenido relacionado

Más resultados...