Afirmando o conseqüente

Afirmando o consequente, às vezes chamado de erro inverso, falácia do inverso ou confusão de necessidade e suficiência, é uma falácia formal de tomar uma declaração condicional verdadeira (por exemplo, "Se a lâmpada fosse quebrada, então a sala ficaria escura") e inferir inválidamente sua recíproca ("A sala está escura , então a lâmpada está quebrada"), mesmo que essa afirmação não seja verdadeira. Isso ocorre quando um conseqüente ("a sala estaria escura") tem outros antecedentes possíveis (por exemplo, "a lâmpada está funcionando, mas está desligada" ou " não há lâmpada na sala").

Erros de conversação são comuns no pensamento e na comunicação do dia a dia e podem resultar, entre outras causas, de problemas de comunicação, equívocos sobre lógica e falha em considerar outras causas.

A declaração oposta, negando o consequente, é uma forma válida de argumento (modus tollens).

Descrição formal

Existem quatro formas possíveis de silogismos hipotéticos, dois dos quais são válidos, sendo dois inválidos. Considerando um exemplo muito simples pode ajudá-lo a entender por que esses formulários são válidos ou inválidos. Se "p" representa "Candiru é um peixe" e "q" representa "Candiru tem gaivotas", tente convencer-se substituindo estas declarações com p e q na tabela acima.

Afirmar o conseqüente é a ação de tomar uma verdadeira declaração P→ → QNão. P\to Q. e inválida conclusão do seu converso Q→ → PNão. Q\to P}. O nome afirmando o consequente deriva de usar o consequente, Qde P→ → QNão. P\to Q., para concluir o antecedente P. Esta falácia pode ser resumida formalmente como (P→ → Q,Q)→ → P(P\to Q,Q)\to P} ou, alternativamente, P→ → Q,Q∴ ∴ P(P\to Q,Q) P}}}. A causa raiz de tal erro lógico é às vezes falha em perceber que apenas porque P é um possível condição para Q, P não pode ser apenas condição para Q, i.e. Q pode seguir de outra condição também.

Afirmar o conseqüente também pode resultar da sobre generalização da experiência de muitas declarações tendo em conta que verdadeiras conversas. Se P e Q são declarações "equivalentes", ou seja. P↔ ↔ QNão. P\leftrightarrow Q}, o possível de inferir P sob a condição Q. Por exemplo, as declarações "É 13 de agosto, então é meu aniversário" P→ → QNão. P\to Q. e "É meu aniversário, por isso é 13 de agosto" Q→ → PNão. Q\to P} são equivalentes e ambas as consequências verdadeiras da declaração "Agosto 13 é o meu aniversário" (uma forma abreviada de P↔ ↔ QNão. P\leftrightarrow Q}).

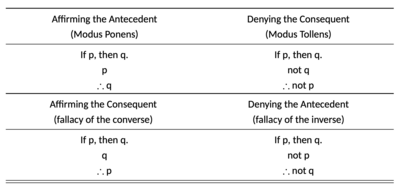
Das possíveis formas de "silogismos hipotéticos mistos" dois são válidos e dois são inválidos. Afirmar o antecedente (modus ponens) e negar o consequente (modus tollens) são válidos. Afirmar o consequente e negar o antecedente são inválidos (ver tabela).

Exemplos adicionais

Exemplo 1

Uma maneira de demonstrar a invalidade dessa forma de argumento é com um contra-exemplo com premissas verdadeiras, mas uma conclusão obviamente falsa. Por exemplo:

Se alguém vive em San Diego, então vivem na Califórnia.

O Joe vive na Califórnia.

Portanto, Joe vive em San Diego.

Existem muitas maneiras de morar na Califórnia sem morar em San Diego, desde que morem em um lugar californiano que não seja San Diego.

No entanto, pode-se afirmar com certeza que "se alguém não mora na Califórnia" (não-Q), então "essa pessoa não mora em San Diego" (não-P). Essa é a contrapositiva da primeira afirmação e deve ser verdadeira se e somente se a afirmação original for verdadeira.

Exemplo 2

Aqui está outro exemplo útil, obviamente falacioso.

Se um animal é um cão, então tem quatro pernas.

O meu gato tem quatro pernas.

Portanto, meu gato é um cão.

Aqui, é imediatamente intuitivo que qualquer número de outros antecedentes ("Se um animal é um cervo...", "Se um animal é um elefante...&#34 ;, "Se um animal é um alce...", etc.) pode dar origem ao consequente ("então tem quatro patas") , e que é absurdo supor que ter quatro patas deve implicar que o animal é um cachorro e nada mais. Isso é útil como exemplo de ensino, pois a maioria das pessoas pode reconhecer imediatamente que a conclusão alcançada deve estar errada (intuitivamente, um gato não pode ser um cachorro) e que o método pelo qual foi alcançado deve, portanto, ser falacioso.

Exemplo 3

Argumentos da mesma forma podem às vezes parecer superficialmente convincentes, como no exemplo a seguir:

Se o Brian tivesse sido expulso da Torre Eiffel, ele estaria morto.

O Brian está morto.

Portanto, Brian foi jogado fora do topo da Torre Eiffel.

Ser jogado do topo da Torre Eiffel não é a única causa de morte, pois existem inúmeras causas diferentes de morte.

Exemplo 4

Em Catch-22, o capelão é interrogado por supostamente ser "Washington Irving"/"Irving Washington", que tem bloqueado grandes porções de soldados' cartas para casa. O coronel encontrou tal carta, mas com o nome do capelão assinado.

"Você pode ler, não pode?" o coronel perseverou sarcasticamente. "O autor assinou o nome dele."

"É o meu nome lá."

"Então você escreveu isso. Q.E.D.

P neste caso é 'O capelão assina seu próprio nome', e Q 'O nome do capelão é escrito'. O nome do capelão pode estar escrito, mas não necessariamente ele o escreveu, como falsamente conclui o coronel.

Exemplo 5

Ao ensinar o método científico, o exemplo a seguir é usado para ilustrar por que, por meio da falácia de afirmar o consequente, nenhuma teoria científica jamais foi comprovada como verdadeira, mas simplesmente falhou em ser falsificada.

Se esta teoria estiver correta, observaremos X.

Observamos X.

Portanto, esta teoria está correta.

Concluir ou presumir que uma teoria é verdadeira por causa de uma previsão que ela fez sendo observada é inválido. Este é um dos desafios da aplicação do método científico, embora raramente seja abordado em contextos acadêmicos, pois é improvável que tenha consequências para os resultados do estudo. Muito mais comum é questionar a validade da teoria, a validade de esperar que a teoria tenha previsto a observação e/ou a validade da própria observação.