Aceleração

Na mecânica, aceleração é a taxa de variação da velocidade de um objeto em relação ao tempo. As acelerações são grandezas vetoriais (pois têm magnitude e direção). A orientação da aceleração de um objeto é dada pela orientação da força líquida que age sobre esse objeto. A magnitude da aceleração de um objeto, conforme descrito pela Segunda Lei de Newton, é o efeito combinado de duas causas:

• o equilíbrio líquido de todas as forças externas que atuam nesse objeto — a magnitude é diretamente proporcional a essa força resultante da rede;
• massa desse objeto, dependendo dos materiais de que é feito — a magnitude é inversamente proporcional à massa do objeto.

A unidade SI para aceleração é metro por segundo quadrado (M⋅s^-2, ${displaystyle mathrm {tfrac} Não.$).

Por exemplo, quando um veículo parte de uma paralisação (velocidade zero, em um referencial inercial) e viaja em linha reta a velocidades crescentes, ele está acelerando na direção da viagem. Se o veículo virar, ocorre uma aceleração em direção à nova direção e altera seu vetor de movimento. A aceleração do veículo em sua direção atual de movimento é chamada de aceleração linear (ou tangencial durante movimentos circulares), a reação à qual os passageiros a bordo experimentam como uma força que os empurra de volta para seus assentos. Ao mudar de direção, a aceleração efetiva é chamada de aceleração radial (ou centrípeta durante movimentos circulares), a reação à qual os passageiros experimentam como uma força centrífuga. Se a velocidade do veículo diminuir, trata-se de uma aceleração na direção oposta e matematicamente negativa, às vezes chamada de desaceleração ou retardo, e os passageiros experimentam a reação à desaceleração como um força de inércia empurrando-os para frente. Essas acelerações negativas são frequentemente alcançadas pela queima de retrofoguetes em espaçonaves. Tanto a aceleração quanto a desaceleração são tratadas da mesma forma, pois ambas são mudanças na velocidade. Cada uma dessas acelerações (tangencial, radial, desaceleração) é sentida pelos passageiros até que sua velocidade relativa (diferencial) seja neutralizada em relação à aceleração devido à mudança de velocidade.

Definição e propriedades

Quantidades kinemáticas de uma partícula clássica: massa m, posição R, velocidade v, aceleração um.

Aceleração média

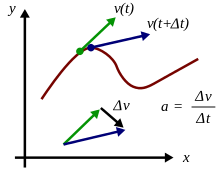
Aceleração é a taxa de mudança de velocidade. Em qualquer ponto sobre uma trajetória, a magnitude da aceleração é dada pela taxa de mudança de velocidade em ambas as magnitudes e direção nesse ponto. A verdadeira aceleração no tempo ) é encontrado no limite como intervalo de tempo ?) → 0 de ?v- Não.)

A aceleração média de um objeto ao longo de um período de tempo é sua mudança na velocidade, $Não. Delta mathbf {v} }$, dividido pela duração do período, ${displaystyle Delta t}$. Matematicamente,

$$Não. - Sim. Não. Delta t}}.$$

Aceleração instantânea

Do fundo ao topo:

• uma função de aceleração um());
• a integral da aceleração é a função de velocidade v());
• e a integral da velocidade é a função de distância S()).

A aceleração instantânea, por sua vez, é o limite da aceleração média em um intervalo de tempo infinitesimal. Em termos de cálculo, a aceleração instantânea é a derivada do vetor velocidade em relação ao tempo:

$${displaystyle mathbf {a} =lim _{{Delta t}to 0}{frac Não. }{Delta t}}={frac {dmathbf} ?$$

$${displaystyle mathbf {a} ? }{dt}}={frac {d^{2}mathbf {x} }{dt^{2}}$$

(Aqui e em outros lugares, se o movimento for em linha reta, as quantidades vetoriais podem ser substituídas por escalares nas equações.)

Pelo teorema fundamental do cálculo, pode-se ver que a integral da função de aceleração a(t) é a função de velocidade v(t); ou seja, a área sob a curva de uma aceleração versus tempo (estilo a vs. estilo t) gráfico corresponde à mudança de velocidade.

$${displaystyle mathbf {Delta v} =int mathbf {a} ,dt}$$

Da mesma forma, a integral da função jerk j(t), a derivada da função de aceleração, pode ser usado para encontrar a mudança de aceleração em um determinado momento:

$${displaystyle mathbf {Delta a} =int mathbf {j} ,dt}$$

Unidades

A aceleração tem as dimensões da velocidade (L/T) dividida pelo tempo, ou seja, L T⁻². A unidade SI de aceleração é o metro por segundo ao quadrado (m s⁻²); ou "metro por segundo por segundo", pois a velocidade em metros por segundo muda pelo valor da aceleração, a cada segundo.

Outras formas

Um objeto que se move em um movimento circular, como um satélite orbitando a Terra, está acelerando devido à mudança de direção do movimento, embora sua velocidade possa ser constante. Neste caso, diz-se que está em aceleração centrípeta (direcionada para o centro).

A aceleração adequada, a aceleração de um corpo em relação a uma condição de queda livre, é medida por um instrumento chamado acelerômetro.

Na mecânica clássica, para um corpo com massa constante, a aceleração (vetorial) do centro de massa do corpo é proporcional ao vetor de força resultante (ou seja, a soma de todas as forças) atuando sobre ele (segunda lei de Newton):

$${displaystyle mathbf {F} =mmathbf {a} quad implies quad mathbf {a} ={frac {mathbf Não.$$

Aceleração tangencial e centrípeta

Um pêndulo oscilante, com velocidade e aceleração marcadas. Ele experimenta a aceleração tangencial e centrípeta.

Componentes de aceleração para um movimento curvo. O componente tangencial um₎ é devido à mudança na velocidade de traversal, e pontos ao longo da curva na direção do vetor de velocidade (ou na direção oposta). O componente normal (também chamado componente centrípeto para movimento circular) um_c é devido à mudança na direção do vetor de velocidade e é normal para a trajetória, apontando para o centro da curvatura do caminho.

A velocidade de uma partícula movendo-se em uma trajetória curva em função do tempo pode ser escrita como:

$${displaystyle mathbf {v} (t)=v(t){frac {mathbf {v} (t)}{v(t)}}=v(t)mathbf {u} _{mathrm {t} }(t),}$$

$${displaystyle mathbf {u} - Sim.$$

$${displaystyle {begin{alignedat}{3}mathbf {a} &={frac {dmathbf {v} frac{dt}}&={frac {dv}{dt}}mathbf {u} _{mathrm {t} }+v(t){frac {dmathbf {u} - Sim. frac{dt}}&={frac {dv}{dt}}mathbf {u} _{mathrm {t} }+{frac {v^{2}}{r}}mathbf {u} _{mathrm {n} }\end{alignedat}}}$$

onde u_n é o vetor normal unitário (para dentro) para a trajetória da partícula (também chamado o normal principal), e r é seu raio instantâneo de curvatura baseado no círculo osculador no tempo t. Esses componentes são chamados de aceleração tangencial e aceleração normal ou radial (ou aceleração centrípeta em movimento circular, veja também movimento circular e força centrípeta).

A análise geométrica de curvas espaciais tridimensionais, que explica a tangente, (principal) normal e binormal, é descrita pelas fórmulas de Frenet–Serret.

Casos especiais

Aceleração uniforme

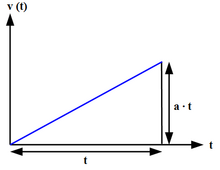
Cálculo da diferença de velocidade para uma aceleração uniforme

uniforme ou constante é um tipo de movimento no qual a velocidade de um objeto muda em uma quantidade igual em cada período de tempo igual.

Um exemplo frequentemente citado de aceleração uniforme é o de um objeto em queda livre em um campo gravitacional uniforme. A aceleração de um corpo em queda na ausência de resistências ao movimento é dependente apenas da força de campo gravitacional g (também chamado de aceleração devido à gravidade). Pela Segunda Lei de Newton a força ${displaystyle mathbf {F_{g}} }$ agir em um corpo é dado por:

$${displaystyle mathbf {F_{g}} =mmathbf {g} } }$$

Devido às propriedades analíticas simples do caso de aceleração constante, existem fórmulas simples que relacionam o deslocamento, as velocidades iniciais e dependentes do tempo e a aceleração com o tempo decorrido:

$${displaystyle {begin{aligned}mathbf {s} (t)&=mathbf {s}) _{0}+mathbf {v} _{0}t+{tfrac {1}{2}}mathbf {a} t^{2}=mathbf {s} _{0}+{tfrac {1}{2}}left(mathbf {v} _{0}+mathbf {v} (t)right)t\mathbf {v} (t)&=mathbf {v} _{0}+mathbf {a} t{v^{2}}(t)&={v_{0}}^{2}+2mathbf {acdot } [mathbf {s} (t)-mathbf {s} _{0}]end{aligned}}}}$$

onde

• $Não.$ é o tempo decorrido,
• ${displaystyle mathbf {s} _{0}}$ é o deslocamento inicial da origem,
• $(t)}$ é o deslocamento da origem no momento $Não.$,
• $(v) _{0}}$ é a velocidade inicial,
• $(t)}$ é a velocidade no momento $Não.$e
• ${displaystyle mathbf {a} } }$ é a taxa uniforme de aceleração.

Em particular, o movimento pode ser dividido em duas partes ortogonais, uma de velocidade constante e a outra de acordo com as equações acima. Como Galileu mostrou, o resultado líquido é o movimento parabólico, que descreve, por exemplo, a trajetória de um projétil no vácuo perto da superfície da Terra.

Movimento circular

Vetor de posição R, sempre aponta radialmente da origem.

Vetor de velocidade v, sempre tangente ao caminho do movimento.

Vetor de aceleração um, não paralelo ao movimento radial, mas compensado pelas acelerações angulares e Coriolis, nem tangente ao caminho, mas compensado pelas acelerações centrípetas e radiais.

Vetores kinemáticos em coordenadas polares planas. Observe que a configuração não é restrita ao espaço 2d, mas pode representar o plano de plano de oscilação em um ponto de uma curva arbitrária em qualquer dimensão superior.

No movimento circular uniforme, isto é, movendo-se com velocidade constante ao longo de uma trajetória circular, uma partícula experimenta uma aceleração resultante da mudança da direção do vetor velocidade, enquanto seu módulo permanece constante. A derivada da localização de um ponto em uma curva em relação ao tempo, ou seja, sua velocidade, acaba sendo sempre exatamente tangente à curva, respectivamente ortogonal ao raio neste ponto. Como no movimento uniforme a velocidade na direção tangencial não varia, a aceleração deve ser na direção radial, apontando para o centro do círculo. Essa aceleração muda constantemente a direção da velocidade para ser tangente no ponto vizinho, girando assim o vetor velocidade ao longo do círculo.

• Para uma velocidade dada $Não.$, a magnitude desta aceleração geometricamente causada (aceleração centrípeta) é inversamente proporcional ao raio $Não.$ do círculo, e aumenta como o quadrado desta velocidade:
  $$Não. a_{c}={frac {v^{2}}{r}},.}$$

  
• Note que, para uma dada velocidade angular $- Sim.$, a aceleração centrípeta é diretamente proporcional ao raio $Não.$. Isto é devido à dependência da velocidade $Não.$ no raio $Não.$.
  $$Não.$$

  

Expressando vetor de aceleração centrípeta em componentes polares, onde $- Sim.$ é um vetor do centro do círculo para a partícula com magnitude igual a esta distância, e considerando a orientação da aceleração para o centro, rende

$${displaystyle mathbf {a_{c}} =-{frac {v^{2}}{|mathbf {r} |}}cdot Não. |{|mathbf {r} |}},.}$$

Como de costume em rotações, a velocidade $Não.$ de uma partícula pode ser expressa como uma velocidade angular em relação a um ponto à distância $Não.$ como

$${displaystyle omega ={frac Não.$$

Assim ${displaystyle mathbf {a_{c}} =-omega ^{2}mathbf {r} ,.}$

Esta aceleração e a massa da partícula determinam a força centrípeta necessária, dirigida em direção ao centro do círculo, como a força resultante que atua sobre esta partícula para mantê-la neste movimento circular uniforme. A chamada 'força centrífuga', parecendo agir externamente sobre o corpo, é a chamada pseudoforça experimentada no quadro de referência do corpo em movimento circular, devido ao movimento do corpo. momento linear, um vetor tangente ao círculo do movimento.

Em um movimento circular não uniforme, ou seja, a velocidade ao longo do caminho curvo está mudando, a aceleração tem um componente não-zero tangencial para a curva, e não se limita ao principal normal, que dirige ao centro do círculo oscilante, que determina o raio $Não.$ para a aceleração centrípeta. O componente tangencial é dado pela aceleração angular $- Sim.$, ou seja, a taxa de mudança ${displaystyle alpha ={dot {omega)$ da velocidade angular $- Sim.$ vezes o raio $Não.$. Isso é,

$$Não. a_{t}=ralpha.}$$

O sinal do componente tangencial da aceleração é determinado pelo sinal da aceleração angular ($- Sim.$), e o tangente é sempre direcionado para ângulos retos para o vetor de raio.

Relação com a relatividade

Relatividade especial

A teoria especial da relatividade descreve o comportamento de objetos viajando em relação a outros objetos em velocidades próximas à da luz no vácuo. A mecânica newtoniana é exatamente revelada como uma aproximação da realidade, válida com grande precisão em velocidades mais baixas. À medida que as velocidades relevantes aumentam em direção à velocidade da luz, a aceleração não segue mais as equações clássicas.

À medida que as velocidades se aproximam da velocidade da luz, a aceleração produzida por uma determinada força diminui, tornando-se infinitesimalmente pequena à medida que a velocidade da luz se aproxima; um objeto com massa pode se aproximar dessa velocidade assintoticamente, mas nunca alcançá-la.

Relatividade geral

A menos que o estado de movimento de um objeto seja conhecido, é impossível distinguir se uma força observada é devida à gravidade ou à aceleração - a gravidade e a aceleração inercial têm efeitos idênticos. Albert Einstein chamou isso de princípio da equivalência e disse que apenas os observadores que não sentem nenhuma força — incluindo a força da gravidade — podem concluir que não estão acelerando.

Conversões