Aberração (astronomia)
Na astronomia, aberração (também conhecida como aberração astronômica, aberração estelar ou aberração de velocidade) é um fenômeno que produz um movimento aparente de objetos celestes sobre suas verdadeiras posições, dependente da velocidade do observador. Faz com que os objetos pareçam estar deslocados na direção do movimento do observador em comparação com quando o observador está parado. A mudança no ângulo é da ordem de v/c onde c é a velocidade da luz e v a velocidade do observador. No caso de "estelar" ou "anual" aberração, a posição aparente de uma estrela para um observador na Terra varia periodicamente ao longo de um ano à medida que a velocidade da Terra muda à medida que gira em torno do Sol, por um ângulo máximo de aproximadamente 20 segundos de arco em ascensão reta ou declinação.
O termo aberração tem sido historicamente usado para se referir a uma série de fenômenos relacionados à propagação da luz em corpos em movimento. Aberração é diferente de paralaxe, que é uma mudança na posição aparente de um objeto relativamente próximo, medida por um observador em movimento, em relação a objetos mais distantes que definem um quadro de referência. A quantidade de paralaxe depende da distância do objeto ao observador, enquanto a aberração não. A aberração também está relacionada à correção de tempo de luz e irradiação relativística, embora muitas vezes seja considerada separadamente desses efeitos.
A aberração é historicamente significativa devido ao seu papel no desenvolvimento das teorias da luz, do eletromagnetismo e, finalmente, da teoria da relatividade especial. Foi observado pela primeira vez no final de 1600 por astrônomos em busca de paralaxe estelar para confirmar o modelo heliocêntrico do Sistema Solar. No entanto, não foi entendido na época como um fenômeno diferente. Em 1727, James Bradley forneceu uma explicação clássica para isso em termos da velocidade finita da luz em relação ao movimento da Terra em sua órbita ao redor do Sol, que ele usou para fazer uma das primeiras medições da velocidade da luz. No entanto, a teoria de Bradley era incompatível com as teorias da luz do século XIX, e a aberração tornou-se uma grande motivação para as teorias de arrasto do éter de Augustin Fresnel (em 1818) e G. G. Stokes (em 1845), e para Hendrik Lorentz' A teoria do éter do eletromagnetismo em 1892. A aberração da luz, juntamente com a elaboração de Lorentz da eletrodinâmica de Maxwell, o problema do ímã em movimento e do condutor, os experimentos de deriva do éter negativo, bem como o experimento de Fizeau, levaram Albert Einstein para desenvolver a teoria da relatividade especial em 1905, que apresenta uma forma geral da equação para aberração em termos de tal teoria.
Explicação
A aberração pode ser explicada como a diferença no ângulo de um feixe de luz em diferentes referenciais inerciais. Uma analogia comum é considerar a direção aparente da chuva que cai. Se a chuva está caindo verticalmente no quadro de referência de uma pessoa parada, para uma pessoa que se move para frente a chuva parecerá chegar em um ângulo, exigindo que o observador em movimento incline seu guarda-chuva para frente. Quanto mais rápido o observador se move, mais inclinação é necessária.
O efeito líquido é que os raios de luz que atingem o observador em movimento pelos lados em um referencial estacionário virão em ângulo à frente no referencial do observador em movimento. Esse efeito às vezes é chamado de "holofote" ou "farol" efeito.
No caso de aberração anual da luz estelar, a direção da entrada da luz estelar vista no referencial móvel da Terra é inclinada em relação ao ângulo observado no referencial do Sol. Como a direção do movimento da Terra muda durante sua órbita, a direção dessa inclinação muda durante o curso do ano e faz com que a posição aparente da estrela seja diferente de sua verdadeira posição medida no referencial inercial do Sol.
Embora o raciocínio clássico dê intuição para a aberração, ele leva a uma série de paradoxos físicos observáveis até mesmo no nível clássico (ver história). A teoria da relatividade especial é necessária para explicar corretamente a aberração. A explicação relativística é muito semelhante à clássica, porém, e em ambas as teorias a aberração pode ser entendida como um caso de adição de velocidades.
Explicação clássica
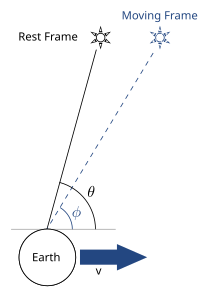
No quadro do Sol, considere um feixe de luz com velocidade igual à velocidade de luz c, com componentes de velocidade x e y ux{displaystyle u_{x}} e uSim.Não. U_{y}}, e assim em um ângulo θ tal que bronzeado (θ θ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =uSim./ux{displaystyle tan(theta)=u_{y}/u_{x}}. Se a Terra está se movendo em velocidade vNão. na direção x relativa ao Sol, então por adição de velocidade o componente x da velocidade do feixe no quadro de referência da Terra é ux?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ux+vNão. u_{x}'=u_{x}+v}, e a velocidade y é inalterada, uSim.?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =uSim.Não. u_{y}'=u_{y}}. Assim, o ângulo da luz no quadro da Terra em termos do ângulo no quadro do Sol é
- bronzeado (φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =uSim.?ux?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =uSim.ux+v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =pecado (θ θ )v/c+e (θ θ ){displaystyle tan(phi)={frac {u_{y}'{u_{x}'}}={frac {u_{y}}{u_{x}+v}}={frac {sin(theta)}{v/c+cos(theta)}}}
No caso de θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =90∘ ∘ {displaystyle theta =90^{circ), este resultado reduz a bronzeado (θ θ - Sim. - Sim. φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v/c{displaystyle tan(theta -phi)=v/c}, que no limite v/c≪ ≪ 1{displaystyle v/cll 1} pode ser aproximado por θ θ - Sim. - Sim. φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v/c{displaystyle theta -phi =v/c}.
Explicação relativística
O raciocínio no caso relativístico é o mesmo, exceto que as fórmulas de adição de velocidade relativística devem ser usadas, que podem ser derivadas de transformações de Lorentz entre diferentes sistemas de referência. Estas fórmulas são
- ux?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(ux+v)/(1+uxv/c2)(u_{x}+v)/(1+u_{x}v/c^{2})}
- uSim.?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =uSim./γ γ (1+uxv/c2)Não. u_{y}'=u_{y}/gamma (1+u_{x}v/c^{2})}
Onde? γ γ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1/1- Sim. - Sim. v2/c2{displaystyle gamma =1/{sqrt {1-v^{2}/c^{2}}, dando os componentes do feixe de luz no quadro da Terra em termos dos componentes no quadro do Sol. O ângulo do feixe no quadro da Terra é assim
- bronzeado (φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =uSim.?ux?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =uSim.γ γ (ux+v)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =pecado (θ θ )γ γ (v/c+e (θ θ )){displaystyle tan(phi)={frac {u_{y}'{u_{x}'}}={frac {u_{y}}{gamma (u_{x}+v)}}={frac {sin(theta)}{gamma (v/c+cos(theta)}}}
No caso de θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =90∘ ∘ {displaystyle theta =90^{circ), este resultado reduz a pecado (θ θ - Sim. - Sim. φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v/c{displaystyle sin(theta -phi)=v/c}, e no limite v/c≪ ≪ 1{displaystyle v/cll 1} isto pode ser aproximado por θ θ - Sim. - Sim. φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v/c{displaystyle theta -phi =v/c}. Esta derivação relativista mantém a velocidade da luz ux2+uSim.2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =c{displaystyle {sqrt {u_{x}^{2}+u_{y}^{2}}}=c} constante em todos os quadros de referência, ao contrário da derivação clássica acima.
Relação com correção de tempo de luz e irradiação relativística
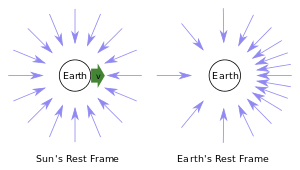
A aberração está relacionada a dois outros fenômenos, a correção do tempo de luz, que ocorre devido ao movimento de um objeto observado durante o tempo que sua luz leva para chegar a um observador, e o feixe relativístico, que é um ângulo da luz emitida por uma fonte de luz em movimento. Pode ser considerado equivalente a eles, mas em um referencial inercial diferente. Na aberração, considera-se que o observador está se movendo em relação a uma fonte de luz estacionária (para simplificar), enquanto na correção de tempo de luz e radiação relativística a fonte de luz é considerada em movimento em relação a um observador estacionário.
Considere o caso de um observador e uma fonte de luz movendo-se um em relação ao outro em velocidade constante, com um feixe de luz movendo-se da fonte para o observador. No momento da emissão, o feixe no referencial de repouso do observador é inclinado em relação ao do referencial de repouso da fonte, conforme entendido por irradiação relativística. Durante o tempo que o feixe de luz leva para alcançar o observador, a fonte de luz se move no quadro do observador e a 'posição real' da fonte de luz é deslocado em relação à posição aparente que o observador vê, conforme explicado pela correção do tempo de luz. Finalmente, o feixe no referencial do observador no momento da observação é inclinado em relação ao feixe no referencial da fonte, o que pode ser entendido como um efeito aberrante. Assim, uma pessoa no enquadramento da fonte de luz descreveria a inclinação aparente do feixe em termos de aberração, enquanto uma pessoa no enquadramento do observador a descreveria como um efeito de tempo de luz.
A relação entre esses fenômenos só é válida se os referenciais do observador e da fonte forem referenciais inerciais. Na prática, como a Terra não é um referencial de repouso inercial, mas experimenta aceleração centrípeta em direção ao Sol, muitos efeitos aberracionais, como a aberração anual na Terra, não podem ser considerados correções luz-tempo. No entanto, se o tempo entre a emissão e a detecção da luz for curto em comparação com o período orbital da Terra, a Terra pode ser aproximada como um referencial inercial e os efeitos aberracionais são equivalentes às correções luz-tempo.
Tipos
O Almanaque Astronômico descreve vários tipos diferentes de aberração, decorrentes de diferentes componentes do movimento da Terra e do objeto observado:
- Aberração estelar: "O deslocamento angular aparente da posição observada de um corpo celestial resultante do movimento do observador. A aberração estelar é dividida em componentes diurnais, anuais e seculares."
- Aberração anual: "O componente da aberração estelar resultante do movimento da Terra sobre o Sol."
- Aberração diurna: "O componente da aberração estelar resultante do movimento diurnal do observador sobre o centro da Terra devido à rotação da Terra."
- Aberração secular: "O componente da aberração estelar resultante do movimento essencialmente uniforme e quase rectilinear de todo o sistema solar no espaço. A aberração secular é geralmente desconsiderada."
- Aberração planetária: "O deslocamento angular aparente da posição observada de um corpo do sistema solar de sua direção geocêntrica instantânea como seria visto por um observador no geocentro. Este deslocamento é causado pela aberração de deslocamento leve e leve."
Aberração anual

A aberração anual é causada pelo movimento de um observador na Terra enquanto o planeta gira em torno do Sol. Devido à excentricidade orbital, a velocidade orbital vNão. da Terra (no resto do Sol) varia periodicamente durante o ano quando o planeta atravessa sua órbita elíptica e, consequentemente, a aberração também varia periodicamente, tipicamente fazendo com que as estrelas pareçam se mover em pequenas elipses.
Aproximando a órbita da Terra como circular, o deslocamento máximo de uma estrela devido à aberração anual é conhecido como a constante de aberração, representado convencionalmente por κ κ - Sim.. Pode ser calculado usando a relação κ κ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =θ θ - Sim. - Sim. φ φ ? ? v/c{displaystyle kappa =theta -phi approx v/c} substituindo a velocidade média da Terra no quadro do Sol para vNão. e a velocidade da luz cNão.. Seu valor aceito é 20.49552 segundos de arco (sec) ou 0,000099365 radianos (rad) (em J2000).
Assumindo uma órbita circular, a aberração anual faz com que as estrelas exatamente na eclíptica (o plano da órbita da Terra) pareçam mover-se para trás e para frente ao longo de uma linha reta, variando por κ κ - Sim. de cada lado da sua posição no quadro do Sol. Uma estrela que está precisamente em um dos polos eclípticos (a 90° do plano eclíptico) aparecerá para se mover em um círculo de raio κ κ - Sim. sobre sua posição verdadeira, e estrelas em latitudes eclípticas intermediárias aparecerão para mover ao longo de uma pequena elipse.
Para ilustrar, considere uma estrela no polo eclíptico norte visto por um observador em um ponto no Círculo Ártico. Tal observador verá o trânsito da estrela no zenith, uma vez todos os dias (realmente falando dia sideral). No momento do equinócio de março, a órbita da Terra carrega o observador em uma direção para o sul, e a declinação aparente da estrela é, portanto, deslocada para o sul por um ângulo de κ κ - Sim.. No equinócio de setembro, a posição da estrela é deslocada para o norte por uma quantidade igual e oposta. Em qualquer solstício, o deslocamento na declinação é 0. Por outro lado, a quantidade de deslocamento na ascensão direita é 0 em qualquer equinócio e no máximo em qualquer solstício.
Na verdade, a órbita da Terra é ligeiramente elíptica em vez de circular, e sua velocidade varia um pouco ao longo de sua órbita, o que significa que a descrição acima é apenas aproximada. A aberração é calculada com mais precisão usando a velocidade instantânea da Terra em relação ao baricentro do Sistema Solar.
Observe que o deslocamento devido à aberração é ortogonal a qualquer deslocamento devido à paralaxe. Se a paralaxe for detectável, o deslocamento máximo para o sul ocorreria em dezembro e o deslocamento máximo para o norte em junho. É esse movimento aparentemente anômalo que tanto mistificou os primeiros astrônomos.
Aberração solar anual
Um caso especial de aberração anual é a deflexão quase constante do Sol de sua posição no resto do Sol por κ κ - Sim. para a Oeste (como visto da Terra), em frente ao movimento aparente do Sol ao longo da eclíptica (que é de oeste a leste, como visto da Terra). A deflexão faz com que o Sol pareça estar por trás (ou retardado) de sua posição de descanso na eclíptica por uma posição ou ângulo κ κ - Sim..
Esta deflexão pode ser equivalentemente descrita como um efeito leve devido ao movimento da Terra durante os 8.3 minutos que leva luz para viajar do Sol para a Terra. A relação com κ κ - Sim. é: [0,000099365 rad / 2 π rad] x [365.25 d x 24 h/d x 60 min/h] = 8.3167 min ≈ 8 min 19 sec = 499 sec. Isso é possível, uma vez que o tempo de trânsito da luz solar é curto em relação ao período orbital da Terra, então o quadro da Terra pode ser aproximado como inercial. No quadro da Terra, o Sol se move, a uma velocidade média v = 29.789 km/s, por uma distância ? ? x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v)Não. Delta x=vt ≈ 14,864.7 km no tempo que leva luz para chegar à Terra, )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R/cNão. T=R/c ≈ 499 sec para a órbita do raio médio RNão. R. = 1 UA = 149,597,870.7 km. Isso dá uma correção angular bronzeado (θ θ )? ? θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? x/R{displaystyle tan(theta)approx theta =Delta x/R} ≈ 0,000099364 rad = 20.49539 sec, que pode ser resolvido para dar θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v/c= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =κ κ {displaystyle theta - Sim. ≈ 0,000099365 rad = 20.49559 sec, muito quase o mesmo que a correção aberrativa (aqui κ κ - Sim. está em radiano e não em segundo de arco).
Aberração diurna
A aberração diurna é causada pela velocidade do observador na superfície da Terra em rotação. Portanto, depende não apenas da hora da observação, mas também da latitude e longitude do observador. Seu efeito é muito menor que o da aberração anual e é de apenas 0,32 segundo de arco no caso de um observador no Equador, onde a velocidade de rotação é maior.
Aberração secular
O componente secular da aberração, causado pelo movimento do Sistema Solar no espaço, foi ainda subdividido em vários componentes: aberração resultante do movimento do baricentro do sistema solar em torno do centro da nossa Galáxia, aberração resultante do movimento da Galáxia em relação ao Grupo Local, e a aberração resultante do movimento do Grupo Local em relação à radiação cósmica de fundo. A aberração secular afeta as posições aparentes de estrelas e objetos extragalácticos. A parte grande e constante da aberração secular não pode ser observada diretamente e "Tem sido uma prática padrão absorver esse efeito grande e quase constante no relatado" posições das estrelas.
Em cerca de 200 milhões de anos, o Sol circunda o centro galáctico, cuja localização medida é próxima da ascensão reta (α = 266,4°) e da declinação (δ = −29,0°). O efeito constante e inobservável do movimento do sistema solar em torno do centro galáctico foi calculado variadamente como 150 ou 165 segundos de arco. A outra parte, observável, é uma aceleração em direção ao centro galáctico de aproximadamente 2,5 × 10−10 m/s2, que produz uma mudança de aberração de cerca de 5 µas/ ano Medições altamente precisas que se estendem por vários anos podem observar essa mudança na aberração secular, muitas vezes chamada de deriva da aberração secular ou aceleração do Sistema Solar, como um pequeno movimento próprio aparente.
Recentemente, a astrometria altamente precisa de objetos extragalácticos usando a interferometria de linha de base muito longa e o observatório espacial Gaia mediram com sucesso esse pequeno efeito. A primeira medição VLBI do movimento aparente, durante um período de 20 anos, de 555 objetos extragalácticos em direção ao centro de nossa galáxia em coordenadas equatoriais de α = 263° e δ = −20° indicou uma deriva de aberração secular 6,4 ±1,5 μas/ ano Determinações posteriores usando uma série de medições de VLBI que se estendem por quase 40 anos determinaram que o desvio da aberração secular era de 5,83 ± 0,23 μas/ano na direção α = 270,2 ± 2,3° e δ = −20,2° ± 3,6°. Observações ópticas usando apenas 33 meses de dados do satélite Gaia de 1,6 milhão de fontes extragalácticas indicaram uma aceleração do sistema solar de 2,32 ± 0,16 × 10−10 m/s 2 e um desvio de aberração secular correspondente de 5,05 ± 0,35 µas/ano na direção de α = 269,1° ± 5,4°, δ = −31,6° ± 4,1°. Espera-se que lançamentos posteriores de dados do Gaia, incorporando cerca de 66 e 120 meses de dados, reduzam os erros aleatórios desses resultados por fatores de 0,35 e 0,15. A edição mais recente do Quadro de Referência Celestial Internacional (ICRF3) adotou uma constante de aberração galactocêntrica recomendada de 5,8 µas/ano e recomendou uma correção para aberração secular para obter a maior precisão posicional para tempos diferentes da época de referência 2015.0.
Aberração planetária
A aberração planetária é a combinação da aberração da luz (devido à velocidade da Terra) e da correção do tempo de luz (devido ao movimento e à distância do objeto), conforme calculado no quadro restante do Sistema solar. Ambos são determinados no instante em que a luz do objeto em movimento atinge o observador em movimento na Terra. É assim chamado porque geralmente é aplicado a planetas e outros objetos do Sistema Solar cujo movimento e distância são conhecidos com precisão.
Descoberta e primeiras observações
A descoberta da aberração da luz foi totalmente inesperada, e foi apenas por considerável perseverança e perspicácia que Bradley foi capaz de explicá-la em 1727. Originou-se de tentativas de descobrir se as estrelas possuíam paralaxes apreciáveis.
Procure por paralaxe estelar
A teoria heliocêntrica copernicana do Sistema Solar foi confirmada pelas observações de Galileu e Tycho Brahe e pelas investigações matemáticas de Kepler e Newton. Já em 1573, Thomas Digges havia sugerido que o deslocamento paralático das estrelas deveria ocorrer de acordo com o modelo heliocêntrico e, consequentemente, se a paralaxe estelar pudesse ser observada, isso ajudaria a confirmar essa teoria. Muitos observadores alegaram ter determinado tais paralaxes, mas Tycho Brahe e Giovanni Battista Riccioli concluíram que elas existiam apenas nas mentes dos observadores e eram devidas a erros instrumentais e pessoais. No entanto, em 1680 Jean Picard, em sua Voyage d'Uranibourg, afirmou, como resultado de dez anos' observações, que Polaris, a estrela polar, exibiu variações em sua posição no valor de 40″ anualmente. Alguns astrônomos tentaram explicar isso pela paralaxe, mas essas tentativas falharam porque o movimento era diferente daquele que a paralaxe produziria. John Flamsteed, a partir de medições feitas em 1689 e nos anos seguintes com seu quadrante mural, concluiu de forma semelhante que a declinação de Polaris era 40″ menor em julho do que em setembro. Robert Hooke, em 1674, publicou suas observações de γ Draconis, uma estrela de magnitude 2m que passa praticamente acima na latitude de Londres (portanto, suas observações são amplamente livres de correções complexas devido à refração atmosférica), e concluiu que esta estrela estava 23″ mais ao norte em julho do que em outubro.
Observações de James Bradley
Consequentemente, quando Bradley e Samuel Molyneux entraram nesta esfera de pesquisa em 1725, ainda havia uma incerteza considerável sobre se paralaxes estelares haviam sido observadas ou não, e foi com a intenção de responder definitivamente a esta questão que eles ergueram um grande telescópio na casa de Molyneux em Kew. Eles decidiram reinvestigar o movimento de γ Draconis com um telescópio construído por George Graham (1675-1751), um célebre fabricante de instrumentos. Este foi fixado a uma chaminé vertical de maneira a permitir uma pequena oscilação da ocular, cuja quantidade (ou seja, o desvio da vertical) foi regulada e medida pela introdução de um parafuso e um fio de prumo.
O instrumento foi montado em novembro de 1725, e as observações sobre γ Draconis foram feitas a partir de dezembro. Observou-se que a estrela se moveu 40″ para o sul entre setembro e março, e então inverteu seu curso de março para setembro. Ao mesmo tempo, 35 Camelopardalis, uma estrela com uma ascensão reta quase exatamente oposta à de γ Draconis, tinha 19" mais ao norte no início de março do que em setembro. Esses resultados foram completamente inesperados e inexplicáveis pelas teorias existentes.
Hipóteses iniciais
Bradley e Molyneux discutiram várias hipóteses na esperança de encontrar a solução. Como o movimento aparente não foi evidentemente causado por paralaxe nem por erros de observação, Bradley primeiro levantou a hipótese de que poderia ser devido a oscilações na orientação do eixo da Terra em relação à esfera celeste - um fenômeno conhecido como nutação. 35 Camelopardalis foi visto como possuindo um movimento aparente que poderia ser consistente com a nutação, mas como sua declinação variava apenas metade da de γ Draconis, era óbvio que a nutação não fornecia a resposta (no entanto, Bradley mais tarde passou a descobrir que a Terra realmente nuta). Ele também investigou a possibilidade de o movimento ser devido a uma distribuição irregular da atmosfera terrestre, envolvendo variações anormais no índice de refração, mas novamente obteve resultados negativos.
Em 19 de agosto de 1727, Bradley embarcou em uma nova série de observações usando um telescópio de sua autoria erguido na Reitoria, Wanstead. Este instrumento tinha a vantagem de um campo de visão maior e ele foi capaz de obter posições precisas de um grande número de estrelas ao longo de cerca de vinte anos. Durante seus primeiros dois anos em Wanstead, ele estabeleceu a existência do fenômeno da aberração além de qualquer dúvida, e isso também lhe permitiu formular um conjunto de regras que permitiriam o cálculo do efeito em qualquer estrela em uma data especificada.
Desenvolvimento da teoria da aberração
Bradley finalmente desenvolveu sua explicação da aberração por volta de setembro de 1728 e essa teoria foi apresentada à Royal Society em meados de janeiro do ano seguinte. Uma história bem conhecida é que ele viu a mudança de direção de um cata-vento em um barco no Tâmisa, causada não por uma alteração do próprio vento, mas por uma mudança de curso do barco em relação à direção do vento. No entanto, não há registro desse incidente no próprio relato de Bradley sobre a descoberta e, portanto, pode ser apócrifo.
A tabela a seguir mostra a magnitude do desvio da declinação verdadeira para γ Draconis e a direção, nos planos da colura solsticial e meridiano principal eclíptico, da tangente da velocidade da Terra em sua órbita para cada um dos quatro meses onde os extremos são encontrados, bem como o desvio esperado da verdadeira longitude eclíptica se Bradley tivesse medido seu desvio da ascensão reta:
| Mês | Direção da velocidade tangencial da Terra no plano do colure solitário | Desvio da verdadeira declinação de γ Draconis | Direção da velocidade tangencial da Terra no plano do meridiano primo eclíptico | Desvio esperado da verdadeira longitude eclíptica de γ Draconis |
|---|---|---|---|---|
| Dezembro | zero | nenhum | ← (movimento para periélio a velocidade rápida) | diminuição de mais de 20,2" |
| Março | ← | 19.5" para o sul | zero | nenhum |
| Junho | zero | nenhum | → | aumento de menos de 20,2" |
| Setembro | → (movimento para periélio) | 19.5" para o norte | zero | nenhum |
Bradley propôs que a aberração da luz não afetava apenas a declinação, mas também a ascensão reta, de modo que uma estrela no pólo da eclíptica descreveria uma pequena elipse com um diâmetro de cerca de 40", mas para simplificar, ele presumiu que fosse um círculo. Como ele só observou o desvio em declinação, e não em ascensão reta, seus cálculos para o desvio máximo de uma estrela no pólo da eclíptica são apenas para sua declinação, que coincidirá com o diâmetro do pequeno círculo descrito por tal estrela. Para oito estrelas diferentes, seus cálculos são os seguintes:
| Estrela | Variação anual (") | Desvio máximo na declinação de uma estrela no pólo da eclíptica (") |
|---|---|---|
| γ Draconis | 39 | 40.4 |
| β Draconização | 39 | 40.2 |
| ? Ursa Maj. | 36 | 40.4 |
| Cass. | 34 | 40.8 |
| τ Persei | 25 | 41.0 |
| α Persei | 23 | 40.2 |
| 35 Camel. | 19 | 40.2 |
| Capella | 16. | 40.0 |
| MEU | 40.4 |
Com base nesses cálculos, Bradley foi capaz de estimar a constante de aberração em 20,2", que é igual a 0,00009793 radianos, e com isso foi capaz de estimar a velocidade da luz em 183.300 milhas (295.000 km) por segundo. Ao projetar o pequeno círculo para uma estrela no pólo da eclíptica, ele poderia simplificar o cálculo da relação entre a velocidade da luz e a velocidade do movimento anual da Terra em sua órbita da seguinte maneira:
- e (12D D - Sim. - Sim. 0.00009793)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =pecado (0.00009793)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =vc{displaystyle cos left({frac {1}{2}}pi -0,00009793right)=sin(0,00009793)={frac Não.
Assim, a velocidade da luz para a velocidade do movimento anual da Terra em sua órbita é de 10.210 para um, de onde seguiria, que a luz se move, ou é propagada tão longe quanto do Sol para o Terra em 8 minutos e 12 segundos.
A motivação original da busca pela paralaxe estelar era testar a teoria copernicana de que a Terra gira em torno do Sol. A mudança de aberração no curso do ano demonstra o movimento relativo da Terra e das estrelas.
Retrodição na obra de Descartes. argumento da velocidade da luz
No século anterior, René Descartes argumentou que se a luz não fosse instantânea, então as sombras dos objetos em movimento seriam atrasadas; e se os tempos de propagação em distâncias terrestres fossem apreciáveis, então, durante um eclipse lunar, o Sol, a Terra e a Lua estariam desalinhados por horas. movimento, ao contrário da observação. Huygens comentou que, com base nos dados de velocidade da luz de Rømer (produzindo um tempo de ida e volta entre a Terra e a Lua de apenas alguns segundos), o ângulo de atraso seria imperceptível. O que ambos ignoraram é que a aberração (como entendida apenas mais tarde) neutralizaria exatamente o atraso, mesmo que grande, deixando esse método de eclipse completamente insensível à velocidade da luz. (Caso contrário, os métodos de retardo de sombra poderiam ser feitos para detectar o movimento translacional absoluto, contrário ao princípio básico da relatividade.)
Teorias históricas da aberração
O fenômeno da aberração tornou-se uma força motriz para muitas teorias físicas durante os 200 anos entre sua observação e a explicação de Albert Einstein.
A primeira explicação clássica foi fornecida em 1729, por James Bradley, conforme descrito acima, que a atribuiu à velocidade finita da luz e ao movimento da Terra em sua órbita ao redor do Sol. No entanto, esta explicação provou ser imprecisa uma vez que a natureza ondulatória da luz foi melhor compreendida, e corrigi-la tornou-se um dos principais objetivos das teorias do éter luminífero do século XIX. Augustin-Jean Fresnel propôs uma correção devido ao movimento de um meio (o éter) através do qual a luz se propaga, conhecida como "arrasto parcial do éter". Ele propôs que os objetos arrastam parcialmente o éter junto com eles enquanto se movem, e essa se tornou a explicação aceita para a aberração por algum tempo. George Stokes propôs uma teoria semelhante, explicando que a aberração ocorre devido ao fluxo de éter induzido pelo movimento da Terra. Evidências acumuladas contra essas explicações, combinadas com uma nova compreensão da natureza eletromagnética da luz, levaram Hendrik Lorentz a desenvolver uma teoria do elétron que apresentava um éter imóvel, e ele explicou que os objetos se contraem em comprimento à medida que se movem através do éter. Motivado por essas teorias anteriores, Albert Einstein desenvolveu a teoria da relatividade especial em 1905, que fornece a explicação moderna da aberração.
Explicação clássica de Bradley
Bradley concebeu uma explicação em termos de uma teoria corpuscular da luz na qual a luz é feita de partículas. Sua explicação clássica apela para o movimento da Terra em relação a um feixe de partículas de luz movendo-se a uma velocidade finita e é desenvolvida no referencial do Sol, ao contrário da derivação clássica dada acima.
Considere o caso em que uma estrela distante é imóvel em relação ao Sol, e a estrela está extremamente distante, para que a paralaxe possa ser ignorada. No resto do Sol, isso significa que a luz da estrela viaja em caminhos paralelos para o observador da Terra, e chega ao mesmo ângulo, independentemente de onde a Terra está em sua órbita. Suponha que a estrela é observada na Terra com um telescópio, idealizado como um tubo estreito. A luz entra no tubo da estrela em ângulo θ θ - Sim. e viaja em velocidade cNão. tomando um tempo h/cNão. para chegar ao fundo do tubo, onde é detectado. Suponha que as observações sejam feitas da Terra, que está se movendo com uma velocidade vNão.. Durante o trânsito da luz, o tubo move uma distância vh/c- Sim.. Consequentemente, para as partículas de luz para alcançar o fundo do tubo, o tubo deve ser inclinado em um ângulo φ φ - Sim. diferente de θ θ - Sim., resultando em um aparente posição da estrela em ângulo φ φ - Sim.. À medida que a Terra prossegue em sua órbita, ela muda de direção, então φ φ - Sim. muda com o tempo do ano a observação é feita. O ângulo aparente e o ângulo verdadeiro estão relacionados usando trigonometria como:
- bronzeado (φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =hpecado (θ θ )hv/c+he (θ θ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =pecado (θ θ )v/c+e (θ θ ){displaystyle tan(phi)={frac {hsin(theta)}{hv/c+hcos(theta)}}={frac {sin(theta)}{v/c+cos(theta)}}}}}.
No caso de θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =90∘ ∘ {displaystyle theta =90^{circ), isto dá bronzeado (θ θ - Sim. - Sim. φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v/c{displaystyle tan(theta -phi)=v/c}. Embora isso seja diferente do resultado relativista mais preciso descrito acima, no limite de pequeno ângulo e baixa velocidade eles são aproximadamente os mesmos, dentro do erro das medidas do dia de Bradley. Estes resultados permitiram que Bradley fizesse uma das primeiras medidas da velocidade da luz.
Éter luminífero

No início do século XIX, a teoria ondulatória da luz estava sendo redescoberta e, em 1804, Thomas Young adaptou a explicação de Bradley para a luz corpuscular à luz ondulatória viajando através de um meio conhecido como éter luminífero. Seu raciocínio era o mesmo de Bradley, mas exigia que esse meio ficasse imóvel no referencial do Sol e passasse pela Terra sem ser afetado, caso contrário, o meio (e, portanto, a luz) se moveria junto com a terra e nenhuma aberração seria observada. Ele escreveu:
Ao considerar os fenômenos da aberração das estrelas, estou disposto a acreditar que o éter luminiferoso permeia a substância de todos os corpos materiais com pouca ou nenhuma resistência, como livremente talvez como o vento passa através de um bosque de árvores.
—Thomas Young, 1804
No entanto, logo ficou claro que a teoria de Young não poderia explicar a aberração quando os materiais com um índice não-vacuo de refração estavam presentes. Um exemplo importante é de um telescópio cheio de água. A velocidade da luz em tal telescópio será mais lenta do que no vácuo, e é dada por c/nNão. em vez de cNão. Onde? nNão. é o índice de refração da água. Assim, pelo raciocínio de Bradley e Young o ângulo de aberração é dado por
- bronzeado (φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =pecado (θ θ )v/(c/n)+e (θ θ ){displaystyle tan(phi)={frac {sin(theta)}{v/(c/n)+cos(theta)}}}.
que prevê um ângulo de aberração dependente do meio. Quando a refração na objetiva do telescópio é levada em consideração, esse resultado se desvia ainda mais do resultado do vácuo. Em 1810, François Arago realizou um experimento semelhante e descobriu que a aberração não era afetada pelo meio no telescópio, fornecendo evidências sólidas contra a teoria de Young. Esta experiência foi posteriormente verificada por muitos outros nas décadas seguintes, mais precisamente por Airy em 1871, com o mesmo resultado.
Modelos de arrasto de éter
Arrasto do éter de Fresnel
Em 1818, Augustin Fresnel desenvolveu uma explicação modificada para explicar o telescópio de água e para outros fenômenos de aberração. Ele explicou que o éter está geralmente em repouso no quadro de referência do Sol, mas os objetos parcialmente arrastam o éter junto com eles enquanto se movem. Ou seja, o éter em um objeto de índice de refração nNão. movendo-se na velocidade vNão. é parcialmente arrastado com uma velocidade (1- Sim. - Sim. 1/n2)v(I-1/n^{2})v} trazendo a luz junto com ela. Este fator é conhecido como "coeficiente de arrasto do Fresnel". Este efeito arrastando, juntamente com a refração no objetivo do telescópio, compensa a velocidade mais lenta da luz no telescópio de água na explicação de Bradley. Com esta modificação, Fresnel obteve o resultado de vácuo de Bradley mesmo para telescópios não-vacuum, e também foi capaz de prever muitos outros fenômenos relacionados à propagação da luz em corpos em movimento. O coeficiente de arrasto de Fresnel tornou-se a explicação dominante da aberração nas próximas décadas.
Stokes' arrasto do éter
No entanto, o fato de que a luz é polarizada (descoberta pelo próprio Fresnel) levou cientistas como Cauchy e Green a acreditar que o éter era um sólido elástico totalmente imóvel em oposição ao éter fluido de Fresnel. Assim, houve uma necessidade renovada de uma explicação da aberração consistente tanto com as previsões de Fresnel (e com as observações de Arago) quanto com a polarização.
Em 1845, Stokes propôs um 'tipo massa de vidraceiro' éter que atua como um líquido em grandes escalas, mas como um sólido em pequenas escalas, suportando assim as vibrações transversais necessárias para a luz polarizada e o fluxo de éter necessário para explicar a aberração. Fazendo apenas as suposições de que o fluido é irrotacional e que as condições de contorno do fluxo são tais que o éter tem velocidade zero longe da Terra, mas se move na velocidade da Terra em sua superfície e dentro dela, ele foi capaz de para explicar completamente a aberração. A velocidade do éter fora da Terra diminuiria em função da distância da Terra, de modo que os raios de luz das estrelas seriam progressivamente arrastados à medida que se aproximassem da superfície da Terra. O movimento da Terra não seria afetado pelo éter devido ao paradoxo de D'Alembert.
Tanto Fresnel quanto Stokes' teorias eram populares. No entanto, a questão da aberração foi deixada de lado durante grande parte da segunda metade do século XIX, quando o foco da investigação voltou-se para as propriedades eletromagnéticas do éter.
Lorentz' contração de comprimento
Na década de 1880, uma vez que o eletromagnetismo foi melhor compreendido, o interesse voltou-se novamente para o problema da aberração. A essa altura, as falhas eram conhecidas tanto por Fresnel quanto por Stokes. teorias. A teoria de Fresnel exigia que a velocidade relativa do éter e da matéria fosse diferente para luz de cores diferentes, e foi demonstrado que as condições de contorno que Stokes assumiu em sua teoria eram inconsistentes com sua suposição de fluxo irrotacional. Ao mesmo tempo, as teorias modernas do éter eletromagnético não poderiam explicar a aberração de forma alguma. Muitos cientistas como Maxwell, Heaviside e Hertz tentaram, sem sucesso, resolver esses problemas incorporando Fresnel ou Stokes'. teorias nas novas leis eletromagnéticas de Maxwell.
Hendrik Lorentz gastou um esforço considerável ao longo destas linhas. Depois de trabalhar neste problema por uma década, as questões com a teoria de Stokes o fizeram abandoná-lo e seguir a sugestão de Fresnel de um (principalmente) éter estacionário (1892, 1895). No entanto, no modelo de Lorentz o éter foi completamente completamente imobile, como os aethers eletromagnéticos de Cauchy, Green e Maxwell e ao contrário do éter de Fresnel. Ele obteve o coeficiente de arrasto de Fresnel a partir de modificações da teoria eletromagnética de Maxwell, incluindo uma modificação das coordenadas do tempo em quadros móveis ("hora local"). A fim de explicar a experiência Michelson-Morley (1887), que aparentemente contradiz as teorias imobilizadas de Fresnel e Lorentz, e aparentemente confirmou o arrasto completo do éter de Stokes, Lorentz teorizou (1892) que objetos passam por "contração longa" por um fator de 1- Sim. - Sim. v2/c2(1-v^{2}/c^{2}} na direção de seu movimento através do éter. Desta forma, a aberração (e todos os fenômenos ópticos relacionados) pode ser contabilizada no contexto de um éter imobilizado. A teoria de Lorentz tornou-se a base para muita pesquisa na próxima década, e além. Suas previsões para a aberração são idênticas às da teoria relativista.
Relatividade especial
Lorentz' a teoria combinava bem com a experiência, mas era complicada e fazia muitas suposições físicas infundadas sobre a natureza microscópica dos meios eletromagnéticos. Em sua teoria da relatividade especial de 1905, Albert Einstein reinterpretou os resultados de Lorentz'. teoria em uma estrutura conceitual muito mais simples e natural que dispensou a ideia de um éter. Sua derivação é dada acima, e agora é a explicação aceita. Robert S. Shankland relatou algumas conversas com Einstein, nas quais Einstein enfatizou a importância da aberração:
Ele continuou a dizer os resultados experimentais que mais o influenciaram foram as observações da aberração estelar e as medidas de Fizeau sobre a velocidade da luz na água em movimento. “Eles eram suficientes”, disse ele.
Outras motivações importantes para o desenvolvimento da relatividade de Einstein foram o problema do ímã em movimento e do condutor e (indiretamente) os experimentos de deriva do éter negativo, já mencionados por ele na introdução de seu primeiro artigo sobre a relatividade. Einstein escreveu em uma nota em 1952:
Meu próprio pensamento foi mais indiretamente influenciado pela famosa experiência Michelson-Morley. Aprendi com isso através do caminho de Lorentz quebrando a investigação sobre a eletrodinâmica dos corpos em movimento (1895), dos quais eu sabia antes do estabelecimento da teoria especial da relatividade. A suposição básica de Lorentz de um éter de repouso não me pareceu diretamente convincente, uma vez que levou a uma interpretação [forte para fora: para mim artificial aparecendo] da experiência de Michelson-Morley, que [estrela fora: não me convenceu] parecia não natural para mim. Meu caminho direto para o sp. th. rel. foi determinado principalmente pela convicção de que a força eletromotiva induzida em um condutor que se move em um campo magnético não é nada além de um campo elétrico. Mas o resultado da experiência de Fizeau e o fenômeno da aberração também me guiaram.
Enquanto o resultado de Einstein é o mesmo que a equação original de Bradley, exceto por um fator extra de γ γ - Sim., o resultado de Bradley não apenas dá o limite clássico do caso relativista, no sentido de que ele dá previsões incorretas mesmo em baixas velocidades relativas. A explicação de Bradley não pode explicar situações como o telescópio de água, nem para muitos outros efeitos ópticos (como interferência) que podem ocorrer no telescópio. Isso porque no quadro da Terra prevê que a direção da propagação do feixe de luz no telescópio não é normal para as margens do feixe, em contradição com a teoria de Maxwell do eletromagnetismo. Também não preserva a velocidade da luz c entre quadros. No entanto, Bradley inferiu corretamente que o efeito era devido a velocidades relativas.
Contenido relacionado
Antares
Konstantin Tsiolkovsky
Carina (constelação)