Vorticidad

En la mecánica de medios continuos, la vorticidad es un campo pseudovectorial que describe el movimiento giratorio local de un continuo cerca de algún punto (la tendencia de algo a girar), como lo vería un observador ubicado en ese punto. punto y viajando junto con el flujo. Es una cantidad importante en la teoría dinámica de fluidos y proporciona un marco conveniente para comprender una variedad de fenómenos de flujo complejos, como la formación y el movimiento de anillos de vórtice.

Matemáticamente, la vorticidad ⋅ ⋅ → → {displaystyle {vec {omega } es el rizo de la velocidad de flujo u→ → {displaystyle {vec}}:

⋅ ⋅ → → ↑ ↑ Silencio Silencio × × u→ → ,{displaystyle {vec {omega }equiv nabla times {vec {u},}

Donde Silencio Silencio {displaystyle nabla } es el operador de nabla. Conceptualmente, ⋅ ⋅ → → {displaystyle {vec {omega } podría determinarse marcando partes de un continuum en un pequeño barrio del punto en cuestión, y observando sus relativo desplazamientos a medida que se mueven a lo largo del flujo. La vorticidad ⋅ ⋅ → → {displaystyle {vec {omega } sería el doble de la velocidad angular media vector de esas partículas en relación con su centro de masa, orientado según la regla de la mano derecha.

En un flujo bidimensional, ⋅ ⋅ → → {displaystyle {vec {omega } es siempre perpendicular al plano del flujo, y por lo tanto se puede considerar un campo de escalar.

Ejemplos

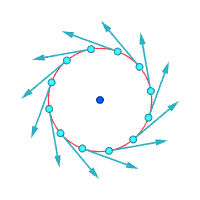
En una masa continua que gira como un cuerpo rígido, la vorticidad es el doble del vector de velocidad angular de esa rotación. Este es el caso, por ejemplo, en el núcleo central de un vórtice de Rankine.

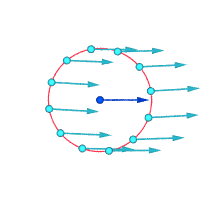
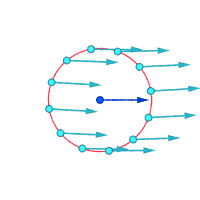
La vorticidad puede ser distinta de cero incluso cuando todas las partículas fluyen a lo largo de trayectorias rectas y paralelas, si hay cizalladura (es decir, si la velocidad del flujo varía a lo largo de las líneas de corriente). Por ejemplo, en el flujo laminar dentro de una tubería con sección transversal constante, todas las partículas viajan paralelas al eje de la tubería; pero más rápido cerca de ese eje, y prácticamente estacionario junto a las paredes. La vorticidad será cero en el eje y máxima cerca de las paredes, donde la cizalla es mayor.

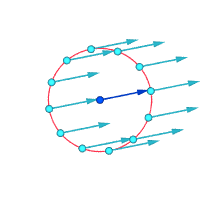
Por el contrario, un flujo puede tener vorticidad cero aunque sus partículas viajen a lo largo de trayectorias curvas. Un ejemplo es el vórtice irrotacional ideal, donde la mayoría de las partículas giran alrededor de un eje recto, con una velocidad inversamente proporcional a sus distancias a ese eje. Una pequeña parcela de continuo que no se extiende a ambos lados del eje girará en un sentido pero se cortará en el sentido opuesto, de tal manera que su velocidad angular media sobre su centro de masa sea cero.

Corrientes de ejemplo:
Rigid-body-like vortex v ∝ r	Flujo paralelo con tijera	Vortex irrestricto v ∝ 1/r
Donde v es la velocidad del flujo, r es la distancia al centro del vórtice y ∝ indica proporcionalidad. Velocidades absolutas alrededor del punto destacado:
Velocidades relativas (magnificadas) alrededor del punto destacado
Vorticidad ل 0	Vorticidad ل 0	Vorticidad = 0

Otra forma de visualizar la vorticidad es imaginar que, instantáneamente, una pequeña parte del continuo se solidifica y el resto del flujo desaparece. Si esa diminuta partícula sólida nueva está girando, en lugar de simplemente moverse con el flujo, entonces hay vorticidad en el flujo. En la siguiente figura, la subfigura izquierda no demuestra vorticidad y la subfigura derecha demuestra la existencia de vorticidad.

Definición matemática

Matemáticamente, la vorticidad de un flujo tridimensional es un campo pseudovector, generalmente denotado por ⋅ ⋅ → → {displaystyle {vec {omega }, definido como el rizo del campo de velocidad v→ → {displaystyle {vec}} describiendo la moción continua. En las coordenadas cartesianas:

⋅ ⋅ → → =Silencio Silencio × × v→ → =()∂ ∂ ∂ ∂ x∂ ∂ ∂ ∂ Sí.∂ ∂ ∂ ∂ z)× × ()vxvSí.vz)=()∂ ∂ vz∂ ∂ Sí.− − ∂ ∂ vSí.∂ ∂ z∂ ∂ vx∂ ∂ z− − ∂ ∂ vz∂ ∂ x∂ ∂ vSí.∂ ∂ x− − ∂ ∂ vx∂ ∂ Sí.).{displaystyle {begin{aligned}{vec} {omega }}=nabla times {vec {} {begin{pmatrix}{dfrac {partial }{partial x}} {dfrac {partial }{dfrac {partial }{dfrac {partial }}}}}}}} {mdfrac {fnMicrosoft Sans Serif}begin{pmatrix}v_{x} {y} {y} {v_{z}end{pmatrix}}[6px] {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}} {fnMicrosoft Sans Serif}}} {fnMicrosoft Sans Serif}}}} {\fnMicrosoft}}} {fnMicrosoft}} {fnMicrosoft}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}} { Y... {cHFF} {cHFF} {cHFF}} {cHFF}} {cHFF}} {cHFF}} {cHFF}}}} {cH}}} {cH}}}} {ccH}}}} {ccccH}}}}}}}} {cccH}}}}}}}}}}}}cccccccccccccccccccccccccccccccccccc}}}}}}}}}}}}}}ccccccccccccccccccccccccccccc {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}}} {fnMicrosoft}} {fnMicrosoft}}} {fnMicrosoft}}} {fnMicrosoft} {fnMicrosoft}}} {fnMicrosoft}}}} {f}}}}}}}}}}}}}}}}}}}}}}} {\b}}}} {b} {b}}}}}} {b} {b}}}}}}}}} {b}}}}}}}}}}}}}}} {b}}}}}}}}}}}}}}}}\\\\\\b} {b}}}}}}}}}}}}b}}}}}}}}}}}}}}}}}}}}}}}} z}-{dfrac {cHFF} {cHFF} {cHFF}} {cHFF}} {cHFF}}} {cc}}} {cc}}}}}}ccccccH}}} {cccH}}}} {ccH}}}}}}ccccccc}}}}}}}}}}}}cccccccccccccccccccccc}}}}}}}}}}}}cccccccccccccccccccc}}}}}}}}}}}}}}}}}}}}}cccccccccc {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}}} {fnMicrosoft}}} {f}}}} {fnMicrosoft}}}}}} {\fnMicrosoft}}} {fnMicrosoft}}}}}}}}}}}} {\\\\\\\\\cH}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {b}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\ccb}}}}}}}}}}}} {fnMicroc {fnK} {fnMicrosoft}fnMicrosoft Sans Serif}},end{aligned}}}}

En palabras, la vorticidad indica cómo cambia el vector de velocidad cuando uno se mueve una distancia infinitesimal en una dirección perpendicular a él.

En un flujo bidimensional donde la velocidad es independiente de z{displaystyle z}-coordinado y no tiene z{displaystyle z}-componente, el vector de vorticidad siempre es paralelo al z{displaystyle z}-eje, y por lo tanto se puede expresar como un campo escalar multiplicado por una unidad constante vectorial z^ ^ {displaystyle {hat {z}}}:

⋅ ⋅ → → =Silencio Silencio × × v→ → =()∂ ∂ ∂ ∂ x∂ ∂ ∂ ∂ Sí.∂ ∂ ∂ ∂ z)× × ()vxvSí.vz)=()∂ ∂ vSí.∂ ∂ x− − ∂ ∂ vx∂ ∂ Sí.)z^ ^ .{displaystyle {begin{aligned}{vec} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {c} {fnMicros} {fnMicros} {fnMicrosoft} {fnMicrosoft} {fnMicros} {fnMicrosoft} {fnMicrosoft} {f} {f} {f}f}fnMicros}fnMicros}f}f}f}f}fnMicros}f}f}fnMicrosoft}fnMis}fnMis}f}fnMicros}fnMis}fnMis}fnun}fnun}f}fnun}fnMiss}fnMinun}fnMinMinMinMis}fnMinMicrosoft}fnunci} {fnMin {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}} {fnMicrosoft}}} {fnMicrosoft}}} {fnMicrosoft}}} {fnMicrosoft}}}} {fnMicrosoft}}}}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}} { {fnMicroc {fnMicroc} {fnMicrosoft Sans Serif}fnMicrosoft Sans Serif}} {fnunció}

La vorticidad también está relacionada con la circulación del flujo (línea integral de la velocidad) a lo largo de un camino cerrado por el teorema (clásico) de Stokes. Es decir, para cualquier elemento superficial infinitesimal C con dirección normal n→ → {displaystyle {vec}} y zona dA{displaystyle dA}, la circulación d.. {displaystyle dGamma } a lo largo del perímetro C{displaystyle C} es el producto de punto ⋅ ⋅ → → ⋅ ⋅ ()n→ → dA){displaystyle {vec {omega }cdot ({vec { n},dA)} Donde ⋅ ⋅ → → {displaystyle {vec {omega } es la vorticidad en el centro de C{displaystyle C}.

Evolución

La evolución del campo de vorticidad en el tiempo se describe mediante la ecuación de vorticidad, que puede derivarse de las ecuaciones de Navier-Stokes.

En muchos flujos reales en los que se puede despreciar la viscosidad (más precisamente, en flujos con un número de Reynolds alto), el campo de vorticidad se puede modelar mediante una colección de vórtices discretos, siendo la vorticidad despreciable en todas partes excepto en pequeñas regiones del espacio que rodea los ejes de los vórtices. Esto es cierto en el caso del flujo potencial bidimensional (es decir, flujo de viscosidad cero bidimensional), en cuyo caso el campo de flujo se puede modelar como un campo de valores complejos en el plano complejo.

La vorticidad es útil para comprender cómo se pueden perturbar las soluciones ideales de flujo potencial para modelar flujos reales. En general, la presencia de viscosidad provoca una difusión de vorticidad desde los núcleos de vórtice hacia el campo de flujo general; este flujo se explica por un término de difusión en la ecuación de transporte de vorticidad.

Líneas de vórtice y tubos de vórtice

Una línea de vórtice o línea de vorticidad es una línea que es tangente en todas partes al vector de vorticidad local. Las líneas de vórtice están definidas por la relación

dx⋅ ⋅ x=dSí.⋅ ⋅ Sí.=dz⋅ ⋅ z,{displaystyle {frac {dx}{omega ¿Qué? {y}{omega ¿Qué? {dz}{omega.

Donde ⋅ ⋅ → → =()⋅ ⋅ x,⋅ ⋅ Sí.,⋅ ⋅ z){displaystyle {vec {omega}=(omega _{x},omega _{y},omega _{z}}} es el vector de vorticidad en coordenadas cartesianas.

Un tubo de vórtice es la superficie en el continuo formada por todas las líneas de vórtice que pasan a través de una curva cerrada dada (reducible) en el continuo. La 'fuerza' de un tubo de vórtice (también llamado flujo de vórtice) es la integral de la vorticidad en una sección transversal del tubo, y es la misma en todas partes a lo largo del tubo (porque la vorticidad tiene divergencia cero). Es una consecuencia de los teoremas de Helmholtz (o equivalentemente, del teorema de circulación de Kelvin) que en un fluido no viscoso la 'fuerza'; del tubo de vórtice también es constante con el tiempo. Los efectos viscosos introducen pérdidas por fricción y dependencia del tiempo.

En un flujo tridimensional, la vorticidad (medida por la integral de volumen del cuadrado de su magnitud) puede intensificarse cuando se extiende una línea de vórtice, un fenómeno conocido como estiramiento de vórtice. Este fenómeno ocurre en la formación de un vórtice de bañera en el agua que sale y la acumulación de un tornado por corrientes de aire ascendentes.

Medidores de vorticidad

Medidor de vorticidad de paleta giratoria

El ingeniero hidráulico ruso A. Ya inventó un medidor de vorticidad de paleta giratoria. Milovich (1874-1958). En 1913 propuso un corcho con cuatro aspas unidas como dispositivo que mostraba cualitativamente la magnitud de la proyección vertical de la vorticidad y demostró una fotografía cinematográfica del movimiento del flotador en la superficie del agua en un modelo de un recodo del río..

Los medidores de vorticidad de paletas giratorias se muestran comúnmente en películas educativas sobre mecánica continua (ejemplos famosos incluyen 'Vorticidad' del NCFMF y 'Principios fundamentales del flujo' del Instituto de Iowa de Investigaciones Hidráulicas).

Ciencias específicas

Aeronáutica

En aerodinámica, la distribución de sustentación sobre un ala finita se puede aproximar suponiendo que cada segmento del ala tiene un vórtice de cola semi-infinito detrás de él. Entonces es posible resolver la fuerza de los vórtices utilizando el criterio de que no haya flujo inducido a través de la superficie del ala. Este procedimiento se denomina método de panel de vórtice de dinámica de fluidos computacional. Luego se suman las fuerzas de los vórtices para encontrar la circulación total aproximada alrededor del ala. Según el teorema de Kutta-Joukowski, la sustentación es el producto de la circulación, la velocidad del aire y la densidad del aire.

Ciencias atmosféricas

La vorticidad relativa es la vorticidad relativa a la Tierra inducida por el campo de velocidad del aire. Este campo de velocidad del aire a menudo se modela como un flujo bidimensional paralelo al suelo, de modo que el vector de vorticidad relativa es generalmente una cantidad escalar de rotación perpendicular al suelo. La vorticidad es positiva cuando, mirando hacia la superficie terrestre, el viento gira en sentido contrario a las agujas del reloj. En el hemisferio norte, la vorticidad positiva se llama rotación ciclónica y la vorticidad negativa es rotación anticiclónica; la nomenclatura se invierte en el hemisferio sur.

La vorticidad absoluta se calcula a partir de la velocidad del aire relativa a un marco inercial y, por lo tanto, incluye un término debido a la rotación de la Tierra, el parámetro de Coriolis.

La vorticidad potencial es la vorticidad absoluta dividida por el espacio vertical entre los niveles de temperatura (o entropía) constante (potencial). La vorticidad absoluta de una masa de aire cambiará si la masa de aire se estira (o comprime) en dirección vertical, pero la vorticidad potencial se conserva en un flujo adiabático. Dado que el flujo adiabático predomina en la atmósfera, la vorticidad potencial es útil como indicador aproximado de las masas de aire en la atmósfera en la escala de tiempo de unos pocos días, particularmente cuando se observa en niveles de entropía constante.

La ecuación de vorticidad barotrópica es la forma más sencilla de pronosticar el movimiento de las ondas de Rossby (es decir, las vaguadas y crestas de 500 hPa de altura geopotencial) durante un período de tiempo limitado (unos pocos días). En la década de 1950, los primeros programas exitosos de pronóstico numérico del tiempo utilizaron esa ecuación.

En los modelos numéricos de pronóstico del tiempo y los modelos de circulación general (GCM) modernos, la vorticidad puede ser una de las variables predichas, en cuyo caso la ecuación dependiente del tiempo correspondiente es una ecuación de pronóstico.

Relacionado con el concepto de vorticidad es la helicidad H()t){displaystyle H(t)}, definido como

H()t)=∫ ∫ Vu→ → ⋅ ⋅ ⋅ ⋅ → → dV{displaystyle H(t)=int ¿Qué?

donde la integral está sobre un volumen dado V{displaystyle V}. En la ciencia atmosférica, la helicidad del movimiento aéreo es importante en la predicción de las supercells y el potencial para la actividad tornadica.