Volumen

Compartir Imprimir Citar

Volumen es la cantidad de espacio que ocupa la materia.

O en otras palabras, el volumen representa la extensión longitudinal de una región del espacio en todas sus direcciones (tridimensionalmente). Todos los cuerpos físicos, bien sean sólidos, líquidos, gaseosos o plasma, poseen volumen, pues existen dentro de las tres dimensiones espaciales.

El volumen a menudo se cuantifica numéricamente utilizando la unidad derivada del sistema internacional: el metro cúbico. El volumen de un contenedor se entiende generalmente como la capacidad del contenedor; es decir, la cantidad de fluido (gas o líquido) que podría contener el recipiente, en lugar de la cantidad de espacio que desplaza el propio recipiente. A las formas matemáticas tridimensionales también se les asignan volúmenes. Los volúmenes de algunas formas simples, como las formas regulares, de bordes rectos y circulares, se pueden calcular fácilmente usando fórmulas aritméticas. Los volúmenes de formas complicadas se pueden calcular con cálculo integral si existe una fórmula para el límite de la forma. A las figuras unidimensionales (como las líneas) y las formas bidimensionales (como los cuadrados) se les asigna un volumen cero en el espacio tridimensional.

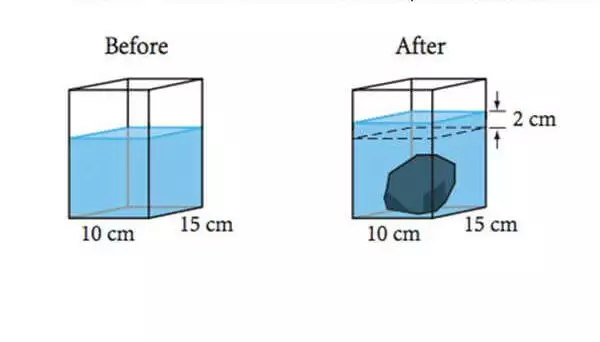
El volumen de un sólido (ya sea de forma regular o irregular) se puede determinar mediante el desplazamiento de un fluido. El desplazamiento de líquido también se puede utilizar para determinar el volumen de un gas. El volumen combinado de dos sustancias suele ser mayor que el volumen de una sola de las sustancias. Sin embargo, a veces una sustancia se disuelve en la otra y en tales casos el volumen combinado no es aditivo.

Experimento de la piedra en un recipiente para calcular su volumen

Unidades

En geometría diferencial, el volumen se expresa por medio de la forma de volumen y es un invariante de Riemann global importante. En termodinámica, el volumen es un parámetro fundamental, y es una variable conjugada a la presión.

Cualquier unidad de longitud da una unidad de volumen correspondiente: el volumen de un cubo cuyos lados tienen la longitud dada. Por ejemplo, un centímetro cúbico (cm) es el volumen de un cubo cuyos lados miden un centímetro (1 cm) de longitud.

En el Sistema Internacional de Unidades (SI), la unidad estándar de volumen es el metro cúbico (m). El sistema métrico también incluye el litro (L) como unidad de volumen, donde un litro es el volumen de un cubo de 10 centímetros. Por lo tanto1 = (10 cm) = 1000 centímetros cúbicos = 0,001 metros cúbicos,

entonces1 metro cúbico = 1000 litros.

Las pequeñas cantidades de líquido a menudo se miden en mililitros, donde1 mililitro = 0,001 litros = 1 centímetro cúbico.

De la misma manera, grandes cantidades se pueden medir en megalitros, donde1 millón de litros = 1000 metros cúbicos = 1 megalitro.

También se utilizan otras unidades tradicionales de volumen, como la pulgada cúbica, el pie cúbico, la yarda cúbica, la milla cúbica, la cucharadita, la cucharada, la onza líquida, el dram líquido, la branquia, la pinta, el cuarto, el galón, el mínimo, el barril, la cuerda, el peck, el bushel, el tonel, el acre-pie y el pie tabla. Todas estas son unidades de volumen.

Términos relacionados

El Oxford English Dictionary define la capacidad como "la medida aplicada al contenido de un recipiente, y a los líquidos, granos o similares, que toman la forma de aquello que los contiene". (La palabra capacidadtiene otros significados no relacionados, como por ejemplo, gestión de capacidad.) Capacidad no tiene un significado idéntico al de volumen, aunque está estrechamente relacionado; la capacidad de un recipiente es siempre el volumen en su interior. Las unidades de capacidad son el SI litro y sus unidades derivadas, y las unidades imperiales como gill, pinta, galón y otras. Las unidades de volumen son los cubos de las unidades de longitud. En el SI las unidades de volumen y capacidad están íntimamente relacionadas: un litro es exactamente 1 decímetro cúbico, la capacidad de un cubo de 10 cm de lado. En otros sistemas la conversión no es trivial; la capacidad del tanque de combustible de un vehículo rara vez se expresa en pies cúbicos, por ejemplo, sino en galones (un galón imperial llena un volumen de 0,1605 pies cúbicos).

La densidad de un objeto se define como la relación entre la masa y el volumen. El inverso de la densidad es el volumen específico, que se define como el volumen dividido por la masa. El volumen específico es un concepto importante en termodinámica donde el volumen de un fluido de trabajo es a menudo un parámetro importante de un sistema que se estudia.

El caudal volumétrico en dinámica de fluidos es el volumen de fluido que pasa a través de una superficie determinada por unidad de tiempo (por ejemplo, metros cúbicos por segundo [m s ]).

El espacio volumétrico es una región 3D que tiene una forma además de capacidad o volumen.

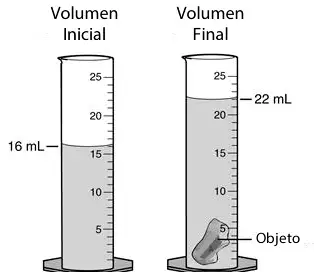
Experimento para calcular el volumen

Dado que dos objetos no pueden ocupar el mismo espacio al sumergir una roca en un recipiente que contiene agua permite medir el volumen que ocupa la piedra al medir el volumen de líquido que se desplaza.

Relaciones de volúmenes de un cono, esfera y cilindro del mismo radio y altura

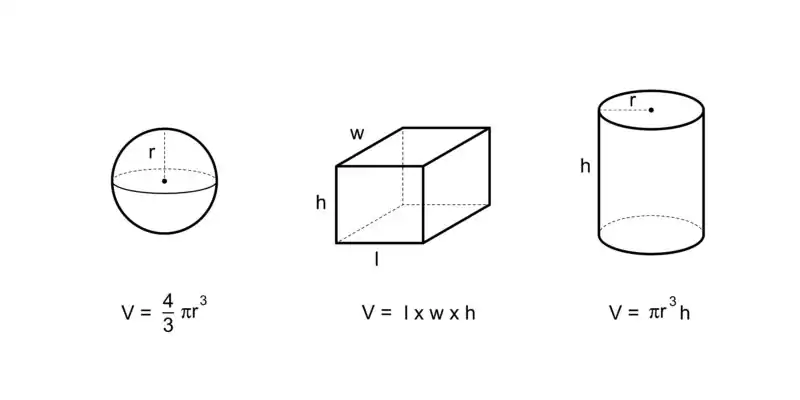
Las fórmulas anteriores se pueden usar para mostrar que los volúmenes de un cono, esfera y cilindro del mismo radio y altura están en la proporción 1: 2: 3, de la siguiente manera.

Sea el radio r y la altura h (que es 2 r para la esfera), entonces el volumen del cono es ${displaystyle {frac {1}{3}}pi r^{2}h={frac {1}{3}}pi r^{2}left(2rright)=left({frac{2}{3}}pi r^{3}right)times 1,}$ el volumen de la esfera es ${displaystyle {frac {4}{3}}pi r^{3}=left({frac {2}{3}}pi r^{3}right)times 2,}$ mientras que el volumen del cilindro es ${displaystyle pi r^{2}h=pi r^{2}(2r)=left({frac {2}{3}}pi r^{3}right)times 3. }$

El descubrimiento de la relación 2:3 de los volúmenes de la esfera y el cilindro se atribuye a Arquímedes.

El cono es un tipo de forma piramidal. La ecuación fundamental de las pirámides, un tercio de la base por la altura, también se aplica a los conos.

Sin embargo, usando el cálculo, el volumen de un cono es la integral de un número infinito de discos circulares infinitesimalmente delgados de espesor dx. El cálculo del volumen de un cono de altura h, cuya base está centrada en (0, 0, 0) con radio r, es el siguiente.

Geometría diferencial

En geometría diferencial, una rama de las matemáticas, una forma de volumen en una variedad diferenciable es una forma diferencial de grado superior (es decir, cuyo grado es igual a la dimensión de la variedad) que en ninguna parte es igual a cero. Una variedad tiene forma de volumen si y solo si es orientable. Una variedad orientable tiene infinitas formas de volumen, ya que al multiplicar una forma de volumen por una función que no se anula se obtiene otra forma de volumen. En variedades no orientables, se puede definir la noción más débil de densidad. La integración de la forma del volumen da el volumen de la variedad según esa forma.

Una variedad pseudo-Riemanniana orientada tiene una forma de volumen natural. En coordenadas locales, se puede expresar como ${displaystyle omega ={sqrt {|g|}},dx^{1}cuña puntos cuña dx^{n},}$ donde el $dx^{i}$ son formas 1 que forman una base orientada positivamente para el paquete cotangente de la variedad, y $gramo$ es el determinante de la representación matricial del tensor métrico en la variedad en términos de la misma base.

Termodinámica

En termodinámica, el volumen de un sistema es un parámetro extensivo importante para describir su estado termodinámico. El volumen específico, una propiedad intensiva, es el volumen del sistema por unidad de masa. El volumen es una función de estado y es interdependiente con otras propiedades termodinámicas como la presión y la temperatura. Por ejemplo, el volumen está relacionado con la presión y la temperatura de un gas ideal por la ley de los gases ideales.

Cálculo

La tarea de calcular numéricamente el volumen de objetos se estudia en el campo de la geometría computacional en informática, investigando algoritmos eficientes para realizar este cálculo, de forma aproximada o exacta, para diversos tipos de objetos. Por ejemplo, la técnica de aproximación del volumen convexo muestra cómo aproximar el volumen de cualquier cuerpo convexo usando un oráculo de membresía.

Fórmulas par hallar el volumen

El cálculo del volumen depende de la figura geométrica sobre la cual se quiera calcular, porque dada la cantidad mínima de variables (3) esta puede tomar muchas formas. En cálculo el volumen de una región D en R viene dado por una integral triple de la función constante $f(x,y,z)=1$ , pero en cada caso es diferente su aplicación.

Forma	Fórmula de volumen	Variables
Cubo	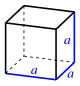$un^{3}$
Cuboides	$a B C$
Prisma(B: área de la base)	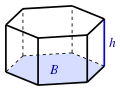${ estilo de visualización Bh}$
Pirámide(B: área de la base)	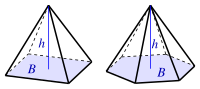${frac{1}{3}}Bh$
Paralelepípedo	${displaystyle abc{sqrt {K}}}$ ${displaystyle {begin{alineado}K=1&+2cos(alpha)cos(beta)cos(gamma)\&-cos ^{2}(alpha)-cos ^ {2}(beta)-cos ^{2}(gamma)end{alineado}}}$
tetraedro regular	${{sqrt {2}} sobre 12}a^{3},$
Esfera	${displaystyle {frac{4}{3}}pi r^{3}}$
Concha esférica	${displaystyle {frac {4}{3}}pi (R^{3}-r^{3})}$
elipsoide	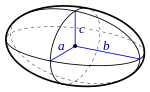${displaystyle {frac{4}{3}}pi abc}$
Cilindro circular	${ estilo de visualización pi r ^ {2} h}$
Cono	${displaystyle {frac{1}{3}}pi r^{2}h}$
Toro sólido	${ estilo de visualización 2 pi ^ {2} Rr ^ {2}}$
Sólido de revolución	${displaystyle pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x}$
Cuerpo sólido con área continua $Hacha)$ de sus secciones transversales(ejemplo: Steinmetz sólido)	${displaystyle int _{a}^{ b}A(x)mathrm {d} x}$	Para el sólido de revolución anterior: ${displaystyle A(x)=pi f(x)^{2}}$