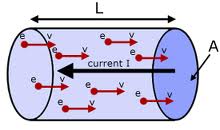
Velocidad de deriva

En física, la velocidad de deriva es la velocidad media que alcanzan las partículas cargadas, como los electrones, en un material debido a un campo eléctrico. En general, un electrón en un conductor se propagará aleatoriamente a la velocidad de Fermi, lo que dará como resultado una velocidad promedio de cero. La aplicación de un campo eléctrico añade a este movimiento aleatorio un pequeño flujo neto en una dirección; esta es la deriva.

Velocidad de derivación de electrones

La velocidad de deriva es proporcional a la corriente. En un material resistivo, también es proporcional a la magnitud de un campo eléctrico externo. Por lo tanto, la ley de Ohm se puede explicar en términos de velocidad de deriva. La expresión más elemental de la ley es:

u=μ μ E,{displaystyle u=mu E,}

donde u es la velocidad de deriva, μ es la la movilidad de electrones del material, y E es el campo eléctrico. En el sistema MKS, la velocidad de deriva tiene unidades de m/s, movilidad de electrones, m²/(V·s) y campo eléctrico, V/m.

Cuando se aplica una diferencia de potencial a través de un conductor, los electrones libres ganan velocidad en la dirección opuesta al campo eléctrico entre colisiones sucesivas (y pierden velocidad cuando viajan en la dirección del campo), adquiriendo así un componente de velocidad en ese dirección además de su velocidad térmica aleatoria. Como resultado, existe una pequeña velocidad definida de deriva de los electrones, que se superpone al movimiento aleatorio de los electrones libres. Debido a esta velocidad de deriva, existe un flujo neto de electrones opuesto a la dirección del campo.

Medida experimental

La fórmula para evaluar la velocidad de deriva de los portadores de carga en un material de área de sección transversal constante viene dada por:

u=jnq,{displaystyle u={j over nq}

donde u es la velocidad de deriva de los electrones, j es la densidad de corriente que fluye a través del material, n es la densidad numérica del portador de carga y q es la carga en el portador de carga.

Esto también se puede escribir como:

j=nqu{displaystyle j=nqu}

Pero la densidad de corriente y la velocidad de deriva, j y u, son en realidad vectores, por lo que esta relación suele escribirse como:

J=*** *** u{displaystyle mathbf {J} =rho mathbf {u} ,}

dónde

*** *** =nq{displaystyle rho =nq}

es la densidad de carga (unidad SI: culombios por metro cúbico).

En términos de las propiedades básicas del conductor óhmico metálico portador de corriente cilíndrico recto, donde los portadores de carga son electrones, esta expresión se puede reescribir como:

u=mσ σ Δ Δ V*** *** efl l ,{displaystyle u={m;sigma Delta V over rho efell },}

dónde

• u es otra vez la velocidad de deriva de los electrones, en m⋅s⁻¹
• m es la masa molecular del metal, en kg
• σ es la conductividad eléctrica del medio a la temperatura considerada, en S/m.
• ΔV es el voltaje aplicado a través del conductor, en V
• *** es la densidad (masa por volumen de unidad) del conductor, en kg⋅m⁻³
• e es la carga primaria, en C
• f es el número de electrones libres por átomo
• l es la longitud del conductor, en m

Ejemplo numérico

La electricidad se conduce más comúnmente a través de cables de cobre. El cobre tiene una densidad de 8,94 g/cm³ y un peso atómico de 63,546 g/mol, por lo que hay 140685.5 mol/m³. En un mol de cualquier elemento, hay 6.022×10²³ átomos (el número de Avogadro). Por lo tanto, en 1 m³ de cobre, hay aproximadamente 8.5× 10²⁸ átomos (6,022×10²³ × 140685.5 mol/m³). El cobre tiene un electrón libre por átomo, por lo que n es igual a 8.5×10²⁸ electrones por cúbico metro.

Supongamos una corriente I = 1 amperio y un cable de 2 mm diámetro (radio = 0,001 m). Este cable tiene un área de sección transversal A de π × (0,001 m)² = 3,14×10⁻⁶ m² = 3,14 mm². La carga de un electrón es q = −1.6×10⁻¹⁹ C. Por lo tanto, la velocidad de deriva se puede calcular:

u=InAq=1C/s()8,5× × 1028m− − 3)()3.14× × 10− − 6m2)()1.6× × 10− − 19C)=2.3× × 10− − 5m/s{displaystyle {begin{aligned}u ventaja={I over nAq}\\frac {1{text{C}/{text{s}}}{left(8.5times 10^{28}{text{m}}{-3}right)left(3.14times 10^{-6}{m} {2}right)left(1.6times ¿Qué?

Análisis dimensional:

u=Aelectronesm3⋅ ⋅ m2⋅ ⋅ Celectrones=Cs1m⋅ ⋅ C=ms{displaystyle u={dfrac {text{A}{dfrac {text{electron}{text{m}} {cdot}} {cdot}} {cdot}}} {cdot}}}}} {cdot}}} {cdot}} {cdot}} {cdot}} {cdot}}} {cdot}} {cdot}} {c}}}}} {cdot}}}} {cdot} {cdot} {c} {cdot}}}}}}} {cdot} {c} {c}} {c}}} {c}}}} {c}}} {cdot} {cdot}} {cdot}}} {cdot} {cdot} {c}} {c}} {cdot}} {cdot} {c}}}}}}}} {cdot} {c}}}} } {text{m}}}={dfrac {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}}} {fnMicroc}}}} {fnMicroc}}} {fnMicroc} {fnMicroc}}} {f}}}}} {f}}} {f}}}} {f}}}} {f}} {f}}}} {f}} {f}}}}} {f} {f} {f}}}} {f}}}}}}}}}}}}}}}}}} {f} {f}}}} {f}}} {f}}}} {f}}}}}f}f}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}} {1}{m} {cdot} {cdot}} {cdot}} {cdot}}} {cdot}}} {cdot}}} {cdot}} {cdot}} {cdot}} {cdot} {cdot} {cdot} {cdot}} {c} {c} {cdot}} {cdot} {cdot} {cdot} {c} {cdot} {c} {cdot} {c} {c} {c}}}} {c} {c} {cdot} {c} {cdot} {cdot} {cdot} {c} {cdot} {cdot} {c} {c} {cdot} {cdot} {c} {c} {c} {c} {c} {fnK}} {fnK}}} {fnK}}}} {fnK}}}}} {fn}}}}} {fn}}}}} {fnfnK}}}}}}} {f}}}}} {f}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Por lo tanto, en este cable, los electrones fluyen a una velocidad de 23 μm/s. A 60 Hz de corriente alterna, esto significa que, en medio ciclo, en promedio, los electrones se desplazan menos de 0,2 μm. En contexto, en un amperio alrededor de 3×10¹⁶ electrones fluirán a través del punto de contacto dos veces por ciclo. Pero fuera de 1×10²² electrones móviles por metro de cable, esta es una fracción insignificante.

En comparación, la velocidad de flujo de Fermi de estos electrones (que, a temperatura ambiente, se puede considerar como su velocidad aproximada en ausencia de corriente eléctrica) es de alrededor de 1570 km/s.