Vela magnética

Una vela magnética es un método propuesto de propulsión de naves espaciales que utiliza un campo magnético estático para desviar un viento de plasma de partículas cargadas radiadas por el Sol o una estrella, transfiriendo así impulso para acelerar o desacelerar una nave espacial.. La mayoría de los enfoques requieren poco o ningún propulsor y, por lo tanto, son una forma de propulsión de campo. Una vela magnética también podría empujar contra una ionosfera o magnetosfera planetaria. Los casos de uso importantes son: una fuerza modesta del viento solar sostenible durante un largo período de tiempo; desaceleración en el medio interestelar y el viento de plasma de una estrella de destino después del viaje interestelar a velocidades relativistas logradas por algún otro medio; y desaceleración eficiente en una ionosfera planetaria. Las características del plasma para el viento solar, una ionosfera planetaria y el medio interestelar y los detalles del diseño de la vela magnética determinan el rendimiento alcanzable; tales como empuje, potencia requerida y masa.

Historia del concepto

Dana Andrews y Robert Zubrin propusieron por primera vez el concepto de vela magnética en 1988. Andrews estaba trabajando en el uso de una pala magnética para recolectar material interestelar como propulsor para una nave espacial de propulsión de iones eléctricos nucleares, lo que permitía que la nave operara de manera similar a un estatorreactor Bussard. Andrews le pidió a Zubrin que lo ayudara a calcular el arrastre de la cuchara magnética contra el medio interplanetario, que resultó ser mucho mayor que el empuje de la impulsión de iones. Se eliminó el componente de impulsión de iones del sistema y nació el uso del concepto de usar la pala magnética como una vela magnética o Magsail (MS). El análisis de magsail publicado se realizó para interestelar en 1988, interplanetario en 1989, propulsión orbital planetaria en 1991 y un diseño detallado en 2000. Freeland realizó un análisis adicional en 2015 para el Proyecto Icarus que utilizó un modelo más preciso del campo magnético y mostró que Andrews y los resultados de Zubrin para la resistencia (empuje) fueron optimistas por un factor de 3,1. En 2016, Gros publicó los resultados del uso de magsail para la desaceleración en el medio interestelar. En 2017, Crowl documentó un análisis para una misión que comenzaba cerca del Sol y tenía como destino el Planeta nueve. Otro perfil de misión para la vela magnética son las transferencias heliocéntricas, como se describe en 2013 por Quarta, en 2019 por Bassetto y en 2020 por Perakis.

Un inconveniente del diseño de las velas fue que se requería un gran bucle superconductor (50–100 km) que pesaba sobre el orden de 100 toneladas (100,000 kg). En 2000, Winglee propuso un Mini-Magnetosférico Plasma Propulsión (M2P2) diseño que inyecta plasma de baja energía en una bobina mucho más pequeña con masa mucho menor que requiere baja potencia. Las simulaciones predijeron un rendimiento impresionante en relación con la masa y el poder requerido, siendo un factor importante un reclamado ${displaystyle 1/r}$ tasa de caída del campo magnético en comparación con el clásico ${textstyle 1/r^{3}$ tasa de caída de un dipolo magnético en un vacío. Una serie de críticas plantearon problemas: que la tasa de caída del campo magnético asumida era optimista y que el empuje también se sobreestimaba, un análisis que indicaba que el empuje predicho era más de diez órdenes de magnitud optimista, ya que la mayoría del impulso del viento solar se entregó al magnetotail y las fugas actuales a través de la magnetopausia y no a la nave espacial, y que la conservación del flujo magnético en la región fuera de la magnetosfera no se consideró.

A partir de 2003, Funaki y otros publicaron una serie de investigaciones teóricas, de simulación y experimentales en JAXA en colaboración con universidades japonesas que abordaron algunos de los problemas de las críticas a M2P2 y llamaron a su enfoque MagnetoPlasma Sail (MPS). En 2011, Funaki y Yamakawa escribieron un capítulo en un libro que es una buena referencia para la teoría y los conceptos de las velas magnéticas. La investigación de MPS dio como resultado muchos artículos publicados que avanzaron en la comprensión de los principios físicos de las velas magnéticas. Los resultados publicados en 2013 por Funaki y otros encontraron que el mejor rendimiento se producía cuando el plasma inyectado tenía una densidad y una velocidad más bajas que las consideradas en M2P2, donde la deriva de iones creaba una corriente de anillo ecuatorial que aumentaba el momento magnético de la bobina, cuyas simulaciones indicaron que lograron un empuje. ganancia del orden de 10 para magnetosferas más pequeñas en comparación con una vela magnética modelada por MHD. Las investigaciones continuaron informando un aumento del empuje experimental y numéricamente considerando el uso de un propulsor magnetoplasmadinámico (también conocido como chorro de arco MPD en Japón), múltiples bobinas de antena y un propulsor MPD multipolar.

John Slough de la Universidad de Washington documentó en 2004 y 2006 los resultados de la investigación, el desarrollo y la experimentación financiados por el Instituto de Conceptos Avanzados (NIAC) de la NASA para un método más eficiente para generar el dipolo magnético estático para una vela magnética usando un diseño llamado el imán de plasma (PM). El diseño usó un par de pequeñas bobinas orientadas perpendicularmente alimentadas por una corriente alterna para generar un campo magnético giratorio (RMF) que opera a una frecuencia demasiado rápida para que reaccionen los iones cargados positivamente, pero lo suficientemente lenta como para forzar a los electrones a co-rotar con el RMF sin creando colisiones excesivas. Este sistema creó un gran disco de corriente compuesto por electrones capturados del viento de plasma dentro de un disco estático de iones positivos capturados. Los informes predijeron mejoras sustanciales en términos de tamaño de bobina reducido (y, por lo tanto, masa) y requisitos de potencia notablemente más bajos para un empuje significativo. Un factor importante en estas predicciones fue una tasa hipotética de caída del campo magnético de 1/r como se supuso para M2P2. En 2022, una prueba de vuelo espacial denominada Experimento de velocidad de observación de Júpiter (JOVE) propuso usar una vela basada en un imán de plasma para una nave espacial llamada Wind Rider que usa el viento solar para acelerar lejos de un punto cercano a la Tierra y desacelerar contra la magnetosfera de Júpiter.

Un estudio de 2012 realizado por Kirtley y Slough investigó el uso de la tecnología de imanes de plasma para usar el plasma en la ionosfera de un planeta como mecanismo de frenado y se denominó Plasma Magnetoshell. Este documento reafirmó la tasa de caída del campo magnético para un imán de plasma como 1/r². Kelly y Little en 2019 y 2021 publicaron resultados de simulación que muestran que el magnetoshell era más eficiente que el frenado Aerocapture para la inserción orbital alrededor de Neptuno.

En 2021, Zhenyu Yang y otros publicaron un análisis, cálculos numéricos y verificación experimental de un sistema de propulsión que era una combinación de la vela magnética y la vela eléctrica denominada vela electromagnética. Una bobina de vela magnética superconductora aumentada por un cañón de electrones en el centro de la bobina genera un campo eléctrico como en una vela eléctrica que desvía los iones positivos en el viento de plasma proporcionando así un empuje adicional, lo que podría reducir la masa general del sistema.

Modos de funcionamiento

Los modos de navegación magnéticos de operación cubren el perfil de la misión y el medio ambiente generalmente implicando plasma como el viento solar, una ionosfera planetaria o el medio interestelar. Un entorno de plasma tiene parámetros fundamentales del número de iones de tipo ${displaystyle i}$ (con número atómico ${displaystyle Z_{i}$) en un volumen de unidad ${displaystyle No.$, la masa promedio de cada tipo de iones contable para isótopos ${displaystyle #$ (kg) y el número de electrones por volumen de unidad ${displaystyle n_{e}$ cada uno con masa de electrones ${displaystyle m_{e}$ (kg). Un plasma es de significado cuasi neutro que en promedio no hay carga eléctrica, es decir, ${displaystyle n_{e}=textstyle sum ¿Qué?$. Densidad promedio de masa por volumen de unidad de un ambiente de plasma ${displaystyle pe}$ ()${displaystyle sw}$ para el viento estelar, ${displaystyle pi}$ para la ionosfera planetaria, ${displaystyle im}$ para el medio interestelar) es ${displaystyle textstyle rho ### {fn}m_{e}+sum ¿Qué?$ (kg/m³). La distribución de velocidad de iones y electrones es otro parámetro importante pero a menudo los análisis utilizan sólo la velocidad promedio para un viento de plasma ${displaystyle v_{pe}$ (m/s).

Aceleración/desaceleración en un viento de plasma estelar

Un caso de uso de vela magnética comúnmente encontrado está creando arrastre contra un viento de plasma de una estrella cercana que acelera una nave espacial lejos de la estrella. Muchos diseños, análisis, simulaciones y experimentos se centran en este caso de uso. El viento solar es un flujo de plasma que varía en el tiempo que fluye hacia fuera del Sol. Cerca de la órbita de la Tierra a 1 Unidad Astronómica (AU) el plasma fluye a velocidad ${displaystyle v_{sw}$ de 250 a 750 km/s (155-404 mi/s) con una densidad que oscila entre 3 y 10 electrones, protones y partículas alfa por cm³ junto con algunos iones más pesados por centímetro cúbico. Asumiendo que el 8% del viento solar es helio y el hidrógeno restante, la densidad media de masa de plasma eólico solar a 1 UA es ${displaystyle 4times 10^{-21}traducidorho _{sw}(1) made10^{-20}$ (kg/m³).

En 1 UA la mayor parte de la investigación de vela magnética asume 6 protones por cm³ correspondiente a una densidad de ${displaystyle rho _{sw}(1)approx }$ 10^{20 - 20} y una velocidad del viento ${displaystyle v_{sw}$=500 km/s.

En promedio, la densidad de plasma disminuye con el cuadrado de la distancia del Sol mientras la velocidad es casi constante, véase Figura 4.2. La densidad media de masa como función de la distancia ${displaystyle a_{odot}$ Unidades astronómicas (AU) del Sol son:

${displaystyle rho _{sw}(a_{odot }=rho _{sw}(1)/a_{odot }{2}}$

()MO.1)

con la velocidad de plasma cayendo muy lentamente. El viento solar efectivo visto por una nave espacial viajando a velocidad ${displaystyle v_{sc}$ (significado positivo aceleración lejos de la estrella y significado negativo de la desaceleración hacia una estrella) es ${displaystyle U_{sw}=v_{sw}-v_{sc}$.

Deceleración en medio interestelar

Una nave espacial acelerada a velocidades muy altas por otros medios, como un cohete de fusión o una vela láser impulsada por láser, puede desacelerar incluso desde velocidades relativistas, sin necesidad de utilizar un propulsor a bordo mediante el uso de una vela magnética para generar resistencia contra el medio interestelar. entorno plasmático. Por ejemplo. misiones de larga duración, como misiones destinadas a ofrecer caminos evolutivos alternativos a la vida terrestre, p. según lo previsto por el proyecto Génesis, podría frenar pasivamente usando velas magnéticas al acercarse a una estrella distante.

El Sol es el centro de la región de la heliosfera que se extiende radialmente hacia afuera hasta un choque de terminación entre 75 y 90 AU, una heliovaina entre 80 y 100 AU y luego una heliopausa teórica entre 120 AU. Más allá de esto, hay una región de densidad relativamente baja llamada Burbuja Local que contiene una nube interestelar local (que contiene el Sistema Solar) y un complejo G-Cloud vecino que contiene Alpha Centauri. Se sabe menos sobre el ISM que dentro de la heliosfera, pero las mediciones de la Voyager 1 y la Voyager 2 han proporcionado datos importantes y las observaciones indirectas también han proporcionado información.

Estimaciones del número de partículas por cm³ son entre 0.005 y 0.5 en la burbuja local y G-cloud, respectivamente, lo que significa que la densidad de masa de plasma ISM ${displaystyle 6times 10^{-24}traducidorho _{im}traducido6times 10^{-22}$. Un valor típico asumido para acercarse a Alpha Centauri es el valor G-cloud de densidad de partículas de 0,1 partículas por cm³ correspondiente a ${displaystyle rho _{im}approx 10^{-22}$.

La velocidad de la nave espacial ${displaystyle v_{sc}$ es mucho mayor que la velocidad ISM al comienzo de una maniobra de desaceleración por lo que la velocidad de plasma efectiva es aproximadamente ${displaystyle v_{im}approx v_{sc}$.

Las emisiones de radio de la radiación ciclotron debido a la interacción de partículas cargadas en el medio interestelar, ya que espiral alrededor de las líneas de campo magnético de una vela magnética tendría una frecuencia aproximada (${displaystyle 120,v/c$) kHz, donde ${displaystyle v}$ es la velocidad de la nave espacial y ${displaystyle c}$ la velocidad de la luz. La ionosfera de la Tierra evitaría la detección en la superficie, pero una antena espacial podría detectar tales emisiones hasta varios miles de años luz. La detección de esa radiación podría indicar la actividad de civilizaciones extraterrestres avanzadas.

En una ionosfera planetaria

Una nave espacial que se acerca a un planeta con una atmósfera superior significativa, como Saturno o Neptuno, podría utilizar una vela magnética para desacelerar ionizando átomos neutros, como un plasma beta bajo. La velocidad de la nave espacial ${displaystyle v_{sc}$ es mucho mayor que la velocidad de ionosfera planetaria en una maniobra de desaceleración por lo que la velocidad de plasma efectiva es aproximadamente ${displaystyle v_{pi}approx v_{sc}$.

En una magnetosfera planetaria

Dentro o cerca de una magnetosfera planetaria, una vela magnética puede empujar o ser atraída por el campo magnético de un planeta creado por una dínamo, especialmente en una órbita que pasa sobre los polos magnéticos del planeta. Cuando la vela magnética y el campo magnético del planeta están en direcciones opuestas se produce una fuerza de atracción y cuando los campos están en la misma dirección se produce una fuerza de repulsión, que no es estable y es necesario un medio para evitar que la vela se vuelque.

El empuje que proporciona una vela magnética dentro de una magnetosfera disminuye con la cuarta potencia de su distancia desde el campo magnético interno del planeta. Cuando está cerca de un planeta con una fuerte magnetosfera como la Tierra o un gigante gaseoso, la vela magnética podría generar más empuje al interactuar con la magnetosfera en lugar del viento solar. Cuando se opera cerca de una magnetosfera planetaria o estelar, se debe considerar el efecto de ese campo magnético si es del mismo orden que el campo gravitatorio.

Al variar la fuerza del campo magnético y la orientación de la vela, se produce un "pateo de perigeo" se puede lograr elevando la altitud del apogeo de la órbita más y más alto, hasta que la vela magnética sea capaz de abandonar la magnetosfera planetaria y atrapar el viento solar. Se puede usar el mismo proceso a la inversa para bajar o circularizar el apogeo de la órbita de una vela magnética cuando llega a un planeta de destino con un campo magnético.

En teoría, es posible que una vela magnética se lance directamente desde la superficie de un planeta cerca de uno de sus polos magnéticos, repeliéndose a sí misma del campo magnético del planeta. Sin embargo, esto requiere que la vela magnética se mantenga en su estado "inestable" orientación. Un lanzamiento desde la Tierra requirió superconductores con 80 veces la densidad de corriente de los superconductores de alta temperatura más conocidos en 1991.

En 2022, una prueba de vuelo espacial denominada Experimento de velocidad de observación de Júpiter (JOVE) propuso usar un imán de plasma para desacelerar contra la magnetosfera de Júpiter.

Principios físicos

Los principios físicos involucrados incluyen: interacción de campos magnéticos con partículas cargadas en movimiento; un modelo de magnetosfera artificial análogo a la magnetosfera terrestre, MHD y modelos matemáticos cinemáticos para la interacción de una magnetosfera artificial con un flujo de plasma caracterizado por densidad y velocidad, y medidas de rendimiento; como la fuerza alcanzada, los requisitos de energía y la masa del sistema de vela magnética.

Interacción del campo magnético con partículas cargadas

Un ión o electrones con carga q en un plasma que se mueve a velocidad v en un campo magnético B y el campo eléctrico E es tratado como una carga de punto idealizada en la fuerza Lorentz ${displaystyle mathbf {F} =q,mathbf {E} +q,mathbf {v} times mathbf {B}$. Esto significa que la fuerza en un ion o electrones es proporcional al producto de su carga q y componente de velocidad ${displaystyle v}$ perpendicular al campo magnético B. Un diseño de vela magnética introduce un campo magnético en un flujo de plasma que bajo ciertas condiciones desvía los electrones y iones de su trayectoria original con el impulso de la partícula transferido a la vela y por lo tanto la nave espacial creando así empuje. Una vela eléctrica utiliza un campo eléctrico E que bajo ciertas condiciones interactúan con partículas cargadas para crear empuje.

Modelo magnetosférico artificial

Modelo magnetosférico artificial

Las características de la magnetosfera de la Tierra han sido ampliamente estudiadas como base para las velas magnéticas. La figura muestra las aerolíneas de partículas cargadas de un viento de plasma del Sol (o una estrella) o un viento eficaz cuando se desacelera en el ISM fluye de izquierda a derecha. Una fuente adjunta a una nave espacial genera un campo magnético. Bajo ciertas condiciones en el límite donde la presión magnética equivale a la presión cinética del viento de plasma una magnetopausia artificial forma a una longitud característica ${displaystyle L.$ m) de la fuente sobre el terreno. Las partículas de viento de plasma ionizado crean una hoja actual, conocida como la corriente Chapman-Ferraro a lo largo de la magnetopausia, que comprime las líneas de campo magnético frente al viento de plasma entrante por un factor de 2 en magnetopausia como se muestra en la Figura 2a. La magnetopausia desvía las partículas cargadas, lo que afecta sus aerosoles y aumenta la densidad en la magnetopausia. Una burbuja magnetosférica o formas de cavidad que tiene muy baja densidad aguas abajo de la magnetopausia. Arriba de la magnetopausia se desarrolla un choque de arco. Los resultados de simulación a menudo muestran la densidad de partículas mediante el uso del color con un ejemplo mostrado en la figura según la leyenda en la izquierda inferior. Esta figura utiliza aspectos de la estructura general de la Figura 3 Figura 1 y Figura 2a, y aspectos de la densidad plasmática de la Figura 1, y Figura 2.

Modelo magnetohidrodinámico

Los diseños de velas magnéticas que operan en un viento de plasma comparten una base teórica basada en un modelo magnetohidrodinámico (MHD), a veces llamado modelo fluido, de la física del plasma para una magnetosfera generada artificialmente. Bajo ciertas condiciones, el viento de plasma y la vela magnética están separados por una magnetopausa que bloquea las partículas cargadas, lo que crea una fuerza de arrastre que transfiere (al menos algo) el impulso a la vela magnética, que luego aplica empuje a la nave espacial adjunta.

Magneto artificial Modelo de Magnética Básica Sail

La figura representa el modelo MHD. Partiendo de la izquierda un viento de plasma en un ambiente de plasma (por ejemplo, estelar, ISM o una ionosfera) de velocidad efectiva ${textstyle v_{pe}}$ con densidad ${textstyle rho _{pe}$ (kg/m³) encuentra una nave espacial con velocidad de variando el tiempo ${textstyle v_{sc}$ (m/s) que es positivo si se acelera y es negativo si se desacelera. La velocidad aparente del viento de plasma desde el punto de vista de la nave espacial es ${textstyle U_{pe}=v_{pe}-v_{sc}$. La nave espacial y la fuente de campo generan un campo magnético que crea una burbuja magnetosférica extendiéndose a una magnetopausia precedida por un choque de arco que desvía electrones y iones del viento de plasma En magnetopause la presión magnética de la fuente de campo equivale a la presión cinética del viento de plasma en una posición que se muestra en la parte inferior de la figura. La longitud característica ${textstyle L}$ m) es la de una vela circular de zona de bloqueo eficaz ${displaystyle S=pi ,R_{mp} {2}$ Donde ${displaystyle R_{mp}approx L.$ es el radio imanopausia eficaz. En ciertas condiciones el viento plasma empujando sobre el choque de arco artificial de la magnetosfera y la magnetopausia crea una fuerza ${textstyle F_{w}$ (N) en la fuente de campo magnético que está físicamente ligada a la nave espacial para que al menos parte de la fuerza ${textstyle F_{w}$ Causa una fuerza ${textstyle F_{sc}$en la nave espacial, acelerando al navegar por el viento o desacelerando al navegar en un tobogán. En determinadas condiciones y en algunos diseños, algunas de las fuerzas de viento de plasma pueden perderse según lo indicado por ${textstyle F_{loss}$ en el lado derecho.

Todos los diseños de vela magnética suponen un enfrentamiento entre la presión del viento plasma ${displaystyle ¿Qué?$ y presión magnética ${textstyle P_{B}$ de la misma forma con parámetros específicos a un entorno de plasma, que difiere sólo en un coeficiente constante ${displaystyle C_{SO}$ como sigue:

${displaystyle ¿Qué? ¿Qué? {B_{mp} {2}{C_{SO}mu} ♪♪$

()MHD.1)

Donde ${textstyle u}$ (m/s) es la velocidad aparente del viento ${displaystyle rho }$(kg/m³) es la densidad del viento de plasma para un entorno de plasma específico, ${displaystyle B_{mp}$ (T) la fuerza de campo magnético en magnetopause, μ₀ (H/m) es la permeabilidad del vacío y ${textstyle C_{SO}$ es una constante que difiere por referencia como sigue ${textstyle C_{SO}=2}$ correspondiente a ${textstyle p_{w}$modelado como presión dinámica sin compresión de campo magnético, ${textstyle C_{SO}=1}$ para ${textstyle p_{w}$modelado como presión de carnero sin compresión de campo magnético y ${textstyle C_{SO}=1/2}$ para ${textstyle p_{w}$ modelado como presión de carnero con compresión de campo magnético por un factor de 2 Ecuación MHD.1 se puede resolver para producir el campo magnético requerido ${displaystyle B_{mp}$ (T) que satisface el equilibrio de presión en el standoff de magnetopause como:

$${displaystyle B_{mp}=u{sqrt {rho ,mu ¿Qué?$$

()MHD.2)

La densidad del plasma eólico solar disminuye en proporción inversa al cuadrado de la distancia ${displaystyle d}$ del Sol y por lo tanto de lo anterior, ${displaystyle B_{mp}$ disminución de la proporción inversa a ${displaystyle d}$. Desde la fuerza de campo magnético en radio ${displaystyle r}$ es ${displaystyle Bpropto 1/r^{3}$ esto significa que el radio magnético de vela magnetopause ${textstyle R_{mp}$ aumentará con la distancia del Sol, donde el mayor tamaño efectivo de una vela compensa la reducción de la presión dinámica del viento solar. La fuerza derivada de una vela magnética para un entorno de plasma se determina a partir de ecuaciones de MHD como reportan muchos investigadores es:

$${displaystyle ¿Por qué? {fnK} {fn}}f}fn}}pi}}}pi L^{2}}}}}} {f}}} {f}} {f}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {$$

()MHD.3)

Donde ${textstyle C_{d}$ es un coeficiente de arrastre determinado por análisis numéricos y/o simulación, ${textstyle rho u^{2}/2}$ (Pa) es la presión dinámica del viento, y ${displaystyle S=pi R_{mp} {2}$ (m²) es el área de bloqueo eficaz de la vela magnética con radio magnetopausia ${textstyle R_{mp}approx L.$ m). Tenga en cuenta que esta ecuación tiene la misma forma que la ecuación de arrastre en dinámicas de fluidos. ${textstyle C_{d}$ es una función de ángulo de ataque de la bobina sobre el empuje y el ángulo de dirección. El poder (W) del viento plasma es el producto de la velocidad y una fuerza constante

$${displaystyle ¿Por qué? rho {frac {fnK} {cH00}} {cH00}}} {cH00}}} {cH}}}}}} {f}}}}} {f}}} {f}}}}}}}} {f}}}}}}}}}}}}}}}} {f}} ¿Qué? {C_{d}upi }{2mu ¿Qué?$$

()MHD.4)

donde se usó la ecuación MHD.2 para derivar el lado derecho y se obtuvo el mismo resultado que la ecuación (9).

Prueba de aplicabilidad de MHD

A través del análisis, cálculo numérico, simulación y experimentación una condición importante para que una vela magnética genere fuerza significativa es la Prueba de aplicabilidad MHD, que declara que la distancia de separación ${displaystyle L.$ debe ser significativamente mayor que el ion gyroradius, también llamado el radio Larmor o ciclotron radio:

$${displaystyle r_{g}={frac {m_{i}v_{perp }{mid qmid B_{x}C_{Li}}}$$

()MHD.5)

Donde ${textstyle #$ (kg) es la masa ión, ${displaystyle v_{perp}$ (m/s) es la velocidad de iones perpendicular al campo magnético, ${displaystyle Silencioso$ (C) es la carga elemental del ión, ${textstyle B_{x}$ (T) es la fuerza de campo magnético en el punto de referencia ${textstyle x}$ y ${textstyle C_{Li}$ es una constante que difiere por fuente con ${textstyle C_{Li}=1}$ y ${textstyle C_{Li}=2}$. En el viento de plasma solar a 1 UA con ${displaystyle #$ (kg) la masa de protones, ${displaystyle vperp =v_{sw}$ = 500 km/s, ${displaystyle B_{x}=B_{mp}$ = 36 NT con ${displaystyle C_{SO}$=0.5 a partir de la ecuación MHD.2 en magnetopausa y ${textstyle C_{Li}$=2 entonces ${displaystyle.$ 72 km. La prueba de aplicabilidad MHD es la relación ${textstyle r_{g}/L}$. La figura trama ${displaystyle C_{d}$ en el eje izquierdo y perdido empuje en el eje derecho contra la relación ${textstyle r_{g}/L}$. Cuando ${displaystyle R_{g}/L$, ${displaystyle C_{d}=3.6}$ es máximo, a ${textstyle r_{g}/Lapprox 1}$, ${textstyle C_{d}=2.7}$, una disminución del 25% del máximo y al ${textstyle r_{g}/Lapprox 2}$, ${textstyle C_{d}approx 1.5}$, una disminución del 45%. As ${displaystyle R_{g}/L}$ aumenta más allá de uno, ${displaystyle C_{d}$ disminuye que significa menos empuje de las transferencias de viento de plasma a la nave espacial y se pierde al viento de plasma. En 2004, Fujita publicó análisis numéricos utilizando una simulación híbrida de PIC utilizando un modelo de dipolo magnético que trataba electrones como fluido y un modelo cinemático para iones para estimar el coeficiente de arrastre ${displaystyle C_{d}$ para una vela magnética operando en la orientación radial dando como resultado la siguiente fórmula aproximada:

$${displaystyle C_{d}(r_{g}/L)={begin{cases}3.6,e^{-0.28(r_{g}/L)^{2}, {3.4}{r_g}/L}e^{-0.22(L/r_{g})}{2}} {f}, {f}fnunci} }r_{g}/Lgeq 1end{cases}}$$

()MHD.6)

El empuje perdido es ${displaystyle T_{loss}=(1-C_{d}(r_{g}/L)/3.6}$.

Efecto del ángulo de ataque de la bobina sobre el empuje y el ángulo de dirección

Coil magnético campo orientación y fuerzas

En 2005 Nishida y otros publicaron resultados de análisis numéricos de un modelo MHD para la interacción del viento solar con un campo magnético de corriente fluyendo en una bobina que el impulso es efectivamente transferido al campo magnético producido por la fuente de campo y por lo tanto a la nave espacial. La fuerza de empuje deriva del cambio de impulso del viento solar, presión por el viento solar sobre la magnetopausia de la ecuación MHD.1 y la fuerza Lorentz de las corrientes inducidas en la magnetosfera interactuando con la fuente de campo. Los resultados cuantificaron el coeficiente de arrastre, dirección (es decir, dirección de empuje) ángulo con el viento solar, y par generado como una función de ángulo de ataque (es decir, orientación) La figura ilustra cómo el ángulo del ataque (o la inclinación de la bobina) ${displaystyle alpha _{t}$ la orientación de la bobina crea un ángulo de dirección para el vector de empuje y también torque impartido a la bobina. También se muestra el vector para el campo magnético interplanetario (IMF), que a 1 AU varía con ondas y otras perturbaciones en el viento solar, conocido como clima espacial.

Para una bobina con orientación radial (como un Frisbee) el ángulo de ataque ${displaystyle alpha _{t}$= 0 grados y con orientación axial (como un paracaídas) ${displaystyle alpha _{t}$= 90 grados. Los resultados de Nishida 2005 reportaron un coeficiente de arrastre ${displaystyle C_{d}$ que aumentó no linealmente con ángulo de ataque desde un mínimo de 3.6 en ${displaystyle alpha _{t}$=0 a un máximo de 5 a ${displaystyle alpha _{t}$= 90 grados. El ángulo de dirección del vector de empuje es sustancialmente inferior al ángulo de ataque de 45 grados debido a la interacción del campo magnético con el viento solar. Incrementos de torque ${displaystyle alpha _{t}$= 0 grados desde cero hasta un máximo ${displaystyle alpha _{t}$=45 grados y luego disminuye a cero a ${displaystyle alpha _{t}$= 90 grados. Varios diseños de vela magnética y otros papeles citan estos resultados. En 2012 Kajimura informó de resultados de simulación que cubrieron dos casos en los que la aplicabilidad del MHD ocurre con ${displaystyle R_{g}/L}$=1.125 y cuando se aplica un modelo cinemático ${displaystyle R_{g}/L}$=0.125 para calcular un coeficiente de arrastre ${displaystyle C_{d}$ y ángulo de dirección. Como se muestra en la Figura 4 de ese documento cuando la aplicabilidad del MHD ocurre los resultados son similares en forma a Nishida 2005 donde el mayor ${displaystyle C_{d}$ ocurre con la bobina en una orientación axial. Sin embargo, cuando se aplica el modelo cinemático, el mayor ${displaystyle C_{d}$ ocurre con la bobina en una orientación radial. El ángulo de dirección es positivo cuando el MHD es aplicable y negativo cuando se aplica un modelo cinemático. El 2012 Nishida y Funaki publicaron resultados de simulación para un coeficiente de arrastre ${displaystyle C_{D}$, coeficiente de elevación ${displaystyle C_{L}$ y un coeficiente de momento ${displaystyle C_{M}$ para un radio de bobina ${displaystyle R_{c}$=100 km y radio de magnetopausia ${displaystyle R_{mp}$=500 km a 1 UA. Estos resultados incluyeron el efecto del campo magnético interplanetario (IMF, que puede aumentar significativamente el empuje de una vela magnética a 1 AU).

Modelo de campo magnético

En un diseño, ya sea la fuerza del campo magnético o el radio magnetopausia ${displaystyle R_{mp}approx L.$ la longitud característica debe ser elegido. Una buena aproximación para una tasa de caída del campo magnético ${displaystyle f_{o},1leq f_{o}leq 3}$ para una distancia ${textstyle R_{0}leq rleq R_{mp}$ desde la fuente de campo a la magnetopausia comienza con la ecuación:

${displaystyle B(r)approx B(R_{0}{biggl (}{frac {R_{0}{r}}{biggr)} {f_{o}}}}} {f}}}} {f}}}} {f}}}}}} {f}}}}}}} {$

()MFM.1)

Donde ${displaystyle B(R_{0}}$ es el campo magnético en un radio ${displaystyle R_{0}$ cerca de la fuente de campo que cae cerca de la fuente como ${displaystyle 1/r^{3}$ como sigue:

${displaystyle B(R_{0})approx C_{0}{frac {mu _{0},mathbf {m} }{4,pi {fnMicrosoft Sans Serif}$

()MFM.2)

Donde ${displaystyle C_{0}$ es una constante multiplicando el momento magnético ${displaystyle mathbf {m}$ (A m²) para hacer ${displaystyle B(r)}$ coincide con un valor objetivo en ${textstyle r confía R_{0}$. Cuando está lejos de la fuente de campo, una dipole magnética es una buena aproximación y elegir el valor anterior ${displaystyle B(R_{0}}$ con ${displaystyle C_{0}$ =2 cerca de la fuente de campo fue utilizado por Andrews y Zubrin.

El modelo de bucle Amperian para el momento magnético es ${displaystyle mathbf {m} =I_{c}S}$, donde ${displaystyle I_{c}$ (A) is the current and ${displaystyle S=pi ,R_{c}{2}$ es la superficie (m²) para una bobina (arriba) de radio ${displaystyle R_{c}$m). Suponiendo que ${displaystyle R_{0}approx R_{c}$ y sustitución de la expresión por el momento magnético ${displaystyle mathbf {m}$ en la ecuación MFM.2 cede lo siguiente:

${displaystyle I_{c}={frac {4}{C_{0}mu} - Sí.$

()MFM.3)

Cuando el campo magnético fuente fuerza ${displaystyle B(R_{0}}$ se especifica, sustitución ${displaystyle B_{mp}$ del análisis del balance de presión de la ecuación MHD.2 y resolución para ${textstyle R_{mp}$ cede lo siguiente:

${displaystyle Lapprox R_{mp}approx ¿Qué?$

()MFM.4)

Esta es la expresión ${displaystyle L.$ cuando ${displaystyle f_{o}=3}$ con ${displaystyle C_{SO}=1/2}$ de la ecuación (4), con ${displaystyle C_{SO}=2}$ de la ecuación (4), y la distancia magnetopausa de la Tierra. Esta ecuación muestra directamente cómo una disminución de la tasa ${displaystyle f_{o}$ aumenta drásticamente el área de vela efectiva ${displaystyle S=pi R_{mp} {2}$ para un determinado momento magnético de origen de campo ${displaystyle mathbf {m}$ y ${displaystyle B_{mp}$ determinado por la ecuación de equilibrio de presión MHD.1. Sustituir esto en la ecuación MHD.3 produce la fuerza eólica de plasma como función de la tasa de declive ${displaystyle f_{o}$, densidad de plasma ${displaystyle rho }$ (kg/m³), radio de bobina ${displaystyle R_{c}approx R_{0}$ m), corriente de bobina ${displaystyle I_{c}$ (A) and plasma wind velocity ${displaystyle u}$ (m/s) as follows:

${displaystyle F_{w}(f_{o}={frac {C_{d}{2}rho u^{2},pi ,R_{0}\,{biggl (}{frac {B}}}{B_{0}}{biggr)}{2/f_{o}}}}={frac}} {f}}} {f}}} {f}}}}}} {f}}}}}} {f}}}}} {f}}}}} {f}}}}} {f}}}}} {f}} {f}}}}}}} {f}}}}}}}} {f}}}}} {f} {f} {f}}}}}}} {f}}}} {f}}} {f} {f}}}}}}}}} {f}}}}}}}}}}}}}}}}}} {f}}}}}}}} {C_{d}{2}rho u^{2},pi ,R_{0}{2},{biggl (}{frac {sqrt {msqrt {mu} {cH00} {cH00} {cH00} {ccH00}cH00}cH00}}cH00}}}cH00}cH00}ccH00}cH00}ccH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00cH00}cH00}cH00}cH00}cH00}cccH00}cH00}cH00}cH00} {fnMicrosoft Sans Serif}$

()MFM.5)

usando ecuación MFM.2 para ${displaystyle B(R_{0}}$ y ecuación MHD.2 para ${displaystyle B_{mp}$. Esta es la misma expresión que la ecuación (10b) cuando ${displaystyle f_{o}=3}$ y ${displaystyle C_{SO}=1/2}$, ecuación (108) y ecuación (5) con otros coeficientes numéricos agrupados en ${displaystyle C_{d}$ termino. Tenga en cuenta que la fuerza aumenta a medida que disminuye la tasa de declive.

Cuando el objetivo de diseño es el radio magnetopausia ${displaystyle R_{mp}$, la fuerza necesaria de la fuente de campo se determina directamente desde la ecuación MFM.1 como sigue:

${displaystyle B(R_{0}=B_{mp}{biggl (}{frac {R_{mp}{R_{0}}}{biggr)}} {f_{o}}}}} {f}}}} {f}}}}} {f}}}}}}} {f}}}}}}}} {$

()MFM.6)

que luego determina el momento magnético ${displaystyle mathbf {m}$ de la ecuación MFM.2 y la fuerza de viento plasma de la ecuación MHD.3.

Modelo cinemático general

Cuando la prueba de aplicabilidad de MHD ${textstyle r_{g}/L}$ 1 entonces un modelo de simulación cinemática predice con mayor precisión la fuerza transferida del viento plasma a la nave espacial. En este caso el área de bloqueo de vela efectiva ${displaystyle A_{e}$. ${displaystyle S=pi L^{2}$.

Fuerza de dipolo magnético: MHD y modelos cinemáticos

El eje izquierdo de la figura es para parcelas de fuerza de vela magnética versus longitud característica ${displaystyle L.$. La sólida línea negra traza la fuerza modelo MHD ${displaystyle F_{MHD}$ de la ecuación MHD.3. La línea verde muestra el valor de ion gyroradius ${displaystyle.$ 72 km de ecuación MHD.5. La línea azul desgarrada trama el modelo híbrido MHD/kinematic de la ecuación MHD.6 de Fujita04. La línea desgarrada roja trama una curva adecuada a los resultados de simulación de Ashida14. Aunque un buen ajuste para estos parámetros, el rango de curvas de este modelo no cubre algunos ejemplos relevantes. Los resultados adicionales de simulación de Hajiwara15 se muestran para el modelo MHD y cinemático como puntos de datos únicos como se indica en la leyenda. Estos modelos están de acuerdo. Los modelos cinemáticos predicen menos fuerza de lo que predijo el modelo MHD. En otras palabras, la fracción ${displaystyle T_{loss}$ de fuerza de empuje predicho por el modelo MHD se pierde cuando ${displaystyle R_{g}/L$ como trazado en el eje derecho. Las líneas azules y rojas sólidas muestran ${displaystyle T_{loss}$ para Fujita04 y Ashida18 respectivamente, indicando la operación con ${displaystyle L.$ menos del 10% ${displaystyle r_{g}$ tendrá una pérdida significativa. Otros factores en un diseño específico de vela magnética pueden compensar esta pérdida de valores ${displaystyle Lcantar_{g}$.

Medidas de desempeño

Las medidas importantes que determinan el rendimiento relativo de los diferentes sistemas de vela magnética incluyen: la masa del generador de fuentes de campo y sus necesidades de energía y energía; el empuje logrado; la relación de propulsión a peso, las limitaciones y limitaciones, y el sistema de propulsión agotado, si las hay. Masa de la fuente de campo ${displaystyle M_{fs}$ en el diseño de Magsail fue relativamente grande y los diseños posteriores se esforzaron para reducir esta medida. Total de las naves espaciales ${displaystyle M_{sc}=M_{fs}+M_{p}$, donde ${displaystyle M_{p}$ es la masa de carga útil. Las necesidades de energía son importantes en algunos diseños y se añaden a la masa de fuentes de campo. La fuerza de viento de plasma ${displaystyle F_{w}$ para un ambiente de plasma particular con aceleración ${displaystyle a=F_{w}/M_{sc}$. La relación de empuje a peso ${textstyle F_{w}/M_{sc}$es también una medida de rendimiento importante. Otras limitaciones y limitaciones pueden ser específicas para un diseño particular. Los diseños M2P2 y MPS, así como potencialmente el diseño del imán de plasma, agotan algún plasma como parte de inflar la burbuja magnetosférica y estos casos también tienen un impulso específico y una medida efectiva de rendimiento de la velocidad de escape.

Sistemas de vela magnética propuestos

Magsail (MS)

Andrews " Zubrin Magsail

La figura muestra el diseño de la lámina que consiste en un bucle de alambre superconductor de radio ${displaystyle R_{c}$ m) por orden de 100 km que tenga una corriente directa ${displaystyle I_{c}$ (A) que genera un campo magnético, que fue modelado según la ley Biot-Savart dentro del bucle y como dipolo magnético lejos fuera del bucle. Con respecto a la dirección del viento de plasma, un magsail puede tener una orientación radial (o normal) r una orientación axial que se puede ajustar para proporcionar el par para la dirección. En configuraciones no-axiales se genera elevación que puede cambiar el impulso de la nave espacial. El bucle se conecta a través de líneas shroud (o tethers) a la nave espacial en el centro. Debido a que un bucle que transporta corriente se ve obligado hacia fuera hacia una forma circular por su campo magnético, la vela podría ser desplegada por el cable conductor y la aplicación de una corriente a través de las plataformas periféricas. El bucle debe adjuntarse adecuadamente a la nave espacial para transferir el impulso del viento de plasma y sacar la nave espacial detrás de ella como se muestra en la configuración axial en el lado derecho de la figura.

Modelo MHD

El análisis del rendimiento de las mallas se realizó utilizando un modelo de simulación y fluido (es decir, MHD) con resultados similares observados para un caso. El momento magnético de un bucle corriente es ${displaystyle mathbf {m} =I_{c}pi R_{c} {2}$ para una corriente de ${textstyle I_{c}$ (A) and a loop of radius ${textstyle R_{c}$. Cerca del bucle, el campo magnético a distancia ${displaystyle z}$ a lo largo del eje central perpendicular al bucle se deriva de la ley Biot-Savart en la sección 5-2, ecuación (25) como sigue.

$${displaystyle B_{cl}(z)={frac {mu} ¿Por qué?$$

()MS.1)

A una distancia lejos del centro de bucle el campo magnético es aproximadamente el producido por un dipolo magnético. Puesto que la presión en el límite magnetosférico se duplica debido a la compresión del campo magnético y es el siguiente en un punto a lo largo del eje central a una distancia ${displaystyle z=L_{Z}$ para la distancia de separación de magnetopause objetivo de la ecuación (5).

${displaystyle ¿Qué? ¿Qué? {fnK} {fnK}} {fnK}} {f}}} {f}}} {f}}}} {f}}}}} {f}}}}}} {f}}}}}}}}} {\c}}}}}}} {\f}}}}}}}} {}}}}}}} {\\\\}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\c}}}}}}}}}}}}}}} Biggr.$

()MS.2)

equiparando esto a la presión dinámica para un ambiente de plasma ${fnMicrosoft Sans Serif}=rho {fnMicrosoft Sans Serif}$, inserción ${textstyle B_{cl}(0)}$ de la ecuación MS.1 y resolución para ${displaystyle L_{Z}$ rendimientos ecuación (6).

${displaystyle ¿Qué? {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}} {f}}}} {f}}}}}}} {\fnK}}}}}} {f}}}}} {f}}}}}}}}}}} {\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} Biggr.$

()MS.3)

Andrews y Zubrin derivan ecuación (8) para la fuerza de arrastre de la vela ${displaystyle F_{D}$ que determina la longitud característica ${displaystyle L_{Z}$ para un ángulo de inclinación, pero según la Sección 6.5 de Freeland se cometió un error en la integración numérica en la elección de la elipse río abajo desde la magnetopausia en lugar de la elipse río arriba que hizo que esos resultados optimistas por un factor de aproximadamente 3.1, que debe ser utilizado para corregir los resultados de la fuerza de arrastrar usando la ecuación (8). En cambio, este artículo utiliza la aproximación de la ecuación (108) para una burbuja esférica que corrige este error y está cerca de la fórmula analítica para la configuración axial como la fuerza para el Magsail como sigue:

${displaystyle F_{MS}=1.214,,{frac {rho ¿Qué? ¿Qué?$

()MS.4)

En 2004, Toivanen y Janhunen realizaron un análisis más profundo del Magsail al que llamaron MagnetoPausa Libre de Plasma (PFMP) que produjo resultados similares a los de Andrews y Zubrin.

Masa y corriente de la bobina (CMC)

La masa mínima requerida para transportar la corriente en la ecuación MS.1 u otros diseños de velas magnéticas se define en la ecuación (9) y la ecuación (3) de la siguiente manera:

${displaystyle M_{c}(min)=2,pi {fnMicrosoft Sans Serif} ¿Qué?$

()CMC.1)

Donde ${displaystyle J.$ (A/m²) es la densidad de corriente crítica superconductor y ${textstyle delta ¿Qué?$ (kg/m³) es la densidad de material de bobina, por ejemplo 6.500 para un superconductor. La masa física de la bobina es

${displaystyle M_{c}(phy)=(2,pi ,R_{c}+N_{tether}),pi ,r_{c}^{2},delta _{c}$

()CMC.2)

Donde ${displaystyle r_{c}$m) es el radio del alambre superconductor, por ejemplo, necesario para manejar la tensión para un caso de uso particular, con el ${displaystyle N_{tether}$ factor (p. ej., 3) contabilizar la masa de las líneas de tether (o shroud). Note que ${displaystyle M_{c}(phy)}$ con ${displaystyle N_{tether}$=0 debe ser no menos que ${displaystyle M_{c}(min)}$ para que la bobina lleve la corriente ${displaystyle I_{c}$. Ecuación de configuración CMC.2 con ${displaystyle N_{tether}$=0 igual a la ecuación CMC.1 y resolución para ${displaystyle r_{c}$ produce el radio mínimo requerido de la bobina

${displaystyle r_{c}(min)={sqrt {I_{c}/(J_{e}}}}$

()CMC.3)

Si se opera dentro del sistema solar, el alambre de superconductor de alta temperatura (HTS) es necesario para hacer que la salchicha práctica ya que la corriente requerida es grande. Sin embargo, la protección contra la calefacción solar es necesaria más cerca del Sol, por ejemplo por recubrimientos altamente reflectantes. Si se opera en superconductores de baja temperatura del espacio interestelar (LTS) podría ser adecuado ya que la temperatura de un vacío es de 2,7 K, pero la radiación y otras fuentes de calor de la nave espacial pueden hacer que LTS sea poco práctico. La capacidad de carga de corriente crítica del prometedor cable superconductor recubierto HTS YBCO aumenta a temperaturas inferiores con una densidad actual ${displaystyle J.$(A/m²) de 6x10¹⁰ a 77 K y 9x10¹¹ a las 5 K. La corriente crítica superconductora se define como ${displaystyle I_{cc}=J_{e}pi ¿Qué?$ (A) for a coil wire of radius ${displaystyle r_{c}$ m).

Modelo cinemático de Magsail (MKM)

La prueba de aplicabilidad MHD de la ecuación MHD.5 falla en algunos casos de desaceleración ISM y es necesario un modelo cinemático, como el documentado en 2017 por Claudius Gros resumido aquí. Una nave espacial con una masa general ${displaystyle m_{tot}$ y velocidad ${displaystyle v}$ sigue la ecuación (1) del movimiento como:

${displaystyle F_{MKM}=m_{tot}{dot {v}=-left(A_{G}(v)n_{p}vright)(2m_{p}v)=2,rho _{im},v^{2}A_{G}(v),}$

()MKM.1)

Donde ${displaystyle F_{MKM}$ (N) is force predicted by this model, ${displaystyle No.$ es la densidad de número de protón (m⁻³), ${displaystyle m_{p}$ es la masa protón (kg), ${displaystyle rho =m_{p}n_{p}$ (kg/m³) la densidad de plasma, y ${displaystyle A_{G}(v)}$ (m²) el área de reflexión efectiva. Esta ecuación supone que los encuentros de la nave espacial ${displaystyle A_{G}(v)n_{p}v}$ partículas por segundo y que cada partícula de masa ${displaystyle m_{p}$ queda reflejada. Tenga en cuenta que esta ecuación es de la misma forma que MFM.5 con ${displaystyle C_{d}$=4, interpretar el ${displaystyle C_{d}$ como un número.

Gros numerically determined the effective reflection area ${textstyle A_{G}(v)}$ integrando el grado de reflexión de acercarse a los protones interactuando con el campo magnético superconductor de bucle según la ley Biot-Savart. El resultado informado fue independiente del radio de bucle ${displaystyle R_{c}$. Una curva exacta como se indica en la Figura 4 a la evaluación numérica para el área de reflexión eficaz para una vela magnética en la configuración axial de la ecuación (8)

${displaystyle A_{G}(v)=0.081pi R_{c}{2}left[log left({frac] {cI}{vI_{G}}right)}{3}\,,v/c wonI/I_{G}$

()MKM.2)

Donde ${displaystyle pi R_{c} {2}$ (m²) es la zona cerrada por el bucle de carga actual, ${displaystyle c}$ (m/s) la velocidad de la luz, y el valor ${displaystyle I_{G}=1.55cdot 10^{6}$ (A) determined a good curve fit for ${displaystyle Yo...$= 10⁵ A, la corriente a través del bucle. En 2020, Perakis publicó un análisis que corroboraba la fórmula anterior con parámetros seleccionados para el viento solar y reportó una fuerza no más del 9% menos que el modelo Gros para ${displaystyle Yo...$= 10⁵ A y ${displaystyle R_{c}$=100 m con la bobina en una orientación axial.. Ese análisis también reportó sobre el efecto del ángulo de inclinación de la mariposa magsail en el ascensor y las fuerzas laterales para un caso de uso en la maniobra dentro del sistema solar.

A efectos de comparación, el área vélica efectiva determinada por Zubrin para la vela magnética a partir de la ecuación MS.3 con el factor de corrección 3,1 de Freeland aplicado y utilizando el mismo valor de velocidad (resolviendo la discrepancia señalada por Gros) como sigue:

${displaystyle A_{Z}(v)={frac {1.124times 1.26}{3.1}},L_{Z}}$

()MKM.3)

Magsail MHD y modelo cinemático eficaz zona de vela

La figura muestra el área de vela efectiva normalizada normalizada normalizada por el área de la bobina ${displaystyle pi R_{c} {2}$ para el caso MKM de Gros de ecuación MKM.1 y para Zubrin de la ecuación MKM.3 para ${displaystyle Iapprox I_{G}$, ${displaystyle R_{c}$=100 km, y ${displaystyle No.$=0.1 (cm^-3) para el G-cloud en acercamiento a Alpha Centauri correspondiente a la densidad ISM ${displaystyle rho _{im}=1.67times 10^{-22}$ (kg/m³) consistente con el de Freeland trazado contra la velocidad de la nave espacial relativa a la velocidad de la luz ${textstyle beta =v/c}$. Un buen ajuste ocurre para estos parámetros, pero para diferentes valores ${displaystyle R_{c}$ y ${displaystyle Yo...$ el ajuste puede variar significativamente. También está trazado la prueba de aplicabilidad MHD de ion gyroradius dividida por magnetopause radius ${displaystyle ¿Qué?$ ■1 de la ecuación MHD.4 en el eje secundario. Tenga en cuenta que la aplicabilidad de MHD ocurre en ${displaystyle v/c}$ para comparación, el 2004 Fujita ${displaystyle C_{d}$ como función de ${displaystyle ¿Qué?$ de la sección de prueba de aplicabilidad MHD también está trazado. Tenga en cuenta que el modelo Gros predice una disminución más rápida en el área efectiva que este modelo a velocidades superiores. Los valores normalizados de ${displaystyle A_{G}(v)}$ y ${displaystyle A_{Z}(v)}$ seguimiento de cerca hasta ${displaystyle beta =v/capprox}$ 10% después de qué punto el modelo de la Ecuación Zubrin magsail MS.4 cada vez más optimista y ecuación MKM.2 es aplicable en su lugar. Desde que los modelos siguen de cerca hasta ${displaystyle beta approx }$ 10%, con el modelo cinemático subestimando el área de vela efectiva para valores más pequeños ${displaystyle beta }$ (hence underestimating force), ecuación MKM.1 es una aproximación tanto para el MHD como para la región cinemática. El modelo Gros es pesimista ${displaystyle beta }$ 0,1%.

Gros utilizó la expresión analítica para el área de reflexión efectiva ${displaystyle A_{G}(v)}$ de la ecuación MKM.3 para la solución explícita de la distancia necesaria ${displaystyle x_{f}$ para desacelerar a la velocidad final ${displaystyle v_{f}approx 0.013c}$ de la ecuación (10) dada una velocidad inicial ${displaystyle V_{0}$ m/s) para una masa de naves espaciales ${displaystyle m_{tot}$ (kg) as follows:

${displaystyle x_{f}={frac {m_{tot},[g(v_{0}-g(v_{f}]}{0,081,m_{p},n_{p}pi} {fnMicrosoft Sans Serif}$

()MKM.4)

Donde ${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {cfnMicrosoft Sans Serif} - Sí.$. Cuando ${displaystyle v_{f}$=0 la ecuación anterior se define en la ecuación (11) como ${displaystyle x_{max}$, que permitió una solución de forma cerrada de la velocidad a distancia ${displaystyle x,v(x)}$ en ecuación (12) con integración numérica requerida para calcular el tiempo necesario para desacelerar en ecuación (14). Ecuación (16) utilizó este resultado para calcular y optimizar la corriente que minimiza ${displaystyle x_{max}$ como ${displaystyle I_{opt}=ebeta ¿Qué?$ Donde ${displaystyle beta ¿Qué?$. En 2017 Crowl optimiza la corriente de bobina para la relación de área efectiva ${displaystyle A(v)}$ sobre la masa total ${displaystyle m_{tot}$ y derivado del resultado ${displaystyle I_{opt}=e^{3}beta ¿Qué?$ en ecuación (15). Ese artículo utilizó resultados de Gros para la distancia de parada ${displaystyle x_{max}$ y tiempo para desacelerar.

Magsail ISM de aceleración distancia y comparación de tiempo

La figura traza la distancia viajada mientras desacelera ${displaystyle x_{d}$ (ly) and time required to decelerate ${displaystyle T_{d}$ (yr) dada una velocidad relativa inicial ${displaystyle beta ¿Qué?$ y una velocidad final ${displaystyle v_{f}=0.013c}$ (m/s) consistente con el de Freeland para los mismos parámetros arriba. Ecuación CMC.1 da la masa de los magsales ${displaystyle M_{s}$ como 97 toneladas suponiendo 100 toneladas de masa de carga útil ${displaystyle M_{p}$ utilizando los mismos valores utilizados por Freeland de ${displaystyle J.$ = 10¹¹ (A/m²) y ${displaystyle delta _{c}$= 6.500 (kg/m³) para la bobina superconductora. Ecuación MS.4 da Fuerza para el escudo multiplicado por ${displaystyle C_{d}$=4 para el modelo Andrews/Zubrin para alinearse con la ecuación MHD.3 definición de fuerza del modelo Gros. La aceleración es la fuerza dividida por masa, la velocidad es la parte integral de la aceleración sobre el intervalo de tiempo de desaceleración ${displaystyle T_{d}$ (yr) and deceleration distance traveled ${displaystyle x_{d}$ (ly) es la parte integral de la velocidad sobre ${displaystyle T_{d}$ (yr). La integración numérica dio lugar a las líneas trazadas en la figura con distancia de desaceleración trazada sobre el eje vertical primario a la izquierda y el tiempo necesario para desacelerar en el eje vertical secundario a la derecha. Tenga en cuenta que el modelo MHD Zubrin y el modelo kinematic Gros predicen valores casi idénticos de distancia de desaceleración hasta ${displaystyle beta ¿Qué?$~ 5% de la velocidad de la luz, con el modelo Zubrin prediciendo menos distancia de desaceleración y menor tiempo de desaceleración a mayores valores ${displaystyle beta ¿Qué?$. Esto es consistente con el modelo Gros que predice un área más pequeña efectiva ${displaystyle A(v)}$ a valores más grandes de ${displaystyle beta ¿Qué?$. El valor de la solución de forma cerrada para la distancia de desaceleración ${displaystyle x_{f}$desde MKM.4 para los mismos parámetros sigue de cerca el resultado de integración numérica.

Diseños específicos y perfiles de misión

En 1990 Andrews y Zubrin informaron sobre un ejemplo para los parámetros de viento solar uno AU lejos del Sol, con ${textstyle n_{i}=5times 10^{6}$ (m⁻³) con sólo protones como iones, velocidad aparente del viento ${textstyle u_{sw}$=500 (km/s) la fuerza de campo necesaria para resistir la presión dinámica del viento solar es 50 nT de la ecuación MHD.2. Con radio ${displaystyle R_{c}$=100 km y burbuja magnetosférica de ${textstyle L}$=500 km (310 mi) reportaron un empuje de 1980 newtons y una masa de bobina de 500 toneladas. Para los parámetros anteriores con el factor de corrección de 3.1 aplicado a la ecuación MS.4 produce el mismo empuje y ecuación CMC.1 produce la misma masa de bobina. Se reportaron resultados para otros 4 casos de viento solar, pero la prueba de aplicabilidad MHD de la ecuación MHD.5 falló en estos casos.

En 2015 Freeland documentó en detalle un caso de desaceleración interestelar para acercarse a Alpha Centaturi como parte de un estudio para actualizar Project Icarus con ${displaystyle R_{c}$=260 km, una inicial ${textstyle R_{mp}$ de 1.320 km y densidad ISM ${displaystyle rho _{im}=1.67times 10^{-22}$ kg/m³, casi idéntico a la medida n(H I) de 0.098 cm⁻³ por Gry en 2014. El estudio Freeland predijo la desaceleración del 5% de la velocidad de luz en aproximadamente 19 años. Los parámetros de la bobina ${displaystyle J.$= 10¹¹ (A/m²), ${displaystyle r_{sc}$= 5 mm, ${displaystyle rho _{sc}$= 6.500 (kg/m³), resultó en una masa de bobina estimada ${displaystyle M_{c}(phy)}$= 1.232 toneladas. Aunque la densidad de corriente crítica ${displaystyle J.$ se basó en un informe de 2000 Zubrin NIAC proyectando valores hasta 2020, el valor asumido está cerca de eso para el cable superconductor de producción comercial YBCO en 2020. La estimación masiva puede ser optimista ya que supone que toda la bobina que transporta masa es superconducting mientras que las técnicas de fabricación 2020 colocan una película delgada en un sustrato no superconductor. Para la densidad de plasma media interestelar ${displaystyle rho _{im}}$= 1,67x10⁻²² con una velocidad aparente de viento 5% de velocidad de luz, el ion gyroradius es de 570 km y por lo tanto el valor de diseño para ${textstyle R_{mp}$ cumple con la prueba de aplicabilidad MHD de la ecuación MHD.5. Ecuación MFM.3 da la corriente de bobina requerida como ${displaystyle I_{c}$~7,800 kA y de la ecuación CMC.1 ${displaystyle M_{c}(min)}$= 338 toneladas; sin embargo, pero el radio mínimo de alambre superconductor correspondiente de la ecuación CMC.3 es ${displaystyle r_{c}(min)}$ =1 mm, que sería insuficiente para manejar la fuerza de empuje desacelerante ${displaystyle F_{MS}$ ~ 100.000 N predicho por ecuación MS.4 y por lo tanto el diseño especificado ${displaystyle r_{sc}$= 5 mm para cumplir con los requisitos estructurales. En un diseño completo, también debe incluirse la masa de blindaje de la bobina para mantener la temperatura crítica y sobrevivir a la abrasión en el espacio exterior y en otras infraestructuras. Apéndice Una estimación de estos como 90 toneladas para blindaje de alambre y 50 toneladas para las carretillas y otras infraestructuras de lavado. Freeland comparó este diseño de desaceleración con uno en el que tanto la aceleración como la desaceleración fueron realizados por un motor de fusión y reportó que la masa de un diseño de "Icarus sucio" fue más del doble que con el Magsail utilizado para la desaceleración. Un diseño de Icarus publicado en 2020 utilizó una unidad de fusión Z-pinch en un enfoque llamado Firefly que redujo drásticamente la masa de la unidad de fusión y hizo que la fusión sólo lograra un rendimiento comparable al diseño de fusión y de velas.

En 2017 Gros reportó ejemplos numéricos para el modelo cinemático Magsail que utiliza diferentes parámetros y modelos de masa de bobina que los utilizados por Freeland. Para una misión de alta velocidad a Alpha Centauri con velocidad inicial antes de la desaceleración ${displaystyle v_{0}=c/10}$ utilizando una masa de bobina de 1500 toneladas y un radio de bobina ${displaystyle R.$= 1600 km. La distancia de parada estimada fue ${displaystyle x_{max}$de 0,37 (sólo) y un tiempo total de viaje de 58 años, siendo 1/3 la desaceleración.

En 2017, Crowl documentó un diseño para una misión que comenzaba cerca del Sol y tenía como destino el Planeta 9 a una distancia aproximada de 1000 UA que empleaba el modelo cinemático Magsail. El diseño tuvo en cuenta la gravedad del Sol, así como el impacto de la temperatura elevada en la bobina superconductora, compuesta de hidrógeno metálico metaestable, que tiene una densidad de masa de 3500 (kg/m³) aproximadamente la mitad que la de otros superconductores. El perfil de la misión usó Magsail para acelerar alejándose de 0.25 a 1.0 AU del Sol y luego usó Magsail para frenar contra el ISM local en la aproximación al Planeta nueve por un tiempo total de viaje de 29 años. Los parámetros y los modelos de masa de la bobina difieren de los utilizados por Freeland.

Otro perfil de misión utiliza un velo orientado a un ángulo de ataque para lograr la transferencia heliocéntrico entre planetas que se alejan del Sol o hacia él. En 2013 Quarta y otros utilizaron los resultados de simulación de Kajimura 2012 que describieron el ascensor (ángulo inclinado) y el par para lograr una órbita de transferencia Venus a la Tierra de 380 días con un radio de bobina ${displaystyle R_{c}$~1 km con aceleración característica ${displaystyle A_{c}$=1 mm/s². En 2019 Bassetto y otros utilizaron el modelo de magnetopausia Quarta y predijo una órbita de transferencia Venus a la Tierra de aproximadamente 8 años para un radio de bobina ${displaystyle R_{c}$~1 km. con aceleración característica ${displaystyle A_{c}$=0,1 mm/s². En 2020 Perakis utilizó el modelo cinemático Magsail con un radio de bobina ${displaystyle R_{c}$=350 m, corriente ${displaystyle I_{c}$= 10⁴ A y masa de naves espaciales de 600 kg que cambiaron el ángulo de ataque para acelerar lejos de la órbita terrestre y desacelerar a la órbita de Júpiter dentro de 20 años.

Mini-propulsión de plasma magnetosférico (M2P2)

Winglee M2P2 esquema

En 2000 Winglee y otros propusieron una orden de diseño para reducir el tamaño y el peso de una vela magnética y la nombraron propulsión de plasma minimagnetosférico (M2P2). La figura basada en ilustra el diseño M2P2, que es el mismo que el diseño de la vela de plasma Magneto. Comenzando en el centro con una bobina solenoide de radio ${displaystyle R_{H}$ m) de ${textstyle N_{t}$=1,000 vueltas portando una corriente de radio frecuencia que genera una onda de helicona que inyecta plasma alimentado de una fuente en una bobina de radio ${textstyle R_{c}$ m) que lleve una corriente de ${displaystyle I_{c}$ (A), que genera un campo magnético. El plasma inyectado excitado mejora el campo magnético y genera una magnetosfera miniaturizada alrededor de la nave espacial, análoga a la heliopausa donde el Sol inyectado plasma encuentra el medio interestelar, las eyecciones de masa coronal o el magnetotail de la Tierra. El plasma inyectado creó un ambiente que el análisis y las simulaciones mostraban tenía un campo magnético con una tasa de declive ${displaystyle 1/r}$ en comparación con el modelo clásico de un ${textstyle 1/r^{3}$ tasa de declinación, haciendo la bobina mucho más pequeña significativamente más eficaz. La presión del plasma inflado junto con la presión de campo magnético más fuerte a una distancia mayor debido a la baja tasa de declive estiraría el campo magnético e inflaría una burbuja magnetosférica alrededor de la nave espacial.

El papel Winglee 2000 describió un diseño y reportó resultados adaptados de la magnetosfera de la Tierra. Parameters for the coil and solenoid were ${displaystyle R_{H}$=2.5 cm y para la bobina ${textstyle R_{c}$= 0,1 m, 6 órdenes de magnitud menos que la bobina de la vela con masa correspondientemente mucho menor. Una estimación para el peso de la bobina fue de 10 kg y 40 kg para la fuente de inyección de plasma y otra infraestructura. Resultados notificados de la Figura 2 ${displaystyle B_{0}approx }$ 4x10-3 T en ${displaystyle R_{mp}approx }$ 10 km y de la Figura 3 un resultado extrapolado con una fuerza de inyección de plasma ${textstyle F_{jet}approx}$10⁻³ N resulta en una fuerza de empuje ${textstyle F_{M2P2}approx }$ 1 N. La fuerza de navegación magnética de la ecuación MHD.3 es ${displaystyle F_{w}$=3x10^{−11 -} N y por lo tanto M2P2 reportó una ganancia de impulso de 4x10¹⁰.

Desde M2P2 inyecta gas ionizado a un ritmo ${displaystyle #$(kg/s) que se puede ver como un propulsor tiene un impulso específico ${displaystyle I_{sp}=F_{M2P2}/m_{in}/g_{0}$ Donde ${displaystyle G_{0}$ (m/s²) es la aceleración de la gravedad de la Tierra. Winglee declaró ${displaystyle #$=0.5 (kg/día) y, por consiguiente ${displaystyle I_{sp}$=17.621. La velocidad de escape equivalente ${displaystyle ¿Qué?$ es de 173 km/s para 1 N de fuerza de empuje. Winglee asumió la masa total propelente de 30 kg y por lo tanto propelente se agotaría en 60 días.

En 2003, Khazanov publicó MagnetoHydroDynamic (MHD) y estudios cinéticos que confirmaron algunos aspectos de M2P2 pero plantearon cuestiones que el tamaño de la vela era demasiado pequeño, y que el empuje muy pequeño resultaría y también concluyó que la hipótesis ${textstyle 1/r}$ la tasa de caída del campo magnético estaba más cerca ${textstyle 1/r^{2}$. Las parcelas de densidad de plasma de Khazanov indicaron una densidad relativamente alta dentro de la burbuja magnetosférica en comparación con la región del viento solar externo que difiere significativamente de las publicadas por Winglee donde la densidad dentro de la burbuja magnetosférica era mucho menos que fuera en la región del viento solar externo.

Un análisis detallado de Toivanen y otros en 2004 comparó un modelo teórico de Magsail, apodado Plasma-free Magnetospheric Propulsion (PFMP) versus M2P2 y concluyó que la fuerza de empuje predicho por Winglee y otros fue más de diez órdenes de magnitud optimista ya que la mayoría del impulso del viento solar se entregó al magnetotail y las fugas actuales a través de la magnetopausia y no al espacio. Sus comentarios también indicaron que las líneas de campo magnético pueden no estar lo suficientemente cerca de la bobina para lograr una transferencia significativa de fuerza. Su análisis hizo una analogía con la hoja de corriente heliosférica como ejemplo en la astrofísica donde el campo magnético podría caerse a una tasa de entre ${textstyle 1/r}$ y ${textstyle 1/r^{2}$. También analizaron las hojas actuales reportadas por Winglee desde la magnetopausia hasta la nave espacial en la dirección hacia el viento y una hoja actual en el magnetotail. Su análisis indicó que las hojas actuales debían pasar muy cerca de la nave espacial para impartir una fuerza significativa podían generar calor significativo y hacer que esta palanca fuera poco práctica.

En 2005, Cattell y otros publicaron comentarios sobre M2P2 que incluían la falta de conservación del flujo magnético en la región fuera de la magnetosfera que no se consideraba en los estudios de Khazanov. Su análisis concluyó en la Tabla 1 que Winglee había subestimado significativamente el tamaño de la vela requerido, la masa, requería flujo magnético y afirmó que la hipótesis ${textstyle 1/r}$ El descenso del campo magnético no era posible.

La expansión del campo magnético utilizando plasma inyectado se demostró en una gran cámara de vacío en la Tierra, pero la cuantificación del empuje no formó parte del experimento. La presentación adjunta tiene algunas buenas animaciones que ilustran los principios físicos descritos en el informe. Un artículo de Winglee de 2004 se centró principalmente en el uso de M2P2 para blindaje electromagnético. A partir de 2003, el diseño de la vela de plasma Magneto investigó más a fondo el aumento del campo magnético por inyección de plasma, usó bobinas más grandes y reportó ganancias más modestas.

Vela de magnetoplasma (MPS)

En 2003 Funaki y otros propusieron un enfoque similar al diseño M2P2 y lo llamaron MagnetoPlasma Sail (MPS) que comenzó con una bobina ${displaystyle R_{c}$=0,2 m y una tasa de caída del campo magnético ${displaystyle f_{o}$=1.52 con plasma inyectado creando un radio de vela eficaz ${displaystyle L.$=26 km y asumió una eficiencia de conversión que transfirió una fracción del impulso del viento solar a la nave espacial. Los resultados de la simulación indicaron un aumento significativo del tamaño de la magnetosfera con inyección de plasma en comparación con el diseño de Magsail, que no tenía inyección de plasma. El análisis mostró cómo el ajuste del ángulo de dirección MPS creó la fuerza que podría alcanzar los planetas externos. Se propuso un ensayo por satélite. Se notificaron los resultados preliminares del desempeño, pero posteriormente se modificaron en documentos posteriores.

Se han publicado muchos artículos de MPS sobre la vela magnética que contribuyen a la comprensión de los principios físicos generales de una magnetosfera artificial, su modelo magnetohidrodinámico y el enfoque de diseño para calcular la distancia de la magnetopausa para una fuente de campo magnético determinada se documentan en el vínculo secciones de este artículo.

En 2004 Funaki y otros analizaron casos de MPS donde ${displaystyle R_{c}$=10 m y ${displaystyle R_{c}$=100 m como se resume en la tabla 2 prediciendo una longitud característica ${displaystyle L.$ de 50 y 450 km produciendo un empuje significativo con masa sustancialmente menor que el Magsail y por lo tanto una aceleración significativa. Este artículo detalló la prueba de aplicabilidad MHD de la ecuación MHD.5 que la longitud característica debe ser mayor que el ion gyroradius ${displaystyle r_{g}$ m) transferir eficazmente el impulso del viento solar a la nave espacial. En 2005 Yamakawa y otros describieron un posible juicio.

Una analogía con la magnetosfera de la Tierra y la magnetopausia para determinar la penetración de las irregularidades plasmáticas en la magnetopausia define el parámetro clave de una beta de plasma cinético local como la relación de la presión dinámica ${displaystyle p_{dyn}$del plasma inyectado sobre la presión magnética ${displaystyle p_{dyn}$ como sigue:

${displaystyle beta ¿Qué? {fnh} {fnh} {fnh00} {fnh} {fnh} {fnh}} {fnh}}} {fnh} {fnh} {fnhfnh} {fnh}} {f}}}}} {fnfnf}fnfnf}}}fnf}}fnfnfnH00}}fnfnKfnH00}fnKfnKfnKfnKfnKfnKfnKf}}}}}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}fn\\fnKf}fnKfnKfnKfnKfnKfnKfnKfnKf}fnK ♪♪$

()MPS.1)

Donde ${displaystyle rho _{l}$ (kg/m³) es la densidad de plasma local, ${textstyle u_{l}$ (m/s) es la velocidad local del plasma y ${displaystyle B_{l}$ (T) es el campo magnético local. Las simulaciones han demostrado que la beta cinética es más pequeña cerca de la fuente de campo, en magnetopausia y el choque de arco.

El cinético ${displaystyle beta _{k}$ difiere de la beta de plasma térmico ${textstyle beta ¿Qué?$ silencia la relación de la presión térmica plasmática a la presión magnética, con términos: ${displaystyle P_{plasma}=n,k_{B},T}$ es la presión plasmática con ${displaystyle n}$ (m⁻³) la densidad número, ${displaystyle K_{B}$ (J/K) la constante de Boltzmann ${displaystyle T}$ (eV) la temperatura ion; y ${textstyle p_{mag}=B^{2}/(2mu _{0}}$presión magnética para el campo magnético ${displaystyle B}$ (T) and ${displaystyle mu _{0}}$ (H/m) permeabilidad al vacío. En el contexto del MPS, ${displaystyle beta _{k}$ determina la propensión del flujo de plasma inyectado para estirar el campo magnético mientras ${displaystyle beta _{i}$ especifica la energía relativa del plasma inyectado.

En 2005 Funaki y otros publicaron análisis numéricos ${displaystyle f_{0}$=1.88 para ${displaystyle beta _{k}$=0.1. En 2009 Kajimura publicó resultados de simulación con ${displaystyle beta _{k}$=5 y ${displaystyle beta _{i}$ de 6 a 20 que la tasa de caída del campo magnético ${displaystyle f_{0}$ con argón y plasma xenón inyectado en la región polar ${displaystyle f_{0}$=2.1 y con plasma argón inyectado en la región ecuatorial fue ${displaystyle f_{0}$= 1,8.

Si ${displaystyle beta _{k} título1}$ entonces la inyección de un plasma de alta velocidad y alta densidad en una magnetosfera como se propone en M2P2 congela el movimiento de un campo magnético en el flujo de plasma y se cree que infla la magnetosfera. Sin embargo, experimentos y análisis numéricos determinaron que el viento solar no puede comprimir la magnetosfera y la transferencia de impulso a la nave espacial es limitada ya que el impulso se transfiere al plasma inyectado que fluye de la magnetosfera, similar a otra crítica de M2P2.

Esquemática de vela Magnetoplasma (MPS)

Una alternativa es reducir la velocidad y densidad de inyección de plasma para resultar en ${displaystyle beta _{k}traducido1}$ para lograr un plasma en equilibrio con el campo magnético inflado y, por lo tanto, inducir una corriente diamagnética ecuatorial en la misma dirección que la corriente de bobina que se muestra en la figura, aumentando así el momento magnético de la fuente de campo MPS y aumentando así el empuje. En 2013 Funaki y otros publicaron simulación y resultados teóricos sobre cómo las características del plasma inyectado afectaron la ganancia de impulso mediante la creación de una corriente de anillo ecuatorial. Definieron la ganancia de empuje para MPS como ${displaystyle G_{MPS}=F_{MPS}/F_{mag}$: la relación de la fuerza generada por baja inyección de plasma beta ${displaystyle F_{MPS}$ dividido por el de una vela magnética pura ${displaystyle F_{mag}$ de la ecuación MFM.5 con ${textstyle f_{o}=3}$ y ${displaystyle C_{SO}=0.5}$ para ${displaystyle r_{g}leq L.$ o de la ecuación GKM.1 para ${displaystyle r_{g}]$. They reported ${displaystyle G_{MPS}$ de aproximadamente 40 para las magnetosferas menos que la prueba de aplicabilidad del MHD y 3.77 para una magnetosfera más grande donde ocurrió la aplicabilidad del MHD, mayores que los valores reportados en 2012 de 20 y 3.3, respectivamente. Las simulaciones revelaron que el aumento óptimo del empuje ocurrió para ${displaystyle beta _{k}traducido1}$ y ${displaystyle beta _{i}approx 10}$.

En 2014 Arita, Nishida y Funaki publicaron resultados de simulación indicando que la inyección de plasma creó una corriente de anillo ecuatorial y que la tasa de inyección de plasma tuvo un impacto significativo en el rendimiento del empuje, con el valor más bajo simulado teniendo el mejor rendimiento de una ganancia de empuje ${displaystyle G_{MPS}$ de 3,77 con ${displaystyle beta _{i}approx 25}$. También reportaron que MPS aumentó la altura de la magnetosfera por un factor de 2.6, que es importante ya que aumenta el área de bloqueo de vela efectiva.

En 2014 Ashida y otros documentaron resultados de simulación de partículas en células (PIC) para un modelo cinemático para casos donde ${displaystyle r_{g} L.$ donde el MHD no es aplicable. La ecuación (12) de su estudio incluyó la fuerza adicional del jet de plasma inyectado ${displaystyle F_{jet}$ que consiste en el impulso y la presión estática de iones y electrones y la ganancia de empuje definida como ${textstyle F_{MPS}/(F_{mag}+F_{jet}}$, que difiere de la definición de un término por el mismo nombre en otros estudios. Representa la ganancia de MPS sobre la de simplemente agregar la fuerza de vela magnética y la fuerza de inyección de plasma. Para los valores citados en la conclusión, ${displaystyle F_{MPS}/F_{mag}$ es 7.5 en la orientación radial.

Resumen de los resultados de los resultados de los resultados de los resultados de los resultados de los resultados de los resultados

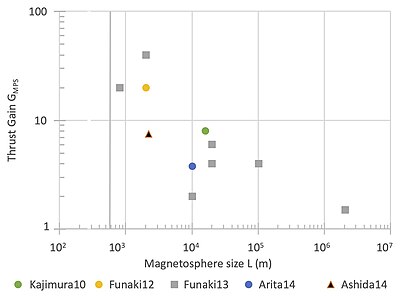
Puesto que varios resultados fueron publicados por diferentes autores en diferentes momentos, la figura resume el aumento de impulso reportado ${displaystyle G_{MPS}$ frente al tamaño de la magnetosfera (o longitud característica) ${displaystyle L.$) con la fuente indicada en la leyenda como sigue para los resultados de simulación Arita14, Ashida14, Funaki13, y Kajimura10. Los resultados de simulación requieren un tiempo de cálculo significativo, por ejemplo, tomó 1024 CPUs 4 días para simular el caso más simple y 4096 CPUs una semana para simular un caso más complejo. Una ganancia de empuje entre 2 y 10 es común con las mayores ganancias con un plasma de inyección de boquilla magnética en una dirección en oposición al viento solar. La prueba de aplicabilidad MHD de la ecuación MHD.5 para el viento solar es ${displaystyle Lapprox}$72 km. Por lo tanto, la fuerza estimada del MPS es la de la ecuación MHD.3 multiplicado por la ganancia de empíricamente determinada ${displaystyle G_{MPS}$ de la figura multiplicada por el porcentaje de pérdida de empuje ${displaystyle T_{loss}$ de la ecuación MHD.6

${displaystyle ¿Qué? L^{2},,,r_{g}leq L.$

()MPS.2)

Por ejemplo, utilizando parámetros de viento solar ${displaystyle rho }$=8x10^{,21 - 21} kg/m³ y ${displaystyle u}$= 500 km/s entonces ${displaystyle r_{g}$=72 km y ${displaystyle B_{mp}$=4x10⁻⁸ T. Con ${displaystyle L.$= 10⁵ m para ${displaystyle f_{o}$=3 entonces ${displaystyle - No.$ y ${displaystyle T_{loss}approx }$ 11% de la ecuación MHD.6. El campo magnético sólo fuerza con un radio de bobina ${displaystyle R_{c}$= 6.300 m y corriente de bobina ${displaystyle I_{c}$= 1,6x10⁶ Un rendimiento ${displaystyle B_{0}$= 1,6x10⁻⁴ T de la ecuación MFM.2 y con ${displaystyle C_{d}$=5 la fuerza magnética sólo es 175 N de la ecuación MFM.5. Determinación ${displaystyle G_{MPS}approx }$4 de la cifra ${displaystyle L.$= 10⁵ m como el multiplicador de la fuerza magnética-sólo la fuerza MPS ${displaystyle F_{MPS}approx }$700 N.

Desde MPS inyecta gas ionizado a una tasa ${displaystyle #$(kg/s) que se puede ver como un propulsor tiene un impulso específico ${displaystyle I_{sp}=F_{MPS}/m_{in}/g_{0}$ Donde ${displaystyle G_{0}$ (m/s²) es la aceleración de la gravedad de la Tierra. Funaki y Arita declararon ${displaystyle #$=0.31 (kg/día). Por lo tanto ${displaystyle I_{sp}$=28.325 (s) por newton de fuerza de empuje. La velocidad de escape equivalente ${displaystyle ¿Qué?$ es 278 km/s por newton de fuerza de empuje.