Variables de mandelstam

En física teórica, las variables de Mandelstam son cantidades numéricas que codifican la energía, el momento y los ángulos de las partículas en un proceso de dispersión de forma invariante de Lorentz. Se utilizan para procesos de dispersión de dos partículas a dos partículas. Las variables de Mandelstam fueron introducidas por primera vez por el físico Stanley Mandelstam en 1958.

Si la métrica de Minkowski es elegida diag()1,− − 1,− − 1,− − 1){displaystyle mathrm {diag} (1,-1,-1,-1)}, las variables Mandelstam s,t,u{displaystyle s,t,u} son entonces definidos por

• s=()p1+p2)2c2=()p3+p4)2c2{displaystyle s=(p_{1}+p_{2}){2}c^{2}=(p_{3}+p_{4})^{2}c^{2}}
• t=()p1− − p3)2c2=()p4− − p2)2c2{displaystyle t=(p_{1}-p_{3}){2}c^{2}=(p_{4}-p_{2})^{2}c^{2}}
• u=()p1− − p4)2c2=()p3− − p2)2c2{displaystyle u=(p_{1}-p_{4})^{2}c^{2}=(p_{3}-p_{2})}{2}c^{2}},

donde p₁ y p₂ son los cuatro momentos de las partículas entrantes y p₃ y p₄ son los cuatro momentos de las partículas salientes.

s{displaystyle s} es también conocido como la plaza de la energía centro de masa (masa invariante) y t{displaystyle t} como el cuadrado de la transferencia de cuatro meses.

Diagramas de Feynman

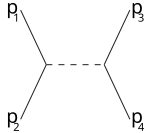
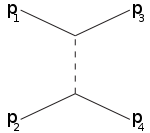
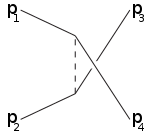
Las letras s,t,u también se utilizan en los términos canal-s (canal temporal), canal-t y canal u (ambos canales espaciales). Estos canales representan diferentes diagramas de Feynman o diferentes posibles eventos de dispersión donde la interacción implica el intercambio de una partícula intermedia cuyo momento de cuatro cuadrados es igual a s,t,u, respectivamente.

s-cannel	t-canal	u-canal

Por ejemplo, el canal s corresponde a las partículas 1,2 que se unen en una partícula intermedia que finalmente se divide en 3,4: el canal s es la única forma de descubrir resonancias y nuevas partículas inestables, siempre que sus vidas sean lo suficientemente largas como para que sean detectables directamente . El canal t representa el proceso en el que la partícula 1 emite la partícula intermedia y se convierte en la partícula final 3, mientras que la partícula 2 absorbe la partícula intermedia y se convierte en 4. El canal u es el canal t con el papel de las partículas 3,4 intercambiadas.

Al evaluar una amplitud de Feynman, a menudo se encuentran productos escalares de los cuatro momentos externos. Se pueden utilizar las variables de Mandelstam para simplificarlas:

p1⋅ ⋅ p2=s/c2− − m12− − m222{displaystyle p_{1}cdot P_{2}={frac {2}} {2}}}

p1⋅ ⋅ p3=m12+m32− − t/c22{displaystyle p_{1}cdot p_{3}={frac {m_{1} {2}+m_{3} {2}-t/c^{2}{2}}}}} {2}}}}}}

p1⋅ ⋅ p4=m12+m42− − u/c22{displaystyle p_{1}cdot p_{4}={frac {m_{1} {2}+m_{4} {2}-u/c^{2}{2}}}}}} {2}}}}}}

Donde mi{displaystyle m_{i} es la masa de la partícula con el impulso correspondiente pi{displaystyle P_{i}.

Suma

Tenga en cuenta que

()s+t+u)=()m12+m22+m32+m42)/c2{displaystyle (s+t+u)=(m_{1}{2}+m_{2}^{2}+m_{3}^{2}+m_{4}{2}/c^{2}}

donde m_i es la masa de la partícula i.

Límite relativo

En el límite relativista, el impulso (velocidad) es grande, por lo que utilizando la ecuación relativista de energía-momentum, la energía se convierte esencialmente en la norma del impulso (por ejemplo. E2=p⋅ ⋅ p+m02{displaystyle E^{2}=mathbf {p} cdot mathbf {p} ¿Qué? se convierte en E2. . p⋅ ⋅ p{displaystyle E^{2}approx {p} cdot mathbf {p}). La masa restante también puede ser descuidada.

Por ejemplo,

s/c2=()p1+p2)2=p12+p22+2p1⋅ ⋅ p2. . 2p1⋅ ⋅ p2{displaystyle s/c^{2}=(p_{1}+p_{2})^{2}=p_{2}+p_{2}{2}cdot p_{2}approx 2p_{1}cdot p_{2}

porque p12=m12{displaystyle ¿Qué? y p22=m22{displaystyle ¿Qué?.

Así,

s/c2. . {displaystyle s/c^{2}approx	2p1⋅ ⋅ p2. . {displaystyle 2p_{1}cdot p_{2}approx	2p3⋅ ⋅ p4{displaystyle 2p_{3}cdot p_{4}
t/c2. . {displaystyle t/c^{2}approx	− − 2p1⋅ ⋅ p3. . {displaystyle -2p_{1}cdot p_{3}approx	− − 2p2⋅ ⋅ p4{displaystyle -2p_{2}cdot p_{4}
u/c2. . {displaystyle u/c^{2}approx}	− − 2p1⋅ ⋅ p4. . {displaystyle -2p_{1}cdot p_{4}approx	− − 2p3⋅ ⋅ p2{displaystyle -2p_{3}cdot p_{2}