Valores predictivos positivos y negativos.

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En bioestadística, proporción de verdaderos resultados negativos positivos y verdaderos

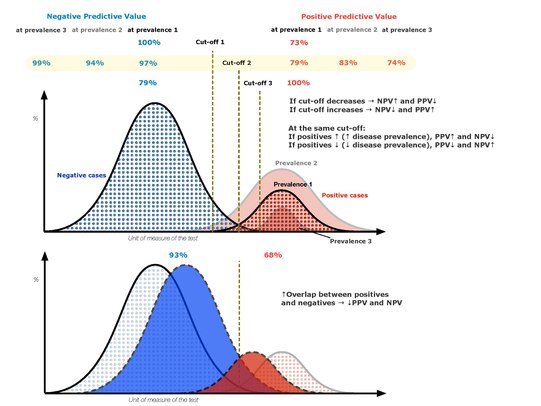
El valores predictivos positivos y negativos ()PPV y NPV respectivamente) son las proporciones de resultados positivos y negativos en estadísticas y pruebas de diagnóstico que son verdaderos resultados positivos y negativos verdaderos, respectivamente. El PPV y el NPV describen el rendimiento de una prueba de diagnóstico u otra medida estadística. Un resultado alto puede interpretarse como indicando la exactitud de tal estadística. El PPV y el NPV no son intrínsecos a la prueba (como la tasa positiva verdadera y la tasa negativa verdadera son); dependen también de la prevalencia. Tanto PPV como NPV pueden derivarse usando el teorema de Bayes.

Aunque a veces se utiliza como sinónimo, un valor predictivo positivo generalmente se refiere a lo establecido por los grupos de control, mientras que una probabilidad post-prueba se refiere a una probabilidad para un individuo. Aún así, si la probabilidad del individuo antes de la prueba de la condición objetivo es la misma que la prevalencia en el grupo de control utilizado para establecer el valor predictivo positivo, los dos son numéricamente iguales.

En la recuperación de información, la estadística PPV a menudo se denomina precisión.

Definición

Valor predictivo positivo (VPP)

El valor predictivo positivo (VPP), o precisión, se define como

{displaystyle {text{PPV}}={frac {text{Number of true positives}}{{text{Number of true positives}}+{text{Number of false positives}}}}={frac {text{Number of true positives}}{text{Number of positive calls}}}}

donde un "verdadero positivo" es el evento que la prueba hace una predicción positiva, y el sujeto tiene un resultado positivo bajo el estándar de oro, y un "falso positivo" es el evento que la prueba hace una predicción positiva, y el sujeto tiene un resultado negativo bajo el estándar de oro. El valor ideal del PPV, con una prueba perfecta, es 1 (100%), y el peor valor posible sería cero.

El VPP también se puede calcular a partir de la sensibilidad, la especificidad y la prevalencia de la afección:

{displaystyle {text{PPV}}={frac {{text{sensitivity}}times {text{prevalence}}}{{text{sensitivity}}times {text{prevalence}}+(1-{text{specificity}})times (1-{text{prevalence}})}}}

cf. Bayes' teorema

El complemento del PPV es la tasa de descubrimiento falso (FDR):

{displaystyle {text{FDR}}=1-{text{PPV}}={frac {text{Number of false positives}}{{text{Number of true positives}}+{text{Number of false positives}}}}={frac {text{Number of false positives}}{text{Number of positive calls}}}}

Valor predictivo negativo (VAN)

El valor predictivo negativo se define como:

{displaystyle {text{NPV}}={frac {text{Number of true negatives}}{{text{Number of true negatives}}+{text{Number of false negatives}}}}={frac {text{Number of true negatives}}{text{Number of negative calls}}}}

donde aparece un "verdadero negativo" es el evento en el que la prueba hace una predicción negativa, y el sujeto obtiene un resultado negativo según el estándar oro, y se produce un "falso negativo" es el caso de que la prueba haga una predicción negativa y el sujeto tenga un resultado positivo según el estándar oro. Con una prueba perfecta, aquella que no arroja falsos negativos, el valor del VPN es 1 (100%), y con una prueba que no arroja verdaderos negativos, el valor del VPN es cero.

El VPN también se puede calcular a partir de la sensibilidad, la especificidad y la prevalencia:

{displaystyle {text{NPV}}={frac {{text{specificity}}times (1-{text{prevalence}})}{{text{specificity}}times (1-{text{prevalence}})+(1-{text{sensitivity}})times {text{prevalence}}}}}

{displaystyle {text{NPV}}={frac {TN}{TN+FN}}}

El complemento del VAN es la tasa de falsas omisiones (PARA):

{displaystyle {text{FOR}}=1-{text{NPV}}={frac {text{Number of false negatives}}{{text{Number of true negatives}}+{text{Number of false negatives}}}}={frac {text{Number of false negatives}}{text{Number of negative calls}}}}

Aunque a veces se utiliza como sinónimo, un valor predictivo negativo generalmente se refiere a lo que establecen los grupos de control, mientras que una probabilidad post-prueba negativa se refiere más bien a una probabilidad para un individuo. Aún así, si la probabilidad del individuo antes de la prueba de la condición objetivo es la misma que la prevalencia en el grupo de control utilizado para establecer el valor predictivo negativo, entonces los dos son numéricamente iguales.

Relación

El siguiente diagrama ilustra cómo se relacionan el valor predictivo positivo, el valor predictivo negativo, la sensibilidad y la especificidad.

		Estado predecido		^Fuentes: ^{vista hablar edición}
	Población total $P + N$	Predicted Positive (PP)	Negativo predicho (PN)	Depósito, (BM) $TPR + TNR - 1$	umbral de prevalencia (PT) $= \sqrt TPR \times FPR - FPR / TPR - FPR$
Estado real	Positivo (P)	Verdaderamente positivo (TP), hit	Falso negativo (FN), error tipo II, señorita, subestimación	Tasa positiva verdadera (TPR), recuerdo, sensibilidad (SEN), probabilidad de detección, velocidad de impacto, potencia $= TP / P$ $1 - FNR$	Tasa negativa falsa (FNR), Tasa de pérdida $= FN / P$ $1 - RCP$
Estado real	Negativo (N)	Falso positivo (FP), error tipo I, falsa alarma, sobreestimación	Verdadero negativo (TN), rechazo correcto	Falsa tasa positiva (FPR), probabilidad de falsa alarma, caída $= FP / N$ $1 - RNR$	Tasa negativa verdadera (TNR), especificidad (SPC), selectividad $= TN / N$ $1 - FPR$
	Prevalencia $= P / P + N$	Valor predictivo positivo (PPV), precisión $= TP / PP$ $1 - FDR$	Tasa de omisión falsa (FOR) $= FN / PN$ $1 - VPH$	Tasa de probabilidad positiva (LR+) $= TPR / FPR$	Tasa de probabilidad negativa (LR−) $= FNR / TNR$
	Precisión (CAC) $= TP + TN / P + N$	Tasa falsa de descubrimiento (FDR) $= FP / PP$ $1 - PPV$	Valor predictivo negativo (NPV) $= TN / PN$ $1 - FOR$	Markedness (MK), deltaP (Δp) $PPV + NPV - 1$	Relación de probabilidades de diagnóstico (DOR) $= LR+ / LR -$
	Precisión equilibrada (BA) $= TPR + TNR / 2$	Puntaje F1 $= 2 PPV \times TPR / PPV + TPR$ $= 2 TP / 2 TP + FP + FN$	Fowlkes – Índice de los huecos (FM) $= \sqrt PPV \times TPR$	Coeficiente de correlación de Matthews (MCC) $= \sqrt TPR \times TNR \times PPV \times NPV$ $- \sqrt FNR \times FPR \times FDR$	Clasificación de amenazas (TS), índice de éxito crítico (CSI), índice de Jaccard $= TP / TP + FN + FP$

Tenga en cuenta que los valores predictivos positivos y negativos solo se pueden estimar utilizando datos de un estudio transversal u otro estudio poblacional en el que se puedan obtener estimaciones de prevalencia válidas. Por el contrario, la sensibilidad y la especificidad pueden estimarse a partir de estudios de casos y controles.

Ejemplo resuelto

Supongamos que la prueba de detección de sangre oculta en heces (FOB) se utiliza en 2030 personas para buscar cáncer de intestino:

		Resultado de prueba de sangre oculta fecal		^{vista hablar edición}
	Población total (pop.) = 2030	Resultado de los ensayos positivo	Resultado de los ensayos negativo	Precisión (CAC) = (TP + TN) / pop. = (20 + 1820) / 2030 . 90,64%	Puntaje F1 = 2 × precisión ×/precisión + memoria . 0.174
Pacientes con cáncer de intestino (como se confirmó sobre endoscopia)	Estado real positivo (AP) = 30 (2030 × 1.48%)	Verdadero positivo (TP) = 20 (2030 × 1.48% × 67%)	Falso negativo (FN) = 10 (2030 × 1.48% × (100% – 67%))	Tasa positiva verdadera (TPR), recuerdo, sensibilidad TP / AP = 20 / 30 . 66,7%	Tasa negativa falsa (FNR), tasa de pérdida FN / AP = 10 / 30 . 33.3%
	Estado real negativo (AN) 2000 (2030 × (100% – 1,48%))	Falso positivo (FP) = 180 (2030 × (100% – 1,48%) × (100% – 91%))	Verdadero negativo (TN) = 1820 (2030 × (100% – 1,48%) × 91%)	Falsa tasa positiva (FPR), caída, probabilidad de falsa alarma FP / AN = 180 / 2000 = 9.0%	Especificación, selectividad, verdadera tasa negativa (TNR) TN / AN = 1820 / 2000 = 91%
	Prevalencia = AP / pop. = 30 / 2030 . 1.48%	Valor predictivo positivo (PPV), precisión = TP / (TP + FP) = 20 / (20 + 180) = 10%	Tasa de omisión falsa (FOR) = FN / (FN + TN) = 10 / (10 + 1820) . 0,55%	Tasa de probabilidad positiva (LR+) = TPR/FPR = (20 / 30) / (180 / 2000) . 7.41	Tasa de probabilidad negativa (LR−) = FNR/TNR = (10 / 30) / (1820 / 2000) . 0.366
		Tasa falsa de descubrimiento (FDR) = FP / (TP + FP) = 180 / (20 + 180) = 90,0%	Valor predictivo negativo (NPV) = TN / (FN + TN) = 1820 / (10 + 1820) . 99,45%	Relación de probabilidades de diagnóstico (DOR) = LR+/LR - . 20.2

El pequeño valor predictivo positivo (VPP = 10%) indica que muchos de los resultados positivos de este procedimiento de prueba son falsos positivos. Por lo tanto, será necesario realizar un seguimiento de cualquier resultado positivo con una prueba más fiable para obtener una evaluación más precisa de la presencia de cáncer. Sin embargo, una prueba de este tipo puede resultar útil si es económica y conveniente. En cambio, la fortaleza de la prueba de detección FOB reside en su valor predictivo negativo, que, si es negativo para un individuo, nos da una alta confianza de que su resultado negativo es verdadero.

Problemas

Otros factores individuales

Tenga en cuenta que el VPP no es intrínseco a la prueba; también depende de la prevalencia. Debido al gran efecto de la prevalencia sobre los valores predictivos, se ha propuesto un enfoque estandarizado, donde el VPP se normaliza a una prevalencia del 50%. El VPP es directamente proporcional a la prevalencia de la enfermedad o afección. En el ejemplo anterior, si el grupo de personas examinadas hubiera incluido una mayor proporción de personas con cáncer de intestino, entonces el VPP probablemente sería mayor y el VPN menor. Si todos los miembros del grupo tuvieran cáncer de intestino, el VPP sería del 100 % y el VPN del 0 %.

Para superar este problema, el VPN y el PPV solo deben usarse si la relación entre el número de pacientes en el grupo de la enfermedad y el número de pacientes en el grupo de control sano utilizado para establecer el VPN y el PPV es equivalente a la prevalencia de las enfermedades en la población estudiada, o, en caso de que se comparen dos grupos de enfermedades, si la proporción entre el número de pacientes en el grupo de enfermedades 1 y el número de pacientes en el grupo de enfermedades 2 es equivalente a la proporción de las prevalencias de las dos enfermedades estudió. De lo contrario, los índices de probabilidad positivos y negativos son más precisos que el VPN y el VPP, porque los índices de probabilidad no dependen de la prevalencia.

Cuando un individuo sometido a la prueba tiene una probabilidad previa a la prueba diferente de tener una afección que los grupos de control utilizados para establecer el VPP y el VPN, el VPP y el VPN generalmente se distinguen de las probabilidades posteriores a la prueba positivas y negativas, con la El VPP y el VPN se refieren a los establecidos por los grupos de control, y las probabilidades post-test se refieren a las del individuo evaluado (estimadas, por ejemplo, mediante índices de verosimilitud). Preferiblemente, en tales casos, se debe estudiar un grupo grande de individuos equivalentes, con el fin de establecer valores predictivos positivos y negativos separados para el uso de la prueba en dichos individuos.

Actualización bayesiana

El teorema de Bayes confiere limitaciones inherentes a la exactitud de las pruebas de detección como función de prevalencia de enfermedades o probabilidad pre-prueba. Se ha demostrado que un sistema de pruebas puede tolerar caídas significativas en la prevalencia, hasta cierto punto bien definido conocido como el umbral de prevalencia, por debajo del cual la fiabilidad de una prueba de detección positiva disminuye precipitadamente. Eso dijo, Balayla et al. mostró que las pruebas secuenciales superan las limitaciones Bayesianas antes mencionadas y así mejora la fiabilidad de las pruebas de detección. Para un valor predictivo positivo deseado ${displaystyle rho }$ que se acerca a algo constante ${displaystyle k}$ , el número de iteraciones de prueba positivas ${displaystyle n_{i}}$ es necesario:

{displaystyle n_{i}=lim _{rho to k}leftlceil {frac {ln left[{frac {rho (phi -1)}{phi (rho -1)}}right]}{ln left[{frac {a}{1-b}}right]}}rightrceil }

dónde

${displaystyle rho }$ es el PPV deseado
${displaystyle n_{i}}$ es el número de pruebas iteraciones necesarias para lograr ${displaystyle rho }$
${displaystyle a}$ es la sensibilidad
${displaystyle b}$ es la especificidad
${displaystyle phi }$ es la prevalencia de enfermedades, y
${displaystyle k}$ es una constante.

Cabe destacar que el denominador de la ecuación anterior es el logaritmo natural de la razón de verosimilitud positiva (LR+).

Diferentes condiciones de destino

El VPP se utiliza para indicar la probabilidad de que, en caso de una prueba positiva, el paciente realmente tenga la enfermedad especificada. Sin embargo, puede haber más de una causa para una enfermedad y es posible que una sola causa potencial no siempre dé como resultado la enfermedad manifiesta que se observa en un paciente. Existe la posibilidad de mezclar condiciones objetivo relacionadas de PPV y VPN, como interpretar el PPV o VPN de una prueba como si tuviera una enfermedad, cuando ese valor de PPV o VPN en realidad se refiere solo a una predisposición a tener esa enfermedad.

Un ejemplo es el hisopo microbiológico de garganta que se utiliza en pacientes con dolor de garganta. Por lo general, las publicaciones que indican el VPP de un hisopo de garganta informan sobre la probabilidad de que esta bacteria esté presente en la garganta, en lugar de que el paciente esté enfermo a causa de la bacteria encontrada. Si la presencia de esta bacteria siempre provocara dolor de garganta, entonces la VPP sería muy útil. Sin embargo, las bacterias pueden colonizar a las personas de forma inofensiva y nunca provocar infecciones o enfermedades. Los dolores de garganta que ocurren en estas personas son causados por otros agentes, como un virus. En esta situación, el estándar de oro utilizado en el estudio de evaluación representa sólo la presencia de bacterias (que podrían ser inofensivas), pero no una enfermedad bacteriana causal de dolor de garganta. Se puede demostrar que este problema afectará el valor predictivo positivo mucho más que el valor predictivo negativo. Para evaluar pruebas de diagnóstico en las que el estándar de oro sólo analiza las causas potenciales de la enfermedad, se puede utilizar una extensión del valor predictivo denominada valor predictivo etiológico.

Contenido relacionado

Más resultados...