Valor singular de descomposición

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Matrix decomposition

Ilustración de la descomposición de valor singular U ElisabethV^⁎ de una matriz 2×2 real M.

Top: La acción de M, indicado por su efecto en el disco de unidad D y los dos vectores de unidad canónica e₁ y e₂.
Izquierda: La acción de V^⁎, una rotación, en D, e₁, y e₂.
Tema: La acción de ., un escalado por los valores singulares σ₁ horizontal y σ₂ verticalmente.
Bien. La acción de UOtra rotación.

En álgebra lineal, el singular valor descomposición ()SVD) es una factorización de una matriz real o compleja. Generaliza la eigendecomposición de una matriz normal cuadrada con una eigenbasis ortonormal a cualquier ${displaystyle mtimes n }$ matriz. Está relacionado con la descomposición polar.

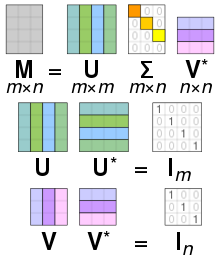
Específicamente, la descomposición de valor singular de ${displaystyle mtimes n }$ matriz compleja $M$ es una factorización de la forma ${displaystyle mathbf {M} =mathbf {USigma V^{*}} }$ Donde $U$ es un ${displaystyle mtimes m }$ compleja matriz unitaria, ${displaystyle mathbf {Sigma } }$ es un ${displaystyle mtimes n }$ matriz diagonal rectangular con números reales no negativos en el diagonal, $V$ es un $ntimes n$ compleja matriz unitaria, y ${displaystyle mathbf {V^{*}} }$ es la transposición conyugal $V$ . Tal descomposición siempre existe para cualquier matriz compleja. Si $M$ es real, entonces $U$ y $V$ puede ser garantizado para ser matrices ortogonales reales; en tales contextos, el SVD es a menudo denotado ${displaystyle mathbf {USigma V} ^{mathsf {T}}.}$

Las entradas diagonales ${displaystyle sigma _{i}=Sigma _{ii} }$ de ${displaystyle mathbf {Sigma } }$ están determinados por $M$ y son conocidos como los valores singulares $M$ . El número de valores no individuales es igual al rango de $M$ . Las columnas de $U$ y las columnas de $V$ son llamados vectores de izquierda-singular y vectores de derecha-singular de $M$ , respectivamente. Forman dos conjuntos de bases ortonormales $u 1,... u m$ y $v 1,... v n$ , y si están ordenados para que los valores singulares ${displaystyle sigma _{i} }$ con valor cero están todos en las columnas más numeradas (o filas), la descomposición de valor singular se puede escribir como ${displaystyle mathbf {M} =sum _{i=1}^{r}sigma _{i}mathbf {u} _{i}mathbf {v} _{i}^{*}}$ Donde ${displaystyle rleq min{m,n} }$ es el rango de $M$ .

El SVD no es único. Siempre es posible elegir la descomposición para que los valores singulares ${displaystyle Sigma _{ii}}$ están en orden descendente. En este caso, $mathbf{Sigma}$ (pero no $U$ y $V$ ) es determinado por $M$ .

El término a veces se refiere a compacto SVD, una descomposición similar ${displaystyle mathbf {M} =mathbf {USigma V^{*}} }$ en que ${displaystyle mathbf {Sigma } }$ es diagonal cuadrado de tamaño $r times r$ , donde ${displaystyle rleq min{m,n} }$ es el rango de $M$ , y tiene sólo los valores no cero singulares. En esta variante, $U$ es un $mtimes r$ matriz semiunitaria y ${displaystyle mathbf {V} }$ es un $ntimes r$ matriz semiunitaria, tal que ${displaystyle mathbf {U^{*}U} =mathbf {V^{*}V} =mathbf {I} _{r}.}$

Las aplicaciones matemáticas del SVD incluyen el cálculo de la pseudoinversa, la aproximación de matrices y la determinación del rango, el rango y el espacio nulo de una matriz. El SVD también es extremadamente útil en todas las áreas de la ciencia, la ingeniería y las estadísticas, como el procesamiento de señales, el ajuste de datos por mínimos cuadrados y el control de procesos.

Interpretaciones intuitivas

Ilustración animada del SVD de una matriz de corte real 2D

M

. En primer lugar, vemos el disco de unidad en azul junto con los dos vectores de unidad canónica. Entonces vemos las acciones

M

, que distorsiona el disco a una elipse. El SVD se descompone

M

en tres transformaciones simples: una rotación inicial

V ⁎

, una escalada

mathbf{Sigma}

a lo largo de los ejes de coordenadas, y una rotación final

U

. Las longitudes

σ 1

σ 2

de los semi-axies de la elipse son los valores singulares de

M

, a saber

. 1.1

. 2,2

Visualización de las multiplicaciones de matriz en descomposición de valor singular

Rotación, escalado de coordenadas y reflexión

En el caso especial cuando $M$ es un $m \times m$ matriz cuadrada real, las matrices $U$ y $V ⁎$ puede ser elegido para ser real $m \times m$ Las matrices también. En ese caso, "uniario" es el mismo que "ortogonal". Luego, interpretando tanto matrices unitarias como la matriz diagonal, resumido aquí como $A$ , como una transformación lineal $x \mapsto Ax$ del espacio $R m$ , las matrices $U$ y $V ⁎$ representan rotaciones o reflexión del espacio, mientras $mathbf{Sigma}$ representa el escalado de cada coordenadas $x i$ por el factor $σ i$ . Así la descomposición SVD descompone cualquier transformación lineal $R m$ en una composición de tres transformaciones geométricas: una rotación o reflexión ( $V ⁎$ ), seguido de un escalado coordinado ( $mathbf{Sigma}$ ), seguido de otra rotación o reflexión ( $U$ ).

En particular, si $M$ tiene un determinante positivo, entonces $U$ y $V ⁎$ se pueden elegir para que sean ambas rotaciones con reflejos o ambas rotaciones sin reflejos. Si el determinante es negativo, exactamente uno de ellos tendrá un reflejo. Si el determinante es cero, cada uno puede elegirse independientemente para que sea de cualquier tipo.

Si la matriz $M$ es real pero no cuadrada, $m \times n$ con $m ل n$ , se puede interpretar como una transformación lineal de $R n$ a $R m$ . Entonces... $U$ y $V ⁎$ puede ser elegido para ser rotaciones/reflexiones de $R m$ y $R n$ , respectivamente; y $mathbf{Sigma}$ , además de escalar el primero $min{m,n}$ coordenadas, también extiende el vector con ceros, es decir, elimina las coordenadas de seguimiento, para girar $R n$ en $R m$ .

Valores singulares como semiejes de una elipse o elipsoide

Como se muestra en la figura, los valores singulares se pueden interpretar como la magnitud de los semiejes de una elipse en 2D. Este concepto se puede generalizar al espacio euclidiano de $n$ -dimensionales, con los valores singulares de cualquier $n \times n$ matriz cuadrada vista como la magnitud del semieje de una $n$ -dimensional. De manera similar, los valores singulares de cualquier matriz $m \times n$ pueden verse como la magnitud del semieje de una $n$ -elipsoide dimensional en $m$ -espacio dimensional, por ejemplo como una elipse en un plano 2D (inclinado) en un espacio 3D. Los valores singulares codifican la magnitud del semieje, mientras que los vectores singulares codifican la dirección. Consulte a continuación para obtener más detalles.

Las columnas de U y V son bases ortonormales

Desde $U$ y $V ⁎$ son unitarios, las columnas de cada uno de ellos forman un conjunto de vectores ortonormales, que pueden considerarse vectores de base. La matriz $M$ mapas la base vector $V i$ al vector de unidad estirada $σ i U i$ . Por la definición de una matriz unitaria, lo mismo es cierto para sus transposos conjugados $U ⁎$ y $V$ , excepto la interpretación geométrica de los valores singulares como estiramientos se pierde. En resumen, las columnas de $U, U ⁎, V$ , y $V ⁎$ son bases ortonormales. Cuando $mathbf {M}$ es una matriz hermitiana positiva, $U$ y $V$ ambos son iguales a la matriz unitaria utilizada para diagonalizar $mathbf {M}$ . Sin embargo, cuando $mathbf {M}$ no es positivo-semidefinito y Hermitian pero todavía diagonalizable, su eigendecomposición y descomposición de valor singular son distintos.

Significado geométrico

Debido a que $U$ y $V$ son unitarios, sabemos que las columnas $U 1,..., U m$ de $U$ produce una base ortonormal de $K m$ y las columnas $V 1,..., V n$ de $V$ producen una ortonormal base de $K n$ (con respecto a los productos escalares estándar en estos espacios).

La transformación lineal

{displaystyle Tcolon left{{begin{aligned}K^{n}&to K^{m}\x&mapsto mathbf {M} xend{aligned}}right.}

tiene una descripción particularmente simple con respecto a estas bases ortonormales: tenemos

{displaystyle T(mathbf {V} _{i})=sigma _{i}mathbf {U} _{i},qquad i=1,ldotsmin(m,n),}

Donde $σ i$ es $i$ -la entrada diagonal $mathbf{Sigma}$ , y $T () V i) = 0$ para $i Ø min(m, n)$ .

El contenido geométrico del teorema SVD se puede resumir así: para todo mapa lineal $T : K n \to K m$ uno puede encontrar bases ortonormales de $K n$ y $K m$ tales que $T$ mapea el $i$ -th vector base de $K n$ a un múltiplo no negativo de $i$ -ésimo vector base de $K m$ , y envía los vectores base sobrantes a cero. Con respecto a estas bases, el mapa $T$ se representa por tanto mediante una matriz diagonal con entradas diagonales reales no negativas.

Para obtener una idea más visual de los valores singulares y la factorización SVD, al menos cuando se trabaja en espacios vectoriales reales, considere la esfera $S$ de radio uno en $R n$ . El mapa lineal $T$ asigna esta esfera a un elipsoide en $R m$ . Los valores singulares distintos de cero son simplemente las longitudes de los semiejes de este elipsoide. Especialmente cuando $n = m$ , y todos los valores singulares son distintos y distintos de cero, el SVD del mapa lineal $T$ se puede analizar fácilmente como una sucesión de tres movimientos consecutivos: considere el elipsoide $T (S)$ y específicamente sus ejes; luego considere las instrucciones en $R n$ enviadas por $T$ en estos ejes. Estas direcciones resultan ser mutuamente ortogonales. Aplique primero una isometría $V ⁎$ enviando estas direcciones a los ejes de coordenadas de $R n$ . En un segundo movimiento, aplique un endomorfismo $D$ diagonalizado a lo largo de los ejes de coordenadas y alargando o encogiendo en cada dirección, usando las longitudes de los semiejes de $T (S)$ como coeficientes de estiramiento. La composición $D \circ V ⁎$ luego envía la esfera unitaria a un elipsoide isométrico para $T (S)$ . Para definir el tercer y último movimiento, aplique una isometría $U$ a este elipsoide para obtener $T (S)$ . Como se puede comprobar fácilmente, la composición $U \circ D \circ V ⁎$ coincide con $T$ .

Ejemplo

Considere la matriz $4 \times 5$

mathbf {M} ={begin{bmatrix}1&0&0&0&2\0&0&3&0&0\0&0&0&0&0\0&2&0&0&0end{bmatrix}}

Una descomposición en valores singulares de esta matriz viene dada por $UΣV ⁎$

{displaystyle {begin{aligned}mathbf {U} &={begin{bmatrix}color {Green}0&color {Blue}-1&color {Cyan}0&color {Emerald}0\color {Green}-1&color {Blue}0&color {Cyan}0&color {Emerald}0\color {Green}0&color {Blue}0&color {Cyan}0&color {Emerald}-1\color {Green}0&color {Blue}0&color {Cyan}-1&color {Emerald}0end{bmatrix}}\[6pt]{boldsymbol {Sigma }}&={begin{bmatrix}3&0&0&0&color {Gray}{mathit {0}}\0&{sqrt {5}}&0&0&color {Gray}{mathit {0}}\0&0&2&0&color {Gray}{mathit {0}}\0&0&0&color {Red}mathbf {0} &color {Gray}{mathit {0}}end{bmatrix}}\[6pt]mathbf {V} ^{*}&={begin{bmatrix}color {Violet}0&color {Violet}0&color {Violet}-1&color {Violet}0&color {Violet}0\color {Plum}-{sqrt {0.2}}&color {Plum}0&color {Plum}0&color {Plum}0&color {Plum}-{sqrt {0.8}}\color {Magenta}0&color {Magenta}-1&color {Magenta}0&color {Magenta}0&color {Magenta}0\color {Orchid}0&color {Orchid}0&color {Orchid}0&color {Orchid}1&color {Orchid}0\color {Purple}-{sqrt {0.8}}&color {Purple}0&color {Purple}0&color {Purple}0&color {Purple}{sqrt {0.2}}end{bmatrix}}end{aligned}}}

La matriz de escalado $mathbf{Sigma}$ es cero fuera de la diagonal (variedad gris) y un elemento diagonal es cero (rojo negrita, azul claro audaz en modo oscuro). Además, porque las matrices $U$ y $V ⁎$ son unitarios, multiplicando por sus respectivos transpos conjugados produce matrices de identidad, como se muestra a continuación. En este caso, porque $U$ y $V ⁎$ son valorados reales, cada una es una matriz ortogonal.

{displaystyle {begin{aligned}mathbf {U} mathbf {U} ^{*}&={begin{bmatrix}1&0&0&0\0&1&0&0\0&0&1&0\0&0&0&1end{bmatrix}}=mathbf {I} _{4}\[6pt]mathbf {V} mathbf {V} ^{*}&={begin{bmatrix}1&0&0&0&0\0&1&0&0&0\0&0&1&0&0\0&0&0&1&0\0&0&0&0&1end{bmatrix}}=mathbf {I} _{5}end{aligned}}}

Esta descomposición de valor particular no es única. Elegir ${mathbf V}$ tales que

{displaystyle mathbf {V} ^{*}={begin{bmatrix}color {Violet}0&color {Violet}1&color {Violet}0&color {Violet}0&color {Violet}0\color {Plum}0&color {Plum}0&color {Plum}1&color {Plum}0&color {Plum}0\color {Magenta}{sqrt {0.2}}&color {Magenta}0&color {Magenta}0&color {Magenta}0&color {Magenta}{sqrt {0.8}}\color {Orchid}{sqrt {0.4}}&color {Orchid}0&color {Orchid}0&color {Orchid}{sqrt {0.5}}&color {Orchid}-{sqrt {0.1}}\color {Purple}-{sqrt {0.4}}&color {Purple}0&color {Purple}0&color {Purple}{sqrt {0.5}}&color {Purple}{sqrt {0.1}}end{bmatrix}}}

también es una descomposición de valor singular válida.

SVD y descomposición espectral

Valores singulares, vectores singulares y su relación con el SVD

Un número real no negativo $σ$ es un Valor singular para $M$ si y sólo si existen vectores de longitud unitaria $mathbf {u}$ dentro K^m y $mathbf {v}$ dentro Kⁿ tales que

{displaystyle mathbf {Mv} =sigma mathbf {u} ,{text{ and }}mathbf {M} ^{*}mathbf {u} =sigma mathbf {v}.}

Los vectores $mathbf {u}$ y $mathbf {v}$ se llaman izquierda-singular y vectores de derecha-singular para $σ$ , respectivamente.

En cualquier descomposición de valores singulares

mathbf {M} =mathbf {U} {boldsymbol {Sigma }}mathbf {V} ^{*}

las entradas diagonales de $mathbf{Sigma}$ son iguales a los valores singulares $M$ . La primera $p = min(m, n)$ columnas de $U$ y $V$ son, respectivamente, vectores de izquierda y derecha-singular para los valores singulares correspondientes. En consecuencia, el teorema anterior implica que:

An $m \times n$ matriz $M$ tiene $p$ valores singulares distintos.
Siempre es posible encontrar una base unitaria $U$ para $K m$ con un subconjunto de vectores de base que abarcan los vectores izquierdistas de cada valor singular de $M$ .
Siempre es posible encontrar una base unitaria $V$ para $K n$ con un subconjunto de vectores de base que abarcan los vectores de derecha-singulares de cada valor singular de $M$ .

Un valor singular para el cual podemos encontrar dos vectores singulares izquierda (o derecha) que son linealmente independientes se llama degenerado. Si ${mathbf {u}}_{1}$ y ${displaystyle mathbf {u} _{2}}$ son dos vectores izquierdistas que ambos corresponden al valor singular σ, entonces cualquier combinación lineal normalizada de los dos vectores es también un vector izquierdista correspondiente al valor singular σ. La declaración similar es verdadera para los vectores de derecha-singular. El número de vectores independientes de izquierda y derecha-singular coincide, y estos vectores singulares aparecen en las mismas columnas de $U$ y $V$ correspondiente a elementos diagonales $mathbf{Sigma}$ todos con el mismo valor σ.

Como excepción, los vectores singulares izquierdo y derecho de valor singular 0 comprenden todos los vectores unitarios en el cokernel y el kernel, respectivamente, de $M$ , que por el teorema de rango-nulidad no puede tener la misma dimensión si $m \neq n$ . Incluso si todos los valores singulares son distintos de cero, si $m > n$ entonces el cokernel no es trivial, en cuyo caso $U$ se rellena con $m - n$ vectores ortogonales del cokernel. Por el contrario, si $m < n$ , luego $V$ se rellena con $n - m$ vectores ortogonales del núcleo. Sin embargo, si existe el valor singular de 0, las columnas adicionales de $U$ o $V$ ya aparecen como vectores singulares izquierdo o derecho.

Los valores singulares no degenerados siempre tienen vectores singulares izquierdo y derecho únicos, hasta la multiplicación por un factor de fase unitaria e^{i φ} (para el caso real hasta una señal). En consecuencia, si todos los valores singulares de una matriz cuadrada $M$ son no degenerados y distintos de cero, entonces su descomposición de valor singular es única, hasta la multiplicación de una columna de $U$ por un factor de fase unitaria y multiplicación simultánea de la columna correspondiente de $V$ por el mismo factor de unidad de fase. En general, el SVD es único hasta transformaciones unitarias arbitrarias aplicadas uniformemente a los vectores de columna de $U$ y $V$ que abarca los subespacios de cada valor singular, y hasta transformaciones unitarias arbitrarias en vectores de $U$ y $V$ que abarca el kernel y el cokernel, respectivamente, de $M$ .

Relación con la descomposición de valores propios

La descomposición en valores singulares es muy general en el sentido de que se puede aplicar a cualquier matriz $m \times n$ , mientras que la descomposición de valores propios solo se puede aplicar a matrices diagonalizables. Sin embargo, las dos descomposiciones están relacionadas.

Dado un SVD de $M$ , como se describe arriba, se cumplen las siguientes dos relaciones:

{begin{aligned}mathbf {M} ^{*}mathbf {M} &=mathbf {V} {boldsymbol {Sigma }}^{*}mathbf {U} ^{*},mathbf {U} {boldsymbol {Sigma }}mathbf {V} ^{*}=mathbf {V} ({boldsymbol {Sigma }}^{*}{boldsymbol {Sigma }})mathbf {V} ^{*}\mathbf {M} mathbf {M} ^{*}&=mathbf {U} {boldsymbol {Sigma }}mathbf {V} ^{*},mathbf {V} {boldsymbol {Sigma }}^{*}mathbf {U} ^{*}=mathbf {U} ({boldsymbol {Sigma }}{boldsymbol {Sigma }}^{*})mathbf {U} ^{*}end{aligned}}

Los lados derechos de estas relaciones describen las descomposiciones de valores propios de los lados izquierdos. Como consecuencia:

Las columnas de $V$ (vectores fijos) son eigenvectores de $M ⁎ M$ .
Las columnas de $U$ (left-singular vectores) son eigenvectores de $MM ⁎$ .
Los elementos no cero de $mathbf{Sigma}$ (valores no cero singulares) son las raíces cuadradas de los valores no cero de los $M ⁎ M$ o $MM ⁎$ .

En el caso especial de que $M$ sea una matriz normal, que por definición debe ser cuadrada, el teorema espectral dice que se puede diagonalizar unitariamente utilizando una base de vectores propios, de modo que se puede escribir $M = UDU ⁎$ para una matriz unitaria $U$ y una matriz diagonal $D$ con elementos complejos $σ i$ a lo largo de la diagonal. Cuando $M$ es positivo semidefinido, $σ i$ serán números reales no negativos para que la descomposición $M = UDU ⁎$ también es una descomposición de valores singulares. De lo contrario, se puede reformular como SVD moviendo la fase $e iφ$ de cada $σ i$ a su correspondiente $V i$ o $U i$ . La conexión natural de la SVD con matrices no normales es a través del teorema de descomposición polar: $M = SR$ , donde $S = UΣU ⁎$ es semidefinido positivo y normal, y $R = UV ⁎$ es unitario.

Así, excepto las matrices semidefinidas positivas, la descomposición eigenvalue y el SVD de $M$ , mientras está relacionado, difieren: la descomposición de eigenvalue es $M = UDU -1$ , donde $U$ no es necesariamente unitario y $D$ no es necesariamente positivo semi-definido, mientras que el SVD es $M = U ElisabethV ⁎$ , donde $mathbf{Sigma}$ es diagonal y positivo semi-definido, y $U$ y $V$ son matrices unitarias que no están necesariamente relacionadas excepto a través de la matriz $M$ . Aunque sólo las matrices cuadradas no defectuosas tienen una descomposición de valor eigen, cualquier $mtimes n$ matriz tiene un SVD.

Aplicaciones de la SVD

Pseudoinversa

La descomposición en valores singulares se puede utilizar para calcular la pseudoinversa de una matriz. (Varios autores usan una notación diferente para la pseudoinversa; aquí usamos $†$ ). De hecho, la pseudoinversa de la matriz $M$ con descomposición en valores singulares $M = UΣV ⁎$ es

M † = V . † U ⁎

donde $Σ †$ es el pseudoinverso de $Σ$ , que se forma reemplazando cada entrada diagonal distinta de cero por su recíproco y transponiendo la matriz resultante. La pseudoinversa es una forma de resolver problemas de mínimos cuadrados lineales.

Resolver ecuaciones lineales homogéneas

Un conjunto de ecuaciones lineales homogéneas se puede escribir como $Ax = 0$ para una matriz $A$ y el vector $x$ . Una situación típica es que se conoce $A$ y $x$ se va a determinar cuál satisface la ecuación. Tal $x$ pertenece a $A$ 's nulo space y a veces se le llama vector nulo (derecho) de $A$ . El vector $x$ se puede caracterizar como un vector singular derecho correspondiente a un valor singular de $A$ que es cero. Esta observación significa que si $A$ es una matriz cuadrada y no tiene un valor singular que se desvanece, la ecuación no tiene ningún $x$ como solución. También significa que si hay varios valores singulares que desaparecen, cualquier combinación lineal de los vectores singulares rectos correspondientes es una solución válida. Análogamente a la definición de un vector nulo (derecho), un $x$ distinto de cero que satisface $x ⁎ A = 0$ , con $x ⁎$ que denota la transposición conjugada de $x$ , se denomina vector nulo izquierdo de $A$ .

Minimización de mínimos cuadrados totales

Un problema de mínimos cuadrados totales busca el vector $x$ que minimiza la norma 2 de un vector $Ax$ bajo la restricción $|| x || = 1$ . La solución resulta ser el vector singular derecho de $A$ correspondiente al valor singular más pequeño.

Rango, espacio nulo y rango

Otra aplicación del SVD es que proporciona una representación explícita del rango y el espacio nulo de una matriz $M$ . Los vectores singulares a la derecha correspondientes a los valores singulares que desaparecen de $M$ abarcan el espacio nulo de $M$ y los vectores singulares a la izquierda correspondientes a los valores singulares distintos de cero de $M$ abarcan el rango de M. Por ejemplo, en el ejemplo anterior, el espacio nulo está dividido por las dos últimas filas de $V ⁎$ y el rango es abarcado por las tres primeras columnas de $U$ .

Como consecuencia, el rango de $M$ igual al número de valores no singulares cero que es el mismo que el número de elementos diagonales no cero en $mathbf{Sigma}$ . En álgebra lineal numérica los valores singulares se pueden utilizar para determinar rango efectivo de una matriz, ya que el error de redondeo puede llevar a valores pequeños pero no cero singulares en una matriz deficiente de rango. Se supone que los valores singulares más allá de una brecha significativa equivalen numéricamente a cero.

Aproximación de matriz de rango bajo

Algunas aplicaciones prácticas necesitan resolver el problema de aproximar una matriz $M$ con otra matriz ${tilde {mathbf {M} }}$ , dijo ser truncado, que tiene un rango específico $r$ . En el caso de que la aproximación se base en minimizar la norma Frobenius de la diferencia entre $M$ y ${tilde {mathbf {M} }}$ en virtud de la limitación $operatorname {rank} left({tilde {mathbf {M} }}right)=r$ , resulta que la solución es dada por el SVD de $M$ , a saber

{displaystyle {tilde {mathbf {M} }}=mathbf {U} {tilde {boldsymbol {Sigma }}}mathbf {V} ^{*},}

Donde ${tilde {boldsymbol {Sigma }}}$ es la misma matriz $mathbf{Sigma}$ excepto que contiene sólo $r$ valores singulares más grandes (los otros valores singulares son reemplazados por cero). Esto es conocido como Eckart-Young theorem, como fue probado por esos dos autores en 1936 (aunque se descubrió que posteriormente se conocía a autores anteriores; véase Stewart 1993).

Modelos separables

El SVD puede ser pensado como descomponer una matriz en una suma ponderada y ordenada de matrices separables. Por separado, queremos decir que una matriz $A$ puede ser escrito como un producto exterior de dos vectores $A = u \otimes v$ , o, en coordenadas, $A_{ij}=u_{i}v_{j}$ . Específicamente, la matriz $M$ puede ser descompuesto

{displaystyle mathbf {M} =sum _{i}mathbf {A} _{i}=sum _{i}sigma _{i}mathbf {U} _{i}otimes mathbf {V} _{i}.}

Aquí $U i$ y $V i$ son las $i$ -ésimas columnas de las matrices SVD correspondientes, $σ i$ son los valores singulares ordenados, y cada $A i$ es separable. El SVD se puede utilizar para encontrar la descomposición de un filtro de procesamiento de imágenes en filtros horizontales y verticales separables. Tenga en cuenta que el número de $σ i$ distintos de cero es exactamente el rango de la matriz.

Los modelos separables a menudo surgen en los sistemas biológicos, y la factorización SVD es útil para analizar tales sistemas. Por ejemplo, algunas celdas simples del área visual V1' los campos receptivos pueden describirse bien mediante un filtro Gabor en el dominio del espacio multiplicado por una función de modulación en el dominio del tiempo. Por lo tanto, dado un filtro lineal evaluado a través de, por ejemplo, correlación inversa, se pueden reorganizar las dos dimensiones espaciales en una dimensión, produciendo así un filtro bidimensional (espacio, tiempo) que se puede descomponer a través de SVD. La primera columna de $U$ en la factorización SVD es entonces un Gabor mientras que la primera columna de $V$ representa la modulación del tiempo (o viceversa). Entonces se puede definir un índice de separabilidad

alpha ={frac {sigma _{1}^{2}}{sum _{i}sigma _{i}^{2}}},

que es la fracción de la potencia en la matriz M que se explica por la primera matriz separable en la descomposición.

Matriz ortogonal más cercana

Es posible utilizar el SVD de una matriz cuadrada $A$ para determinar la matriz ortogonal $O$ más cercano a $A$ . La proximidad del ajuste se mide por la norma de Frobenius de $O - A$ . La solución es el producto $UV ⁎$ . Esto intuitivamente tiene sentido porque una matriz ortogonal tendría la descomposición $UIV ⁎$ donde $I$ es la matriz identidad, de modo que si $A = UΣV ⁎$ entonces el producto $A = UV ⁎$ equivale a reemplazar el valores singulares con unos. De manera equivalente, la solución es la matriz unitaria $R = UV ⁎$ de la Descomposición Polar $M = RP = P' R$ en cualquier orden de estiramiento y rotación, como se describe anteriormente.

Un problema similar, con aplicaciones interesantes en el análisis de formas, es el problema de Procrustes ortogonal, que consiste en encontrar una matriz ortogonal $O$ que más se aproxime asigna $A$ a $B$ . Específicamente,

{displaystyle mathbf {O} ={underset {Omega }{operatorname {argmin} }}|mathbf {A} {boldsymbol {Omega }}-mathbf {B} |_{F}quad {text{subject to}}quad {boldsymbol {Omega }}^{textsf {T}}{boldsymbol {Omega }}=mathbf {I}}

Donde $|cdot |_{F}$ denota la norma Frobenius.

Este problema es equivalente a encontrar la matriz ortogonal más cercana a una matriz dada $M = A T B$ .

El algoritmo de Kabsch

El algoritmo de Kabsch (llamado problema de Wahba en otros campos) usa SVD para calcular la rotación óptima (con respecto a la minimización de mínimos cuadrados) que alineará un conjunto de puntos con un conjunto de puntos correspondiente. Se utiliza, entre otras aplicaciones, para comparar las estructuras de las moléculas.

Procesamiento de señales

La SVD y la pseudoinversa se han aplicado con éxito al procesamiento de señales, procesamiento de imágenes y big data (por ejemplo, en el procesamiento de señales genómicas).

Astrodinámica

En astrodinámica, el SVD y sus variantes se utilizan como una opción para determinar las direcciones de maniobra adecuadas para el diseño de trayectorias de transferencia y el mantenimiento de la posición orbital.

Otros ejemplos

El SVD también se aplica ampliamente al estudio de problemas lineales inversos y es útil en el análisis de métodos de regularización como el de Tikhonov. Es ampliamente utilizado en estadística, donde se relaciona con el análisis de componentes principales y el análisis de correspondencias, y en el procesamiento de señales y el reconocimiento de patrones. También se utiliza en el análisis modal de solo salida, donde las formas de modo no escaladas se pueden determinar a partir de los vectores singulares. Otro uso más es la indexación semántica latente en el procesamiento de texto en lenguaje natural.

En general, la computación numérica que implica sistemas lineales o linealizados, existe una constante universal que caracteriza la regularidad o singularidad de un problema, que es el "número de condición" del sistema ${displaystyle kappa:=sigma _{text{max}}/sigma _{text{min}}}$ . A menudo controla la tasa de error o la tasa de convergencia de un determinado esquema computacional en dichos sistemas.

El SVD también desempeña un papel crucial en el campo de la información cuántica, en un formulario a menudo denominado descomposición Schmidt. A través de ella, los estados de dos sistemas cuánticos están naturalmente descompuestos, proporcionando una condición necesaria y suficiente para que sean enredados: si el rango de la $mathbf{Sigma}$ matriz es mayor que una.

Una aplicación de SVD a matrices bastante grandes es en la predicción meteorológica numérica, donde los métodos de Lanczos se utilizan para estimar las pocas perturbaciones de crecimiento más lineal y rápido en la predicción meteorológica numérica central durante un período de tiempo inicial dado; es decir, los vectores singulares correspondientes a los valores singulares más grandes del propagador linealizado para el clima global durante ese intervalo de tiempo. Los vectores singulares de salida en este caso son sistemas meteorológicos completos. Luego, estas perturbaciones se ejecutan a través del modelo no lineal completo para generar un pronóstico de conjunto, lo que permite controlar parte de la incertidumbre que debe permitirse en torno a la predicción central actual.

SVD también se ha aplicado al modelado de orden reducido. El objetivo del modelado de orden reducido es reducir el número de grados de libertad en un sistema complejo que se va a modelar. SVD se combinó con funciones de base radial para interpolar soluciones a problemas tridimensionales de flujo no estacionario.

Curiosamente, SVD se ha utilizado para mejorar el modelado de formas de ondas gravitacionales mediante el interferómetro de ondas gravitacionales basado en tierra aLIGO. SVD puede ayudar a aumentar la precisión y la velocidad de la generación de formas de onda para respaldar las búsquedas de ondas gravitacionales y actualizar dos modelos de formas de onda diferentes.

La descomposición de valores singulares se utiliza en los sistemas de recomendación para predecir las calificaciones de elementos de las personas. Se han desarrollado algoritmos distribuidos con el fin de calcular el SVD en grupos de máquinas comerciales.

Se ha aplicado SVD de rango bajo para la detección de puntos críticos a partir de datos espaciotemporales con aplicación a la detección de brotes de enfermedades. También se ha aplicado una combinación de SVD y SVD de orden superior para la detección de eventos en tiempo real a partir de flujos de datos complejos (datos multivariados con dimensiones de espacio y tiempo) en la vigilancia de enfermedades.

Prueba de existencia

Un valor propio $λ$ de una matriz $M$ se caracteriza por la relación algebraica $Mu = λ u$ . Cuando $M$ es hermitiano, también está disponible una caracterización variacional. Sea $M$ un $n \times n matriz simétrica. Definir$

{displaystyle {begin{cases}f:mathbb {R} ^{n}to mathbb {R} \f:mathbf {x} mapsto mathbf {x} ^{textsf {T}}mathbf {M} mathbf {x} end{cases}}}

Por el teorema del valor extremo, esta función continua alcanza un máximo en alguna u cuando se restringe a la esfera unitaria {||x|| = 1}. Por el teorema de los multiplicadores de Lagrange, u satisface necesariamente

{displaystyle nabla mathbf {u} ^{textsf {T}}mathbf {M} mathbf {u} -lambda cdot nabla mathbf {u} ^{textsf {T}}mathbf {u} =0}

para algún número real $λ$ . El símbolo nabla, $\nabla$ , es el operador del (diferenciación con respecto a x). Usando la simetría de $M$ obtenemos

{displaystyle nabla mathbf {x} ^{textsf {T}}mathbf {M} mathbf {x} -lambda cdot nabla mathbf {x} ^{textsf {T}}mathbf {x} =2(mathbf {M} -lambda mathbf {I})mathbf {x}.}

Por lo tanto $Mu = λ u$ , entonces u es un vector propio de longitud unitaria de $M$ . Para cada vector propio de longitud unitaria v de $M$ su valor propio es f(v ), por lo que $λ$ es el mayor valor propio de $M . El mismo cálculo realizado en el complemento ortogonal de u da el siguiente valor propio más grande y así sucesivamente. El complejo caso hermitiano es similar; hay f (x) = x * M x es una función de valor real de 2 n variables reales.$

Los valores singulares son similares en el sentido de que se pueden describir algebraicamente oa partir de principios variacionales. Aunque, a diferencia del caso de valores propios, la hermiticidad o simetría de $M$ ya no es necesaria.

Esta sección brinda estos dos argumentos para la existencia de la descomposición en valores singulares.

Basado en el teorema espectral

Vamos $mathbf {M}$ ser un $m \times n$ matriz compleja. Desde ${displaystyle mathbf {M} ^{*}mathbf {M} }$ es semi-definido positivo y Hermitian, por el teorema espectral, existe un $n \times n$ matriz unitaria $mathbf {V}$ tales que

{displaystyle mathbf {V} ^{*}mathbf {M} ^{*}mathbf {M} mathbf {V} ={bar {mathbf {D} }}={begin{bmatrix}mathbf {D} &0\0&0end{bmatrix}},}

Donde $mathbf{D}$ es diagonal y positivo definido, de dimensión ${displaystyle ell times ell }$ , con $ell$ el número de eigenvalues no cero de ${displaystyle mathbf {M} ^{*}mathbf {M} }$ (que se puede mostrar para verificar ${displaystyle ell leq min(n,m)}$ ). Note que $mathbf {V}$ está aquí por definición una matriz cuya $i$ - la columna es $i$ - el eigenvector de ${displaystyle mathbf {M} ^{*}mathbf {M} }$ , correspondiente al eigenvalue ${displaystyle {bar {mathbf {D} }}_{ii}}$ . Moreover, the $j$ -a columna de $mathbf {V}$ , para $ell }" xmlns="http://www.w3.org/1998/Math/MathML">j■l l {displaystyle j]ell }" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0561f8fcda12fc3725caaa6cd797040d73578c53" style="vertical-align: -0.671ex; margin-left: -0.027ex; width:5.053ex; height:2.509ex;"/>$ , es un eigenvector de ${displaystyle mathbf {M} ^{*}mathbf {M} }$ con eigenvalue ${displaystyle {bar {mathbf {D} }}_{jj}=0}$ . Esto se puede expresar por escrito $mathbf {V}$ como ${displaystyle mathbf {V} ={begin{bmatrix}mathbf {V} _{1}&mathbf {V} _{2}end{bmatrix}}}$ , donde las columnas de ${displaystyle mathbf {V} _{1}}$ y ${displaystyle mathbf {V} _{2}}$ por lo tanto contienen los eigenvectores de ${displaystyle mathbf {M} ^{*}mathbf {M} }$ correspondiente a valores no cero y cero eigenvalues, respectivamente. Usando esta reescritura $mathbf {V}$ , la ecuación se convierte en:

{displaystyle {begin{bmatrix}mathbf {V} _{1}^{*}\mathbf {V} _{2}^{*}end{bmatrix}}mathbf {M} ^{*}mathbf {M} {begin{bmatrix}mathbf {V} _{1}&mathbf {V} _{2}end{bmatrix}}={begin{bmatrix}mathbf {V} _{1}^{*}mathbf {M} ^{*}mathbf {M} mathbf {V} _{1}&mathbf {V} _{1}^{*}mathbf {M} ^{*}mathbf {M} mathbf {V} _{2}\mathbf {V} _{2}^{*}mathbf {M} ^{*}mathbf {M} mathbf {V} _{1}&mathbf {V} _{2}^{*}mathbf {M} ^{*}mathbf {M} mathbf {V} _{2}end{bmatrix}}={begin{bmatrix}mathbf {D} &0\0&0end{bmatrix}}.}

Esto implica que

{displaystyle mathbf {V} _{1}^{*}mathbf {M} ^{*}mathbf {M} mathbf {V} _{1}=mathbf {D}quad mathbf {V} _{2}^{*}mathbf {M} ^{*}mathbf {M} mathbf {V} _{2}=mathbf {0}.}

Además, la segunda ecuación implica ${displaystyle mathbf {M} mathbf {V} _{2}=mathbf {0} }$ . Finalmente, el carácter unitario $mathbf {V}$ traduce, en términos de ${displaystyle mathbf {V} _{1}}$ y ${displaystyle mathbf {V} _{2}}$ , en las siguientes condiciones:

{displaystyle {begin{aligned}mathbf {V} _{1}^{*}mathbf {V} _{1}&=mathbf {I} _{1},\mathbf {V} _{2}^{*}mathbf {V} _{2}&=mathbf {I} _{2},\mathbf {V} _{1}mathbf {V} _{1}^{*}+mathbf {V} _{2}mathbf {V} _{2}^{*}&=mathbf {I} _{12},end{aligned}}}

donde los subíndices de las matrices de identidad se utilizan para señalar que son de diferentes dimensiones.

Vamos a definir ahora

{displaystyle mathbf {U} _{1}=mathbf {M} mathbf {V} _{1}mathbf {D} ^{-{frac {1}{2}}}.}

Entonces,

{displaystyle mathbf {U} _{1}mathbf {D} ^{frac {1}{2}}mathbf {V} _{1}^{*}=mathbf {M} mathbf {V} _{1}mathbf {D} ^{-{frac {1}{2}}}mathbf {D} ^{frac {1}{2}}mathbf {V} _{1}^{*}=mathbf {M} (mathbf {I} -mathbf {V} _{2}mathbf {V} _{2}^{*})=mathbf {M} -(mathbf {M} mathbf {V} _{2})mathbf {V} _{2}^{*}=mathbf {M}}

desde entonces ${displaystyle mathbf {M} mathbf {V} _{2}=mathbf {0}.}$ Esto también puede considerarse como consecuencia inmediata del hecho de que ${displaystyle mathbf {M} mathbf {V} _{1}mathbf {V} _{1}^{*}=mathbf {M} }$ . Esto equivale a la observación de que si ${displaystyle {{boldsymbol {v}}_{i}}_{i=1}^{ell }}$ es el conjunto de eigenvectores de ${displaystyle mathbf {M} ^{*}mathbf {M} }$ correspondiente a los eigenvalues no-vanishing ${displaystyle {lambda _{i}}_{i=1}^{ell }}$ , entonces ${displaystyle {mathbf {M} {boldsymbol {v}}_{i}}_{i=1}^{ell }}$ es un conjunto de vectores ortogonales, y ${displaystyle {lambda _{i}^{-1/2}mathbf {M} {boldsymbol {v}}_{i}}_{i=1}^{ell }}$ es un conjunto (generalmente no completo) ortonormal vectores. Esto coincide con el formalismo de matriz utilizado anteriormente denotando con ${displaystyle mathbf {V} _{1}}$ la matriz cuyas columnas son ${displaystyle {{boldsymbol {v}}_{i}}_{i=1}^{ell }}$ , con ${displaystyle mathbf {V} _{2}}$ la matriz cuyas columnas son los eigenvectores de ${displaystyle mathbf {M} ^{*}mathbf {M} }$ con el eigenvalue desaparecido, y ${displaystyle mathbf {U} _{1}}$ la matriz cuyas columnas son los vectores ${displaystyle {lambda _{i}^{-1/2}mathbf {M} {boldsymbol {v}}_{i}}_{i=1}^{ell }}$ .

Vemos que este es casi el resultado deseado, excepto que ${displaystyle mathbf {U} _{1}}$ y ${displaystyle mathbf {V} _{1}}$ son en general no unitarios, ya que podrían no ser cuadrados. Sin embargo, sabemos que el número de filas de ${displaystyle mathbf {U} _{1}}$ no es menor que el número de columnas, ya que las dimensiones de $mathbf{D}$ no es mayor que $m$ y $n$ . También, desde

{displaystyle mathbf {U} _{1}^{*}mathbf {U} _{1}=mathbf {D} ^{-{frac {1}{2}}}mathbf {V} _{1}^{*}mathbf {M} ^{*}mathbf {M} mathbf {V} _{1}mathbf {D} ^{-{frac {1}{2}}}=mathbf {D} ^{-{frac {1}{2}}}mathbf {D} mathbf {D} ^{-{frac {1}{2}}}=mathbf {I_{1}}}

las columnas en ${displaystyle mathbf {U} _{1}}$ son ortonormales y pueden extenderse a una base ortonormal. Esto significa que podemos elegir ${displaystyle mathbf {U} _{2}}$ tales que $mathbf {U} ={begin{bmatrix}mathbf {U} _{1}&mathbf {U} _{2}end{bmatrix}}$ es unitario.

Para $V 1$ ya tenemos $V 2$ para hacerlo unitario. Ahora, define

{displaystyle {boldsymbol {Sigma }}={begin{bmatrix}{begin{bmatrix}mathbf {D} ^{frac {1}{2}}&0\0&0end{bmatrix}}\0end{bmatrix}},}

donde hay cero filas adicionales o eliminado para hacer el número de cero filas igual al número de columnas de $U 2$ , y por consiguiente las dimensiones generales $boldsymbol{Sigma}$ iguales $mtimes n$ . Entonces...

{displaystyle {begin{bmatrix}mathbf {U} _{1}&mathbf {U} _{2}end{bmatrix}}{begin{bmatrix}{begin{bmatrix}mathbf {} D^{frac {1}{2}}&0\0&0end{bmatrix}}\0end{bmatrix}}{begin{bmatrix}mathbf {V} _{1}&mathbf {V} _{2}end{bmatrix}}^{*}={begin{bmatrix}mathbf {U} _{1}&mathbf {U} _{2}end{bmatrix}}{begin{bmatrix}mathbf {D} ^{frac {1}{2}}mathbf {V} _{1}^{*}\0end{bmatrix}}=mathbf {U} _{1}mathbf {D} ^{frac {1}{2}}mathbf {V} _{1}^{*}=mathbf {M}}

cuál es el resultado deseado:

{displaystyle mathbf {M} =mathbf {U} {boldsymbol {Sigma }}mathbf {V} ^{*}.}

Observe que el argumento podría comenzar con la diagonalización de $MM ⁎$ en lugar de $M ⁎ M$ (Esto muestra directamente que $MM ⁎$ y $M ⁎ M$ tienen el mismo no -valores propios cero).

Basado en caracterización variacional

Los valores singulares también se pueden caracterizar como los máximos de $u T Mv$ , considerado como una función de $u$ y $v$ , sobre subespacios particulares. Los vectores singulares son los valores de $u$ y $v$ donde estos se alcanzan los máximos.

Vamos $M$ denote an $m \times n$ matriz con entradas reales. Vamos $S k -1$ ser la unidad $(k-1)$ - Esfera en ${displaystyle mathbb {R} ^{k}}$ , y definir ${displaystyle sigma (mathbf {u}mathbf {v})=mathbf {u} ^{textsf {T}}mathbf {M} mathbf {v} mathbf {u} in S^{m-1},mathbf {v} in S^{n-1}.}$

Considere la función $σ$ restringida a $S <sup m -1 \times S n -1$ . Dado que tanto $S m -1$ como $S n -1$ son conjuntos compactos, su producto también es compacto. Además, dado que $σ$ es continuo, alcanza un valor máximo para al menos un par de vectores $u \in S m -1$ y $v \in S n -1$ . Este valor mayor se denota $σ 1$ y los vectores correspondientes se denotan $u 1$ y $v 1$ . Dado que $σ 1$ es el mayor valor de $σ (u, v)$ debe ser no negativo. Si fuera negativo, cambiando el signo de $u 1$ o $v 1$ lo haría positivo y por lo tanto más grande.

Declaración. $u 1, v 1$ son vectores singulares izquierdo y derecho de $M$ con el valor singular correspondiente σ₁.

Prueba. Similar al caso de los valores propios, por suposición, los dos vectores satisfacen la ecuación del multiplicador de Lagrange:

{displaystyle nabla sigma =nabla mathbf {u} ^{textsf {T}}mathbf {M} mathbf {v} -lambda _{1}cdot nabla mathbf {u} ^{textsf {T}}mathbf {u} -lambda _{2}cdot nabla mathbf {v} ^{textsf {T}}mathbf {v} }

Después de un poco de álgebra, esto se convierte en

{displaystyle {begin{aligned}mathbf {M} mathbf {v} _{1}&=2lambda _{1}mathbf {u} _{1}+0\mathbf {M} ^{textsf {T}}mathbf {u} _{1}&=0+2lambda _{2}mathbf {v} _{1}end{aligned}}}

Multiplicando la primera ecuación de izquierda por ${displaystyle mathbf {u} _{1}^{textsf {T}}}$ y la segunda ecuación de izquierda por ${displaystyle mathbf {v} _{1}^{textsf {T}}}$ y tomar $Silencio u TENIDO ANTERIOR: Silencio v ANTERITORIO$ en cuenta

sigma _{1}=2lambda _{1}=2lambda _{2}.

Reemplazando esto en el par de ecuaciones de arriba, tenemos

{displaystyle {begin{aligned}mathbf {M} mathbf {v} _{1}&=sigma _{1}mathbf {u} _{1}\mathbf {M} ^{textsf {T}}mathbf {u} _{1}&=sigma _{1}mathbf {v} _{1}end{aligned}}}

Esto prueba la afirmación.

Se pueden encontrar más vectores singulares y valores singulares maximizando $σ (u, v)$ sobre $u, v$ normalizados que son ortogonales a $u 1$ y $v 1$ , respectivamente.

El paso de real a complejo es similar al caso del valor propio.

Calcular la SVD

(feminine)

La descomposición en valores singulares se puede calcular usando las siguientes observaciones:

Los vectores izquierdistas de $M$ son un conjunto de eigenvectores ortonormales de $MM ⁎$ .
Los vectores de línea derecha de $M$ son un conjunto de eigenvectores ortonormales de $M ⁎ M$ .
Los valores no cero singulares de $M$ (encontrado en las entradas diagonales de $mathbf{Sigma}$ ) son las raíces cuadradas de los eigenvalues no cero de ambos $M ⁎ M$ y $MM ⁎$ .

Enfoque numérico

La SVD de una matriz $M$ normalmente se calcula mediante un procedimiento de dos pasos. En el primer paso, la matriz se reduce a una matriz bidiagonal. Esto toma O(mn²) operaciones de punto flotante (flop), suponiendo que m ≥ n. El segundo paso es calcular la SVD de la matriz bidiagonal. Este paso solo se puede realizar con un método iterativo (como con los algoritmos de valores propios). Sin embargo, en la práctica es suficiente calcular el SVD hasta cierta precisión, como la máquina épsilon. Si esta precisión se considera constante, entonces el segundo paso toma O(n) iteraciones, cada una de las cuales cuesta O(n) fracasos. Por lo tanto, el primer paso es más costoso y el costo total es O(mn²) fracasos (Trefethen & Bau III 1997, Lecture 31).

El primer paso se puede realizar utilizando los reflejos del amo de casa por un costo de 4mn² − 4n³/3 flops, suponiendo que solo se necesitan los valores singulares y no los vectores singulares. Si m es mucho mayor que n entonces es ventajoso reducir primero la matriz $M$ a una matriz triangular con la descomposición QR y luego use reflexiones de Houseer para reducir aún más la matriz a la forma bidiagonal; el costo combinado es 2mn² + 2n³ flops (Trethethen & Bau III 1997, Lecture 31).

El segundo paso se puede realizar mediante una variante del algoritmo QR para el cálculo de valores propios, que fue descrito por primera vez por Golub & Kanan (1965). La subrutina DBDSQR de LAPACK implementa este método iterativo, con algunas modificaciones para cubrir el caso donde los valores singulares son muy pequeños (Demmel & Kahan 1990). Junto con un primer paso que utiliza reflexiones de Householder y, si corresponde, descomposición QR, esto forma la rutina DGESVD para el cálculo de la descomposición de valor singular.

El mismo algoritmo se implementa en la Biblioteca científica GNU (GSL). El GSL también ofrece un método alternativo que utiliza una ortogonalización de Jacobi unilateral en el paso 2 (GSL Team 2007). Este método calcula la SVD de la matriz bidiagonal resolviendo una secuencia de problemas SVD de 2 × 2, similar a cómo el algoritmo de valores propios de Jacobi resuelve una secuencia de métodos de valores propios de 2 × 2 (Golub & Van Loan 1996, §8.6.3). Otro método más para el paso 2 utiliza la idea de algoritmos de valores propios de divide y vencerás (Trefethen & Bau III 1997, Lecture 31).

Hay una forma alternativa que no usa explícitamente la descomposición de valores propios. Por lo general, el problema de valor singular de una matriz $M$ se convierte en un problema de valor propio simétrico equivalente como $M M ⁎$ , $M ⁎ M$ , o

{displaystyle {begin{bmatrix}mathbf {O} &mathbf {M} \mathbf {M} ^{*}&mathbf {O} end{bmatrix}}.}

Los enfoques que utilizan descomposiciones de valores propios se basan en el algoritmo QR, que está bien desarrollado para ser estable y rápido. Tenga en cuenta que los valores singulares son reales y que los vectores singulares derecho e izquierdo no son necesarios para formar transformaciones de similitud. Se puede alternar iterativamente entre la descomposición QR y la descomposición LQ para encontrar las matrices hermitianas diagonales reales. La descomposición QR da $M \Rightarrow Q R$ y la descomposición LQ de $R$ da $R \Rightarrow L P ⁎$ . Por lo tanto, en cada iteración, tenemos $M \Rightarrow Q L P ⁎$ , actualizar $M \Leftarrow L$ y repite las ortogonalizaciones. Eventualmente, esta iteración entre la descomposición QR y la descomposición LQ produce matrices singulares unitarias izquierda y derecha. Este enfoque no se puede acelerar fácilmente, como lo hace el algoritmo QR con cambios espectrales o deflación. Esto se debe a que el método de cambio no se define fácilmente sin usar transformaciones de similitud. Sin embargo, este enfoque iterativo es muy simple de implementar, por lo que es una buena opción cuando la velocidad no importa. Este método también proporciona información sobre cómo las transformaciones puramente ortogonales/unitarias pueden obtener la SVD.

Resultado analítico de 2 × 2 SVD

Los valores singulares de una matriz 2 × 2 se pueden encontrar analíticamente. Que la matriz sea $mathbf {M} =z_{0}mathbf {I} +z_{1}sigma _{1}+z_{2}sigma _{2}+z_{3}sigma _{3}$

Donde $z_{i}in mathbb {C}$ son números complejos que parametizan la matriz, $I$ es la matriz de identidad, y $sigma _{i}$ denota las matrices Pauli. Entonces sus dos valores singulares son dados por

{displaystyle {begin{aligned}sigma _{pm }&={sqrt {|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}pm {sqrt {(|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2})^{2}-|z_{0}^{2}-z_{1}^{2}-z_{2}^{2}-z_{3}^{2}|^{2}}}}}\&={sqrt {|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}pm 2{sqrt {(operatorname {Re} z_{0}z_{1}^{*})^{2}+(operatorname {Re} z_{0}z_{2}^{*})^{2}+(operatorname {Re} z_{0}z_{3}^{*})^{2}+(operatorname {Im} z_{1}z_{2}^{*})^{2}+(operatorname {Im} z_{2}z_{3}^{*})^{2}+(operatorname {Im} z_{3}z_{1}^{*})^{2}}}}}end{aligned}}}

SVD reducidos

Visualización de variantes SVD reducidas. De arriba a abajo: 1: Full SVD, 2: Thin SVD (remove columns of U not corresponding to rows of V*), 3: Compact SVD (remove desvanecing singular values and corresponding columns/rows in U and V*), 4: SVD truncado (Mantenga sólo los valores t singulares más grandes y las columnas/rows correspondientes en U y V*)

En las aplicaciones, es bastante inusual que se requiera el SVD completo, incluida una descomposición unitaria completa del espacio nulo de la matriz. En cambio, a menudo es suficiente (así como más rápido y más económico para el almacenamiento) calcular una versión reducida del SVD. Se puede distinguir lo siguiente para una matriz m×n M de rango r:

SVD fino

El SVD delgado, o de tamaño económico, de una matriz M viene dado por

{displaystyle mathbf {M} =mathbf {U} _{k}{boldsymbol {Sigma }}_{k}mathbf {V} _{k}^{*},}

dónde

{displaystyle k=operatorname {min} (m,n)}

las matrices U_k y V_k contienen solo las primeras columnas k de U y V, y Σ_k contiene solo los primeros k valores singulares de Σ. La matriz U_k es entonces m×k, Σ_k es k×k diagonal, y V_k* es k×n.

El SVD delgado usa significativamente menos espacio y tiempo de cálculo si k ≪ max(m, n). La primera etapa de su cálculo suele ser una descomposición QR de M, que puede hacer que el cálculo sea significativamente más rápido en este caso.

SVD compacta

(feminine)

mathbf {M} =mathbf {U} _{r}{boldsymbol {Sigma }}_{r}mathbf {V} _{r}^{*}

Solo los vectores columna r de U y los vectores fila r de V* correspondientes a los vectores no Se calculan los valores cero singulares Σ_r. Los vectores restantes de U y V* no se calculan. Esto es más rápido y económico que el SVD delgado si r ≪ min(m, n). La matriz U_r es entonces m×r, Σ_r es r×r diagonal, y V_r* es r×n.

SVD truncada

(feminine)

En muchas aplicaciones el número r de los valores no cero singulares es grande haciendo incluso el compacto SVD poco práctico para calcular. En tales casos, los valores singulares más pequeños pueden necesitar ser truncados sólo para calcular t≪r valores no singulares. El SVD truncado ya no es una descomposición exacta de la matriz original M, pero más bien proporciona la aproximación óptima de la matriz de bajo rango ${tilde {mathbf {M} }}$ por cualquier matriz de un rango fijot

{tilde {mathbf {M} }}=mathbf {U} _{t}{boldsymbol {Sigma }}_{t}mathbf {V} _{t}^{*}

donde la matriz U_t es m×t, Σ<sub t es t×t diagonal, y V_t* es t×n. Solo los vectores columna t de U y los vectores fila t de V* correspondientes a la t se calculan los valores singulares más grandes Σ_t. Esto puede ser mucho más rápido y económico que el SVD compacto si t≪r, pero requiere un conjunto de herramientas completamente diferente de solucionadores numéricos.

En aplicaciones que requieren una aproximación a la inversa de Moore-Penrose de la matriz M, son de interés los valores singulares más pequeños de M, que son más difíciles de calcular en comparación con los más grandes.

La SVD truncada se emplea en la indexación semántica latente.

Normas

Normas de Ky Fan

La suma de los k valores singulares más grandes de M es una norma matricial, la norma Ky Fan k de M .

La primera de las normas Ky Fan, la norma Ky Fan 1, es la misma que la norma del operador de M como operador lineal con respecto a las normas euclidianas de K^m y Kⁿ. En otras palabras, la norma Ky Fan 1 es la norma del operador inducida por el producto interno euclidiano ℓ² estándar. Por esta razón, también se le llama operador 2-norma. Uno puede verificar fácilmente la relación entre la norma Ky Fan 1 y los valores singulares. Es cierto en general, para un operador acotado M en espacios de Hilbert (posiblemente de dimensión infinita)

|mathbf {M} |=|mathbf {M} ^{*}mathbf {M} |^{frac {1}{2}}

Pero, en el caso de la matriz, (M* M)^1/2 es una matriz normal, entonces ||M* M ||^1/2 es el mayor valor propio de (M* M)^1/2, es decir, el mayor valor singular de M .

La última de las normas de Ky Fan, la suma de todos los valores singulares, es la norma traza (también conocida como la 'norma nuclear'), definida por ||M || = Tr[(M* M)^1/2] (los valores propios de M* M son los cuadrados de los valores singulares).

Norma de Hilbert-Schmidt

Los valores singulares están relacionados con otra norma sobre el espacio de operadores. Considere el producto interno de Hilbert-Schmidt en las matrices $n \times n$ , definidas por

{displaystyle langle mathbf {M}mathbf {N} rangle =operatorname {tr} left(mathbf {N} ^{*}mathbf {M} right).}

Entonces la norma inducida es

{displaystyle |mathbf {M} |={sqrt {langle mathbf {M}mathbf {M} rangle }}={sqrt {operatorname {tr} left(mathbf {M} ^{*}mathbf {M} right)}}.}

Dado que la traza es invariante bajo equivalencia unitaria, esto muestra

|mathbf {M} |={sqrt {sum _{i}sigma _{i}^{2}}}

donde $σ i$ son los valores singulares de $M$ . Esto se denomina norma Frobenius, norma Schatten 2 o norma Hilbert-Schmidt de $M$ . El cálculo directo muestra que la norma de Frobenius de $M = (m ij)$ coincide con:

{sqrt {sum _{ij}|m_{ij}|^{2}}}.

Además, la norma de Frobenius y la norma de trazas (la norma nuclear) son casos especiales de la norma de Schatten.

Variaciones y generalizaciones

Representación de modo-k

${displaystyle M=USV^{textsf {T}}}$ puede ser representado mediante la multiplicación de modo-k de matriz $S$ aplicación ${displaystyle times _{1}U}$ entonces ${displaystyle times _{2}V}$ sobre el resultado; ${displaystyle M=Stimes _{1}Utimes _{2}V}$ .

Tensor SVD

Existen dos tipos de descomposiciones tensoriales, que generalizan la SVD a arreglos multidireccionales. Uno de ellos descompone un tensor en una suma de tensores de rango 1, lo que se denomina descomposición de rango de tensores. El segundo tipo de descomposición calcula los subespacios ortonormales asociados con los diferentes factores que aparecen en el producto tensorial de espacios vectoriales en los que vive el tensor. Esta descomposición se denomina en la literatura SVD de orden superior (HOSVD) o Tucker3/TuckerM. Además, el análisis de componentes principales multilineal en el aprendizaje subespacial multilineal implica las mismas operaciones matemáticas que la descomposición de Tucker, y se utiliza en un contexto diferente de reducción de dimensionalidad.

SVD de escala invariable

Los valores singulares de una matriz A están definidos de forma única y son invariantes con respecto a las transformaciones unitarias izquierda y/o derecha de A. En otras palabras, los valores singulares de UAV, para U y V unitarios, son iguales a los valores singulares de A. Esta es una propiedad importante para aplicaciones en las que es necesario preservar las distancias euclidianas y la invariancia con respecto a las rotaciones.

La SVD invariante de escala, o SI-SVD, es análoga a la SVD convencional excepto que sus valores singulares determinados de forma única son invariantes con respecto a las transformaciones diagonales de A. En otras palabras, los valores singulares de DAE, para matrices diagonales invertibles D y E, son iguales a los valores singulares de A . Esta es una propiedad importante para las aplicaciones en las que se necesita invariancia en la elección de unidades en las variables (por ejemplo, unidades métricas frente a unidades imperiales).

SVD de funciones de orden superior (HOSVD)

La transformación del modelo de producto tensorial (TP) reconstruye numéricamente el HOSVD de las funciones. Para más detalles por favor visite:

Transformación del modelo de producto de tensor
Forma canónica basada en HOSVD de funciones TP y modelos qLPV
Transformación modelo TP en la teoría del control

Operadores acotados en espacios de Hilbert

La factorización $M = UΣV ⁎$ se puede extender a un operador acotado M en un espacio separable de Hilbert H. Es decir, para cualquier operador acotado M, existe una isometría parcial U, una V unitaria, un espacio de medida (X, μ), y una f medible no negativa tal que

mathbf {M} =mathbf {U} T_{f}mathbf {V} ^{*}

Donde $T_{f}$ es la multiplicación por f encendido L²()X, μ).

Esto se puede demostrar imitando el argumento algebraico lineal para el caso matricial anterior. VT_fV* es la única raíz cuadrada positiva de M*M, como lo da el cálculo funcional de Borel para operadores autoadjuntos. La razón por la cual U no necesita ser unitario es porque, a diferencia del caso de dimensión finita, dada una isometría U₁ con kernel no trivial, un adecuado U₂ no se puede encontrar tal que

{begin{bmatrix}U_{1}\U_{2}end{bmatrix}}

es un operador unitario.

En cuanto a las matrices, la factorización de valores singulares es equivalente a la descomposición polar para operadores: simplemente podemos escribir

mathbf {M} =mathbf {U} mathbf {V} ^{*}cdot mathbf {V} T_{f}mathbf {V} ^{*}

y observe que U V* sigue siendo una isometría parcial mientras que VT_fV* es positivo.

Valores singulares y operadores compactos

La noción de valores singulares y vectores singulares izquierdo/derecho se puede extender al operador compacto en el espacio de Hilbert, ya que tienen un espectro discreto. Si $T$ es compacto, cada $λ$ en su espectro es un valor propio. Además, un operador autoadjunto compacto puede ser diagonalizado por sus vectores propios. Si $M$ es compacto, también lo es $M ⁎ M$ . Aplicando el resultado de la diagonalización, la imagen unitaria de su raíz cuadrada positiva $T f$ tiene un conjunto de ortonormales vectores propios ${e i}$ correspondientes a valores propios estrictamente positivos ${σ i}$ . Para cualquier $ψ \in H$ ,

{displaystyle mathbf {M} psi =mathbf {U} T_{f}mathbf {V} ^{*}psi =sum _{i}leftlangle mathbf {U} T_{f}mathbf {V} ^{*}psimathbf {U} e_{i}rightrangle mathbf {U} e_{i}=sum _{i}sigma _{i}leftlangle psimathbf {V} e_{i}rightrangle mathbf {U} e_{i},}

donde la serie converge en la topología normal en $H$ . Observe cómo esto se parece a la expresión del caso de dimensión finita. $σ i$ son los valores singulares de $M$ . ${U e i}$ (resp. ${V e i}$ ) pueden considerarse los vectores del singular a la izquierda (resp. al singular a la derecha) de $M$ .

Los operadores compactos en un espacio de Hilbert son el cierre de operadores de rango finito en la topología de operadores uniformes. La expresión de la serie anterior da una representación explícita de este tipo. Una consecuencia inmediata de esto es:

Teorema.

M

es compacto si y sólo si

M ⁎ M

es compacto.

Historia

La descomposición en valores singulares fue desarrollada originalmente por geómetras diferenciales, que deseaban determinar si una forma bilineal real podía igualarse a otra mediante transformaciones ortogonales independientes de los dos espacios sobre los que actúa. Eugenio Beltrami y Camille Jordan descubrieron de forma independiente, en 1873 y 1874 respectivamente, que los valores singulares de las formas bilineales, representados como una matriz, forman un conjunto completo de invariantes para formas bilineales bajo sustituciones ortogonales. James Joseph Sylvester también llegó a la descomposición en valores singulares para matrices cuadradas reales en 1889, aparentemente independientemente tanto de Beltrami como de Jordan. Sylvester llamó a los valores singulares los multiplicadores canónicos de la matriz A. El cuarto matemático en descubrir la descomposición en valores singulares de forma independiente es Autonne en 1915, quien llegó a ella a través de la descomposición polar. La primera prueba de la descomposición en valores singulares para matrices rectangulares y complejas parece ser de Carl Eckart y Gale J. Young en 1936; lo vieron como una generalización de la transformación del eje principal para matrices hermitianas.

En 1907, Erhard Schmidt definió un analógico de valores singulares para los operadores integrales (que son compactos, bajo algunas suposiciones técnicas débiles); parece que no tenía conocimiento del trabajo paralelo sobre valores singulares de matrices finitas. Esta teoría fue desarrollada por Émile Picard en 1910, quien es el primero en llamar a los números $sigma _{k}$ Valores singulares (o en francés, valeurs singulières).

Los métodos prácticos para calcular el SVD se remontan a Kogbetliantz en 1954-1955 y Hestenes en 1958, y se asemejan mucho al algoritmo de valor propio de Jacobi, que usa rotaciones planas o rotaciones de Givens. Sin embargo, estos fueron reemplazados por el método de Gene Golub y William Kahan publicado en 1965, que utiliza transformaciones o reflejos de Householder. En 1970, Golub y Christian Reinsch publicaron una variante del algoritmo Golub/Kahan que sigue siendo el más utilizado en la actualidad.