UPGMA
UPGMA (método de grupos de pares no ponderados con media aritmética) es un método de agrupación jerárquica aglomerativo (de abajo hacia arriba) simple. También tiene una variante ponderada, WPGMA, y generalmente se atribuyen a Sokal y Michener.
Tenga en cuenta que el término no ponderado indica que todas las distancias contribuyen igualmente a cada promedio que se calcula y no se refiere a las matemáticas mediante las cuales se logra. Por lo tanto, el promedio simple en WPGMA produce un resultado ponderado y el promedio proporcional en UPGMA produce un resultado no ponderado (ver el ejemplo práctico).
Algoritmo
El algoritmo de UPGMA construye un árbol arraigado (dendrograma) que refleja la estructura presente en una matriz de similitud pareado (o una matriz de disimilaridad). A cada paso, los dos grupos más cercanos se combinan en un grupo de alto nivel. La distancia entre dos grupos A{displaystyle {fnMithcal}} y B{displaystyle {máthcal {B}}, cada uno de tamaño (i.e., cardenalidad) SilencioASilencio{displaystyle {fnMithcal {fnh}¿Por qué? y SilencioBSilencio{displaystyle {fnMitcal {fnh}¿Por qué?, se toma para ser el promedio de todas las distancias d()x,Sí.){displaystyle d(x,y)} entre pares de objetos x{displaystyle x} dentro A{displaystyle {fnMithcal}} y Sí.{displaystyle y} dentro B{displaystyle {máthcal {B}}, es decir, la distancia media entre elementos de cada grupo:
- 1SilencioASilencio⋅ ⋅ SilencioBSilencio.. x▪ ▪ A.. Sí.▪ ▪ Bd()x,Sí.){displaystyle {1 over {fncipal {fnh} {cdot}cdot âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTM
En otras palabras, en cada paso de agrupación, la distancia actualizada entre los grupos unidos A∪ ∪ B{displaystyle {fnMithcal {fnMicrosoft} {fnMicrosoft Sans Serif}} {fnK} y un nuevo grupo X{displaystyle X} se da por el promedio proporcional de la dA,X{fnMicrosoft Sans Serif} y dB,X{fnMicrosoft Sans Serif} distancias:
d()A∪ ∪ B),X=SilencioASilencio⋅ ⋅ dA,X+SilencioBSilencio⋅ ⋅ dB,XSilencioASilencio+SilencioBSilencio{displaystyle d_{fnMitcal {fn}cup {fnMitcal {fn}}={frac} {fnMitcal {fnMicrosoft} ♪♪{mathcal {A}},X}+Sobrevivir {mathcal {B} ♪♪{mathcal {B},X} {fnh} {fnh} {fnh}} {fnh}}} {fn}}} {fn}}} {fn}}}}}}} {fn}}}}}}}}} {fn}}}}} {fnH}}}}}}}}}}}}} {\\\\}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
El algoritmo UPGMA produce dendrogramas enraizados y requiere una suposición de tasa constante, es decir, asume un árbol ultramétrico en el que las distancias desde la raíz hasta cada punta de rama son iguales. Cuando las puntas son datos moleculares (es decir,, ADN, ARN y proteínas) muestreados al mismo tiempo, la suposición de ultrametricidad se vuelve equivalente a asumir un reloj molecular.
Ejemplo de trabajo
Este ejemplo de trabajo se basa en una matriz de distancia genética JC69 calculada de la secuencia de 5S ribosomal RNA alineada de cinco bacterias: Bacillus subtilis ()a{displaystyle a}), Bacillus stearothermophilus ()b{displaystyle b}), Lactobacillus viridescens ()c{displaystyle c}), Acholeplasma modicum ()d{displaystyle d}), y Micrococcus luteus ()e{displaystyle e}).
Primer paso
- Primera agrupación
Supongamos que tenemos cinco elementos ()a,b,c,d,e){displaystyle (a,b,c,d,e)} y la siguiente matriz D1{displaystyle D_{1} de distancias pares entre ellos:
Did you mean:
| a | b | c | d | e | |
|---|---|---|---|---|---|
| a | 0 | 17 | 21 | 31 | 23 |
| b | 17 | 0 | 30 | 34 | 21 |
| c | 21 | 30 | 0 | 28 | 39 |
| d | 31 | 34 | 28 | 0 | 43 |
| e | 23 | 21 | 39 | 43 | 0 |
En este ejemplo, D1()a,b)=17{displaystyle D_{1}(a,b)=17} es el valor más pequeño de D1{displaystyle D_{1}, así que nos unimos a elementos a{displaystyle a} y b{displaystyle b}.
- Primera estimación de longitud de rama
Vamos u{displaystyle u} denota el nodo al que a{displaystyle a} y b{displaystyle b} están conectados. Ajuste δ δ ()a,u)=δ δ ()b,u)=D1()a,b)/2{displaystyle delta (a,u)=delta (b,u)=D_{1}(a,b)/2} asegura que los elementos a{displaystyle a} y b{displaystyle b} son equidistas de u{displaystyle u}. Esto corresponde a la expectativa de la hipótesis de ultrametría. Las ramas que unen a{displaystyle a} y b{displaystyle b} a u{displaystyle u} entonces tienen longitudes δ δ ()a,u)=δ δ ()b,u)=17/2=8,5{displaystyle delta (a,u)=delta (b,u)=17/2=8.5} ()ver el dendrograma final)
- Actualización de matriz de primera distancia
Luego procederemos a actualizar la matriz de distancia inicial D1{displaystyle D_{1} en una nueva matriz de distancia D2{displaystyle D_{2} (ver abajo), reducido en tamaño por una fila y una columna debido a la agrupación de a{displaystyle a} con b{displaystyle b}. Valores Bold en D2{displaystyle D_{2} corresponde a las nuevas distancias, calculadas por distancias promedio entre cada elemento del primer grupo ()a,b){displaystyle (a,b)} y cada uno de los elementos restantes:
D2()()a,b),c)=()D1()a,c)× × 1+D1()b,c)× × 1)/()1+1)=()21+30)/2=25,5{displaystyle D_{2}(a,b),c)=(D_{1}(a,c)times 1+D_{1}(b,c)times 1)/(1+1)=(21+30)/2=25.5}
D2()()a,b),d)=()D1()a,d)+D1()b,d))/2=()31+34)/2=32,5{displaystyle D_{2}(a,b),d)=(D_{1}(a,d)+D_{1}(b,d)/2=(31+34)/2=32.5}
D2()()a,b),e)=()D1()a,e)+D1()b,e))/2=()23+21)/2=22{displaystyle D_{2}(a,b),e)=(D_{1}(a,e)+D_{1}(b,e)/2=(23+21)/2=22}
Valores Italicizados en D2{displaystyle D_{2} no se ven afectados por la actualización de matriz, ya que corresponden a distancias entre elementos no involucrados en el primer grupo.
Segundo paso
- Segunda agrupación
Reiteramos ahora los tres pasos anteriores, a partir de la nueva matriz de distancia D2{displaystyle D_{2}
| ab) | c | d | e | |
|---|---|---|---|---|
| ab) | 0 | 25,5 | 32,5 | 22 |
| c | 25,5 | 0 | 28 | 39 |
| d | 32,5 | 28 | 0 | 43 |
| e | 22 | 39 | 43 | 0 |
Aquí, D2()()a,b),e)=22{displaystyle D_{2}(a,b),e)=22} es el valor más pequeño de D2{displaystyle D_{2}, así que nos unimos al grupo ()a,b){displaystyle (a,b)} y elemento e{displaystyle e}.
- Estimación de la longitud de la segunda rama
Vamos v{displaystyle v} denota el nodo al que ()a,b){displaystyle (a,b)} y e{displaystyle e} están conectados. Debido a la limitación de ultrametría, las ramas se unen a{displaystyle a} o b{displaystyle b} a v{displaystyle v}, y e{displaystyle e} a v{displaystyle v} son iguales y tienen la siguiente longitud: δ δ ()a,v)=δ δ ()b,v)=δ δ ()e,v)=22/2=11{displaystyle delta (a,v)=delta (b,v)=delta (e,v)=22/2=11}
Deducimos la longitud de la rama desaparecida: δ δ ()u,v)=δ δ ()e,v)− − δ δ ()a,u)=δ δ ()e,v)− − δ δ ()b,u)=11− − 8,5=2.5{displaystyle delta (u,v)=delta (e,v)-delta (a,u)=delta (e,v)-delta (b,u)=11-8.5=2.5} ()ver el dendrograma final)
- Segunda actualización de la matriz de distancia
Luego procederemos a la actualización D2{displaystyle D_{2} en una nueva matriz de distancia D3{displaystyle D_{3} (ver abajo), reducido en tamaño por una fila y una columna debido a la agrupación de ()a,b){displaystyle (a,b)} con e{displaystyle e}. Valores Bold en D3{displaystyle D_{3} corresponde a las nuevas distancias, calculadas por promedio proporcional:
D3()()()a,b),e),c)=()D2()()a,b),c)× × 2+D2()e,c)× × 1)/()2+1)=()25,5× × 2+39× × 1)/3=30{displaystyle D_{3}((a,b),e),c)=(D_{2}(a,b),c)times 2+D_{2}(e,c)times 1)/(2+1)=(25.5times 2+39times 1)/3=30}
Gracias a este promedio proporcional, el cálculo de esta nueva distancia representa el tamaño más grande del ()a,b){displaystyle (a,b)} cluster (two elements) with respect to e{displaystyle e} (un elemento). Análogamente:
D3()()()a,b),e),d)=()D2()()a,b),d)× × 2+D2()e,d)× × 1)/()2+1)=()32,5× × 2+43× × 1)/3=36{displaystyle D_{3}((a,b),e),d)=(D_{2}(a,b),d)times 2+D_{2}(e,d)times 1)/(2+1)=(32.5times 2+43times 1)/3=36}
Por lo tanto, el promedio proporcional da igual peso a las distancias iniciales de la matriz D1{displaystyle D_{1}. Esta es la razón por la cual el método es sin peso, no con respecto al procedimiento matemático sino con respecto a las distancias iniciales.
Tercer paso
- Tercera agrupación
Reiteramos de nuevo los tres pasos anteriores, a partir de la matriz de distancia actualizada D3{displaystyle D_{3}.
| (a,b),e) | c | d | |
|---|---|---|---|
| (a,b),e) | 0 | 30 | 36 |
| c | 30 | 0 | 28 |
| d | 36 | 28 | 0 |
Aquí, D3()c,d)=28{displaystyle D_{3}(c,d)=28} es el valor más pequeño de D3{displaystyle D_{3}, así que nos unimos a elementos c{displaystyle c} y d{displaystyle d}.
- Estimación de la longitud de la tercera rama
Vamos w{displaystyle w} denota el nodo al que c{displaystyle c} y d{displaystyle d} están conectados. Las ramas que unen c{displaystyle c} y d{displaystyle d} a w{displaystyle w} entonces tienen longitudes δ δ ()c,w)=δ δ ()d,w)=28/2=14{displaystyle delta (c,w)=delta (d,w)=28/2=14} ()ver el dendrograma final)
- Actualización de la matriz de tercera distancia
Hay una sola entrada para actualizar, teniendo en cuenta que los dos elementos c{displaystyle c} y d{displaystyle d} cada uno tiene una contribución 1{displaystyle 1} en el computación promedio:
D4()()c,d),()()a,b),e))=()D3()c,()()a,b),e))× × 1+D3()d,()()a,b),e))× × 1)/()1+1)=()30× × 1+36× × 1)/2=33{displaystyle D_{4}(c,d),(a,b),e)=(D_{3}(c,(a,b),e))times 1+D_{3}(d,(a,b),e)times 1)/(1+1)=(30times 1+36times 1)/2=33}
Paso final
La final D4{displaystyle D_{4} matriz es:
| (a,b),e) | c, d) | |
|---|---|---|
| (a,b),e) | 0 | 33 |
| c, d) | 33 | 0 |
Así que nos unimos a grupos ()()a,b),e){displaystyle ((a,b),e)} y ()c,d){displaystyle (c,d)}.
Vamos r{displaystyle r} denota el nodo (root) al que ()()a,b),e){displaystyle ((a,b),e)} y ()c,d){displaystyle (c,d)} están conectados. Las ramas que unen ()()a,b),e){displaystyle ((a,b),e)} y ()c,d){displaystyle (c,d)} a r{displaystyle r} entonces tienen longitudes:
δ δ ()()()a,b),e),r)=δ δ ()()c,d),r)=33/2=16,5{displaystyle delta ((a,b),e),r)=delta ((c,d),r)=33/2=16.5}
Deducimos las dos longitudes de rama restantes:
δ δ ()v,r)=δ δ ()()()a,b),e),r)− − δ δ ()e,v)=16,5− − 11=5,5{displaystyle delta (v,r)=delta ((a,b),e),r)-delta (e,v)=16.5-11=5.5}
δ δ ()w,r)=δ δ ()()c,d),r)− − δ δ ()c,w)=16,5− − 14=2.5{displaystyle delta (w,r)=delta (c,d),r)-delta (c,w)=16.5-14=2.5}
El dendrograma de la UPGMA
Did you mean:
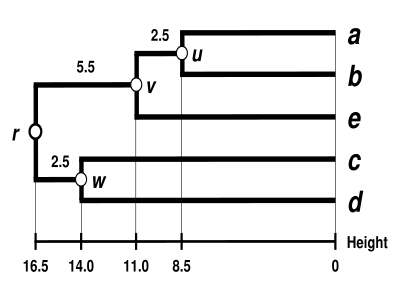
El dendrograma ya está completo. Es ultramétrico porque todos los consejos (a{displaystyle a} a e{displaystyle e}) son equidistantes de r{displaystyle r}:
δ δ ()a,r)=δ δ ()b,r)=δ δ ()e,r)=δ δ ()c,r)=δ δ ()d,r)=16,5{displaystyle delta (a,r)=delta (b,r)=delta (e,r)=delta (c,r)=delta (d,r)=16.5}
Por lo tanto, el dendrograma está arraigado por r{displaystyle r}, su nodo más profundo.
Comparación con otros enlaces
Los esquemas de vinculación alternativos incluyen agrupación de vinculación única, agrupación de vinculación completa y agrupación de vinculación promedio WPGMA. Implementar un vínculo diferente es simplemente una cuestión de usar una fórmula diferente para calcular las distancias entre grupos durante los pasos de actualización de la matriz de distancias del algoritmo anterior. La agrupación de enlaces completos evita un inconveniente del método alternativo de agrupación de enlaces únicos: el llamado fenómeno de encadenamiento, donde los grupos formados a través de agrupaciones de enlaces únicos pueden verse obligados a unirse debido a que los elementos individuales están cerca unos de otros, incluso aunque muchos de los elementos de cada grupo pueden estar muy distantes entre sí. El enlace completo tiende a encontrar grupos compactos de diámetros aproximadamente iguales.
Usos
- En la ecología, es uno de los métodos más populares para la clasificación de unidades de muestreo (como parcelas de vegetación) sobre la base de sus similitudes pares en variables descriptoras relevantes (como composición de especies). Por ejemplo, se ha utilizado para comprender la interacción trófica entre bacterias marinas y protistas.
- En bioinformática, UPGMA se utiliza para la creación de árboles fenéticos (fenografías). UPGMA fue diseñado inicialmente para su uso en estudios de electroforesis de proteínas, pero actualmente se utiliza más a menudo para producir árboles guía para algoritmos más sofisticados. Este algoritmo se utiliza por ejemplo en los procedimientos de alineación de secuencias, ya que propone un orden en el que se alinearán las secuencias. De hecho, el árbol guía pretende agrupar las secuencias más similares, independientemente de su tasa evolutiva o afinidades filogenéticas, y ese es exactamente el objetivo de la UPGMA
- En la filogenética, UPGMA asume una tasa constante de evolución (hipótesis del reloj molecular) y que todas las secuencias fueron muestreadas al mismo tiempo, y no es un método bien registrado para inferir relaciones a menos que esta suposición haya sido probada y justificada para el conjunto de datos que se utiliza. Observe que incluso bajo un reloj de restricción, las secuencias muestreadas en diferentes momentos no deben llevar a un árbol ultramétrico.
Complejidad del tiempo
Una implementación trivial del algoritmo para construir el árbol UPGMA tiene O()n3){displaystyle O(n^{3}} la complejidad del tiempo y el uso de un montón para cada grupo para mantener sus distancias de otro grupo reduce su tiempo a O()n2log n){displaystyle O(n^{2}log n)}. Fionn Murtagh presentó un O()n2){displaystyle O(n^{2}} algoritmo de tiempo y espacio.
Contenido relacionado
TAT-10
Breguet
Acceso directo























































