Trigonometría

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

La trigonometría (del griego antiguo τρίγωνον (trígōnon) 'triángulo' y μέτρον (métron) 'medida') es una rama de las matemáticas que estudia las relaciones entre las longitudes de los lados y los ángulos de los triángulos. El campo surgió en el mundo helenístico durante el siglo III a. C. a partir de las aplicaciones de la geometría a los estudios astronómicos. Los griegos se centraron en el cálculo de cuerdas, mientras que los matemáticos de la India crearon las tablas de valores más antiguas conocidas para proporciones trigonométricas (también llamadas funciones trigonométricas) como el seno.

A lo largo de la historia, la trigonometría se ha aplicado en áreas como la geodesia, la topografía, la mecánica celeste y la navegación.

La trigonometría es conocida por sus muchas identidades. Estas identidades trigonométricas se usan comúnmente para reescribir expresiones trigonométricas con el objetivo de simplificar una expresión, encontrar una forma más útil de una expresión o resolver una ecuación.

Historia

Los astrónomos sumerios estudiaron la medida de los ángulos, usando una división de círculos en 360 grados. Ellos, y más tarde los babilonios, estudiaron las proporciones de los lados de triángulos semejantes y descubrieron algunas propiedades de estas proporciones, pero no las convirtieron en un método sistemático para hallar los lados y los ángulos de los triángulos. Los antiguos nubios usaban un método similar.

En el siglo III a. C., matemáticos helenísticos como Euclides y Arquímedes estudiaron las propiedades de las cuerdas y los ángulos inscritos en círculos, y demostraron teoremas que son equivalentes a las fórmulas trigonométricas modernas, aunque las presentaron de forma geométrica en lugar de algebraica. En 140 a. C., Hiparco (de Nicea, Asia Menor) dio las primeras tablas de cuerdas, análogas a las tablas modernas de valores de senos, y las usó para resolver problemas de trigonometría y trigonometría esférica. En el siglo II d. C., el astrónomo greco-egipcio Ptolomeo (de Alejandría, Egipto) construyó tablas trigonométricas detalladas (la tabla de cuerdas de Ptolomeo) en el Libro 1, capítulo 11 de su Almagesto.Ptolomeo usó la longitud de la cuerda para definir sus funciones trigonométricas, una pequeña diferencia con la convención del seno que usamos hoy. (El valor que llamamos sin(θ) se puede encontrar buscando la longitud de la cuerda para el doble del ángulo de interés (2θ) en la tabla de Ptolomeo, y luego dividiendo ese valor por dos). Pasaron siglos antes de que se produjeran tablas más detalladas, y El tratado de Ptolomeo se mantuvo en uso para realizar cálculos trigonométricos en astronomía durante los siguientes 1200 años en los mundos medieval bizantino, islámico y, más tarde, en Europa occidental.

La convención moderna del seno se atestigua por primera vez en el Surya Siddhanta, y sus propiedades fueron documentadas más a fondo por el matemático y astrónomo indio del siglo V (d.C.) Aryabhata. Estas obras griegas e indias fueron traducidas y ampliadas por matemáticos islámicos medievales. En el siglo X, los matemáticos islámicos usaban las seis funciones trigonométricas, tabulaban sus valores y las aplicaban a problemas de geometría esférica. El erudito persa Nasir al-Din al-Tusi ha sido descrito como el creador de la trigonometría como disciplina matemática por derecho propio. Nasīr al-Dīn al-Tūsī fue el primero en tratar la trigonometría como una disciplina matemática independiente de la astronomía, y desarrolló la trigonometría esférica hasta su forma actual.Enumeró los seis casos distintos de un triángulo rectángulo en trigonometría esférica, y en su Sobre la figura del sector, estableció la ley de los senos para triángulos planos y esféricos, descubrió la ley de las tangentes para los triángulos esféricos y proporcionó pruebas para ambos. estas leyes El conocimiento de las funciones y métodos trigonométricos llegó a Europa occidental a través de las traducciones latinas del Almagesto griego de Ptolomeo, así como de los trabajos de astrónomos persas y árabes como Al Battani y Nasir al-Din al-Tusi. Uno de los primeros trabajos sobre trigonometría de un matemático del norte de Europa es De Triangulis del matemático alemán del siglo XV Regiomontanus, a quien se animó a escribir y se le proporcionó una copia del Almagesto., por el erudito griego bizantino cardenal Basilios Bessarion con quien vivió durante varios años. Al mismo tiempo, el cretense Jorge de Trebisonda completó otra traducción del Almagesto del griego al latín. La trigonometría era todavía tan poco conocida en el norte de Europa del siglo XVI que Nicolás Copérnico dedicó dos capítulos de De revolutionibus orbium coelestium a explicar sus conceptos básicos.

Impulsada por las exigencias de la navegación y la creciente necesidad de mapas precisos de grandes áreas geográficas, la trigonometría se convirtió en una rama importante de las matemáticas. Bartholomaeus Pitiscus fue el primero en usar la palabra, publicando su Trigonometria en 1595. Gemma Frisius describió por primera vez el método de triangulación que todavía se usa hoy en día en la topografía. Fue Leonhard Euler quien incorporó por completo los números complejos a la trigonometría. Los trabajos de los matemáticos escoceses James Gregory en el siglo XVII y Colin Maclaurin en el siglo XVIII influyeron en el desarrollo de las series trigonométricas. También en el siglo XVIII, Brook Taylor definió la serie general de Taylor.

Hiparco, acreditado con la compilación de la primera tabla trigonométrica , ha sido descrito como el padre de la trigonometría

Razones trigonométricas

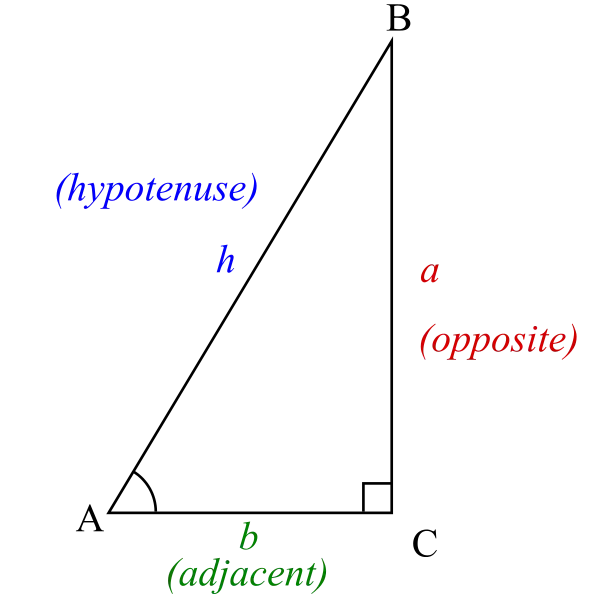
Las razones trigonométricas son las razones entre los lados de un triángulo rectángulo. Estas relaciones vienen dadas por las siguientes funciones trigonométricas del ángulo conocido A, donde a, b y h se refieren a las longitudes de los lados en la figura adjunta:

Función seno (sin), definida como la relación entre el lado opuesto al ángulo y la hipotenusa.

${displaystyle sin A={frac {textrm {opuesto}}{textrm {hipotenusa}}}={frac {a}{h}}.}$

Función coseno (cos), definida como la relación entre el cateto adyacente (el lado del triángulo que une el ángulo con el ángulo recto) y la hipotenusa.

${displaystyle cos A={frac {textrm {adyacente}}{textrm {hipotenusa}}}={frac {b}{h}}.}$

Función tangente (tan), definida como la razón del cateto opuesto al cateto adyacente.

${displaystyle tan A={frac {textrm {opuesto}}{textrm {adyacente}}}={frac {a}{b}}={frac {a/h}{b/h} }={frac {sin A}{cos A}}.}$

La hipotenusa es el lado opuesto al ángulo de 90 grados en un triángulo rectángulo; es el lado más largo del triángulo y uno de los dos lados adyacentes al ángulo A. El cateto adyacente es el otro lado adyacente al ángulo A. El lado opuesto es el lado opuesto al ángulo A. Los términos perpendicular y base a veces se usan para los lados opuestos y adyacentes respectivamente. Véase más abajo en Mnemónicos.

Dado que dos triángulos rectángulos cualesquiera con el mismo ángulo agudo A son semejantes, el valor de una razón trigonométrica depende únicamente del ángulo A.

Los recíprocos de estas funciones se denominan cosecante (csc), secante (sec) y cotangente (cot), respectivamente: ${displaystyle csc A={frac {1}{sin A}}={frac {textrm {hipotenusa}}{textrm {opuesto}}}={frac {h}{a}}, }$ ${displaystyle sec A={frac {1}{cos A}}={frac {textrm {hipotenusa}}{textrm {adyacente}}}={frac {h}{b}}, }$ $cot A={frac {1}{tan A}}={frac {{textrm {adyacente}}}{{textrm {opuesto}}}}={frac {cos A}{ sen A}}={frac {b}{a}}.$

El coseno, la cotangente y la cosecante se denominan así porque son, respectivamente, el seno, la tangente y la secante del ángulo complementario abreviado como "co-".

Con estas funciones, se pueden responder prácticamente todas las preguntas sobre triángulos arbitrarios usando la ley de los senos y la ley de los cosenos. Estas leyes se pueden usar para calcular los ángulos y lados restantes de cualquier triángulo tan pronto como se conocen dos lados y su ángulo incluido o dos ángulos y un lado o tres lados.

Mnemotécnica

Un uso común de la mnemotécnica es recordar hechos y relaciones en trigonometría. Por ejemplo, las proporciones de seno, coseno y tangente en un triángulo rectángulo se pueden recordar representándolas y sus lados correspondientes como cadenas de letras. Por ejemplo, un mnemotécnico es SOH-CAH-TOA:S ine = O ppuesto ÷ H ipotenusaCoseno = A dyacente ÷ H ipotenusaTangente = Opuesto ÷ Adyacente _

Una forma de recordar las letras es pronunciarlas fonéticamente (es decir, / ˌ s oʊ k ə ˈ t oʊ ə / SOH -kə- TOH -ə, similar a Krakatoa). Otro método es expandir las letras en una oración, como " Algún viejo hippie atrapó a otro hippie tropezando con ácido ".

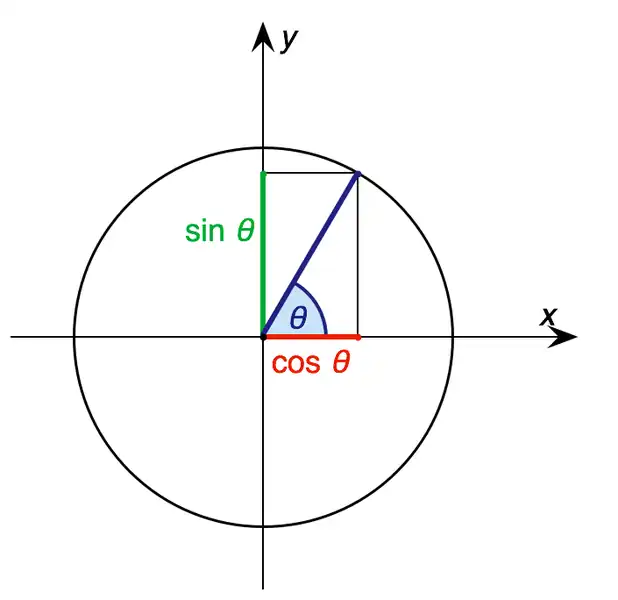
El círculo unitario y los valores trigonométricos comunes

Las razones trigonométricas también se pueden representar usando el círculo unitario, que es el círculo de radio 1 centrado en el origen en el plano. En esta configuración, el lado terminal de un ángulo A colocado en la posición estándar cortará el círculo unitario en un punto (x,y), donde ${displaystyle x=cos A}$ y ${displaystyle y=sen A}$ . Esta representación permite el cálculo de valores trigonométricos comúnmente encontrados, como los de la siguiente tabla:

Función	0	${ estilo de visualización pi /6}$	$pi /4$	$pi /3$	$pi /2$	$2pi /3$	${ estilo de visualización 3 pi /4}$	${ estilo de visualización 5 pi / 6}$	$Pi$
seno	${ estilo de visualización 0}$	$1/2$	${ sqrt {2}}/2$	${ sqrt {3}}/2$	$1$	${ sqrt {3}}/2$	${ sqrt {2}}/2$	$1/2$	${ estilo de visualización 0}$
coseno	$1$	${ sqrt {3}}/2$	${ sqrt {2}}/2$	$1/2$	${ estilo de visualización 0}$	$-1/2$	${ estilo de visualización - { sqrt {2}}/2}$	${ estilo de visualización - { sqrt {3}}/2}$	$-1$
tangente	${ estilo de visualización 0}$	${ estilo de visualización { sqrt {3}}/3}$	$1$	${ sqrt {3}}$	indefinido	$-{raíz cuadrada {3}}$	$-1$	${ estilo de visualización - { sqrt {3}}/3}$	${ estilo de visualización 0}$
secante	$1$	${ estilo de visualización 2 { sqrt {3}}/3}$	${ sqrt {2}}$	$2$	indefinido	$-2$	$-{raíz cuadrada {2}}$	${displaystyle -2{sqrt {3}}/3}$	$-1$
cosecante	indefinido	$2$	${ sqrt {2}}$	${ estilo de visualización 2 { sqrt {3}}/3}$	$1$	${ estilo de visualización 2 { sqrt {3}}/3}$	${ sqrt {2}}$	$2$	indefinido
cotangente	indefinido	${ sqrt {3}}$	$1$	${ estilo de visualización { sqrt {3}}/3}$	${ estilo de visualización 0}$	${ estilo de visualización - { sqrt {3}}/3}$	$-1$	$-{raíz cuadrada {3}}$	indefinido

Funciones trigonométricas de variables reales o complejas

Usando el círculo unitario, se pueden extender las definiciones de razones trigonométricas a todos los argumentos positivos y negativos (ver función trigonométrica).

Gráficas de funciones trigonométricas

La siguiente tabla resume las propiedades de las gráficas de las seis principales funciones trigonométricas:

Función	Período	Dominio	Distancia
seno	$2pi$	$(-infty,infty)$	$[-1,1]$
coseno	$2pi$	$(-infty,infty)$	$[-1,1]$
tangente	$Pi$	${ estilo de visualización x neq pi / 2 + n pi}$	$(-infty,infty)$
secante	$2pi$	${ estilo de visualización x neq pi / 2 + n pi}$	${displaystyle (-infty,-1]cup [1,infty)}$
cosecante	$2pi$	${ estilo de visualización x neq n pi}$	${displaystyle (-infty,-1]cup [1,infty)}$
cotangente	$Pi$	${ estilo de visualización x neq n pi}$	$(-infty,infty)$

Funciones trigonométricas inversas

Debido a que las seis funciones trigonométricas principales son periódicas, no son inyectivas (o 1 a 1) y, por lo tanto, no son invertibles. Sin embargo, al restringir el dominio de una función trigonométrica, pueden hacerse invertibles.

Los nombres de las funciones trigonométricas inversas, junto con sus dominios y rango, se pueden encontrar en la siguiente tabla:

Nombre	notación habitual	Definición	Dominio de x para resultado real	Rango de valor principal habitual(radianes)	Rango de valor principal habitual(grados)
arcoseno	y = arcosen(x)	x = sen(y)	−1 ≤ x ≤ 1	−π/2≤ y ≤π/2	−90° ≤ y ≤ 90°
arcocoseno	y = arccos(x)	x = cos(y)	−1 ≤ x ≤ 1	0 ≤ y ≤ π	0° ≤ y ≤ 180°
arcotangente	y = arco tan(x)	x = tan(y)	todos los números reales	−π/2< y <π/2	−90° < y < 90°
arcotangente	y = arccot(x)	x = cuna(y)	todos los números reales	0 < y < π	0° < y < 180°
arcosecante	y = arcosegundo(x)	x = segundo(y)	x ≤ −1 o 1 ≤ x	0 ≤ y <π/2oπ/2< y ≤ π	0° ≤ y < 90° o 90° < y ≤ 180°
arccosecante	y = arccsc(x)	x = csc(y)	x ≤ −1 o 1 ≤ x	−π/2≤ y < 0 o 0 < y ≤π/2	−90° ≤ y < 0° o 0° < y ≤ 90°

Representaciones de series de potencias

Cuando son consideradas como funciones de una variable real, las razones trigonométricas pueden ser representadas por una serie infinita. Por ejemplo, el seno y el coseno tienen las siguientes representaciones: ${displaystyle {begin{alineado}sen x&=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-{frac {x^{7}}{7!}}+cdots \&=sum _{n=0}^{infty}{frac {(-1)^{n}x^{2n+1 }}{(2n+1)!}}\end{alineado}}}$ ${displaystyle {begin{alineado}cos x&=1-{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}-{frac {x^{6}}{6!}}+cdots \&=sum _{n=0}^{infty}{frac {(-1)^{n}x^{2n}} {(2n)!}}.end{alineado}}}$

Con estas definiciones se pueden definir las funciones trigonométricas para números complejos. Cuando se extiende como funciones de variables reales o complejas, la siguiente fórmula se cumple para el exponencial complejo: ${displaystyle e^{x+iy}=e^{x}(cos y+isin y).}$

Esta función exponencial compleja, escrita en términos de funciones trigonométricas, es particularmente útil.

Cálculo de funciones trigonométricas

Las funciones trigonométricas estuvieron entre los primeros usos de las tablas matemáticas. Dichas tablas se incorporaron a los libros de texto de matemáticas y se les enseñó a los estudiantes a buscar valores y cómo interpolar entre los valores enumerados para obtener una mayor precisión. Las reglas de cálculo tenían escalas especiales para funciones trigonométricas.

Las calculadoras científicas tienen botones para calcular las principales funciones trigonométricas (sin, coseno, tangente y, a veces, cis y sus inversas). La mayoría permite una selección de métodos de medición de ángulos: grados, radianes y, a veces, gradianes. La mayoría de los lenguajes de programación de computadoras proporcionan bibliotecas de funciones que incluyen las funciones trigonométricas. El hardware de la unidad de coma flotante incorporado en los chips del microprocesador que se usa en la mayoría de las computadoras personales tiene instrucciones integradas para calcular funciones trigonométricas.

Otras funciones trigonométricas

Además de las seis proporciones enumeradas anteriormente, existen funciones trigonométricas adicionales que fueron históricamente importantes, aunque rara vez se usan en la actualidad. Estos incluyen el acorde (crd(θ) = 2 sin(θ/2)), el versine (versin (θ) = 1 − cos(θ) = 2 sin (θ/2)) (que apareció en las primeras tablas), el coversine (coversin(θ) = 1 − sin(θ) = versin(π/2− θ)), el haversine (haversen(θ) =1/2versin(θ) = sin (θ/2)), la exsecante (exsec(θ) = sec(θ) − 1), y la excosecante (excsc(θ) = exsec(π/2− θ) = csc(θ) − 1). Consulte la Lista de identidades trigonométricas para obtener más relaciones entre estas funciones.

El teorema de Pitágoras y la relación existente entre la hipotenusa y los catetos son aspectos esenciales de la trigonometría

Aplicaciones

Astronomía

Durante siglos, la trigonometría esférica se ha utilizado para ubicar posiciones solares, lunares y estelares, predecir eclipses y describir las órbitas de los planetas.

En los tiempos modernos, la técnica de la triangulación se utiliza en astronomía para medir la distancia a las estrellas cercanas, así como en los sistemas de navegación por satélite.

Navegación

Históricamente, la trigonometría se ha utilizado para ubicar latitudes y longitudes de embarcaciones de vela, trazar rumbos y calcular distancias durante la navegación.

La trigonometría todavía se usa en la navegación a través de medios como el Sistema de Posicionamiento Global y la inteligencia artificial para vehículos autónomos.

Agrimensura

En topografía, la trigonometría se utiliza en el cálculo de longitudes, áreas y ángulos relativos entre objetos.

A mayor escala, la trigonometría se usa en geografía para medir distancias entre puntos de referencia.

Funciones periódicas

Las funciones seno y coseno son fundamentales para la teoría de las funciones periódicas, como las que describen las ondas sonoras y luminosas. Fourier descubrió que toda función periódica continua podía describirse como una suma infinita de funciones trigonométricas.

Incluso las funciones no periódicas se pueden representar como una integral de senos y cosenos a través de la transformada de Fourier. Esto tiene aplicaciones en mecánica cuántica y comunicaciones, entre otros campos.

Óptica y acústica

La trigonometría es útil en muchas ciencias físicas, incluidas la acústica y la óptica. En estas áreas, se utilizan para describir las ondas de luz y sonido, y para resolver problemas relacionados con la transmisión y los límites.

Otras aplicaciones

Otros campos que utilizan la trigonometría o funciones trigonométricas incluyen teoría musical, geodesia, síntesis de audio, arquitectura, electrónica, biología, imágenes médicas (tomografías computarizadas y ultrasonido), química, teoría de números (y, por lo tanto, criptología), sismología, meteorología, oceanografía, compresión de imágenes., fonética, economía, ingeniería eléctrica, ingeniería mecánica, ingeniería civil, infografía, cartografía, cristalografía y desarrollo de juegos.

Identidades

La trigonometría se ha destacado por sus muchas identidades, es decir, ecuaciones que son verdaderas para todas las entradas posibles.

Las identidades que involucran solo ángulos se conocen como identidades trigonométricas. Otras ecuaciones, conocidas como identidades de triángulos, relacionan tanto los lados como los ángulos de un triángulo dado.

Identidades triangulares

En las siguientes identidades, A, B y C son los ángulos de un triángulo y a, b y c son las longitudes de los lados del triángulo opuestos a los ángulos respectivos (como se muestra en el diagrama).

Ley de los senos

La ley de los senos (también conocida como la "regla del seno") para un triángulo arbitrario establece: ${frac {a}{sin A}}={frac {b}{sin B}}={frac {c}{sin C}}=2R={frac {abc}{2 delta }},$

donde $Delta$ es el área del triángulo y R es el radio de la circunferencia circunscrita al triángulo: $R = frac{abc}{sqrt{(a+b+c)(a-b+c)(a+bc)(b+ca)}}.$

Ley de los cosenos

La ley de los cosenos (conocida como la fórmula del coseno o la "regla del coseno") es una extensión del teorema de Pitágoras a triángulos arbitrarios: ${displaystyle c^{2}=a^{2}+b^{2}-2abcos C,}$

o equivalente: $cos C={frac {a^{2}+b^{2}-c^{2}}{2ab}}.$

Ley de las tangentes

La ley de las tangentes, desarrollada por François Viète, es una alternativa a la Ley de los cosenos cuando se resuelven las aristas desconocidas de un triángulo, proporcionando cálculos más simples cuando se usan tablas trigonométricas. Está dado por: $frac{ab}{a+b}=frac{tanleft[tfrac{1}{2}(AB)right]}{tanleft[tfrac{1}{2}(A +B)derecho]}$

Área

Dados dos lados a y b y el ángulo entre los lados C, el área del triángulo está dada por la mitad del producto de las longitudes de dos lados por el seno del ángulo entre los dos lados:

La fórmula de Heron es otro método que puede usarse para calcular el área de un triángulo. Esta fórmula establece que si un triángulo tiene lados de longitud a, b y c, y si el semiperímetro es $s=frac{1}{2}(a+b+c),$

entonces el area del triangulo es: ${mbox{Área}}=Delta ={sqrt {s(sa)(sb)(sc)}}={frac {abc}{4R}}$ ,

donde R es el radio de la circunferencia circunscrita del triángulo. ${mbox{Área}}=Delta ={frac {1}{2}}absen C.$

Identidades trigonométricas

Identidades pitagóricas

Las siguientes identidades trigonométricas están relacionadas con el teorema de Pitágoras y se cumplen para cualquier valor: $sin^2 A + cos^2 A = 1$ $tan ^{2}A+1=sec ^{2}A$ ${displaystyle cot^{2}A+1=csc^{2}A }$

Las ecuaciones segunda y tercera se derivan de dividir la primera ecuación entre ${ estilo de visualización cos ^ {2} {A}}$ y ${ estilo de visualización sin ^ {2} {A}}$ , respectivamente.

Fórmula de Euler

La fórmula de Euler, que establece que $e^{ix} = cos x + i sin x$ , produce las siguientes identidades analíticas para seno, coseno y tangente en términos de e y la unidad imaginaria i: $sin x = frac{e^{ix} - e^{-ix}}{2i}, qquad cos x = frac{e^{ix} + e^{-ix}}{2}, qquad tan x = frac{i(e^{-ix} - e^{ix})}{e^{ix} + e^{-ix}}.$

Otras identidades trigonométricas

Otras identidades trigonométricas de uso común incluyen las identidades de medio ángulo, las identidades de suma y diferencia de ángulos y las identidades de producto a suma.

Contenido relacionado

Más resultados...