Triángulo de Pascal

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En matemáticas, el triángulo de Pascal es una matriz triangular de los coeficientes binomiales que surge en la teoría de la probabilidad, la combinatoria y el álgebra. En gran parte del mundo occidental, lleva el nombre del matemático francés Blaise Pascal, aunque otros matemáticos lo estudiaron siglos antes que él en India, Persia, China, Alemania e Italia.

Las filas del triángulo de Pascal se enumeran convencionalmente comenzando con la fila $n=0$ en la parte superior (la fila 0). Las entradas en cada fila están numeradas desde la izquierda comenzando con $k=0$ y generalmente están escalonadas en relación con los números en las filas adyacentes. El triángulo se puede construir de la siguiente manera: en la fila 0 (la fila superior), hay una única entrada distinta de cero 1. Cada entrada de cada fila subsiguiente se construye sumando el número de arriba y a la izquierda con el número de arriba y para a la derecha, tratando las entradas en blanco como 0. Por ejemplo, el número inicial en la primera (o cualquier otra) fila es 1 (la suma de 0 y 1), mientras que los números 1 y 3 en la tercera fila se suman para producir el número 4 en la cuarta fila.

Fórmula

La entrada en la $norte$ ésima fila y $k$ la ésima columna del triángulo de Pascal se denota ${n elegir k}$ . Por ejemplo, la única entrada distinta de cero en la fila superior es ${displaystyle {0 elegir 0}=1}$ . Con esta notación, la construcción del párrafo anterior puede escribirse como sigue: ${n elegir k}={n-1 elegir k-1}+{n-1 elegir k}$ ,

para cualquier entero no negativo $norte$ y cualquier entero $0leq kleq n$ . Esta recurrencia de los coeficientes binomiales se conoce como regla de Pascal.

Historia

El patrón de números que forma el triángulo de Pascal se conocía mucho antes de la época de Pascal. Pascal innovó muchos usos previamente no comprobados de los números del triángulo, usos que describió exhaustivamente en el tratado matemático más antiguo conocido dedicado especialmente al triángulo, su Traité du Triangle arithmétique (1654; publicado en 1665).

Siglos antes, la discusión sobre los números había surgido en el contexto de los estudios indios de combinatoria y números binomiales. De comentarios posteriores parece que los coeficientes binomiales y la fórmula aditiva para generarlos ${displaystyle {n elegir r}={n-1 elegir r}+{n-1 elegir r-1}}$ , eran conocidos por Pingala en o antes del siglo II a. Si bien el trabajo de Pingala solo sobrevive en fragmentos, el comentarista Varāhamihira, alrededor de 505, dio una descripción clara de la fórmula aditiva, y Halayudha dio una explicación más detallada de la misma regla, alrededor de 975. Halayudha también explicó oscuras referencias a Meru-prastaara., la Escalera del Monte Meru, dando la primera descripción sobreviviente de la disposición de estos números en un triángulo.Aproximadamente en 850, el matemático jainista Mahāvīra dio una fórmula diferente para los coeficientes binomiales, usando la multiplicación, equivalente a la fórmula moderna ${displaystyle {n elegir r}={frac {n!}{r!(nr)!}}}$ . En 1068, el matemático Bhattotpala, quien fue el primer matemático registrado en equiparar las fórmulas aditivas y multiplicativas para estos números, dio cuatro columnas de las primeras dieciséis filas.

Aproximadamente al mismo tiempo, el matemático persa Al-Karaji (953-1029) escribió un libro ahora perdido que contenía la primera descripción del triángulo de Pascal. Más tarde fue repetido por el poeta, astrónomo y matemático persa Omar Khayyám (1048-1131); por lo tanto, el triángulo también se conoce como el triángulo Khayyam en Irán. Se conocían varios teoremas relacionados con el triángulo, incluido el teorema del binomio. Khayyam usó un método para encontrar raíces enésimas basadas en la expansión binomial y, por lo tanto, en los coeficientes binomiales.

El triángulo de Pascal se conoció en China a principios del siglo XI gracias al trabajo del matemático chino Jia Xian (1010-1070). En el siglo XIII, Yang Hui (1238-1298) presentó el triángulo y, por lo tanto, todavía se le llama triángulo de Yang Hui (杨辉三角;楊輝三角) en China.

En Europa, el triángulo de Pascal apareció por primera vez en la Aritmética de Jordanus de Nemore (siglo XIII). Los coeficientes binomiales fueron calculados por Gersonides a principios del siglo XIV, utilizando para ellos la fórmula multiplicativa. Petrus Apianus (1495–1552) publicó el triángulo completo en el frontispicio de su libro sobre cálculos comerciales en 1527. Michael Stifel publicó una parte del triángulo (desde la segunda columna hasta la del medio en cada fila) en 1544, describiéndolo como un tabla de números figurados. En Italia, el triángulo de Pascal se conoce como el triángulo de Tartaglia, llamado así por el algebrista italiano Niccolò Fontana Tartaglia (1500-1577), quien publicó seis filas del triángulo en 1556.Gerolamo Cardano, también, publicó el triángulo así como las reglas aditivas y multiplicativas para construirlo en 1570.

El Traité du Triangle arithmétique de Pascal (Tratado sobre el triángulo aritmético) se publicó en 1655. En este, Pascal recopiló varios resultados conocidos entonces sobre el triángulo y los empleó para resolver problemas en la teoría de la probabilidad. Más tarde, el triángulo recibió el nombre de Pascal por Pierre Raymond de Montmort (1708), quien lo llamó "Table de M. Pascal pour les combinaisons" (en francés: Table of Mr. Pascal para combinaciones) y Abraham de Moivre (1730), quien lo llamó " Triangulum Arithmeticum PASCALIANUM" (en latín: Triángulo aritmético de Pascal), que se convirtió en el nombre occidental moderno.

Expansiones binomiales

El triángulo de Pascal determina los coeficientes que surgen en las expansiones binomiales. Por ejemplo, considere la expansión

${displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}=mathbf {1} x^{2}y^{0}+mathbf {2} x^ {1}y^{1}+mathbf {1} x^{0}y^{2}}$ .

Los coeficientes son los números en la segunda fila del triángulo de Pascal: ${displaystyle {2 elegir 0}=1}$ , ${displaystyle {2 elegir 1}=2}$ , ${displaystyle {2 elegir 2}=1}$ .

En general, cuando un binomio like $x+y$ se eleva a una potencia entera positiva de $norte$ , tenemos:

${displaystyle (x+y)^{n}=sum_{k=0}^{n}a_{k}x^{nk}y^{k}=a_{0}x^{n}+ a_{1}x^{n-1}y+a_{2}x^{n-2}y^{2}+ldots +a_{n-1}xy^{n-1}+a_{n }y^{n}}$ ,

donde los coeficientes ${displaystyle a_{k}}$ en esta expansión son precisamente los números en la fila $norte$ del triángulo de Pascal. En otras palabras, ${displaystyle a_{k}={n elegir k}}$ .

Este es el teorema del binomio.

Toda la diagonal derecha del triángulo de Pascal corresponde al coeficiente de ${displaystyle y^{n}}$ en estas expansiones binomiales, mientras que la siguiente diagonal corresponde al coeficiente de ${ estilo de visualización xy^{n-1}}$ y así sucesivamente.

Para ver cómo se relaciona el teorema del binomio con la construcción simple del triángulo de Pascal, considere el problema de calcular los coeficientes de la expansión de ${ estilo de visualización (x + y) ^ {n + 1}}$ en términos de los coeficientes correspondientes de ${ estilo de visualización (x + 1) ^ {n}}$ (estableciendo ${ estilo de visualización y = 1}$ la simplicidad). Supongamos entonces que ${displaystyle (x+1)^{n}=sum_{k=0}^{n}a_{k}x^{k}}$ .

Ahora $(x+1)^{n+1}=(x+1)(x+1)^{n}=x(x+1)^{n}+(x+1)^{n}=suma _{i=0}^{n}a_{i}x^{i+1}+sum_{i=0}^{n}a_{i}x^{i}.$

Las dos sumas se pueden reorganizar de la siguiente manera: ${displaystyle {begin{alineado}sum_{k=0}^{n}a_{k}x^{k+1}+sum_{k=0}^{n}a_{k}x ^{k}&=sum_{k=1}^{n+1}a_{k-1}x^{k}+sum_{k=0}^{n}a_{k}x^ {k}\[4pt]&=sum_{k=1}^{n}a_{k-1}x^{k}+sum_{k=1}^{n}a_{k} x^{k}+a_{0}x^{0}+a_{n}x^{n+1}\[4pt]&=sum _{k=1}^{n}(a_{k -1}+a_{k})x^{k}+a_{0}x^{0}+a_{n}x^{n+1}\[4pt]&=sum _{k=1 }^{n}(a_{k-1}+a_{k})x^{k}+x^{0}+x^{n+1}end{alineado}}}$

(por cómo funciona elevar un polinomio a una potencia, ${displaystyle a_{0}=a_{n}=1}$ ).

Ahora tenemos una expresión para el polinomio ${ estilo de visualización (x + 1) ^ {n + 1}}$ en términos de los coeficientes de ${ estilo de visualización (x + 1) ^ {n}}$ (estos son los ${displaystyle a_{k}}$ s), que es lo que necesitamos si queremos expresar una línea en términos de la línea de arriba. Recuerda que todos los términos en una diagonal que va desde la esquina superior izquierda a la esquina inferior derecha corresponden a la misma potencia de $X$ , y que los $a$ términos - son los coeficientes del polinomio ${ estilo de visualización (x + 1) ^ {n}}$ , y estamos determinando los coeficientes de ${ estilo de visualización (x + 1) ^ {n + 1}}$ . Ahora, para cualquier ${ estilo de visualización 0<k<n+1}$ , el coeficiente del ${ estilo de visualización x^{k}}$ término en el polinomio ${ estilo de visualización (x + 1) ^ {n + 1}}$ es igual a ${displaystyle a_{k-1}+a_{k}}$ . De hecho, esta es la regla simple para construir fila por fila el triángulo de Pascal.

No es difícil convertir este argumento en una demostración (por inducción matemática) del teorema del binomio.

Como ${displaystyle (a+b)^{n}=b^{n}left({frac {a}{b}}+1right)^{n}}$ , los coeficientes son idénticos en el desarrollo del caso general.

Una consecuencia interesante del teorema del binomio se obtiene igualando ambas variables $X$ a $y$ uno. En este caso, sabemos que ${ estilo de visualización (1+1)^{n}=2^{n}}$ , por lo que ${displaystyle sum _{k=0}^{n}{n elegir k}={n elegir 0}+{n elegir 1}+cdots +{n elegir n-1}+{n elegir n}=2^{n}.}$

En otras palabras, la suma de las entradas en la $norte$ fila del triángulo de Pascal es la $norte$ potencia de 2. Esto es equivalente a la afirmación de que el número de subconjuntos (la cardinalidad del conjunto de potencia) de un $norte$ conjunto de elementos es $2^{n}$ , como se puede ver observando que el número de subconjuntos es la suma del número de combinaciones de cada una de las longitudes posibles, que van desde cero hasta $norte$ .

Combinaciones

Una segunda aplicación útil del triángulo de Pascal está en el cálculo de combinaciones. Por ejemplo, el número de combinaciones de $norte$ cosas tomadas $k$ a la vez (llamadas n elige k) se puede encontrar mediante la ecuación ${displaystyle mathbf {C} (n,k)=mathbf {C} _{k}^{n}={_{n}C_{k}}={n elegir k}={frac { n!}{k!(nk)!}}}$ .

Pero esta es también la fórmula de una celda del triángulo de Pascal. En lugar de realizar el cálculo, uno puede simplemente buscar la entrada adecuada en el triángulo. Siempre que tengamos la primera fila y la primera entrada de una fila con el número 0, la respuesta se ubicará en la entrada $k$ de la fila $norte$ . Por ejemplo, supongamos que un equipo de baloncesto tiene 10 jugadores y quiere saber cuántas formas hay de seleccionar 8. La respuesta es la entrada 8 en la fila 10, que es 45; es decir, 10 elige 8 es 45.

Relación con la distribución binomial y convoluciones

Cuando se divide por $2^n$ , la $norte$ fila th del triángulo de Pascal se convierte en la distribución binomial en el caso simétrico donde ${displaystyle p={frac{1}{2}}}$ . Por el teorema del límite central, esta distribución se aproxima a la distribución normal a medida que $norte$ aumenta. Esto también se puede ver aplicando la fórmula de Stirling a los factoriales involucrados en la fórmula de las combinaciones.

Esto está relacionado con la operación de convolución discreta de dos maneras. Primero, la multiplicación de polinomios corresponde exactamente a la convolución discreta, de modo que convolucionar repetidamente la secuencia ${displaystyle {ldots,0,0,1,1,0,0,ldots}}$ consigo misma corresponde a tomar potencias de ${ estilo de visualización x+1}$ y, por lo tanto, a generar las filas del triángulo. En segundo lugar, convolucionar repetidamente la función de distribución de una variable aleatoria consigo misma corresponde a calcular la función de distribución de una suma de n copias independientes de esa variable; esta es exactamente la situación a la que se aplica el teorema del límite central y, por lo tanto, conduce a la distribución normal en el límite.

Patrones y propiedades

El triángulo de Pascal tiene muchas propiedades y contiene muchos patrones de números.

Filas

La suma de los elementos de una sola fila es el doble de la suma de la fila que la precede. Por ejemplo, la fila 0 (la fila superior) tiene un valor de 1, la fila 1 tiene un valor de 2, la fila 2 tiene un valor de 4 y así sucesivamente. Esto se debe a que cada elemento de una fila produce dos elementos en la siguiente fila: uno a la izquierda y otro a la derecha. La suma de los elementos de fila $norte$ es igual a $2^n$ .
Tomando el producto de los elementos de cada fila, la secuencia de productos (secuencia A001142 en la OEIS) se relaciona con la base del logaritmo natural, e. Específicamente, defina la secuencia ${ estilo de visualización s_ {n}}$ para todos $ngeq 0$ de la siguiente manera ${displaystyle s_{n}=prod_{k=0}^{n}{n choose k}=prod_{k=0}^{n}{frac {n!}{k!(nk)!}}}$

Entonces, la razón de los productos sucesivos de las filas es ${displaystyle {frac {s_{n+1}}{s_{n}}}={frac {displaystyle (n+1)!^{n+2}prod _{k=0}^{ n+1}{frac {1}{k!^{2}}}}{displaystyle n!^{n+1}prod _{k=0}^{n}{frac {1}{ k!^{2}}}}}={frac{(n+1)^{n}}{n!}}}$ y la razón de estas razones es ${displaystyle {frac {s_{n+1}cdot s_{n-1}}{s_{n}^{2}}}=left({frac {n+1}{n}} derecha)^{n},~ngeq 1}$ .El lado derecho de la ecuación anterior toma la forma de la definición límite de $mi$ ${displaystyle e=lim _{nto infty }left(1+{frac {1}{n}}right)^{n}}$ .

$Pi$ se puede encontrar en el triángulo de Pascal a través de la serie infinita de Nilakantha.

${displaystyle pi =3+sum _{n=1}^{infty}(-1)^{n+1}{frac {2n+1 elegir 1}{{2n+1 elegir 2 {2n+2 elegir 2}}}}$

El valor de una fila, si cada entrada se considera un lugar decimal (y los números mayores de 9 se transfieren en consecuencia), es una potencia de 11 (11, para la fila n). Así, en la fila 2, ⟨1, 2, 1⟩ se convierte en 11, mientras que ⟨1, 5, 10, 10, 5, 1⟩ en la fila cinco se convierte (después de llevar) 161,051, que es 11. Esta propiedad se explica estableciendo x = 10 en la expansión binomial de (x + 1) y ajustando los valores al sistema decimal. Pero el término variable se puede elegir para permitir que las filas representen valores en cualquier base x (más generalmente, si y = x+ 1 para y < 0, entonces la base correspondiente es x mod 2 y = { y - 1, -(y + 1) }, con valores impares de n que producen valores de fila negativos).
- En base 3: 1 2 1 ₃ = 4 (16)
- ⟨1, 3, 3, 1⟩ → 2 1 0 1 ₃ = 4 (64)
- En base 9: 1 2 1 ₉ = 10 (100)
- 1 3 3 1 ₉ = 10 (1000)
- ⟨1, 5, 10, 10, 5, 1⟩ → 1 6 2 1 5 1 ₉ = 10 (100000)
En particular (ver propiedad anterior), para x = 1 el valor posicional permanece constante (1 =1). Por lo tanto, las entradas pueden simplemente agregarse al interpretar el valor de una fila.
Algunos de los números en el triángulo de Pascal se correlacionan con números en el triángulo de Lozanić.
La suma de los cuadrados de los elementos de la fila n es igual al elemento central de la fila 2 n. Por ejemplo, 1 + 4 + 6 + 4 + 1 = 70. En forma general:

$sum _{k=0}^{n}{n elegir k}^{2}={2n elegir n}.$

En cualquier fila n, donde n es par, el término medio menos el término dos puntos a la izquierda es igual a un número catalán, específicamente el (n /2 + 1) número catalán. Por ejemplo: en la fila 4, 6 − 1 = 5, que es el 3er número catalán, y 4/2 + 1 = 3.
En una fila p donde p es un número primo, todos los términos en esa fila excepto los 1 son múltiplos de p. Esto se puede demostrar fácilmente, ya que si $pen mathbb {P}$ , entonces p no tiene factores salvo 1 y sí mismo. Cada entrada en el triángulo es un número entero, por lo tanto, por definición $(paquete)!$ y $k!$ son factores de $¡pags!,$ . Sin embargo, no hay forma posible de que p aparezca en el denominador, por lo tanto, p (o algún múltiplo de él) debe dejarse en el numerador, lo que hace que la entrada completa sea un múltiplo de p.
Paridad: para contar términos impares en la fila n, convierta n en binario. Sea x el número de 1 en la representación binaria. Entonces el número de términos impares será 2. Estos números son los valores en la secuencia de Gould.
Cada entrada en la fila 2 -1, n ≥ 0, es impar.
Polaridad: cuando los elementos de una fila del triángulo de Pascal se suman y se restan secuencialmente, cada fila con un número medio, es decir, las filas que tienen un número impar de enteros, da como resultado 0. Como ejemplos, la fila 4 es 1 4 6 4 1, por lo que la fórmula sería 6 – (4+4) + (1+1) = 0; y la fila 6 es 1 6 15 20 15 6 1, entonces la fórmula sería 20 – (15+15) + (6+6) – (1+1) = 0. Entonces cada fila par del triángulo de Pascal es igual a 0 cuando toma el número del medio, luego resta los enteros directamente al lado del centro, luego suma los siguientes enteros, luego resta, y así sucesivamente hasta llegar al final de la fila.

Diagonales

Las diagonales del triángulo de Pascal contienen los números figurados de simples:

Las diagonales que van a lo largo de los bordes izquierdo y derecho contienen solo unos.
Las diagonales al lado de las diagonales de los bordes contienen los números naturales en orden.
Moviéndose hacia adentro, el siguiente par de diagonales contiene los números triangulares en orden.
El siguiente par de diagonales contiene los números tetraédricos en orden, y el siguiente par da números de pentátopo.

${begin{alineado}P_{0}(n)&=P_{d}(0)=1,\P_{d}(n)&=P_{d}(n-1)+P_{d- 1}(n)\&=sum_{i=0}^{n}P_{d-1}(i)=sum_{i=0}^{d}P_{i}(n- 1).end{alineado}}$

La simetría del triángulo implica que el número n d-dimensional es igual al número d n -dimensional.

Una fórmula alternativa que no implica recursividad es

{displaystyle P_{d}(n)={frac {1}{d!}}prod_{k=0}^{d-1}(n+k)={n^{(d)} sobre d!}={binom {n+d-1}{d}},}

donde n es el factorial ascendente.

El significado geométrico de una función P _d es: P _d (1) = 1 para todo d. Construya un triángulo d -dimensional (un triángulo tridimensional es un tetraedro) colocando puntos adicionales debajo de un punto inicial, correspondiente a P _d (1) = 1. Coloque estos puntos de manera análoga a la colocación de números en el triángulo de Pascal. Para encontrar P _d (x), tenga un total de x puntos que compongan la forma objetivo. P _d (x) entonces es igual al número total de puntos en la forma. Un triángulo de dimensión 0 es un punto y un triángulo de dimensión 1 es simplemente una línea, y por lo tanto P ₀ (x) = 1 y P ₁ (x) = x, que es la secuencia de los números naturales. El número de puntos en cada capa corresponde a P _{d − 1} (x).

Cálculo de una fila o diagonal por sí mismo

Existen algoritmos simples para calcular todos los elementos en una fila o diagonal sin calcular otros elementos o factoriales.

Para calcular la fila $norte$ con los elementos ${tbinom {n}{0}}$ , ${tbinom {n}{1}}$ ,..., ${tbinom {n}{n}}$ , comience con ${tbinom {n}{0}}=1$ . Para cada elemento subsiguiente, el valor se determina multiplicando el valor anterior por una fracción con un numerador y un denominador que cambian lentamente: ${n elegir k}={n elegir k-1}times {frac {n+1-k}{k}}.$

Por ejemplo, para calcular la fila 5, las fracciones son ${tfrac {5}{1}}$ , ${tfrac {4}{2}}$ , y ${tfrac {3}{3}}$ , y por lo tanto los elementos son,,, etc. (Los elementos restantes se obtienen más fácilmente por simetría). ${tfrac{2}{4}}$ ${tfrac{1}{5}}$ ${tbinom {5}{0}}=1$ ${tbinom {5}{1}}=1times {tfrac {5}{1}}=5$ ${tbinom {5}{2}}=5times {tfrac {4}{2}}=10$

Para calcular la diagonal que contiene los elementos ${tbinom {n}{0}}$ , ${tbinom {n+1}{1}}$ , ${tbinom {n+2}{2}}$ ,..., comenzamos de nuevo ${tbinom {n}{0}}=1$ y obtenemos elementos subsiguientes mediante la multiplicación por ciertas fracciones: ${n+k elegir k}={n+k-1 elegir k-1}times {frac {n+k}{k}}.$

Por simetría, este mismo proceso se puede utilizar para calcular la diagonal ${tbinom {n}{n}}$ , ${displaystyle {tbinom{n+1}{n}}}$ , ${displaystyle {tbinom{n+2}{n}}}$ ....

Por ejemplo, para calcular la diagonal que comienza en ${tbinom {5}{0}}$ , las fracciones son ${tfrac {6}{1}}$ , ${tfrac {7}{2}}$ , ${tfrac {8}{3}}$ ,..., y los elementos son ${tbinom {5}{0}}=1$ , ${tbinom {6}{1}}=1times {tfrac {6}{1}}=6$ , ${tbinom {7}{2}}=6times {tfrac {7}{2}}=21$ , etc. Por simetría, estos elementos son iguales a ${tbinom {5}{5}}$ , ${tbinom {6}{5}}$ , ${tbinom {7}{5}}$ , etc.

Patrones y propiedades generales

El patrón obtenido al colorear solo los números impares en el triángulo de Pascal se parece mucho al fractal llamado triángulo de Sierpinski. Esta semejanza se vuelve más y más precisa a medida que se consideran más filas; en el límite, a medida que el número de filas se acerca al infinito, el patrón resultante es el triángulo de Sierpinski, suponiendo un perímetro fijo. Más generalmente, los números podrían colorearse de manera diferente según sean o no múltiplos de 3, 4, etc.; esto da como resultado otros patrones similares.
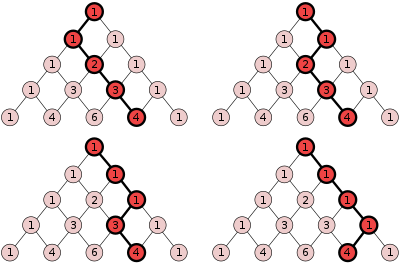
En una porción triangular de una cuadrícula (como en las imágenes a continuación), el número de rutas de cuadrícula más cortas desde un nodo determinado hasta el nodo superior del triángulo es la entrada correspondiente en el triángulo de Pascal. En un tablero de juego de Plinko con forma de triángulo, esta distribución debería dar las probabilidades de ganar los distintos premios.

Si las filas del triángulo de Pascal están justificadas a la izquierda, las bandas diagonales (codificadas por colores a continuación) suman los números de Fibonacci.

1
1	1
1	2	1
1	3	3	1
1	4	6	4	1
1	5	10	10	5	1
1	6	15	20	15	6	1
1	7	21	35	35	21	7	1

Construcción como matriz exponencial

Debido a su construcción simple por factoriales, se puede dar una representación muy básica del triángulo de Pascal en términos de la matriz exponencial: El triángulo de Pascal es la exponencial de la matriz que tiene la secuencia 1, 2, 3, 4,... en su subdiagonal y cero en todo lo demás.

Conexiones a la geometría de politopos

El triángulo de Pascal se puede usar como una tabla de búsqueda para la cantidad de elementos (como bordes y esquinas) dentro de un politopo (como un triángulo, un tetraedro, un cuadrado o un cubo).

Número de elementos de simples

Comencemos considerando la tercera línea del triángulo de Pascal, con valores 1, 3, 3, 1. Un triángulo bidimensional tiene un elemento bidimensional (en sí mismo), tres elementos unidimensionales (líneas o aristas) y tres Elementos de dimensión 0 (vértices o esquinas). El significado del número final (1) es más difícil de explicar (pero ver más abajo). Continuando con nuestro ejemplo, un tetraedro tiene un elemento tridimensional (en sí mismo), cuatro elementos bidimensionales (caras), seis elementos unidimensionales (aristas) y cuatro elementos dimensionales (vértices). Sumando nuevamente el 1 final, estos valores corresponden a la 4ª fila del triángulo (1, 4, 6, 4, 1). La línea 1 corresponde a un punto y la línea 2 corresponde a un segmento de línea (díada). Este patrón continúa con hipertetraedros de dimensiones arbitrariamente altas (conocidos como simples).

Para entender por qué existe este patrón, primero se debe entender que el proceso de construir un n -simplex a partir de un (n − 1) -simplex consiste simplemente en agregar un nuevo vértice a este último, posicionado de tal manera que este nuevo vértice quede fuera del espacio del símplex original y conectándolo a todos los vértices originales. Como ejemplo, considere el caso de construir un tetraedro a partir de un triángulo, el último de cuyos elementos están enumerados por la fila 3 del triángulo de Pascal: 1 cara, 3 aristas y 3vértices (el significado del 1 final se explicará en breve). Para construir un tetraedro a partir de un triángulo, colocamos un nuevo vértice sobre el plano del triángulo y conectamos este vértice a los tres vértices del triángulo original.

El número de un elemento dimensional dado en el tetraedro es ahora la suma de dos números: primero el número de ese elemento que se encuentra en el triángulo original, más el número de elementos nuevos, cada uno de los cuales se construye sobre elementos de una dimensión menos del triángulo original. triángulo primitivo. Así, en el tetraedro, el número de celdas (elementos poliédricos) es 0 + 1 = 1; el número de caras es 1 + 3 = 4; el número de aristas es 3 + 3 = 6; el número de nuevos vértices es 3 + 1 = 4. Este proceso de sumar el número de elementos de una dimensión dada a los de una dimensión menos para llegar al número de los primeros que se encuentra en el símplex inmediatamente superior es equivalente al proceso de sumar dos números adyacentes en una fila del triángulo de Pascal para obtener el número de abajo. Por lo tanto, el significado del número final (1) en una fila del triángulo de Pascal se entiende como la representación del nuevo vértice que se agregará al símplex representado por esa fila para producir el siguiente símplex superior representado por la siguiente fila. Este nuevo vértice se une a cada elemento del símplex original para producir un nuevo elemento de una dimensión más alta en el nuevo símplex, y este es el origen del patrón que se encuentra idéntico al que se ve en el triángulo de Pascal. El 1 "extra" en una fila se puede considerar como el -1 simplex,

Número de elementos de hipercubos

Se observa un patrón similar en relación con los cuadrados, a diferencia de los triángulos. Para encontrar el patrón, se debe construir un análogo al triángulo de Pascal, cuyas entradas son los coeficientes de (x + 2), en lugar de (x + 1). Hay un par de maneras de hacer esto. Lo más simple es comenzar con Fila 0 = 1 y Fila 1 = 1, 2. Proceda a construir los triángulos analógicos de acuerdo con la siguiente regla: ${n elegir k}=2times {n-1 elegir k-1}+{n-1 elegir k}.$

Es decir, elige un par de números según las reglas del triángulo de Pascal, pero duplica el de la izquierda antes de sumar. Esto resulta en: ${displaystyle {begin{matriz}{text{ 1}}\{text{ 1}}quad {text{ 2}}\{text{ 1}}quad {text{ 4 }}quad {text{ 4}}\{text{ 1}}quad {text{ 6}}quad {text{ 12}}quad {text{ 8}}\{ text{ 1}}quad {text{ 8}}quad {text{ 24}}quad {text{ 32}}quad {text{ 16}}\{text{ 1} }quad {text{ 10}}quad {text{ 40}}quad {text{ 80}}quad {text{ 80}}quad {text{ 32}}\{ texto{ 1}}quad {text{ 12}}quad {text{ 60}}quad 160quad 240quad 192quad {text{ 64}}\{text{ 1}} quad {text{ 14}}quad {text{ 84}}quad 280quad 560quad 672quad 448quad 128end{matriz}}}$

La otra forma de fabricar este triángulo es comenzar con el triángulo de Pascal y multiplicar cada entrada por 2, donde k es la posición en la fila del número dado. Por ejemplo, el segundo valor en la fila 4 del triángulo de Pascal es 6 (la pendiente de 1 corresponde a la entrada cero en cada fila). Para obtener el valor que reside en la posición correspondiente en el triángulo analógico, multiplique 6 por 2 = 6 × 2 = 6 × 4 = 24. Ahora que se ha construido el triángulo analógico, el número de elementos de cualquier dimensión que componen un cubo de dimensiones arbitrarias (llamado hipercubo) se puede leer en la tabla de forma análoga al triángulo de Pascal. Por ejemplo, el número de elementos de 2 dimensiones en un cubo de 2 dimensiones (un cuadrado) es uno, el número de elementos de 1 dimensión (lados o líneas) es 4 y el número de elementos de 0 dimensiones (puntos, o vértices) es 4. Esto coincide con la segunda fila de la tabla (1, 4, 4). Un cubo tiene 1 cubo, 6 caras, 12 aristas y 8 vértices, que corresponde a la siguiente línea del triángulo analógico (1, 6, 12, 8). Este patrón continúa indefinidamente.

Para comprender por qué existe este patrón, primero reconozca que la construcción de un cubo n a partir de un cubo (n − 1) se realiza simplemente duplicando la figura original y desplazándola cierta distancia (para un cubo regular n, la longitud de la arista) ortogonal al espacio de la figura original, conectando luego cada vértice de la nueva figura con su vértice correspondiente de la original. Este proceso de duplicación inicial es la razón por la cual, para enumerar los elementos dimensionales de un cubo de n, uno debe duplicar el primero de un par de números en una fila de este análogo del triángulo de Pascal antes de sumar para obtener el número a continuación. La duplicación inicial da por tanto el número de elementos "originales" que se encontrarán en el siguiente elemento superior.n -cubo y, como antes, se construyen nuevos elementos sobre los de una dimensión menos (aristas sobre vértices, caras sobre aristas, etc.). Nuevamente, el último número de una fila representa el número de nuevos vértices que se agregarán para generar el próximo cubo n superior.

En este triángulo, la suma de los elementos de la fila m es igual a 3. De nuevo, para usar los elementos de la fila 4 como ejemplo: 1 + 8 + 24 + 32 + 16 = 81, que es igual a $3^{4}=81$ .

Contar vértices en un cubo por distancia

Cada fila del triángulo de Pascal da el número de vértices a cada distancia de un vértice fijo en un cubo de n dimensiones. Por ejemplo, en tres dimensiones, la tercera fila (1 3 3 1) corresponde al cubo tridimensional habitual: fijando un vértice V, hay un vértice a la distancia 0 de V (es decir, V mismo), tres vértices a distancia 1, tres vértices a distancia √ 2 y un vértice a distancia √ 3 (el vértice opuesto a V). La segunda fila corresponde a un cuadrado, mientras que las filas con números más grandes corresponden a hipercubos en cada dimensión.

Transformada de Fourier de sin(x) / x

Como se indicó anteriormente, los coeficientes de (x + 1) son la n-ésima fila del triángulo. Ahora los coeficientes de (x − 1) son los mismos, excepto que el signo alterna de +1 a −1 y viceversa. Después de una normalización adecuada, el mismo patrón de números ocurre en la transformada de Fourier de sen(x) / x. Más precisamente: si n es par, toma la parte real de la transformada, y si n es impar, toma la parte imaginaria. Entonces el resultado es una función escalonada, cuyos valores (adecuadamente normalizados) vienen dados por la n -ésima fila del triángulo con signos alternos. Por ejemplo, los valores de la función de paso que resulta de: $,{mathfrak {Re}}left({text{Fourier}}left[{frac {sin(x)^{5}}{x}}right]right)$

componen la 4ª fila del triángulo, con signos alternos. Esta es una generalización del siguiente resultado básico (a menudo utilizado en ingeniería eléctrica): $,{mathfrak {Re}}left({text{Fourier}}left[{frac {sin(x)^{1}}{x}}right]right)$

es la función furgón. La fila correspondiente del triángulo es la fila 0, que consiste solo en el número 1.

Si n es congruente con 2 o con 3 mod 4, entonces los signos comienzan con −1. De hecho, la secuencia de los primeros términos (normalizados) corresponde a las potencias de i, que giran alrededor de la intersección de los ejes con el círculo unitario en el plano complejo: $,+i,-1,-i,+1,+i,ldots,$

Extensiones

A dimensiones superiores

El triángulo de Pascal tiene generalizaciones dimensionales superiores. La versión tridimensional se denomina pirámide de Pascal o tetraedro de Pascal, mientras que las versiones generales se denominan simples de Pascal.

Filas con numeración negativa

El triángulo de Pascal se puede extender a números de fila negativos.

Primero escribe el triángulo de la siguiente forma:

metronorte	0	1	2	3	4	...
0	1	0	0	0	0	...
1	1	1	0	0	0	...
2	1	2	1	0	0	...
3	1	3	3	1	0	...
4	1	4	6	4	1	...

A continuación, extienda la columna de 1s hacia arriba:

metronorte	0	1	2	3	4	5	...
−4	1						...
−3	1						...
−2	1						...
−1	1						...
0	1	0	0	0	0	0	...
1	1	1	0	0	0	0	...
2	1	2	1	0	0	0	...
3	1	3	3	1	0	0	...
4	1	4	6	4	1	0	...

Ahora la regla: ${n elegir m}={n-1 elegir m-1}+{n-1 elegir m}$

se puede reorganizar para: ${n-1 elegir m}={n elegir m}-{n-1 elegir m-1}$

que permite el cálculo de las otras entradas para filas negativas:

metronorte	0	1	2	3	4	5	...
−4	1	−4	10	−20	35	−56	...
−3	1	−3	6	−10	15	−21	...
−2	1	−2	3	−4	5	−6	...
−1	1	−1	1	−1	1	−1	...
0	1	0	0	0	0	0	...
1	1	1	0	0	0	0	...
2	1	2	1	0	0	0	...
3	1	3	3	1	0	0	...
4	1	4	6	4	1	0	...

Esta extensión conserva la propiedad de que los valores en la m -ésima columna vistos como una función de n se ajustan a un polinomio de orden m, a saber ${n elegir m}={frac {1}{m!}}prod _{k=0}^{m-1}(nk)={frac {1}{m!}}prod _ {k=1}^{m}(n-k+1)$ .

Esta extensión también conserva la propiedad de que los valores en la n -ésima fila corresponden a los coeficientes de (1 + x): $(1+x)^{n}=sum _{k=0}^{infty}{n elegir k}x^{k}quad |x|<1$

Por ejemplo: $(1+x)^{-2}=1-2x+3x^{2}-4x^{3}+cdotsquad |x|<1$

Cuando se ve como una serie, las filas de n negativa divergen. Sin embargo, todavía son sumables de Abel, cuya suma da los valores estándar de 2. (De hecho, la fila n = -1 da como resultado la serie de Grandi que "suma" a 1/2, y la fila n = -2 da como resultado otra serie conocida que tiene una suma de Abel de 1/4).

Otra opción para extender el triángulo de Pascal a filas negativas es extender la otra línea de 1:

metronorte	−4	−3	−2	−1	0	1	2	3	4	...
−4	1	0	0	0	0	0	0	0	0	...
−3		1	0	0	0	0	0	0	0	...
−2			1	0	0	0	0	0	0	...
−1				1	0	0	0	0	0	...
0	0	0	0	0	1	0	0	0	0	...
1	0	0	0	0	1	1	0	0	0	...
2	0	0	0	0	1	2	1	0	0	...
3	0	0	0	0	1	3	3	1	0	...
4	0	0	0	0	1	4	6	4	1	...

La aplicación de la misma regla que antes conduce a

metronorte	−4	−3	−2	−1	0	1	2	3	4	...
−4	1	0	0	0	0	0	0	0	0	...
−3	−3	1	0	0	0	0	0	0	0	...
−2	3	−2	1	0	0	0	0	0	0	...
−1	−1	1	−1	1	0	0	0	0	0	..
0	0	0	0	0	1	0	0	0	0	...
1	0	0	0	0	1	1	0	0	0	...
2	0	0	0	0	1	2	1	0	0	...
3	0	0	0	0	1	3	3	1	0	...
4	0	0	0	0	1	4	6	4	1	...

Esta extensión también tiene las propiedades de que al igual que $exp {begin{pmatrix}.&.&.&.&.\1&.&.&.&.\.&2&.&.&.\.&.&3&.&.\.&. &.&4&.end{pmatrix}}={begin{pmatrix}1&.&.&.&.\1&1&.&.&.\1&2&1&.&.\1&3&3&1&.\1&4&6&4&1end{pmatrix }},$

tenemos $exp {begin{pmatrix}.&.&.&.&.&.&.&.&.&.\-4&.&.&.&.&.&.&.&.&.\.&-3&.&.&.&.&.&.&.&.\.&.&-2&.&.&.&.&.&.&.\.&.&.&-1&.&.&.&.&.&.\.&.&.&.&0&.&.&.&.&.\.&.&.&.&.&1&.&.&.&. .&.&.&.&.&.&2&.&.&.\.&.&.&.&.&.&.&3&.&.\.&.&.&.&.&. &.&.&4&.end{pmatrix}}={begin{pmatrix}1&.&.&.&.&.&.&.&.&.\-4&1&.&.&.&.&. &.&.&.\6&-3&1&.&.&.&.&.&.&.\-4&3&-2&1&.&.&.&.&.&.\1&-1&1&-1&1&.&.&.&.&.\.&.&.&.&.&1&.&.&.&.\.&.&.&.&.&1&1&.&. &.\.&.&.&.&.&1&2&1&.&.\.&.&.&.&.&1&3&3&1&.\.&.&.&.&.&1&4&6&4&1end{pmatrix}}$

Además, al igual que sumar a lo largo de las diagonales inferior izquierda a superior derecha de la matriz de Pascal produce los números de Fibonacci, este segundo tipo de extensión todavía suma los números de Fibonacci para el índice negativo.

Cualquiera de estas extensiones se puede alcanzar si definimos ${n elegir k}={frac {n!}{(nk)!k!}}equiv {frac {Gamma (n+1)}{Gamma (n-k+1)Gamma (k+1)}}$

y tomar ciertos límites de la función gamma, $gamma (z)$ .

Contenido relacionado

Más resultados...