Triangulación

Punto de triangulación firmado por varilla de hierro

En trigonometría y geometría, la triangulación es el proceso de determinar la ubicación de un punto formando triángulos hasta el punto a partir de puntos conocidos.

Aplicaciones

Encontrar la posición de un objeto distante B con los ángulos observados desde los puntos A y C y la base b entre ellos

En topografía

Específicamente en topografía, la triangulación implica solo mediciones de ángulos en puntos conocidos, en lugar de medir distancias al punto directamente como en la trilateración; el uso de mediciones tanto de ángulos como de distancias se conoce como triangulación.

En visión artificial

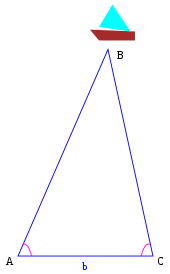
Los sistemas de medición 3D ópticos y de visión estéreo por computadora utilizan este principio para determinar las dimensiones espaciales y la geometría de un elemento. Básicamente, la configuración consta de dos sensores que observan el artículo. Uno de los sensores suele ser un dispositivo de cámara digital y el otro también puede ser una cámara o un proyector de luz. Los centros de proyección de los sensores y el punto considerado en la superficie del objeto definen un triángulo (espacial). Dentro de este triángulo, la distancia entre los sensores es la base b y debe conocerse. Al determinar los ángulos entre los rayos de proyección de los sensores y la base, se calcula el punto de intersección y, por lo tanto, la coordenada 3D a partir de las relaciones triangulares.

Historia

Medición de la altura de un edificio con un inclinador

Hoy en día, la triangulación se utiliza para muchos propósitos, incluidos la topografía, la navegación, la metrología, la astrometría, la visión binocular, los modelos de cohetes y, en el ámbito militar, la dirección del arma, la trayectoria y la distribución de la potencia de fuego de las armas.

El uso de triángulos para estimar distancias data de la antigüedad. En el siglo VI a. C., unos 250 años antes del establecimiento de la dinastía ptolemaica, se registra que el filósofo griego Tales usó triángulos similares para estimar la altura de las pirámides del antiguo Egipto. Midió la longitud de las pirámides' sombras y la suya en el mismo momento, y comparó las proporciones con su altura (teorema del intercepto). Thales también estimó las distancias a los barcos en el mar vistos desde la cima de un acantilado midiendo la distancia horizontal atravesada por la línea de visión para una caída conocida y escalando hasta la altura de todo el acantilado. Tales técnicas habrían sido familiares para los antiguos egipcios. El problema 57 del papiro Rhind, mil años antes, define el seqt o seked como la relación entre la carrera y la subida de una pendiente, es decir el recíproco de los gradientes medidos hoy. Las pendientes y los ángulos se midieron con una mira que los griegos llamaban dioptra, precursora de la alidada árabe. Se conoce una colección contemporánea detallada de construcciones para la determinación de longitudes a distancia utilizando este instrumento, la Dioptra de Héroe de Alejandría (c. 10-70 d. C.), que sobrevivió en traducción al árabe; pero el conocimiento se perdió en Europa hasta que en 1615 Snellius, después del trabajo de Eratóstenes, reelaboró la técnica para intentar medir la circunferencia de la tierra. En China, Pei Xiu (224–271) identificó "medir ángulos rectos y ángulos agudos" como el quinto de sus seis principios para la elaboración de mapas precisos, necesarios para establecer distancias con precisión, mientras que Liu Hui (c. 263) da una versión del cálculo anterior, para medir distancias perpendiculares a lugares inaccesibles.