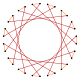
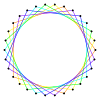Triacontagono
En geometría, una Triacontagon o 30-gon es un polígono de treinta lados. La suma de los ángulos interiores de cualquier triacongono es de 5040 grados.
Triacontagonismo regular
El regular triacontagonismo es un polígono constructible, por un borde-bisección de un pentadecagón regular, y también se puede construir como un pentadecagón t{15}. Un trícongono truncado, t{30}, es un hexacontágono, {60}.
Un ángulo interior en un triacotágono regular es de 168 grados, lo que significa que un ángulo exterior sería de 12°. El triacontagono es el polígono regular más grande cuyo ángulo interior es la suma de los ángulos interiores de polígonos más pequeños: 168° es la suma de los ángulos interiores del triángulo equilátero (60°) y el pentágono regular (108°).
El área de un triacontagono regular es (con t = longitud del borde)
El inradio de un triacontagono regular es
El circunradio de un triacontagono regular es
Construcción
AS 30 = 2 × 3 × 5 Un triacontagon regular es construcible utilizando una brújula y una regla.
simetría
La triacontagon regular tiene dih 30 simetría diédrica, orden 60, representada por 30 líneas de reflexión. DIH 30 tiene 7 subgrupos diédricos: dih 15 , (dih 10 , dih 5 ), (dih 6 , DIH 3 ), y (Dih 2 , DIH 1 ). También tiene ocho simetrías cíclicas más como subgrupos: (z 30 , z 15 ), (z 10 , z 5 ), (z 6 , z 3 ) y (z 2 , z 1 ), con Z N Representando π/ n simetría rotacional radiana.
John Conway etiqueta estas simetrías más bajas con una letra y el orden de la simetría sigue la letra. Da d (diagonal) con líneas de espejo a través de vértices, p con líneas de espejo a través de bordes (perpendiculares), i con líneas de espejo a través de ambos vértices y bordes, y g para simetría rotacional. a1 no etiqueta la simetría.
Estas simetrías más bajas permiten grados de libertades en la definición de triacontagones irregulares. Solo el subgrupo g30 no tiene grados de libertad, pero puede verse como bordes dirigidos.
disección
Coxeter afirma que cada zonogon (un 2m-gon cuyos lados opuestos son paralelos y de igual longitud) se puede diseccionar en m(m-1)/2 paralelogramos. En particular, esto es cierto para los polígonos regulares con el mismo número de lados, en cuyo caso todos los paralelogramos son rombos. Para el triacontagon regular, m=15, se puede dividir en 105: 7 conjuntos de 15 rombos. Esta descomposición se basa en una proyección del polígono de Petrie de un cubo de 15.
 |  |  |  |  |
Triacontagrama
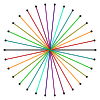
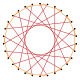
Un triacontagrama es un polígono estrella de 30 caras (aunque la palabra es extremadamente rara). Hay 3 formas regulares dadas por los símbolos Schläfli {30/7}, {30/11}, y {30/13}, y 11 figuras de estrellas compuestas con la misma configuración del vértice.
| Compuestos y estrellas | |||||||
|---|---|---|---|---|---|---|---|
| Formulario | Compuestos | Pológono estrella | Compuesto | ||||
| Imagen | .svg) {30/2}=2{15} | .svg) {30/3}=3{10} | .svg) {30/4}=2{15/2} | .svg) {30/5}=5{6} | .svg) {30/6}=6{5} |  {30/7} | .svg) {30/8}=2{15/4} |
| Ángulo interior | 156° | 144° | 132° | 120° | 108° | 96° | 84° |
| Formulario | Compuestos | Pológono estrella | Compuesto | Pológono estrella | Compuestos | ||
| Imagen | .svg) {30/9}=3{10/3} | .svg) {30/10}=10{3} |  {30/11} | .svg) {30/12}=6{5/2} |  {30/13} | .svg) {30/14}=2{15/7} | .svg) {30/15}=15{2} |
| Ángulo interior | 72° | 60° | 48° | 36° | 24° | 12° | 0° |
También hay triacontagramas isogonales construidos como truncamientos más profundos del pentadecágono regular {15} y del pentadecagrama {15/7}, y pentadecagramas invertidos {15/11} y {15/13}. Otros truncamientos forman coberturas dobles: t{15/14}={30/14}=2{15/7}, t{15/8}={30/8}=2{15/4}, t{15/ 4}={30/4}=2{15/4} y t{15/2}={30/2}=2{15}.
| Compuestos y estrellas | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Quasiregular | Isogonal | Quasiregular Cubrimientos dobles | |||||||||
 t{15} = {30} |  |  |  |  |  |  |  |  t{15/14}=2{15/7} | |||
 t{15/7}={30/7} |  |  |  |  |  |  |  |  t{15/8}=2{15/4} | |||
 t{15/11}={30/11} |  |  |  |  |  |  |  |  t{15/4}=2{15/2} | |||
 t{15/13}={30/13} |  |  |  |  |  |  |  |  t{15/2}=2{15} | |||
Polígonos de Petrie
El triacontagono regular es el polígono de Petrie para tres politopos de 8 dimensiones con simetría E8, que se muestran en proyecciones ortogonales en el plano E8 de Coxeter. También es el polígono de Petrie para dos politopos de 4 dimensiones, que se muestran en el plano H4 Coxeter.
| E8 | H4 | |||
|---|---|---|---|---|
 421 |  241 | 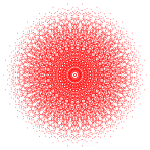 142 |  120 celdas | 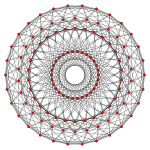 600 celdas |
El triacontagrama regular {30/7} es también el polígono Petrie para el gran estelar 120 células y grandes 600 células.