Trazado de rayos (gráficos)

Esta búsqueda de rayos recursivos de esferas de color reflexiva en una superficie blanca demuestra los efectos de profundidad poco profunda de campo, fuentes de luz "área", e interreflexión difusa.

En gráficos 3D por computadora, trazado de rayos es una técnica para modelar el transporte de luz para su uso en una amplia variedad de algoritmos de renderizado para generar imágenes digitales.

En un espectro de costo computacional y fidelidad visual, las técnicas de renderizado basadas en trazado de rayos, como el trazado de rayos, el trazado de rayos recursivo, el trazado de rayos de distribución, el mapeo de fotones y el trazado de rutas, son generalmente más lentas y de mayor fidelidad que los métodos de renderizado de línea de exploración. Por lo tanto, el trazado de rayos se implementó por primera vez en aplicaciones en las que se podía tolerar un tiempo relativamente largo para renderizar, como en imágenes fijas generadas por computadora y efectos visuales (VFX) de películas y televisión, pero era menos adecuado para aplicaciones en tiempo real como como videojuegos, donde la velocidad es fundamental para renderizar cada fotograma.

Sin embargo, desde 2018, la aceleración de hardware para el trazado de rayos en tiempo real se ha convertido en un estándar en las nuevas tarjetas gráficas comerciales, y las API de gráficos han seguido su ejemplo, lo que permite a los desarrolladores usar el trazado de rayos híbrido y la representación basada en rasterización en juegos y otros entornos reales. aplicaciones de tiempo con un menor impacto en los tiempos de procesamiento de fotogramas.

El trazado de rayos es capaz de simular una variedad de efectos ópticos, como reflexión, refracción, sombras suaves, dispersión, profundidad de campo, desenfoque de movimiento, cáusticos, oclusión ambiental y fenómenos de dispersión (como la aberración cromática). También se puede usar para rastrear el camino de las ondas de sonido de manera similar a las ondas de luz, lo que lo convierte en una opción viable para un diseño de sonido más inmersivo en los videojuegos al generar reverberaciones y ecos realistas. De hecho, cualquier fenómeno físico de onda o partícula con movimiento aproximadamente lineal puede simularse con el trazado de rayos.

Las técnicas de representación basadas en el trazado de rayos que implican el muestreo de luz sobre un dominio generan artefactos de ruido de imagen que se pueden abordar mediante el seguimiento de una gran cantidad de rayos o mediante técnicas de eliminación de ruido.

Historia

Este corte de madera de Albrecht Dürer de 1525 muestra el uso de la puerta de un Durero.

Esta imagen de Albrecht Dürer de 1532 muestra a un hombre usando un diseño de rejilla para crear una imagen. El artista alemán de renacimiento se acredita con la primera descripción de la técnica.

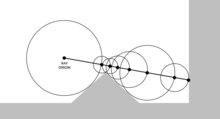
La idea del trazado de rayos se remonta al siglo XVI, cuando fue descrito por Albrecht Dürer, a quien se le atribuye su invención. En Cuatro libros sobre medidas, describió un aparato llamado Puerta de Durero que usa un hilo unido al extremo de un lápiz óptico que un asistente mueve a lo largo de los contornos del objeto a dibujar. El hilo pasa por el marco de la puerta y luego por un gancho en la pared. El hilo forma un rayo y el gancho actúa como centro de proyección y corresponde a la posición de la cámara en el trazado de rayos.

El uso de una computadora para el trazado de rayos para generar imágenes sombreadas fue realizado por primera vez por Arthur Appel en 1968. Appel usó el trazado de rayos para la visibilidad primaria (determinando la superficie más cercana a la cámara en cada punto de la imagen) y rastreó los rayos secundarios a la luz. fuente de cada punto sombreado para determinar si el punto estaba en la sombra o no.

Más tarde, en 1971, Goldstein y Nagel de MAGI (Mathematical Applications Group, Inc.) publicaron "Simulación visual en 3D", en la que se utiliza el trazado de rayos para crear imágenes sombreadas de sólidos simulando el proceso fotográfico a la inversa. Proyectan un rayo a través de cada elemento de imagen (píxel) en la pantalla hacia la escena para identificar la superficie visible. La primera superficie cortada por el rayo fue la visible. Este algoritmo de renderizado basado en trazado de rayos no recursivo se llama hoy "ray casting". En el punto de intersección de la superficie del rayo encontrado, calcularon la superficie normal y, conociendo la posición de la fuente de luz, calcularon el brillo del píxel en la pantalla. Su publicación describe una película corta (30 segundos) “realizada con el hardware de visualización de la Universidad de Maryland equipado con una cámara de 16 mm. La película mostraba el helicóptero y un simple emplazamiento de armas a nivel del suelo. El helicóptero fue programado para realizar una serie de maniobras que incluyen giros, despegues y aterrizajes, etc., hasta que finalmente es derribado y estrellado”. Se utilizó una computadora CDC 6600. MAGI produjo un video de animación llamado MAGI/SynthaVision Sampler en 1974.

Libro Flip creado en 1976 en Caltech

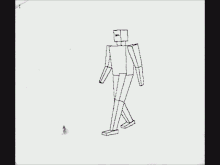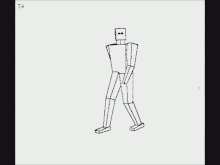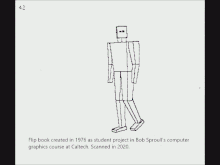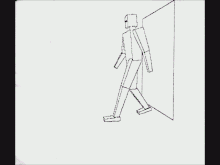
Otro ejemplo temprano de emisión de rayos se produjo en 1976, cuando Scott Roth creó una animación de libro animado en el curso de gráficos por computadora de Bob Sproull en Caltech. Las páginas escaneadas se muestran como un video a la derecha. El programa de computadora de Roth notó un punto de borde en una ubicación de píxel si el rayo intersecaba un plano acotado diferente al de sus vecinos. Por supuesto, un rayo podría intersectar múltiples planos en el espacio, pero solo el punto de la superficie más cercano a la cámara se notó como visible. Los bordes son irregulares porque solo una resolución gruesa era práctica con el poder de cómputo del DEC PDP-10 de tiempo compartido utilizado. El "terminal" era una pantalla de tubo de almacenamiento Tektronix para texto y gráficos. Adjunto a la pantalla había una impresora que crearía una imagen de la pantalla en papel térmico enrollable. Roth amplió el marco, introdujo el término proyección de rayos en el contexto de gráficos por computadora y modelado sólido, y luego publicó su trabajo mientras trabajaba en GM Research Labs.

Turner Whitted fue el primero en mostrar el trazado de rayos recursivo para la reflexión de espejos y la refracción a través de objetos translúcidos, con un ángulo determinado por el índice de refracción del sólido, y en utilizar el trazado de rayos para el suavizado. Whitted también mostró sombras trazadas por rayos. Produjo una película con trazado de rayos recursivo llamada The Compleat Angler en 1979 cuando era ingeniero en Bell Labs. El algoritmo de trazado de rayos profundamente recursivo de Whitted reformuló el renderizado de ser principalmente una cuestión de determinación de la visibilidad de la superficie a ser una cuestión de transporte ligero. Su artículo inspiró una serie de trabajos posteriores de otros que incluyeron el trazado de rayos de distribución y, finalmente, el trazado de ruta imparcial, que proporciona el marco de la ecuación de representación que ha permitido que las imágenes generadas por computadora sean fieles a la realidad.

Durante décadas, la iluminación global en las principales películas que usaban imágenes generadas por computadora se falsificó con luces adicionales. El renderizado basado en el trazado de rayos eventualmente cambió eso al permitir el transporte ligero basado físicamente. Los primeros largometrajes renderizados en su totalidad mediante el trazado de rutas incluyen Monster House (2006), Cloudy with a Chance of Meatballs (2009) y Monsters University (2013).

Resumen del algoritmo

El algoritmo de trazado de rayos construye una imagen extendiendo los rayos en una escena y rebotando de superficies y hacia fuentes de luz para aproximar el valor de color de los píxeles.

Ilustración del algoritmo de localización de rayos para un píxel (hasta el primer rebote)

El trazado de rayos ópticos describe un método para producir imágenes visuales construidas en entornos de gráficos por computadora en 3D, con más fotorrealismo que las técnicas de proyección de rayos o de representación de líneas de exploración. Funciona trazando un camino desde un ojo imaginario a través de cada píxel en una pantalla virtual y calculando el color del objeto visible a través de él.

Las escenas en trazado de rayos son descritas matemáticamente por un programador o un artista visual (normalmente usando herramientas intermedias). Las escenas también pueden incorporar datos de imágenes y modelos capturados por medios como la fotografía digital.

Normalmente, cada rayo debe probarse para la intersección con algún subconjunto de todos los objetos en la escena. Una vez que se haya identificado el objeto más cercano, el algoritmo estimará la luz entrante en el punto de intersección, examinará las propiedades materiales del objeto y combinará esta información para calcular el color final del píxel. Ciertos algoritmos de iluminación y materiales reflectantes o translúcidos pueden requerir que se reproyecten más rayos en la escena.

Al principio puede parecer contradictorio o "al revés" para enviar rayos lejos de la cámara, en lugar de dentro de ella (como lo hace la luz real en la realidad), pero hacerlo es muchos órdenes de magnitud más eficiente. Dado que la gran mayoría de los rayos de luz de una fuente de luz dada no llegan directamente al ojo del espectador, un 'hacia adelante' la simulación podría potencialmente desperdiciar una gran cantidad de cómputo en caminos de luz que nunca se registran.

Por lo tanto, el atajo tomado en el trazado de rayos es presuponer que un rayo dado intersecta el marco de la vista. Después de un número máximo de reflejos o un rayo que viaja una cierta distancia sin intersección, el rayo deja de viajar y el valor del píxel se actualiza.

Calcular rayos para ventana rectangular

En la entrada tenemos (en el cálculo usamos la normalización vectorial y el producto cruzado):

• E▪ ▪ R3{displaystyle Ein mathbb {R^{3} posición del ojo
• T▪ ▪ R3{displaystyle Tin mathbb {R^{3} de destino
• Silencio Silencio ▪ ▪ [0,π π ]{displaystyle theta in [0,pi]} campo de visión - para los humanos, podemos asumir .. π π /2rad=90∘ ∘ {displaystyle approx pi /2{text{ rad}=90^{circ }
• m,k▪ ▪ N{displaystyle m,kin mathbb {N} números de píxeles cuadrados en dirección vertical y horizontal
• i,j▪ ▪ N,1≤ ≤ i≤ ≤ k∧ ∧ 1≤ ≤ j≤ ≤ m{displaystyle i,jin mathbb {N}1leq ileq kland 1leq jleq m} números de píxel real
• v→ → ▪ ▪ R3{displaystyle {vec {fn}en mathbb {R^{3}} vector vertical que indica dónde está arriba y abajo, generalmente v→ → =[0,1,0]{displaystyle {vec {}=[0,0]} (no visible en la imagen) - componente de rollo que determina la rotación del puerto alrededor del punto C (donde el eje de rotación es la sección ET)

La idea es encontrar la posición de cada centro de pixel viewport Pij{displaystyle P_{ij} que nos permite encontrar la línea que va del ojo E{displaystyle E} a través de ese pixel y finalmente conseguir el rayo descrito por punto E{displaystyle E} vector R→ → ij=Pij− − E{displaystyle {vec {R}_{ij}=P_{ij}-E} (o su normalización r→ → ij{displaystyle {vec}_{ij}}). Primero tenemos que encontrar las coordenadas de la parte inferior izquierda del mirador pixel P1m{displaystyle P_{1m} y encontrar el próximo píxel haciendo un cambio a lo largo de las direcciones paralelas al puerto de visualización (vectores b→ → n{displaystyle {vec {B}_{n} i v→ → n{displaystyle {vec}_{n}}) multiplicado por el tamaño del píxel. A continuación presentamos fórmulas que incluyen distancia d{displaystyle d} entre el ojo y el mirador. Sin embargo, este valor se reducirá durante la normalización de los rayos r→ → ij{displaystyle {vec}_{ij}} (así que podría aceptar que d=1{displaystyle d=1} y eliminarlo de los cálculos).

Pre-calculaciones: vamos a encontrar y normalizar vector t→ → {displaystyle {vec}} vectores b→ → ,v→ → {displaystyle {vec {}},{vec {}} que son paralelos al mirador (todos representados en la imagen anterior)

t→ → =T− − E,b→ → =t→ → × × v→ → {displaystyle {vec {}=T-E,qquad {vec} {b}={vec} { t}times {vec}

t→ → n=t→ → SilencioSilenciot→ → SilencioSilencio,b→ → n=b→ → SilencioSilenciob→ → SilencioSilencio,v→ → n=t→ → n× × b→ → n{displaystyle {vec {} {fn}={fn} {fnK}{f} {fnMicrosoft} {fnMicrosoft}} {fnh}} {fn}} {fn}}}} {fn}} {fnfn}}}} {fn}}} {fnf}}}}} {fn\fnfnfnfnh}}}}}}}}}}}}}}}}}}}fnfnfn\fnfnfnfnh}}}}}}\fnfn\fnfnfnfnfnh}}}}}}}}}}}}fn\fnfn\fn\\fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnh}}}}}}} { t}tuvo la vida}}qquad {vec} {b}_{n}={frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft Sans Serif} {fn}} {fnMicrosoft}} {fnh} {fn}} {fnMicrosoft} {fnMicrosoft}} {f}}}f}}}}} {f}}f}}}}}}f}}}}fnh}}f}f}f}f}f}}f}fnhf}fnhfnhfnh}fnhfnh}}fnhfnhfnh}fnhfnh}fnfnhfnhfnhfnhfnh}fnh}fnhfnh}fnfnh}fnhfnh}fnh {b} sobrevivir}}qquad {fn} {fn}={vec} {}_{n}times {vec} {b}_{n}

nota que mirador centro C=E+t→ → nd{displaystyle C=E+{vec {}_} {}d}, siguiente calculamos los tamaños de los miradores hx,hSí.{displaystyle ¿Qué? dividido por 2 incluyendo la relación de aspecto inverso m− − 1k− − 1{fnMicroc} {m-1}{k-1}}

gx=hx2=d#⁡ ⁡ Silencio Silencio 2,gSí.=hSí.2=gxm− − 1k− − 1{displaystyle G_{x}={frac {h_{x}{2}=dtan {fnMicroc {theta} }{2},qquad g_{y}={frac {fnK} {fnK}}=g_{x}{frac} {f} {fnK} {f}} {f} {fn}} {f}} {fn}}}} {fn}}} {f} {f}} {f}}} {f}}}}}} {f}}}} {f}}}}}}}}}}} {g_g_g_g_g_g_g_g_g} {f} {f} {f} {f} {f}} {f} {f} {f} {f}}}}}}}} {f} {f} {f}} {f}} {f}} {f}}}}}}}f} {f} {f} {f} {f}f}}}}}}}}}}}}}}} {f}}}}}} {m-1}{k-1}}

y luego calculamos vectores de cambio de píxeles qx,qSí.{displaystyle q_{x},q_{y} a lo largo de las direcciones paralelas al televideo (b→ → ,v→ → {displaystyle {vec {}},{vec {}}), y el centro de pixel inferior izquierdo p1m{displaystyle P_{1m}

q→ → x=2gxk− − 1b→ → n,q→ → Sí.=2gSí.m− − 1v→ → n,p→ → 1m=t→ → nd− − gxb→ → n− − gSí.v→ → n{displaystyle {vec {q}_{x}={frac} {2g_{x}{k-1}{vec {b}_{n},qquad {vec {q}_{y}={frac} {2g_{y}{m-1}{vec {}_{n},qquad {vec} {p}_{1m}={vec} {} {fn}d-g_{x}{vec} {fn} {fn} {fn} {fn} {fn} {fn} {fn}} {fn}} {fn} {fn}} {fn}} {fn} {fn}}} {fn}} {fn}}}}}}} {fn}}}} {f} {g}}} {g}}}}}}} {g}}}}} {g}}}}}} {g}}}}} {g} {g} {g}}}} {g}}}}}}}}}} {g}}}}}}}} {g} {g}}}}}}}} {g}}} {g} {g} {g} {g}}}}}} {g}}}}}}} {g}}}}}}}}}}}}}}}}}}}}} {fn}

Cálculos: nota Pij=E+p→ → ij{displaystyle P_{ij}=E+{vec {p}_{ij} y rayos R→ → ij=Pij− − E=p→ → ij{displaystyle {vec {R}_{ij}=P_{ij}-E={vec} {p}_{ij} Así que...

p→ → ij=p→ → 1m+q→ → x()i− − 1)+q→ → Sí.()j− − 1){displaystyle {vec {p}_{y}={vec} [p}_{1m}+{vec}_{x}(i-1)+{vec {q}_{y}(j-1)}

r→ → ij=R→ → ijSilencioSilencioR→ → ijSilencioSilencio=p→ → ijSilencioSilenciop→ → ijSilencioSilencio{displaystyle {vec {fnK} {fnMicroc} {fnMic {fnh} {fnh} {fnMicrosoft} {fnh}} {fnh}} {fn}} {fn}}} {fn}}} {fn}}} {fn}}}} {\fnh}} {f}}}} {fnf}}}} {f}}}}}}}}}}} {\f}}}}}}}}}}\\\fnf}}}}}}}}}\f}}}}\fn\\fn\fn\\\f}}}}}fn\fnfnfnfn\\fn\\fnfnfnfnfnfnfnh}fnfnh}}\fn\\fnh}}}}}fn {R}_{ij} sobrevivir {fnMic {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {f}} {fn}} {f}} {fn}}} {fnMicrosoft}}} {fnh}}}}} {f}}} {f}}}}}} {fnf}}}} {f}}}} {\f}}}}}}}}}}}} {\f}}}}f}}}}}}}}}}}}f}}}}}} {\\f}}}}}}f}}f}}}} {\f}}}}}}}}}}}}}}} {f}}} {\f}f}}fn\fnf}f}}}}}}fn\fnh}f}}fn\f}f}}}}}}}}}}} {fnK} {fnK}} {fnK}}}} {fn}}} {fn}}}}} {f}} {fn}}}} {fn}}}}} {fn}}}}}

La fórmula anterior se probó en este proyecto de JavaScript (funciona en el navegador).

Descripción detallada del algoritmo informático de trazado de rayos y su génesis

Lo que sucede en la naturaleza (simplificado)

En la naturaleza, una fuente de luz emite un rayo de luz que viaja, eventualmente, a una superficie que interrumpe su avance. Uno puede pensar en este "rayo" como una corriente de fotones que viajan a lo largo del mismo camino. En un vacío perfecto, este rayo será una línea recta (ignorando los efectos relativistas). Cualquier combinación de cuatro cosas podría ocurrir con este rayo de luz: absorción, reflexión, refracción y fluorescencia. Una superficie puede absorber parte del rayo de luz, dando como resultado una pérdida de intensidad de la luz reflejada y/o refractada. También puede reflejar todo o parte del rayo de luz, en una o más direcciones. Si la superficie tiene propiedades transparentes o translúcidas, refracta una parte del haz de luz hacia sí mismo en una dirección diferente mientras absorbe parte (o todo) del espectro (y posiblemente altera el color). Con menos frecuencia, una superficie puede absorber una parte de la luz y volver a emitir la luz de forma fluorescente en un color de longitud de onda más larga en una dirección aleatoria, aunque esto es tan raro que se puede descartar de la mayoría de las aplicaciones de renderizado. Entre la absorción, la reflexión, la refracción y la fluorescencia, se debe tener en cuenta toda la luz entrante, y nada más. Una superficie no puede, por ejemplo, reflejar el 66 % de un rayo de luz entrante y refractar el 50 %, ya que los dos suman el 116 %. A partir de aquí, los rayos reflejados y/o refractados pueden incidir en otras superficies, donde sus propiedades de absorción, refracción, reflexión y fluorescencia afectan de nuevo al progreso de los rayos entrantes. Algunos de estos rayos viajan de tal manera que golpean nuestros ojos, lo que nos hace ver la escena y así contribuir a la imagen renderizada final.

Algoritmo de emisión de rayos

La idea detrás de la proyección de rayos, el predecesor del trazado de rayos recursivo, es rastrear rayos desde el ojo, uno por píxel, y encontrar el objeto más cercano que bloquea el camino de ese rayo. Piense en una imagen como una puerta de pantalla, en la que cada cuadrado de la pantalla es un píxel. Este es entonces el objeto que el ojo ve a través de ese píxel. Usando las propiedades del material y el efecto de las luces en la escena, este algoritmo puede determinar el sombreado de este objeto. Se hace la suposición simplificadora de que si una superficie se enfrenta a una luz, la luz alcanzará esa superficie y no quedará bloqueada ni en la sombra. El sombreado de la superficie se calcula utilizando modelos tradicionales de sombreado de gráficos por computadora en 3D. Una ventaja importante de la proyección de rayos que se ofrecía sobre los algoritmos de línea de exploración más antiguos era su capacidad para manejar fácilmente superficies y sólidos no planos, como conos y esferas. Si una superficie matemática puede intersecarse con un rayo, se puede renderizar utilizando la proyección de rayos. Se pueden crear objetos elaborados utilizando técnicas de modelado sólido y se pueden renderizar fácilmente.

Algoritmo de emisión de rayos de volumen

En el método de emisión de rayos de volumen, cada rayo se rastrea para que el color y/o la densidad puedan muestrearse a lo largo del rayo y luego combinarse en un color de píxel final. Esto se usa a menudo cuando los objetos no se pueden representar fácilmente mediante superficies explícitas (como triángulos), por ejemplo, al renderizar nubes o escaneos médicos en 3D.

Visualización del algoritmo de marcha de rayos SDF

Algoritmo de marcha de rayos SDF

En la marcha de rayos SDF, o trazado de esferas, cada rayo se rastrea en varios pasos para aproximar un punto de intersección entre el rayo y una superficie definida por una función de distancia con signo (SDF). El SDF se evalúa para cada iteración para poder dar pasos tan grandes como sea posible sin perder ninguna parte de la superficie. Se utiliza un umbral para cancelar más iteraciones cuando se alcanza un punto que está lo suficientemente cerca de la superficie. Este método se utiliza a menudo para la representación de fractales en 3D.

Algoritmo de trazado de rayos recursivo

El rastreo de Ray puede crear imágenes fotorrealistas.

Además del alto grado de realismo, el rastreo de rayos puede simular los efectos de una cámara debido a la profundidad del campo y la forma de abertura (en este caso un hexágono).

El número de reflexiones, o rebotes, un “ray” puede hacer, y cómo se afecta cada vez que se encuentra con una superficie, es controlado por la configuración del software. En esta imagen, se permitió que cada rayo reflejara hasta 16 veces. En estas esferas se pueden observar múltiples “reflexiones de reflexiones”. (Imagen creada con Cobalt.)

El número de refracciones puede hacer un “ray” y cómo se afecta cada vez que se encuentra con una superficie que permite la transmisión de la luz, se controla por configuraciones en el software. Aquí, cada rayo fue establecido para refractar o reflejar (el "de profundidad") hasta 9 veces. Se utilizaron reflejos de fresnel y los caustics son visibles. (Imagen creada con V-Ray.)

Los algoritmos anteriores rastreaban rayos desde el ojo hasta la escena hasta que golpeaban un objeto, pero determinaban el color del rayo sin rastrear recursivamente más rayos. El trazado de rayos recursivo continúa el proceso. Cuando un rayo golpea una superficie, se pueden emitir rayos adicionales debido a la reflexión, la refracción y la sombra.:

• Un rayo de reflexión se rastrea en la dirección de reflexión del espejo. El objeto más cercano que intersecte es lo que se verá en la reflexión.
• Un rayo de refracción que viaja a través de materiales transparentes funciona de manera similar, con la adición de que un rayo refractivo podría entrar o salir de un material. Turner Whitted extendió la lógica matemática para los rayos pasando a través de un sólido transparente para incluir los efectos de la refracción.
• Un rayo de sombra se rastrea hacia cada luz. Si se encuentra algún objeto opaco entre la superficie y la luz, la superficie está en la sombra y la luz no la ilumina.

Estos rayos recursivos añaden más realismo a las imágenes con trazado de rayos.

Ventajas sobre otros métodos de renderizado

La popularidad del renderizado basado en el trazado de rayos proviene de su base en una simulación realista del transporte ligero, en comparación con otros métodos de renderizado, como la rasterización, que se centra más en la simulación realista de la geometría. Los efectos como los reflejos y las sombras, que son difíciles de simular con otros algoritmos, son un resultado natural del algoritmo de trazado de rayos. La independencia computacional de cada rayo hace que el trazado de rayos sea compatible con un nivel básico de paralelización, pero la divergencia de las trayectorias de los rayos hace que la alta utilización bajo paralelismo sea bastante difícil de lograr en la práctica.

Desventajas

Una gran desventaja del trazado de rayos es el rendimiento (aunque, en teoría, puede ser más rápido que el renderizado de línea de exploración tradicional según la complejidad de la escena frente al número de píxeles en pantalla). Hasta finales de la década de 2010, el trazado de rayos en tiempo real generalmente se consideraba imposible en el hardware de consumo para tareas no triviales. Los algoritmos de línea de exploración y otros algoritmos utilizan la coherencia de datos para compartir cálculos entre píxeles, mientras que el trazado de rayos normalmente inicia el proceso de nuevo, tratando cada rayo del ojo por separado. Sin embargo, esta separación ofrece otras ventajas, como la capacidad de disparar más rayos según sea necesario para realizar suavizado espacial y mejorar la calidad de la imagen donde sea necesario.

Aunque maneja con precisión la interreflexión y los efectos ópticos como la refracción, el trazado de rayos tradicional tampoco es necesariamente fotorrealista. El verdadero fotorrealismo ocurre cuando la ecuación de renderizado se aproxima mucho o se implementa por completo. La implementación de la ecuación de renderizado brinda verdadero fotorrealismo, ya que la ecuación describe todos los efectos físicos del flujo de luz. Sin embargo, esto suele ser inviable debido a los recursos informáticos necesarios.

El realismo de todos los métodos de renderizado se puede evaluar como una aproximación a la ecuación. El trazado de rayos, si se limita al algoritmo de Whitted, no es necesariamente el más realista. Los métodos que rastrean los rayos, pero incluyen técnicas adicionales (mapeo de fotones, rastreo de caminos), brindan una simulación mucho más precisa de la iluminación del mundo real.

Dirección invertida de recorrido de la escena por los rayos

El proceso de disparar rayos desde el ojo a la fuente de luz para generar una imagen a veces se denomina trazado de rayos hacia atrás, ya que es la dirección opuesta en la que viajan los fotones. Sin embargo, existe confusión con esta terminología. El primer trazado de rayos siempre se hacía desde el ojo, y los primeros investigadores, como James Arvo, usaban el término trazado de rayos hacia atrás para referirse a disparar rayos desde las luces y recopilar los resultados. Por lo tanto, es más claro distinguir entre el trazado de rayos basado en el ojo y el trazado de rayos basado en la luz.

Si bien la iluminación directa generalmente se muestrea mejor mediante el trazado de rayos basado en el ojo, ciertos efectos indirectos pueden beneficiarse de los rayos generados por las luces. Los cáusticos son patrones brillantes causados por el enfoque de la luz de una amplia región reflectante en un área estrecha de superficie (casi) difusa. Un algoritmo que emita rayos directamente desde las luces sobre objetos reflectantes, siguiendo sus caminos hasta el ojo, muestreará mejor este fenómeno. Esta integración de rayos basados en el ojo y en la luz se expresa a menudo como un trazado de trayectoria bidireccional, en el que las trayectorias se trazan tanto desde el ojo como desde las luces, y las trayectorias se unen posteriormente mediante un rayo de conexión después de cierta longitud.

El mapeo de fotones es otro método que utiliza tanto el trazado de rayos basado en la luz como en el ojo; en un paso inicial, los fotones energéticos se rastrean a lo largo de los rayos de la fuente de luz para calcular una estimación del flujo radiante en función del espacio tridimensional (el mapa de fotones del mismo nombre). En una pasada posterior, los rayos se trazan desde el ojo hasta la escena para determinar las superficies visibles y el mapa de fotones se utiliza para estimar la iluminación en los puntos de la superficie visible. La ventaja del mapeo de fotones frente al rastreo de rutas bidireccional es la capacidad de lograr una reutilización significativa de fotones, lo que reduce la computación, a costa del sesgo estadístico.

Ocurre un problema adicional cuando la luz debe pasar a través de una abertura muy estrecha para iluminar la escena (considere una habitación oscura, con una puerta entreabierta que conduce a una habitación muy iluminada), o una escena en la que la mayoría de los puntos no tienen luz directa. línea de visión a cualquier fuente de luz (como con artefactos de iluminación o antorchas dirigidas al techo). En tales casos, solo un subconjunto muy pequeño de caminos transportará energía; El transporte ligero de Metropolis es un método que comienza con una búsqueda aleatoria del espacio del camino, y cuando se encuentran caminos energéticos, reutiliza esta información explorando el espacio cercano de los rayos.

Imagen que muestra rayos generados recursivamente desde el "ojo" (y a través de un plano de imagen) a una fuente de luz después de encontrar dos superficies difusas

A la derecha hay una imagen que muestra un ejemplo simple de una ruta de rayos generados recursivamente desde la cámara (o el ojo) hasta la fuente de luz usando el algoritmo anterior. Una superficie difusa refleja la luz en todas las direcciones.

Primero, se crea un rayo en un punto de vista y se traza a través de un píxel hasta la escena, donde golpea una superficie difusa. A partir de esa superficie, el algoritmo genera recursivamente un rayo de reflexión, que se traza a través de la escena, donde golpea otra superficie difusa. Finalmente, se genera otro rayo de reflexión y se traza a través de la escena, donde golpea la fuente de luz y es absorbido. El color del píxel ahora depende de los colores de la primera y segunda superficie difusa y del color de la luz emitida por la fuente de luz. Por ejemplo, si la fuente de luz emite luz blanca y las dos superficies difusas son azules, el color resultante del píxel es azul.

Ejemplo

Como demostración de los principios involucrados en el trazado de rayos, considere cómo se encontraría la intersección entre un rayo y una esfera. Esta es simplemente la matemática detrás de la intersección línea-esfera y la posterior determinación del color del píxel que se calcula. Por supuesto, hay mucho más en el proceso general de trazado de rayos, pero esto demuestra un ejemplo de los algoritmos utilizados.

En la notación vectorial, la ecuación de una esfera con centro c{displaystyle mathbf {c} y radio r{displaystyle r} es

.x− − c.2=r2.{displaystyle left Vert mathbf {x} -mathbf {c} right Vert ^{2}=r^{2}

Cualquier punto en un rayo desde el punto s{displaystyle mathbf {s} con dirección d{displaystyle mathbf {d} (Aquí) d{displaystyle mathbf {d} es un vector de unidad) se puede escribir como

x=s+td,{displaystyle mathbf {x} = 'mathbf {s} - No.

Donde t{displaystyle t} es su distancia entre x{displaystyle mathbf {x} y s{displaystyle mathbf {s}. En nuestro problema, sabemos c{displaystyle mathbf {c}, r{displaystyle r}, s{displaystyle mathbf {s} (por ejemplo, la posición de una fuente de luz) y d{displaystyle mathbf {d}, y necesitamos encontrar t{displaystyle t}. Por lo tanto, sustituimos para x{displaystyle mathbf {x}:

.s+td− − c.2=r2.{displaystyle left Vert mathbf {s} +tmathbf {d} - Mathbf {c} right Vert ^{2}=r^{2}

Vamos v=defs− − c{displaystyle mathbf {v} {f} {f} {f} {f} {f}} {f}} {f}}}}}\f}}}\f}}\\fn}\\\f}\f}}}}\\fn}}}}\\ {} - Mathbf {c} para la simplicidad; entonces

.v+td.2=r2{displaystyle left Vert mathbf {v} +tmathbf {d} right Vert ^{2}=r^{2}

v2+t2d2+2v⋅ ⋅ td=r2{displaystyle mathbf {v} ^{2}+t^{2}mathbf {d} ^{2}+2mathbf {v}cdot tmathbf {d} =r^{2}}

()d2)t2+()2v⋅ ⋅ d)t+()v2− − r2)=0.{displaystyle (mathbf {d} ^{2})t^{2}+(2mathbf {v} cdot mathbf {d})t+(mathbf {v} ^{2}-r^{2})=0. }

Saber que d es un vector unitario nos permite esta pequeña simplificación:

t2+()2v⋅ ⋅ d)t+()v2− − r2)=0.{displaystyle t^{2}+(2mathbf {v} cdot mathbf {d})t+(mathbf {v} ^{2}-r^{2})=0. }

Esta ecuación cuadrática tiene soluciones

t=− − ()2v⋅ ⋅ d)± ± ()2v⋅ ⋅ d)2− − 4()v2− − r2)2=− − ()v⋅ ⋅ d)± ± ()v⋅ ⋅ d)2− − ()v2− − r2).{f} {f} {f} {f} {f}} {f} {f}} {f} {f}} {f} {f}} {f} {f} {f}} {f}} {f}} {f} {b} {f}ccH0}}}} {c}} {b} {f}c} {ccc}ccc}ccc}c}cccccccccccccccccccccccccccccccccccccccc}cccccccccc}ccccccc}c}c

Los dos valores de t{displaystyle t} encontrado por la resolución de esta ecuación son los dos tal que s+td{displaystyle mathbf {s} +tmathbf {d} son los puntos donde el rayo intersecte la esfera.

Cualquier valor negativo no miente en el rayo, sino más bien en la media línea opuesta (es decir, el que comienza desde s{displaystyle mathbf {s} con dirección opuesta).

Si la cantidad debajo de la raíz cuadrada (el discriminante) es negativa, entonces el rayo no corta la esfera.

Supongamos ahora que hay al menos una solución positiva, y dejemos t{displaystyle t} Sé el mínimo. Además, supongamos que la esfera es el objeto más cercano en nuestra escena que intersecte nuestro rayo, y que está hecha de un material reflectante. Necesitamos encontrar en qué dirección se refleja el rayo de luz. Las leyes de reflexión declaran que el ángulo de reflexión es igual y opuesto al ángulo de incidencia entre el rayo incidente y lo normal en la esfera.

La normal a la esfera es simplemente

n=Sí.− − c.Sí.− − c.,{displaystyle mathbf {n} ={frac {mathbf {y} - Mathbf {c} }{left Vert mathbf {y} -mathbf {c} right ¿Vert?

Donde Sí.=s+td{displaystyle mathbf {y} =mathbf {s} - No. es el punto de intersección encontrado antes. La dirección de reflexión se puede encontrar por un reflejo de d{displaystyle mathbf {d} con respecto a n{displaystyle mathbf {n}, eso es

r=d− − 2()n⋅ ⋅ d)n.{displaystyle mathbf {r} =mathbf {d} -2(mathbf {n} cdot mathbf {d})mathbf {n}.

Así, el rayo reflejado tiene ecuación

x=Sí.+ur.{displaystyle mathbf {x} # Mathbf # - No.

Ahora solo necesitamos calcular la intersección del último rayo con nuestro campo de visión, para obtener el píxel en el que incidirá nuestro rayo de luz reflejado. Por último, este píxel se establece en un color apropiado, teniendo en cuenta cómo el color de la fuente de luz original y el de la esfera se combinan por el reflejo.

Control de profundidad adaptable

El control de profundidad adaptativo significa que el renderizador deja de generar rayos reflejados/transmitidos cuando la intensidad calculada es inferior a cierto umbral. Siempre debe haber una profundidad máxima establecida o de lo contrario el programa generaría un número infinito de rayos. Pero no siempre es necesario llegar a la máxima profundidad si las superficies no son muy reflectantes. Para probar esto, el trazador de rayos debe calcular y mantener el producto de los coeficientes global y de reflexión a medida que se trazan los rayos.

Ejemplo: sea Kr = 0,5 para un conjunto de superficies. Entonces de la primera superficie la contribución máxima es 0.5, para la reflexión de la segunda: 0.5 × 0.5 = 0.25, la tercera: 0.25 × 0.5 = 0.125, la cuarta: 0.125 × 0.5 = 0.0625, la quinta: 0.0625 × 0.5 = 0.03125, etc. Además, podríamos implementar un factor de atenuación de distancia como 1/D2, que también disminuiría la contribución de intensidad.

Para un rayo transmitido, podríamos hacer algo similar, pero en ese caso, la distancia recorrida a través del objeto provocaría una disminución de la intensidad aún más rápida. Como ejemplo de esto, Hall & Greenberg encontró que incluso para una escena muy reflexiva, usar esto con una profundidad máxima de 15 dio como resultado una profundidad de árbol de rayos promedio de 1.7.

Volúmenes delimitadores

Encerrar grupos de objetos en conjuntos de volúmenes delimitadores jerárquicos reduce la cantidad de cálculos necesarios para el trazado de rayos. Primero se prueba un rayo proyectado para una intersección con el volumen delimitador, y luego, si hay una intersección, el volumen se divide recursivamente hasta que el rayo golpea el objeto. El mejor tipo de volumen delimitador estará determinado por la forma del objeto u objetos subyacentes. Por ejemplo, si los objetos son largos y delgados, una esfera encerrará principalmente un espacio vacío en comparación con una caja. Las cajas también son más fáciles de generar volúmenes delimitadores jerárquicos.

Tenga en cuenta que el uso de un sistema jerárquico como este (suponiendo que se haga con cuidado) cambia el tiempo de cálculo de la intersección de una dependencia lineal del número de objetos a algo entre una dependencia lineal y logarítmica. Esto se debe a que, para un caso perfecto, cada prueba de intersección dividiría las posibilidades por dos y daría como resultado una estructura de tipo árbol binario. Los métodos de subdivisión espacial, discutidos a continuación, intentan lograr esto.

Kay & Kajiya proporciona una lista de propiedades deseadas para volúmenes delimitadores jerárquicos:

• Los subárboles deben contener objetos que están cerca uno del otro y el otro más abajo del árbol el más cerca debe ser los objetos.
• El volumen de cada nodo debe ser mínimo.
• La suma de los volúmenes de todos los volúmenes consolidados debe ser mínima.
• Debe prestarse mayor atención a los nodos cerca de la raíz ya que la poda de una rama cerca de la raíz eliminará más objetos potenciales que uno más allá del árbol.
• El tiempo dedicado a construir la jerarquía debe ser mucho menos que el tiempo ahorrado por utilizarla.

Trazado de rayos interactivo

La primera implementación de un trazador de rayos interactivo fue el sistema de gráficos por computadora LINKS-1 construido en 1982 en la Escuela de Ingeniería de la Universidad de Osaka por los profesores Ohmura Kouichi, Shirakawa Isao y Kawata Toru con 50 estudiantes. Era un sistema informático de procesamiento masivo en paralelo con 514 microprocesadores (257 Zilog Z8001 y 257 iAPX 86), que se utilizaba para generar gráficos 3D realistas por computadora con trazado de rayos de alta velocidad. Según la Sociedad de Procesamiento de la Información de Japón: "El núcleo de la representación de imágenes 3D es calcular la luminancia de cada píxel que forma una superficie renderizada desde el punto de vista, la fuente de luz y la posición del objeto dados. El sistema LINKS-1 se desarrolló para realizar una metodología de representación de imágenes en la que cada píxel podría procesarse en paralelo de forma independiente mediante el trazado de rayos. Mediante el desarrollo de una nueva metodología de software específicamente para la representación de imágenes de alta velocidad, LINKS-1 pudo generar rápidamente imágenes muy realistas." Se usó para crear un video de los cielos similar a un planetario en 3D hecho completamente con gráficos de computadora. El video fue presentado en el pabellón de Fujitsu en la Exposición Internacional de 1985 en Tsukuba." Fue el segundo sistema en hacerlo después de Evans & Sutherland Digistar en 1982. Se informó que LINKS-1 era la computadora más poderosa del mundo en 1984.

El registro público más antiguo de "en tiempo real" El trazado de rayos con renderizado interactivo (es decir, actualizaciones de más de un cuadro por segundo) fue acreditado en la conferencia de gráficos por computadora SIGGRAPH de 2005 como las herramientas REMRT/RT desarrolladas en 1986 por Mike Muuss para el sistema de modelado sólido BRL-CAD. Publicado inicialmente en 1987 en USENIX, el trazador de rayos BRL-CAD fue una implementación temprana de un sistema de trazado de rayos distribuido en red paralela que logró varios fotogramas por segundo en el rendimiento de representación. Este rendimiento se logró mediante el motor de trazado de rayos LIBRT altamente optimizado pero independiente de la plataforma en BRL-CAD y mediante el uso de geometría CSG implícita sólida en varias máquinas paralelas de memoria compartida en una red de productos básicos. El trazador de rayos de BRL-CAD, incluidas las herramientas REMRT/RT, siguen estando disponibles y se desarrollan actualmente como software de código abierto.

Desde entonces, se han realizado considerables esfuerzos e investigaciones para implementar el trazado de rayos a velocidades en tiempo real para una variedad de propósitos en configuraciones de escritorio independientes. Estos propósitos incluyen aplicaciones gráficas 3D interactivas, como producciones de demostración, juegos de computadora y de video, y representación de imágenes. Algunos motores 3D de software en tiempo real basados en trazado de rayos han sido desarrollados por programadores de demostración aficionados desde finales de la década de 1990.

En 1999, un equipo de la Universidad de Utah, dirigido por Steven Parker, hizo una demostración en directo del trazado de rayos interactivo en el Simposio de gráficos 3D interactivos de 1999. Procesaron un modelo de 35 millones de esferas con una resolución de 512 x 512 píxeles, funcionando a aproximadamente 15 fotogramas por segundo en 60 CPU.

El proyecto Open RT incluía un núcleo de software altamente optimizado para el trazado de rayos junto con una API similar a OpenGL para ofrecer una alternativa al enfoque actual basado en rasterización para gráficos 3D interactivos. El hardware de trazado de rayos, como la Unidad de procesamiento de rayos experimental desarrollada por Sven Woop en la Universidad de Saarland, ha sido diseñado para acelerar algunas de las operaciones computacionalmente intensivas del trazado de rayos.

La idea de que los videojuegos pudieran trazar sus gráficos con ray tracing en tiempo real recibió la atención de los medios a fines de la década de 2000. Durante ese tiempo, un investigador llamado Daniel Pohl, bajo la dirección del profesor de gráficos Philipp Slusallek y en cooperación con la Universidad de Erlangen y la Universidad de Saarland en Alemania, equipó Quake III y Quake IV con un motor que él mismo programó, que luego la Universidad de Saarland demostró en CeBIT 2007. Intel, patrocinador de Saarland, quedó tan impresionado que contrató a Pohl y se embarcó en un programa de investigación dedicado a los gráficos con trazado de rayos, que consideró que justificaba aumentar el número de sus procesadores' núcleos El 12 de junio de 2008, Intel hizo una demostración de una versión especial de Enemy Territory: Quake Wars, titulada Quake Wars: Ray Traced, utilizando el trazado de rayos para el renderizado, ejecutándose en HD básico (720p) de resolución. ETQW funcionaba a entre 14 y 29 fotogramas por segundo en un sistema Xeon Tigerton de 16 núcleos (4 zócalos, 4 núcleos) que funcionaba a 2,93 GHz.

En SIGGRAPH 2009, Nvidia anunció OptiX, una API gratuita para el trazado de rayos en tiempo real en las GPU de Nvidia. La API expone siete puntos de entrada programables dentro de la tubería de trazado de rayos, lo que permite cámaras personalizadas, intersecciones de rayos primitivos, sombreadores, sombras, etc. recursión de cola. Los renderizadores basados en OptiX se utilizan en Autodesk Arnold, Adobe AfterEffects, Bunkspeed Shot, Autodesk Maya, 3ds max y muchos otros renderizadores.

En 2014, una demostración del videojuego de PlayStation 4 The Tomorrow Children, desarrollado por Q-Games y Japan Studio, demostró nuevas técnicas de iluminación desarrolladas por Q-Games, en particular, el trazado de rayos de cono de vóxel en cascada., que simula la iluminación en tiempo real y utiliza reflejos más realistas en lugar de reflejos del espacio de la pantalla.

Nvidia presentó sus GPU GeForce RTX y Quadro RTX en septiembre de 2018, basadas en la arquitectura Turing que permite el trazado de rayos acelerado por hardware. El hardware de Nvidia utiliza un bloque funcional separado, llamado públicamente 'núcleo RT'. Esta unidad es algo comparable a una unidad de textura en tamaño, latencia e interfaz con el núcleo del procesador. La unidad cuenta con BVH transversal, descompresión de nodo BVH comprimido, prueba de intersección de rayos-AABB y prueba de intersección de rayos-triángulo. La GeForce RTX, en forma de modelos 2080 y 2080 Ti, se convirtió en la primera marca de tarjeta gráfica orientada al consumidor que puede procesar el trazado de rayos en tiempo real y, en noviembre de 2018, Electronic Arts' Battlefield V se convirtió en el primer juego en aprovechar sus capacidades de trazado de rayos, que logra a través de la nueva API de Microsoft, DirectX Raytracing. AMD, que ya ofrecía trazado de rayos interactivo además de OpenCL a través de Radeon ProRender, presentó en octubre de 2020 la serie Radeon RX 6000, sus GPU Navi de segunda generación con soporte para trazado de rayos acelerado por hardware en un evento en línea. Desde entonces, aparecieron juegos posteriores que representan sus gráficos por tales medios, lo que se atribuye a las mejoras en el hardware y los esfuerzos para hacer que más API y motores de juegos sean compatibles con la tecnología. Las consolas de juegos domésticas actuales implementan componentes de hardware de trazado de rayos dedicados en sus GPU para efectos de trazado de rayos en tiempo real, que comenzaron con las consolas de novena generación PlayStation 5, Xbox Series X y Series S.

Complejidad computacional

Se han probado varios resultados de complejidad para ciertas formulaciones del problema de trazado de rayos. En particular, si la versión de decisión del problema de trazado de rayos se define de la siguiente manera: dada la posición y dirección inicial de un rayo de luz y algún punto fijo, ¿el rayo finalmente llega a ese punto? Entonces, el artículo al que se hace referencia demuestra los siguientes resultados.:

• El rastreo de rayos en sistemas ópticos 3D con un conjunto finito de objetos reflectantes o refractivos representados por un sistema de desigualdades cuadráticas racionales es indecible.
• El rastreo de rayos en sistemas ópticos 3D con un conjunto finito de objetos refractivos representados por un sistema de desigualdades lineales racionales es indecible.
• El trazado de rayos en sistemas ópticos 3D con un conjunto finito de objetos reflectantes o refractivos rectangulares es indecible.
• El rastreo de rayos en sistemas ópticos 3D con un conjunto finito de objetos reflectantes o parcialmente reflexivos representado por un sistema de desigualdades lineales, algunos de los cuales pueden ser irracionales es indecible.
• El rastreo de rayos en sistemas ópticos 3D con un conjunto finito de objetos reflectantes o parcialmente reflexivos representado por un sistema de desigualdades lineales racionales es difícil de PSPACE.
• Para cualquier dimensión igual o superior a 2, el rastreo de rayos con un conjunto finito de superficies reflectantes paralelas y perpendiculares representadas por desigualdades lineales racionales está en PSPACE.