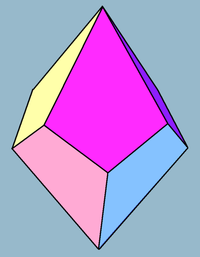
Trapezoedro tetragonal
| Tetragonal trapezohedron | |
|---|---|
 Haga clic en la imagen para la versión grande. | |
| Tipo | trapezohedra |
| Conway | dA4 |
| Coxeter diagrama |      |
| Caras | 8 cometas |
| Edges | 16 |
| Vertices | 10 |
| Configuración facial | V4.3.3.3 |
| Grupo de simetría | D4d[2]+,8], (2*4), orden 16 |
| Grupo de rotación | D4[2,4]+, (224), orden 8 |
| Poliedro dual | Antiprisma cuadrado |
| Propiedades | convex, face-transitive |
En geometría, un trapezoedro tetragonal, o deltoedro, es el segundo de una serie infinita de trapezoedros, que son duales a los antiprismas. Tiene ocho caras, que son cometas congruentes, y es dual al antiprisma cuadrado.
En generación de malla
Esta forma se ha utilizado como caso de prueba para la generación de mallas hexaédricas, simplificando un caso de prueba anterior propuesto por el matemático Robert Schneiders en forma de pirámide cuadrada con su límite subdividido en 16 cuadriláteros. En este contexto, al trapezoedro tetragonal también se le ha llamado octaedro cúbico, octaedro cuadrilátero o huso octogonal, porque tiene ocho caras cuadriláteras y es definido únicamente como un poliedro combinatorio por esa propiedad. Agregar cuatro cuboides a una malla para el octaedro cúbico también daría una malla para la malla de Schneiders. pirámide. Como poliedro simplemente conectado con un número par de caras cuadriláteras, el octaedro cúbico se puede descomponer en cuboides topológicos con caras curvas que se encuentran cara a cara sin subdividir los cuadriláteros límite, y se ha construido una malla explícita de este tipo. Sin embargo, no está claro si se puede obtener una descomposición de este tipo en la que todos los cuboides sean poliedros convexos con caras planas.
En el arte
Un trapezoedro tetragonal aparece en la parte superior izquierda como una de las "estrellas" en el grabado en madera de M. C. Escher de 1948, Estrellas.
Mosaico esférico
El trapezoedro tetragonal también existe como un mosaico esférico, con 2 vértices en los polos y vértices alternos igualmente espaciados por encima y por debajo del ecuador.
Poliedros relacionados
| Nombre de Trapezohedron | Digonal trapezohedron (Tetraedro) | Trigonal trapezohedron | Tetragonal trapezohedron | Pentagonal trapezohedron | Hexagonal trapezohedron | Heptagonal trapezohedron | trapezohedro Octagonal | Decagonal trapezohedron | Dodecagonal trapezohedron | ... | Apeirogonal trapezohedron |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Imagen de poliedro |  |  | |  |  |  |  |  |  | ... | |
| Imagen de revestimiento esférico |  |  |  |  |  |  |  |  |  | Imagen de azulado plano |  |
| Configuración facial | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V dieta.3.3.3 |
El trapezoedro tetragonal es el primero de una serie de poliedros y mosaicos chatos duales con configuración de cara V3.3.4.3.n.
| 4n2 mutaciones de la simetría de las baldosas del snub: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Simmetría 4n2 | Spherical | Euclidean | Hiperbólico compacto | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | JUEGO42 | |
| Snub cifras |  |  |  |  |  |  |  |  |
| Config. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3. |
| Gyro cifras | |  |  |  | ||||
| Config. | V3.3.4.3.2 | V3.3.4.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3. |