Transición de fase
En química, termodinámica y otros campos relacionados, una transición de fase (o cambio de fase) es el proceso físico de transición entre un estado de un medio y otro. Comúnmente, el término se usa para referirse a cambios entre los estados básicos de la materia: sólido, líquido y gas, y en casos raros, plasma. Una fase de un sistema termodinámico y los estados de la materia tienen propiedades físicas uniformes. Durante una transición de fase de un medio dado, ciertas propiedades del medio cambian como resultado del cambio de las condiciones externas, como la temperatura o la presión. Esto puede ser un cambio discontinuo; por ejemplo, un líquido puede convertirse en gas al calentarse hasta su punto de ebullición, lo que resulta en un cambio abrupto de volumen. La identificación de las condiciones externas en las que se produce una transformación define el punto de transición de fase.
Tipos de transición de fase
En el punto de transición de fase de una sustancia, por ejemplo, el punto de ebullición, las dos fases involucradas, líquido y vapor, tienen energías libres idénticas y, por lo tanto, es igualmente probable que existan. Por debajo del punto de ebullición, el líquido es el estado más estable de los dos, mientras que por encima del punto de ebullición, la forma gaseosa es la más estable.
A veces es posible cambiar el estado de un sistema diabáticamente (en oposición a adiabáticamente) de tal manera que pueda pasar un punto de transición de fase sin sufrir una transición de fase. El estado resultante es metaestable, es decir, menos estable que la fase a la que se habría producido la transición, pero tampoco inestable. Esto ocurre en sobrecalentamiento, sobreenfriamiento y sobresaturación, por ejemplo.
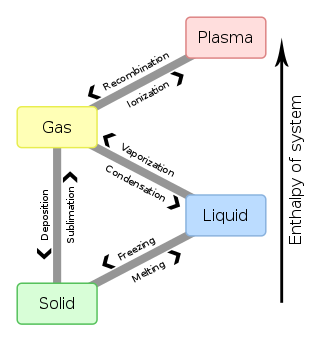
Las transiciones comunes entre las fases sólida, líquida y gaseosa de un solo componente, debido a los efectos de la temperatura y/o la presión, se identifican en la siguiente tabla:
A Desde | Sólido | Líquido | Gas | Plasma |
|---|---|---|---|---|
| Sólido | Melting | Sublimación | ||
| Líquido | Freezing | Vaporización | ||
| Gas | Deposición | Condensation | Ionización | |
| Plasma | Recombination |
Otros cambios de fase incluyen:
- Una transformación eutectica, en la que se enfría un líquido monofásico de dos componentes y se transforma en dos fases sólidas. El mismo proceso, pero comenzando con un sólido en lugar de un líquido se llama una transformación eutacoides.
- Una transformación en fase de equilibrio. Un polimorfo metastable que se forma rápidamente debido a la energía superficial inferior se transformará en una fase de equilibrio dada suficiente entrada térmica para superar una barrera energética.
- Una transformación peritectica, en la que se calienta un sólido monofásico de dos componentes y se transforma en una fase sólida y en una fase líquida.
- Una descomposición spinodal, en la que se enfría una sola fase y se separa en dos composiciones diferentes de esa misma fase.
- Transición a una mesofasa entre sólido y líquido, como una de las fases del "cristalado líquido".
- La transición entre las fases ferromagnéticas y paramagnéticas de los materiales magnéticos en el punto Curie.
- La transición entre estructuras magnéticas de orden diferente, proporcional o incommensurada, como en el antimonio del cercio.
- La transformación martensitica que se produce como una de las muchas transformaciones de fase en acero al carbono y representa un modelo para las transformaciones de fase displaciva.
- Cambios en la estructura cristalográfica como entre ferrite y austenita de hierro.
- Transiciones de orden-desordenadas como en alfa-titanio aluminides.
- La dependencia de la geometría de adsorción en la cobertura y la temperatura, como el hidrógeno en el hierro (110).
- El surgimiento de la superconductividad en ciertos metales y cerámica cuando se enfría debajo de una temperatura crítica.
- La transición entre diferentes estructuras moleculares (polymorfos, alotropos o poliamorfos), especialmente de sólidos, como entre una estructura amorfa y una estructura de cristal, entre dos estructuras de cristal diferentes, o entre dos estructuras amorfos.
- Condenación cuántica de líquidos bosónicos (condenación Bose-Einstein). La transición superfluida en helio líquido es un ejemplo de esto.
- La ruptura de las simetrías en las leyes de la física durante la historia temprana del universo como su temperatura se enfría.
- La fracción de isótopos ocurre durante una transición de fase, la relación de isótopos ligeros a isótopos pesados en las moléculas involucradas cambia. Cuando el vapor de agua se condensa (una fracción de equilibrio), los isótopos de agua más pesados (18O y 2H) se enriquezca en la fase líquida mientras los isótopos más ligeros (16O y 1H) tienden hacia la fase de vapor.
Las transiciones de fase ocurren cuando la energía libre termodinámica de un sistema no es analítica para alguna elección de variables termodinámicas (cf. fases). Esta condición generalmente se deriva de las interacciones de un gran número de partículas en un sistema y no aparece en sistemas que son pequeños. Las transiciones de fase pueden ocurrir para sistemas no termodinámicos, donde la temperatura no es un parámetro. Los ejemplos incluyen: transiciones de fase cuánticas, transiciones de fase dinámicas y transiciones de fase topológicas (estructurales). En este tipo de sistemas, otros parámetros toman el lugar de la temperatura. Por ejemplo, la probabilidad de conexión reemplaza la temperatura para las redes de filtración.
Clasificaciones
Clasificación Ehrenfest
Paul Ehrenfest clasificó las transiciones de fase basándose en el comportamiento de la energía libre termodinámica en función de otras variables termodinámicas. Bajo este esquema, las transiciones de fase fueron etiquetadas por la derivada más baja de la energía libre que es discontinua en la transición. Las transiciones de fase de primer orden exhiben una discontinuidad en la primera derivada de la energía libre con respecto a alguna variable termodinámica. Las diversas transiciones sólido/líquido/gas se clasifican como transiciones de primer orden porque implican un cambio discontinuo en la densidad, que es la (inversa de) la primera derivada de la energía libre con respecto a la presión. Las transiciones de fase de segundo orden son continuas en la primera derivada (el parámetro de orden, que es la primera derivada de la energía libre con respecto al campo externo, es continua a lo largo de la transición) pero muestran discontinuidad en una Segunda derivada de la energía libre. Estos incluyen la transición de fase ferromagnética en materiales como el hierro, donde la magnetización, que es la primera derivada de la energía libre con respecto a la intensidad del campo magnético aplicado, aumenta continuamente desde cero a medida que la temperatura desciende por debajo de la temperatura de Curie. La susceptibilidad magnética, la segunda derivada de la energía libre con el campo, cambia discontinuamente. Según el esquema de clasificación de Ehrenfest, en principio podría haber transiciones de fase de tercer, cuarto y orden superior.
La clasificación de Ehrenfest implícitamente permite transformaciones de fase continuas, donde cambia el carácter de enlace de un material, pero no hay discontinuidad en ningún derivado de energía libre. Un ejemplo de esto ocurre en los límites supercríticos líquido-gas.
El primer ejemplo de una transición de fase que no encajaba en la clasificación de Ehrenfest fue la solución exacta del modelo de Ising, descubierto en 1944 por Lars Onsager. El calor específico exacto difería de las aproximaciones de campo medio anteriores, que habían predicho que tiene una discontinuidad simple a la temperatura crítica. En cambio, el calor específico exacto tenía una divergencia logarítmica a la temperatura crítica. En las décadas siguientes, la clasificación Ehrenfest fue reemplazada por un esquema de clasificación simplificado que puede incorporar tales transiciones.
Clasificaciones modernas
En el esquema de clasificación moderno, las transiciones de fase se dividen en dos categorías amplias, nombradas de manera similar a las clases Ehrenfest:
Las transiciones de fase de primer orden son aquellas que implican un calor latente. Durante tal transición, un sistema absorbe o libera una cantidad fija (y típicamente grande) de energía por volumen. Durante este proceso, la temperatura del sistema permanecerá constante a medida que se agregue calor: el sistema está en un "régimen de fase mixta" en el que algunas partes del sistema han completado la transición y otras no.
Ejemplos familiares son el derretimiento del hielo o la ebullición del agua (el agua no se convierte instantáneamente en vapor, sino que forma una mezcla turbulenta de agua líquida y burbujas de vapor). Yoseph Imry y Michael Wortis demostraron que el desorden extinguido puede ampliar una transición de primer orden. Es decir, la transformación se completa en un rango finito de temperaturas, pero sobreviven fenómenos como el sobreenfriamiento y el sobrecalentamiento y se observa histéresis en los ciclos térmicos.
Las transiciones de fase de segundo orden también se denominan "transiciones de fase continuas". Se caracterizan por una susceptibilidad divergente, una longitud de correlación infinita y un decaimiento de la ley de potencia de las correlaciones cercanas a la criticidad. Ejemplos de transiciones de fase de segundo orden son la transición ferromagnética, la transición superconductora (para un superconductor de tipo I, la transición de fase es de segundo orden con un campo externo cero y para un superconductor de tipo II, la transición de fase es de segundo orden para ambos transiciones estado-estado mixto y estado mixto-estado superconductor) y la transición superfluida. En contraste con la viscosidad, la expansión térmica y la capacidad calorífica de los materiales amorfos muestran un cambio relativamente repentino en la temperatura de transición vítrea que permite una detección precisa utilizando mediciones de calorimetría diferencial de barrido. Lev Landau dio una teoría fenomenológica de las transiciones de fase de segundo orden.
Además de transiciones de fase simples y aisladas, existen líneas de transición así como puntos multicríticos, al variar parámetros externos como el campo magnético o la composición.
Varias transiciones se conocen como transiciones de fase de orden infinito. Son continuos pero no rompen simetrías. El ejemplo más famoso es la transición Kosterlitz-Thouless en el modelo XY bidimensional. Muchas transiciones de fase cuánticas, por ejemplo, en gases de electrones bidimensionales, pertenecen a esta clase.
La transición líquido-vítreo se observa en muchos polímeros y otros líquidos que se pueden sobreenfriar muy por debajo del punto de fusión de la fase cristalina. Esto es atípico en varios aspectos. No es una transición entre estados fundamentales termodinámicos: se cree ampliamente que el verdadero estado fundamental es siempre cristalino. El vidrio es un estado de desorden apagado, y su entropía, densidad, etc., dependen de la historia térmica. Por lo tanto, la transición vítrea es principalmente un fenómeno dinámico: al enfriarse un líquido, los grados de libertad internos pierden sucesivamente el equilibrio. Algunos métodos teóricos predicen una transición de fase subyacente en el límite hipotético de tiempos de relajación infinitamente largos. Ninguna evidencia experimental directa apoya la existencia de estas transiciones.
Se ha demostrado que la transición de gelificación de las partículas coloidales es una transición de fase de segundo orden en condiciones de desequilibrio.
Propiedades características
Coexistencia de fases
Se produce una transición de primer orden con desorden ampliado en un rango finito de temperaturas donde la fracción de la fase de equilibrio de baja temperatura crece de cero a uno (100 %) a medida que baja la temperatura. Esta continua variación de las fracciones coexistentes con la temperatura planteó interesantes posibilidades. Al enfriarse, algunos líquidos se vitrifican en forma de vidrio en lugar de transformarse en la fase cristalina de equilibrio. Esto sucede si la velocidad de enfriamiento es más rápida que una velocidad de enfriamiento crítica y se atribuye a que los movimientos moleculares se vuelven tan lentos que las moléculas no pueden reorganizarse en las posiciones del cristal. Esta desaceleración ocurre por debajo de una temperatura de formación de vidrio Tg, que puede depender de la presión aplicada. Si la transición de congelamiento de primer orden ocurre en un rango de temperaturas, y Tg cae dentro de este rango, entonces existe una posibilidad interesante de que la transición se detenga cuando es parcial e incompleto. La extensión de estas ideas a las transiciones magnéticas de primer orden detenidas a bajas temperaturas dio como resultado la observación de transiciones magnéticas incompletas, con dos fases magnéticas coexistiendo, hasta la temperatura más baja. Informado por primera vez en el caso de una transición ferromagnética a antiferromagnética, esta coexistencia de fase persistente ahora se ha informado a través de una variedad de transiciones magnéticas de primer orden. Estos incluyen materiales de manganita de magnetorresistencia colosal, materiales magnetocalóricos, materiales con memoria de forma magnética y otros materiales. La característica interesante de estas observaciones de Tg que cae dentro del rango de temperatura en el que ocurre la transición es que la transición magnética de primer orden está influenciada por el campo magnético, al igual que la la transición estructural está influenciada por la presión. La relativa facilidad con la que se pueden controlar los campos magnéticos, en contraste con la presión, plantea la posibilidad de que se pueda estudiar la interacción entre Tg y Tc de forma exhaustiva. La coexistencia de fases a través de transiciones magnéticas de primer orden permitirá la resolución de problemas pendientes en la comprensión de las gafas.
Puntos críticos
En cualquier sistema que contenga fases líquidas y gaseosas, existe una combinación especial de presión y temperatura, conocida como punto crítico, en el que la transición entre líquido y gas se convierte en una transición de segundo orden. Cerca del punto crítico, el fluido está lo suficientemente caliente y comprimido que la distinción entre las fases líquida y gaseosa es casi inexistente. Esto está asociado con el fenómeno de la opalescencia crítica, una apariencia lechosa del líquido debido a las fluctuaciones de densidad en todas las longitudes de onda posibles (incluidas las de la luz visible).
Simetría
Las transiciones de fase a menudo implican un proceso de ruptura de simetría. Por ejemplo, el enfriamiento de un fluido en un sólido cristalino rompe la simetría de traslación continua: cada punto en el fluido tiene las mismas propiedades, pero cada punto en un cristal no tiene las mismas propiedades (a menos que los puntos se elijan de los puntos de red de la red cristalina). Por lo general, la fase de alta temperatura contiene más simetrías que la fase de baja temperatura debido a la ruptura espontánea de la simetría, con la excepción de ciertas simetrías accidentales (por ejemplo, la formación de partículas virtuales pesadas, que solo ocurre a bajas temperaturas).
Parámetros de pedido
Un parámetro de orden es una medida del grado de orden entre los límites de un sistema de transición de fase; normalmente oscila entre cero en una fase (normalmente por encima del punto crítico) y distinto de cero en la otra. En el punto crítico, la susceptibilidad del parámetro de orden generalmente diverge.
Un ejemplo de un parámetro de orden es la magnetización neta en un sistema ferromagnético que experimenta una transición de fase. Para transiciones líquido/gas, el parámetro de orden es la diferencia de densidades.
Desde una perspectiva teórica, los parámetros de orden surgen de la ruptura de la simetría. Cuando esto sucede, es necesario introducir una o más variables adicionales para describir el estado del sistema. Por ejemplo, en la fase ferromagnética, se debe proporcionar la magnetización neta, cuya dirección se eligió espontáneamente cuando el sistema se enfrió por debajo del punto de Curie. Sin embargo, tenga en cuenta que los parámetros de orden también se pueden definir para transiciones que no rompen la simetría.
Algunas transiciones de fase, como la superconductora y la ferromagnética, pueden tener parámetros de orden para más de un grado de libertad. En tales fases, el parámetro de orden puede tomar la forma de un número complejo, un vector o incluso un tensor, cuya magnitud tiende a cero en la transición de fase.
También existen descripciones duales de transiciones de fase en términos de parámetros de desorden. Estos indican la presencia de excitaciones similares a líneas, como líneas de vórtices o defectos.
Relevancia en cosmología
Las transiciones de fase que rompen la simetría juegan un papel importante en la cosmología. A medida que el universo se expandió y se enfrió, el vacío experimentó una serie de transiciones de fase que rompieron la simetría. Por ejemplo, la transición electrodébil rompió la simetría SU(2)×U(1) del campo electrodébil en la simetría U(1) del campo electromagnético actual. Esta transición es importante para explicar la asimetría entre la cantidad de materia y antimateria en el universo actual, según la teoría de la bariogénesis electrodébil.
Las transiciones de fase progresivas en un universo en expansión están implicadas en el desarrollo del orden en el universo, como lo ilustra el trabajo de Eric Chaisson y David Layzer.
Véase también teorías del orden relacional y orden y desorden.
Exponentes críticos y clases de universalidad
Las transiciones de fase continuas son más fáciles de estudiar que las transiciones de primer orden debido a la ausencia de calor latente, y se ha descubierto que tienen muchas propiedades interesantes. Los fenómenos asociados a transiciones de fase continuas se denominan fenómenos críticos, debido a su asociación con puntos críticos.
Resulta que las transiciones de fase continuas se pueden caracterizar mediante parámetros conocidos como exponentes críticos. El más importante es quizás el exponente que describe la divergencia de la longitud de correlación térmica al acercarse a la transición. Por ejemplo, examinemos el comportamiento de la capacidad calorífica cerca de tal transición. Variamos la temperatura T del sistema mientras mantenemos fijas todas las demás variables termodinámicas y encontramos que la transición ocurre a alguna temperatura crítica Tc. Cuando T está cerca de Tc, la capacidad calorífica C normalmente tiene un comportamiento de ley de potencia:
- C∝ ∝ SilencioTc− − TSilencio− − α α .{displaystyle Cpropto SilencioT_{text{c}-T privacy^{-alpha }
La capacidad calorífica de los materiales amorfos tiene un comportamiento similar cerca de la temperatura de transición vítrea donde el exponente crítico universal α = 0.59 Un comportamiento similar, pero con el exponente ν en su lugar de α, se aplica a la longitud de correlación.
El exponente ν es positivo. Esto es diferente con α. Su valor real depende del tipo de transición de fase que estemos considerando.
Se cree ampliamente que los exponentes críticos son los mismos arriba y debajo de la temperatura crítica. Ahora se ha demostrado que esto no es necesariamente cierto: Cuando una simetría continua se rompe explícitamente a una simetría discreta por anisotropías irrelevantes (en el sentido del grupo de renormalización), entonces algunos exponentes (como γ γ {displaystyle gamma }, el exponente de la susceptibilidad) no son idénticos.
Para −1 < a < 0, la capacidad calorífica tiene un "torcedura" a la temperatura de transición. Este es el comportamiento del helio líquido en la transición lambda de un estado normal a un estado superfluido, para el cual los experimentos han encontrado α = −0.013 ± 0.003. Se realizó al menos un experimento en condiciones de gravedad cero de un satélite en órbita para minimizar las diferencias de presión en la muestra. Este valor experimental de α está de acuerdo con las predicciones teóricas basadas en la teoría de la perturbación variacional.
Para 0 < a < 1, la capacidad calorífica diverge a la temperatura de transición (aunque, dado que α < 1, la entalpía permanece finita). Un ejemplo de tal comportamiento es la transición de fase ferromagnética 3D. En el modelo de Ising tridimensional para imanes uniaxiales, los estudios teóricos detallados han arrojado el exponente α ≈ +0,110.
Algunos sistemas modelo no obedecen un comportamiento de ley de potencia. Por ejemplo, la teoría del campo medio predice una discontinuidad finita de la capacidad calorífica a la temperatura de transición y el modelo bidimensional de Ising tiene una divergencia logarítmica. Sin embargo, estos sistemas son casos límite y una excepción a la regla. Las transiciones de fase real exhiben un comportamiento de ley de potencia.
Varios otros exponentes críticos, β, γ, δ, ν y η, se definen examinando el comportamiento de la ley de potencia de una cantidad física medible cerca de la transición de fase. Los exponentes se relacionan mediante relaciones de escala, como
- β β =γ γ /()δ δ − − 1),.. =γ γ /()2− − .. ).{displaystyle beta =gamma /(delta -1),quad nu =gamma /(2-eta).}
Se puede demostrar que solo hay dos exponentes independientes, p. ν y η.
Es un hecho notable que las transiciones de fase que surgen en diferentes sistemas a menudo poseen el mismo conjunto de exponentes críticos. Este fenómeno se conoce como universalidad. Por ejemplo, se ha encontrado que los exponentes críticos en el punto crítico líquido-gas son independientes de la composición química del fluido.
Más impresionante, pero comprensible desde arriba, son una coincidencia exacta para los exponentes críticos de la transición de fase ferromagnética en imanes uniaxiales. Se dice que tales sistemas están en la misma clase de universalidad. La universalidad es una predicción de la teoría del grupo de renormalización de las transiciones de fase, que establece que las propiedades termodinámicas de un sistema cerca de una transición de fase dependen solo de un pequeño número de características, como la dimensionalidad y la simetría, y son insensibles a las propiedades microscópicas subyacentes de el sistema. Una vez más, la divergencia de la longitud de correlación es el punto esencial.
Fenómenos críticos
También hay otros fenómenos críticos; por ejemplo, además de las funciones estáticas también hay dinámicas críticas. Como consecuencia, en una transición de fase uno puede observar desaceleración crítica o aceleración. Conectado al fenómeno anterior está también el fenómeno de aumento de las fluctuaciones antes de la transición de fase, como consecuencia del menor grado de estabilidad de la fase inicial del sistema. Las grandes clases de universalidad estática de una transición de fase continua se dividen en clases de universalidad dinámica más pequeñas. Además de los exponentes críticos, también existen relaciones universales para ciertas funciones estáticas o dinámicas de los campos magnéticos y diferencias de temperatura del valor crítico.
Transiciones de fase en sistemas biológicos
Las transiciones de fase juegan muchos papeles importantes en los sistemas biológicos. Los ejemplos incluyen la formación de bicapa lipídica, la transición de glóbulos en espiral en el proceso de plegamiento de proteínas y fusión de ADN, transiciones similares a cristales líquidos en el proceso de condensación de ADN y unión cooperativa de ligandos a ADN y proteínas con el carácter de transición de fase.
En membranas biológicas, las transiciones de fase de gel a líquido cristalino desempeñan un papel fundamental en el funcionamiento fisiológico de las biomembranas. En la fase de gel, debido a la baja fluidez de las cadenas de acilo graso de los lípidos de la membrana, las proteínas de la membrana tienen un movimiento restringido y, por lo tanto, están restringidas en el ejercicio de su función fisiológica. Las plantas dependen críticamente de la fotosíntesis de las membranas tilacoides del cloroplasto que están expuestas a temperaturas ambientales frías. Las membranas tilacoides retienen la fluidez innata incluso a temperaturas relativamente bajas debido al alto grado de desorden de acilo graso permitido por su alto contenido de ácido linolénico, cadena de 18 carbonos con 3 dobles enlaces. La temperatura de transición de fase cristalina de gel a líquido de las membranas biológicas se puede determinar mediante muchas técnicas, incluidas la calorimetría, la fluorescencia, la resonancia paramagnética de electrones con etiquetas de espín y la RMN mediante el registro de mediciones del parámetro en cuestión en una serie de temperaturas de muestra. También se ha propuesto un método sencillo para su determinación a partir de las intensidades de línea de 13-C RMN.
Se ha propuesto que algunos sistemas biológicos podrían estar cerca de puntos críticos. Los ejemplos incluyen redes neuronales en la retina de la salamandra, bandadas de pájaros redes de expresión génica en Drosophila y plegamiento de proteínas. Sin embargo, no está claro si razones alternativas podrían o no explicar algunos de los fenómenos que respaldan los argumentos a favor de la criticidad. También se ha sugerido que los organismos biológicos comparten dos propiedades clave de las transiciones de fase: el cambio de comportamiento macroscópico y la coherencia de un sistema en un punto crítico. Las transiciones de fase son una característica destacada del comportamiento motor en los sistemas biológicos. Las transiciones espontáneas de la marcha, así como las desvinculaciones de tareas motoras inducidas por la fatiga, muestran un comportamiento crítico típico como una indicación del cambio cualitativo repentino del patrón de comportamiento motor previamente estable.
El rasgo característico de las transiciones de fase de segundo orden es la aparición de fractales en algunas propiedades sin escala. Durante mucho tiempo se ha sabido que los glóbulos de proteína se forman por interacciones con el agua. Hay 20 aminoácidos que forman grupos laterales en las cadenas peptídicas de proteínas que van desde hidrofílicos a hidrofóbicos, lo que hace que los primeros se encuentren cerca de la superficie globular, mientras que los últimos se encuentran más cerca del centro globular. Se descubrieron veinte fractales en áreas superficiales asociadas al disolvente de > 5000 segmentos de proteína. La existencia de estos fractales demuestra que las proteínas funcionan cerca de los puntos críticos de las transiciones de fase de segundo orden.
En grupos de organismos en estrés (al acercarse a transiciones críticas), las correlaciones tienden a aumentar, mientras que al mismo tiempo también aumentan las fluctuaciones. Este efecto está respaldado por muchos experimentos y observaciones de grupos de personas, ratones, árboles y plantas herbáceas.
Experimental
Se aplica una variedad de métodos para estudiar los diversos efectos. Los ejemplos seleccionados son:
- Thermogravimetry (muy común)
- Difracción de rayos X
- Difracción de neutrones
- Raman Spectroscopy
- SQUID (medición de las transiciones magnéticas)
- Efecto Hall (medición de las transiciones magnéticas)
- Espectroscopia Mössbauer (medición simultánea de transiciones magnéticas y no magnéticas. Limitado hasta aproximadamente 800–1000 °C)
- Correlación angular perturmada (medición simultánea de transiciones magnéticas y no magnéticas. No hay límites de temperatura. Más de 2000 °C ya realizada, teóricamente posible hasta el material de cristal más alto, como el carburo de hafnio de tantalio 4215 °C.)
Contenido relacionado
Nanosegundo
Masa reducida
Energía libre termodinámica