Transformada de Hilbert

En matemáticas y procesamiento de señales, el Hilbert transforma es un singular integral específico que toma una función, u()t) de una variable real y produce otra función de una variable real H(u)t). La transformación de Hilbert es dada por el valor principal de Cauchy de la revolución con la función ${displaystyle 1/(pi t)}$ (ver § Definición). La transformación de Hilbert tiene una representación particularmente simple en el dominio de frecuencia: Imparte un cambio de fase de ±90° (π/2 radios) a cada componente de frecuencia de una función, el signo del cambio dependiendo del signo de la frecuencia (ver § Relación con la transformación Fourier). La transformación de Hilbert es importante en el procesamiento de señales, donde es un componente de la representación analítica de una señal de valor real u()t). El transformado Hilbert fue introducido por primera vez por David Hilbert en este escenario, para resolver un caso especial del problema Riemann-Hilbert para funciones analíticas.

Definición

La transformada de Hilbert de u puede considerarse como la convolución de u(t) con la función h(t) = < span role="math" class="sfrac tion">1/< span class="texhtml mvar" style="font-style:italic;">πt, conocido como núcleo de Cauchy. Porque 1/t no es integrable en t = 0< /span>, la integral que define la convolución no siempre converge. En cambio, la transformada de Hilbert se define utilizando el valor principal de Cauchy (indicado aquí por p.v.). Explícitamente, la transformada de Hilbert de una función (o señal) u(t) viene dada por

$${displaystyle operatorname {H}(t)={frac {1}{pi) },operatorname {p.v.} int _{-infty }{+infty }{frac {u(tau)}{t-tau },mathrm {d} #$$

siempre que esta integral exista como valor principal. Esta es precisamente la convolución de u con la distribución templada p.v. 1/ πt. Alternativamente, al cambiar las variables, la integral del valor principal se puede escribir explícitamente como

$${displaystyle operatorname {H} (u)={frac {2}{pi },lim _{varepsilon to 0}int _{varepsilon - ¿Qué?$$

Cuando la transformada de Hilbert se aplica dos veces seguidas a una función u, el resultado es

$${displaystyle operatorname {H} {bigl (}operatorname {H} (u){bigr)}(t)=-u(t),}$$

siempre que las integrales que definen ambas iteraciones convergen en un sentido adecuado. En particular, la transformación inversa es ${displaystyle operatorname {H}$. Este hecho se puede ver fácilmente considerando el efecto de la transformación Hilbert en la transformación Fourier u()t) (ver § Relación con el Fourier transformar abajo).

Para una función analítica en el semiplano superior, la transformada de Hilbert describe la relación entre la parte real y la parte imaginaria de los valores límite. Es decir, si f(z) es analítico en el plano complejo medio superior {z: Soy{z} > 0}, y u(t) = Re{f (t + 0·i)}, luego Estoy{f(t + 0·i)} = H(u)(t) hasta una constante aditiva, siempre que exista esta transformada de Hilbert.

Notación

En el procesamiento de señales la transformación de Hilbert u()t) es comúnmente denotado por ${displaystyle {hat {u}(t)}$. Sin embargo, en matemáticas, esta notación ya se utiliza ampliamente para denotar la transformación Fourier de u()t). De vez en cuando, la transformación de Hilbert puede ser denotada por ${displaystyle {tilde {u}(t)}$. Además, muchas fuentes definen la transformación de Hilbert como el negativo de la definida aquí.

Historia

La transformación de Hilbert surgió en el trabajo de Hilbert de 1905 sobre un problema que Riemann planteaba sobre las funciones analíticas, que ha llegado a ser conocido como el problema Riemann-Hilbert. El trabajo de Hilbert estaba principalmente preocupado con la transformación de Hilbert para funciones definidas en el círculo. Algunos de sus trabajos anteriores relacionados con el Discreto Hilbert Transform se remontan a conferencias que dio en Göttingen. Los resultados fueron publicados posteriormente por Hermann Weyl en su tesis. Schur mejoró los resultados de Hilbert sobre la discreta transformación de Hilbert y los extendió al caso integral. Estos resultados se limitaron a los espacios L2 y l2. En 1928, Marcel Riesz demostró que la transformación de Hilbert puede definirse para u dentro ${displaystyle L^{p}(mathbb {R})}$ (Lp space) for 1 p ■, que la transformación de Hilbert es un operador atado en ${displaystyle L^{p}(mathbb {R})}$ para 1 p ■, y que resultados similares sostienen para la transformación Hilbert en el círculo, así como la discreta transforma Hilbert. La transformación de Hilbert fue un ejemplo motivador para Antoni Zygmund y Alberto Calderón durante su estudio de integrales singulares. Sus investigaciones han desempeñado un papel fundamental en el análisis armónico moderno. Varias generalizaciones de la transformación de Hilbert, como las transformaciones bilineales y trilineales de Hilbert, siguen siendo áreas activas de investigación hoy.

Relación con la transformada de Fourier

La transformada de Hilbert es un operador multiplicador. El multiplicador de H es σ_H(ω) = −i sgn(ω), donde sgn es la función signum. Por lo tanto:

$${displaystyle {mathcal {}{bigl (}operatorname {H} (u){bigr)}(omega)=-ioperatorname {sgn}(omega)cdot {mathcal {F}(u)(omega),}}$$

Donde ${displaystyle {fnMithcal}}$ denota la transformación Fourier. Desde sgn(x) = sgn(2)πx), sigue que este resultado se aplica a las tres definiciones comunes de ${displaystyle {fnMithcal}}$.

Según la fórmula de Euler,

$${displaystyle sigma _{operatorname {H}(omega)={begin{cases}~i=e^{+ipi /2}, ventaja{text{for }omega - ¿Por qué? =0,-i=e^{-ipi /2}, reducida{text{for }omega confidencial0.end{cases}}$$

Por lo tanto, H(u)(t) tiene el efecto de desplazar la fase de los componentes de frecuencia negativos. de u(t) por +90° (< span class="num">π⁄2< /span> radianes) y la fase de los componentes de frecuencia positivos en −90°, y i·H(u)(t) tiene el efecto de restaurar los componentes de frecuencia positivos mientras desplaza los de frecuencia negativa +90° adicionales, lo que resulta en su negación (es decir, una multiplicación por −1).

Cuando la transformada de Hilbert se aplica dos veces, la fase de los componentes de frecuencia negativos y positivos de u(t) se desplazan respectivamente +180° y −180°, que son cantidades equivalentes. La señal es negada; es decir, H(H(u)) = −u, porque

$${displaystyle left(sigma ##{2}=e^{pm ipi }=-1quad {text{for }omega neq 0.}$$

Tabla de transformadas de Hilbert seleccionadas

En la tabla siguiente, el parámetro de frecuencia ${displaystyle omega }$ es real.

Signal ${displaystyle u(t)}$	Hilbert transforma ${displaystyle operatorname {H} (u)(t)}$
${displaystyle sin(omega t+varphi)}$	${displaystyle {begin{lll}sin left(omega t+varphi -{tfrac {pi }{2}right)=-cos left(omega t+varphi right),quad omega √0\\sinleft(omega t+varphi +{tfrac {pi }right)=cos left(omega t+varphi right),quad omega י0end{array}}}$
${displaystyle cos(omega t+varphi)}$	${displaystyle {begin{lll}cos left(omega t+varphi -{tfrac {pi }{2}right)=sin left(omega t+varphi right),quad omega #####cosleft(omega t+varphi +{tfrac {pi }{2}right)=-sin left(omega t+varphi right),quad omega י0end{array}}}}$
${displaystyle e^{iomega t}$	${displaystyle {begin{lll}e^{ileft(omega t-{tfrac {pi} }{2}right)}quad omega ################################################################################################################################################################################################################################################################$
${displaystyle e^{-iomega t}$	${displaystyle {begin{lll}e^{-ileft(omega t-{tfrac {pi} }{2}right)},quad omega } {2}derecha)},quad omega$
${displaystyle 1 over t^{2}+1}$	${displaystyle t over t^{2}+1}$
${displaystyle e^{-t^{2}}$	${displaystyle {frac {2}{sqrt {pi}}}F(t)}$ (ver función Dawson)
Función de Sinc ${displaystyle sin(t) over t}$	${displaystyle 1-cos(t) over t}$
Función Dirac delta ${displaystyle delta (t)}$	${displaystyle {1 over pi t}$
Función característica ${displaystyle chi _{[a,b}(t)}$	${displaystyle {frac {fnMicroc}{,pi}lnleftvert {fracfnMicroc} {t-a}{t-b}rightvert}$

Notas

Hay disponible una tabla extensa de transformadas de Hilbert. Tenga en cuenta que la transformada de Hilbert de una constante es cero.

Dominio de definición

No es obvio que la transformación de Hilbert esté bien definida, ya que la definición integral inadecuada debe converger en un sentido adecuado. Sin embargo, la transformación de Hilbert está bien definida para una amplia clase de funciones, a saber, las de ${displaystyle L^{p}(mathbb {R})}$ para 1 p ■.

Más precisamente, si u está dentro. ${displaystyle L^{p}(mathbb {R})}$ para 1 p ■, entonces el límite que define la integral inadecuada

$${displaystyle operatorname {H} (u)={frac {2}{pi) }lim _{varepsilon to 0}int _{varepsilon ¿Qué?$$

existe para casi todos t. La función límite también está en ${displaystyle L^{p}(mathbb {R})}$ y es de hecho el límite en la media de la integral inadecuada también. Eso es,

$${displaystyle {frac {2}{pi}}int _{varepsilon }{infty }{frac {u(t-tau)-u(t+tau)}{2tau },mathrm {d} tau to operatorname {H} (u)}(t)}$$

como ε → 0 en L^p norma, así como puntualmente en casi todas partes, por el teorema de Titchmarsh.

En el caso p = 1, la transformada de Hilbert todavía converge puntualmente en casi todas partes, pero puede no ser integrable, incluso localmente. En particular, la convergencia en la media no ocurre en general en este caso. Sin embargo, la transformada de Hilbert de una función L¹ converge en L¹-débil, y la transformada de Hilbert es un operador acotado de L¹ a L^1,w. (En particular, dado que la transformada de Hilbert también es un operador multiplicador en L², la interpolación de Marcinkiewicz y un argumento de dualidad proporcionan una prueba alternativa de que H está limitado por L ^p.)

Propiedades

Limitación

Si 1 p ■, entonces el Hilbert se transforma en ${displaystyle L^{p}(mathbb {R})}$ es un operador lineal vinculado, lo que significa que existe una constante C_p tales que

$${displaystyleleftfnMicrosoftfnMicrosoft {H}Urightspefnh}p}leq ¿Qué?$$

para todos ${displaystyle uin L^{p}(mathbb {R})}$.

La mejor constante ${displaystyle C_{p}$ es dado por

$${displaystyle C_{p}={begin{cases}tan {frac {pi {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {fnMicroc {pi} {2p}} {text{for}~2 Se hizo \infty.end{cases}}$$

Una manera fácil de encontrar la mejor ${displaystyle C_{p}$ para ${displaystyle p}$ ser un poder de 2 es a través de la llamada identidad de Cotlar que ${displaystyle (operatorname) [H} f)^{2}=f^{2}+2operatorname {H} (foperatorname {H} f)}$ para todo valor real f. Las mismas mejores constantes sostienen para la transformación periódica de Hilbert.

La atadura de la transformación de Hilbert implica la ${displaystyle L^{p}(mathbb {R})}$ convergencia del operador de suma parcial simétrica

$${displaystyle S_{R}f=int ¿Por qué?$$

a f dentro ${displaystyle L^{p}(mathbb {R})}$.

Anti-autoadjunción

La transformación de Hilbert es un operador anti-self adjoint relativo a la unión de dualidad entre ${displaystyle L^{p}(mathbb {R})}$ y el espacio dual ${displaystyle L^{q}(mathbb {R})}$, Donde p y q son Hölder conjugados y 1 p, q ■. Simbólicamente,

$${displaystyle langle operatorname Oh, Dios.$$

para ${displaystyle uin L^{p}(mathbb {R})}$ y ${displaystyle vin L^{q}(mathbb {R})}$.

Transformación inversa

La transformada de Hilbert es una anti-involución, lo que significa que

$${displaystyle operatorname {H} {bigl (}operatorname {H} left(uright){bigr)}=-u}$$

siempre que cada transformación esté bien definida. Desde H preserva el espacio ${displaystyle L^{p}(mathbb {R})}$, esto implica en particular que la transformación de Hilbert es invertible ${displaystyle L^{p}(mathbb {R})}$, y eso

$${displaystyle operatorname [H] ^{-1}=-operatorname {H}$$

Estructura compleja

Porque... H² I (""I"es el operador de identidad) en el espacio real de Banach real- Funciones valoradas ${displaystyle L^{p}(mathbb {R})}$, el transformado Hilbert define una estructura lineal compleja en este espacio de Banach. En particular, cuando p = 2, el transformado Hilbert da el espacio Hilbert de funciones reales en ${displaystyle L^{2}(mathbb {R})}$ la estructura de un complejo Hilbert espacio.

Los estados propios (complejos) de la transformada de Hilbert admiten representaciones como funciones holomorfas en los semiplanos superior e inferior en el espacio de Hardy H2 según el teorema de Paley-Wiener.

Diferenciación

Formalmente, la derivada de la transformada de Hilbert es la transformada de Hilbert de la derivada, es decir, estos dos operadores lineales conmutan:

$${displaystyle operatorname {H}left({frac {mathrm {d}{mathrm {d} t}}}right)={frac {mathrm {d} {mathrm {d} t}operatorname {H} (u)}}}}}} {f}}$$

Iterando esta identidad,

$${displaystyle operatorname {H} left({frac {mathrm {d} ^{k}u}{mathrm {d} t^{k}}}}right)={frac {mathrm {d} {} {m}{k}}}}}}}operatorname {H} (u)} {f} {f} {f} {f}} {f}}} {f} {f} {f} {f} {f}}} {f}}}}}} {f} {f}}} {f}}}}}}}} {f} {f}}}} {f} {f}}} {f}}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$$

Esto es rigurosamente cierto como se establece u y su primera k derivados pertenecen a ${displaystyle L^{p}(mathbb {R})}$. Uno puede comprobar esto fácilmente en el dominio de frecuencia, donde la diferenciación se convierte en multiplicación por ⋅.

Convoluciones

La transformada de Hilbert se puede realizar formalmente como una convolución con la distribución templada

$${displaystyle h(t)=operatorname {p.v.} {frac {1}{pi ,t}}$$

Por lo tanto, formalmente,

$${displaystyle operatorname {H} (u)=h*u}$$

Sin embargo, a priori esto sólo puede definirse para u una distribución de soporte compacto. Es posible trabajar con cierto rigor con esto ya que las funciones compatibles de forma compacta (que son distribuciones a fortiori) son densas en L^p . Alternativamente, se puede utilizar el hecho de que h(t) es la derivada distribucional de la función log|t|/π; esto es

$${displaystyle operatorname {H}(u)={frac {mathrm {d}{mathrm {d}}left({frac {1}{pi }}left(u*log {bigl ANTERI}cdot {bigr Н}right)right)$$

Para la mayoría de los propósitos operativos, la transformada de Hilbert se puede tratar como una convolución. Por ejemplo, en un sentido formal, la transformada de Hilbert de una convolución es la convolución de la transformada de Hilbert aplicada a sólo uno de cualquiera de los factores:

$${displaystyle operatorname [H} (u*v)=operatorname {H} (u)*v=u*operatorname {H} (v)}$$

Esto es rigurosamente cierto si u y v son distribuciones con soporte compacto ya que, en ese caso,

$${displaystyle h*(u*v)=(h*u)*v=u*(h*v)}$$

Al pasar a un límite apropiado, también es cierto si u ∈ L^p< /span> y v ∈ L^q siempre que

$${displaystyle 1 {1}{}+{frac} {1}{q}}$$

de un teorema debido a Titchmarsh.

Invariancia

El transformado Hilbert tiene las siguientes propiedades de invariancia en ${displaystyle L^{2}(mathbb {R})}$.

• Se comunica con traducciones. Es decir, se comunica con los operadores T_a f()x) f()x + a) para todos a dentro ${displaystyle mathbb {R}$
• Se comunica con dilaciones positivas. Eso es que se comunica con los operadores M_λ f ()x) f ()λ x) para todos λ ■ 0.
• Anticommuta con la reflexión Rf ()x) f () -x).

Hasta una constante multiplicativa, la transformada de Hilbert es el único operador acotado en L² con estas propiedades.

De hecho hay un conjunto más amplio de operadores que se comunican con la transformación de Hilbert. El grupo ${displaystyle {text{SL}(2,mathbb {R})}$ actos por operadores unitarios U_g sobre el espacio ${displaystyle L^{2}(mathbb {R})}$ por la fórmula

$${displaystyle operatorname {fnMicrosoft Sans Serif}ffnMicroc {1}cx+d},fleft({frac] {ax+b}{cx+d}derecha),qquad g={begin{bmatrix}a limitbc limitdend{bmatrix}~,qquad {text{ for }~ad-bc=pm 1.}$$

Esta representación unitaria es un ejemplo de una representación de serie principal ${displaystyle ~{text{SL}}(2,mathbb {R}~.}$ En este caso es reducible, dividiendo como la suma ortogonal de dos subespacios invariantes, Hardy espacio ${displaystyle H^{2}(mathbb {R})}$ y su conjugado. Estos son los espacios de L² Valores de límites de las funciones holomorfas en los planos superior e inferior. ${displaystyle H^{2}(mathbb {R})}$ y su conjugado consisten exactamente en L² funciones con Fourier transforma desapareciendo en las partes negativas y positivas del eje real respectivamente. Desde la transformación de Hilbert es igual a H =i (22)P I - ICon P ser la proyección ortogonal de ${displaystyle L^{2}(mathbb {R})}$ sobre ${displaystyle operatorname {H} ^{2}(mathbb {R}),}$ y I el operador de identidad, sigue que ${displaystyle operatorname {H} ^{2}(mathbb {R})}$ y su complemento ortogonal son eigenspaces de H para los eigenvalues ±i. En otras palabras, H comunicaciones con los operadores U_g. Las restricciones de los operadores U_g a ${displaystyle operatorname {H} ^{2}(mathbb {R})}$ y su conjugado dan representaciones irreducibles de ${displaystyle {text{SL}(2,mathbb {R})}$ – el llamado límite de las representaciones discretas de la serie.

Ampliando el dominio de la definición

Transformada de Hilbert de distribuciones

Además, es posible extender la transformada de Hilbert a ciertos espacios de distribuciones (Pandey 1996, Capítulo 3). Dado que la transformada de Hilbert conmuta con diferenciación y es un operador acotado en L^p, H restringe para dar una transformación continua en el límite inverso de los espacios de Sobolev:

$${displaystyle {mthcal {}_{L^{p}={underset {ntoinfty}{compset {longleftarrow }{lim }}W^{n,p}(mathbb {R}}}}}$$

La transformación de Hilbert se puede definir en el espacio dual ${fnK} {fnMitcal}} {fnK}} {fnK}}} {fnK}}}$, denotado ${fnMicrosoft Sans}$, que consiste en L^p distribuciones. Esto se logra por la parización de la dualidad:
Para ${displaystyle uin {fn\\fnMitcal {D}_{L^{p}}$, definir:

$${displaystyle operatorname {H} (u)in {mathcal {D}'_{L^{p}=langle operatorname {H} u,vrangle \triangleq \langle u,-operatorname {H} vrangle {text{for all} vin {mathcal {D}_{L^{p}}}$$

También es posible definir la transformada de Hilbert en el espacio de distribuciones templadas mediante un enfoque debido a Gel'fand y Shilov, pero se necesita mucho más cuidado debido a la singularidad de la integral.

Transformada de Hilbert de funciones acotadas

La transformación de Hilbert se puede definir para funciones en ${displaystyle L^{infty}(mathbb {R})}$ también, pero requiere algunas modificaciones y cavernas. Entendidas adecuadamente, el Hilbert transforma mapas ${displaystyle L^{infty}(mathbb {R})}$ al espacio de Banach de clases de oscilación media (BMO).

Interpretada ingenuamente, la transformada de Hilbert de una función acotada está claramente mal definida. Por ejemplo, con u = sgn(x), la integral que define H(u) diverge en casi todas partes a ±∞. Para aliviar tales dificultades, la transformada de Hilbert de una función L^∞ se define mediante la siguiente forma regularizada de la integral

$${displaystyle operatorname {H}(u)=operatorname {p.v.} int _{-infty }^{infty }u(tau)left{h(t-tau)-h_{0}(-tau)right},mathrm {d}tau }$$

donde como arriba h(x) = 1/πx< /span> y

$${displaystyle h_{0}(x)={begin{cases}0 limitada{text{for}~ perpetuax impertine1\{frac {1}{pipi,x}} {text{for}~Principalmente*}$$

La transformada modificada H concuerda con la transformada original hasta una constante aditiva en funciones de soporte compacto a partir de un resultado general de Calderón y Zygmund. Además, la integral resultante converge puntualmente en casi todas partes, y con respecto a la norma BMO, a una función de oscilación media acotada.

Un resultado profundo del trabajo de Fefferman es que una función es de oscilación media atada si y sólo si tiene la forma f + H(g) para algunos ${displaystyle f,gin L^{infty}(mathbb {R})}$.

Funciones conjugadas

La transformada de Hilbert se puede entender en términos de un par de funciones f(x) y g(x) tal que la función

$${displaystyle F(x)=f(x)+i,g(x)}$$

Supongamos que ${displaystyle fin L^{p}(mathbb {R}).}$ Entonces, por la teoría de la integral Poisson, f admite una extensión armónica única en el medio plano superior, y esta extensión es dada por

$${displaystyle u(x+iy)=u(x,y)={frac {1}{pi }int _{-infty }{infty }f(s);{frac {y}{(x-s)^{2}+y^{2}}}}}};mathrm {d} s} {} {} {} {}{}}}}}}}}}}}}}}}}}}}}}} {$$

que es la convolución de f con el núcleo Poisson

$${displaystyle P(x,y)={frac {y}{pi ,left(x^{2}+y^{2}right)}}}$$

Además, existe una función armónica única v definida en el semiplano superior tal que F(z) = u(z) + i v(< i>z) es holomorfa y

$${displaystyle lim _{yto infty }v,(x+i,y)=0}$$

Esta función armónica se obtiene de f tomando una convolución con el núcleo de Poisson conjugado

$${displaystyle Q(x,y)={frac {x}{pi ,left(x^{2}+y^{2}right)}}}$$

Así

$${fnMicrosoft Sans Serif} {fnMicroc {fnMicroc} {fnMicrosoft Sans Serif} {fnMicroc {x-s}{,(x-s)}{2}+y^{2},}}};mathrm {d} s.}$$

De hecho, las partes real e imaginaria del núcleo de Cauchy son

$${displaystyle {frac {i}{pi,z}=P(x,y)+i,Q(x,y)}$$

de modo que F = u + i v es holomórfico según Cauchy' s fórmula integral.

La función v obtenida de u de esta manera se llama conjugado armónico de u. El límite límite (no tangencial) de v(x,y) como < span class="texhtml">y → 0 es la transformada de Hilbert de f. Así, sucintamente,

$${displaystyle operatorname {H} (f)=lim _{yto 0}Q(-,y)star f}$$

Teorema de Titchmarsh

El teorema de Titchmarsh (llamado así por E. C. Titchmarsh, quien lo incluyó en su trabajo de 1937) precisa la relación entre los valores límite de funciones holomorfas en el semiplano superior y la transformada de Hilbert. Proporciona las condiciones necesarias y suficientes para que una función integrable al cuadrado de valores complejos F(x) en la recta real ser el valor límite de una función en el espacio de Hardy H²(U) de funciones holomorfas en la mitad superior plano U.

El teorema afirma que las siguientes condiciones para una función cuadrada de valor complejo ${displaystyle F:mathbb {R} to mathbb {C}$ son equivalentes:

• F()x) es el límite como z → x de una función holomorfa F()z) en el medio plano superior tal que
  $${displaystyle int _{-infty}{infty } WordPressF(x+i,y)$$

  
• Las partes reales e imaginarias de F()x) Hilbert se transforma el uno del otro.
• La transformación de Fourier ${displaystyle {mathcal}(F)(x)}$ desaparece para x 0.

Un resultado más débil es cierto para funciones de clase Lp para p > 1. Específicamente, si F(z) es una función holomorfa tal que

$${displaystyle int _{-infty}{infty } WordPressF(x+i,y)$$

para todos Sí., entonces hay una función de valor complejo F()x) dentro ${displaystyle L^{p}(mathbb {R})}$ tales que F()x + i) → F()x) en el L^p norma como Sí. → 0 (así como mantener el punto de vista casi por todas partes). Además,

$${displaystyle F(x)=f(x)-i,g(x)}$$

Donde f es una función de valor real en ${displaystyle L^{p}(mathbb {R})}$ y g es el transformado Hilbert (de clase L^p) de f.

Esto no es cierto en el caso p = 1. De hecho, la transformada de Hilbert de una función L¹ f no necesita converger en el medio con otra función L¹. Sin embargo, la transformada de Hilbert de f converge casi en todas partes a una función finita g tal que

$${displaystyle int _{-infty }{infty }{frac { imperdong(x) habit^{p}{1+x^{2}}};mathrm {d} xinginfty }$$

Este resultado es directamente análogo a uno de Andrey Kolmogorov para las funciones de Hardy en el disco. Aunque generalmente se le llama teorema de Titchmarsh, el resultado agrega mucho trabajo de otros, incluidos Hardy, Paley y Wiener (ver Teorema de Paley-Wiener), así como el trabajo de Riesz, Hille y Tamarkin.

Problema de Riemann-Hilbert

Una forma del problema de Riemann-Hilbert busca identificar pares de funciones F₊ y F₋ tal que F₊ es holomorfo en el semiplano superior y F_- es holomorfo en el semiplano inferior, tal que para x a lo largo del eje real,

$${displaystyle F_{+}(x)-F_{-}(x)=f(x)}$$

Donde f()x) es una función de valor real dada ${displaystyle xin mathbb {R}$. El lado izquierdo de esta ecuación puede ser entendido como la diferencia de los límites F_± de los medio-planos apropiados, o como una distribución de hiperfunción. Dos funciones de esta forma son una solución del problema Riemann-Hilbert.

Formalmente, si F_± resuelve el problema de Riemann-Hilbert

$${displaystyle f(x)=F_{+}(x)-F_{-}(x)}$$

entonces la transformada de Hilbert de f(x) viene dada por

$${displaystyle H(f)(x)=-i{bigl (}F_{+}(x)+F_{-}(x){bigr)}.}$$

Transformada de Hilbert en el círculo

Para una función periódica f se define la transformada circular de Hilbert:

$${displaystyle {tilde {f}(x)triangleq {frac}{2pi} ¿Por qué?$$

La transformada circular de Hilbert se utiliza para caracterizar el espacio de Hardy y en el estudio de la función conjugada en series de Fourier. el núcleo,

$${displaystyle cot left({frac {x-t}right)}$$

El núcleo de Hilbert (para la transformada circular de Hilbert) se puede obtener haciendo que el núcleo de Cauchy sea 1⁄x periódico. Más precisamente, para x ≠ 0

$${displaystyle {frac {1}{,2,}}cot left({frac {x}{2}}right)={frac {1}{x}}+sum _{n=1}{infty }left({frac {1}{x+2npi ¿Qué?$$

Se pueden derivar muchos resultados sobre la transformada circular de Hilbert a partir de los resultados correspondientes a la transformada de Hilbert a partir de esta correspondencia.

Otra conexión más directa la proporciona la transformada de Cayley C(x) = (x – i) / (x + i), que lleva la línea real al círculo y el semiplano superior a la unidad disco. Induce un mapa unitario.

$${displaystyle U,f(x)={frac {1}{(x+i),{sqrt {pi }}},fleft(Cleft(xright)}}$$

de L²()T) sobre ${displaystyle L^{2}(mathbb {R}).}$ El operador U lleva el espacio Hardy H²()T) sobre el espacio Hardy ${displaystyle H^{2}(mathbb {R})}$.

Transformada de Hilbert en procesamiento de señales

Teorema de Bedrosiano

El teorema de Bedrosian establece que la transformada de Hilbert del producto de una señal de paso bajo y una señal de paso alto con espectros que no se superponen viene dada por el producto del paso bajo señal y la transformada de Hilbert de la señal de paso alto, o

$${displaystyle operatorname {H} left(f_{text{LP}(t)cdot f_{text{HP}(t)right)=f_{text{LP}(t)cdot operatorname {H} left(f_{text{HP}(t)right),}$$

donde f_LP y f< sub>HP son las señales de paso bajo y alto respectivamente. Una categoría de señales de comunicación a la que esto se aplica se denomina modelo de señal de banda estrecha. Un miembro de esa categoría es la modulación de amplitud de una "portadora" sinusoidal de alta frecuencia:

$${displaystyle u(t)=u_{m}(t)cdot cos(omega t+varphi),}$$

donde u_m(t) es el estrecho ancho de banda "mensaje" forma de onda, como voz o música. Luego por el teorema de Bedrosian:

$${displaystyle operatorname {H} (u)={begin{cases}+u_{m}(t)cdot sin(omega t+varphi), limitomega √0,\-u_{m}(t)cdot sin(omega t+varphi), limiteomega } {}} {end{cases}}} {$$

Representación analítica

Un tipo específico de función conjugada es:

$${displaystyle u_{a}(t)triangleq u(t)+icdot H(u)(t),}$$

conocido como representación analítica de ${displaystyle u(t).}$ El nombre refleja su aparato matemático, debido en gran medida a la fórmula de Euler. Aplicando el teorema de Bedrosian al modelo de banda angosta, la representación analítica es:

${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}$

()Eq.1)

Una propiedad de transformación de Fourier indica que esta compleja operación heterodina puede desplazar todos los componentes de frecuencia negativos de u_m(t) por encima de 0 Hz. En ese caso, la parte imaginaria del resultado es una transformada de Hilbert de la parte real. Esta es una forma indirecta de producir transformadas de Hilbert.

Modulación de ángulo (fase/frecuencia)

La forma:

$${displaystyle u(t)=Acdot cos(omega t+varphi _{m}(t)}$$

se llama modulación de ángulo, que incluye modulación de fase y modulación de frecuencia. La frecuencia instantánea es${displaystyle omega +varphi _{prime }(t).}$Para lo suficientemente grande ⋅, en comparación con ${displaystyle varphi _{prime }$:

$${displaystyle operatorname {H} (u)(t)approx Acdot sin(omega t+varphi _{m}(t)}}$$

$${displaystyle u_{a}(t)approx Acdot e^{i(omega t+varphi _{m}(t)}$$

Modulación de banda lateral única (SSB)

Cuando u_m(t) en La Ec.1 también es una representación analítica (de una forma de onda de mensaje), es decir:

$${displaystyle u_{m}(t)=m(t)+icdot {widehat {m}(t)}$$

el resultado es una modulación de banda lateral única:

$${displaystyle u_{a}(t)=(m(t)+icdot {widehat {m}(t)cdot e^{i(omega t+varphi)}}$$

cuyo componente transmitido es:

$${displaystyle {begin{aligned}u(t) {Re} {u_{a}(t)}\\cdotcdot cos(omega t+varphi)-{widehat {m}(t)cdot sin(omega t+varphi)end{aligned}}}}}$$

Causalidad

La función ${displaystyle h(t)=1/(pi t)}$ presenta dos desafíos basados en la causalidad para la aplicación práctica en una convolución (además de su valor indefinido a 0):

• Su duración es infinita (técnicamente Apoyo infinito). Finite-length ventana reduce el rango de frecuencia eficaz de la transformación; las ventanas más cortas resultan en mayores pérdidas en frecuencias bajas y altas. Vea también filtro de cuadratura.
• Es un filtro no-causal. Así que una versión retrasada, ${displaystyle h(t-tau),}$ es necesario. La producción correspondiente se retrasa posteriormente ${displaystyle tau.}$ Al crear la parte imaginaria de una señal analítica, la fuente (parte real) también debe retrasarse ${displaystyle tau }$.

Transformada discreta de Hilbert

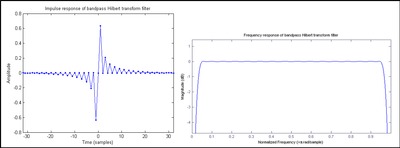
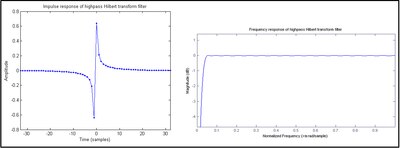
Para una función discreta, ${displaystyle u[n]}$, con transformación de Fourier discreta (DTFT), ${displaystyle U(omega)}$, y discreta Hilbert transform ${displaystyle {hat {u}[n]}$, el DTFT ${displaystyle {hat {u}[n]}$ en la región −π ► π es dado por:

${displaystyle operatorname {DTFT} ({hat {u})=U(omega)cdot (-icdot operatorname {sgn}(omega)). }$

La DTFT inversa, usando el teorema de convolución, es:

${displaystyle {begin{aligned}{hat {u} {n]} {scriptstyle mathrm {DTFT} [{-1}}(U(omega) *scriptstyle mathrm {DTFT} {-1}(-icdot operatorname {sgn}(omega)\ *frac {1}{2pi}int _{-pi }{pi }(-icdot operatorname {sgn}(omega)cdot e^{iomega n},mathrm {d}omega \cnunu[n] * underbrace {{frac {1}{2pi. _{-pi }{0}icdot e^{iomega n},mathrm {d} omega -int _{0}pi }icdot e^{iomega n},mathrm {d} omega right]} _{h[n]}},end{aligned}}}}}}}}$

dónde

${displaystyle h[n]\triangleq {begin{cases}0, reducida{text{for }n{ even}\\frac {2}{pi n}} {text{for }n{text{ odd}}}}}end{cases}}}}}}}}}}}}}} {$

que es una respuesta de impulso infinito (IIR). Cuando la convolución se realiza numéricamente, se sustituye h[n] por una aproximación FIR, como se muestra en Figura 1. Un filtro FIR con un número impar de coeficientes antisimétricos se denomina Tipo III y exhibe inherentemente respuestas de magnitud cero en las frecuencias 0 y Nyquist, lo que da como resultado en este caso una forma de filtro de paso de banda. En la Figura 2 se muestra un diseño de Tipo IV (número par de coeficientes antisimétricos). Dado que la respuesta de magnitud en la frecuencia de Nyquist no desaparece, se aproxima un poco mejor a un transformador Hilbert ideal que el filtro de derivaciones impares. Sin embargo

• Un típico (es decir, correctamente filtrado y muestreado) u[n] secuencia no tiene componentes útiles en la frecuencia Nyquist.
• La respuesta del impulso Tipo IV requiere un 1.2 cambio de muestra en el h[n] secuencia. Esto hace que los coeficientes de valor cero se conviertan en no cero, como se ve en Gráfico 2. Así que un diseño Tipo III es potencialmente el doble de eficiente que Tipo IV.
• El retraso del grupo de un diseño Tipo III es un número entero de muestras, lo que facilita la alineación ${displaystyle {hat {u}[n]}$ con ${displaystyle u[n],}$ crear una señal analítica. El retraso del grupo del tipo IV está a mitad de camino entre dos muestras.

La función MATLAB, hilbert(u,N), convoluciona una secuencia u[n] con la suma periódica:

${displaystyle h_{N}[n] triangleq sum _{m=-infty } {infty }h[n-mN]}$

y devuelve un ciclo (N muestras) del resultado periódico en la parte imaginaria de una secuencia de salida de valor complejo. La convolución se implementa en el dominio de frecuencia como el producto de la matriz${displaystyle {scriptstyle mathrm {DFT}left(u[n]right)}$con muestras de −i sgn(⋅) distribución (cuyos componentes reales e imaginarios son sólo 0 o±1). Gráfico 3 compara un medio ciclo de h_N[n] con una porción de longitud equivalente h[n]. Dada una aproximación FIR para ${displaystyle h[n],}$ denotado por ${displaystyle {tilde {h}[n],}$ sustitución ${displaystyle {scriptstyle mathrm {}left({tilde {h}[n]right)}$ para el −i sgn(⋅) muestra resultados en una versión FIR de la convolución.

La parte real de la secuencia de salida es la secuencia de entrada original, de modo que la salida compleja es una representación analítica de u[n]. Cuando la entrada es un segmento de un coseno puro, la convolución resultante para dos valores diferentes de N se muestra en la Figura 4 (parcelas rojas y azules). Los efectos de borde impiden que el resultado sea una función sinusoidal pura (gráfico verde). Dado que h_N[n] no es una FIR secuencia, el alcance teórico de los efectos es la secuencia de salida completa. Pero las diferencias con una función seno disminuyen con la distancia a los bordes. El parámetro N es la longitud de la secuencia de salida. Si excede la longitud de la secuencia de entrada, la entrada se modifica agregando elementos de valor cero. En la mayoría de los casos, eso reduce la magnitud de las diferencias. Pero su duración está dominada por los tiempos inherentes de subida y bajada de la respuesta al impulso h[n].

Es importante apreciar los efectos de borde cuando se utiliza un método llamado overlap-save para realizar la convolución en un u largo. [n] secuencia. Los segmentos de longitud N están convolucionados con la función periódica:

${fnMicrosoft Sans Serif} triangleq sum _{m=-infty }{infty }{tilde {h}[n-mN].}$

Cuando la duración de los valores no cero de ${displaystyle {tilde {h}[n]}$ es ${displaystyle M:$ la secuencia de salida incluye N − M + 1 muestras de ${displaystyle {hat {u}}}$ M − 1 las salidas se descartan de cada bloque de N, y los bloques de entrada se superponen por esa cantidad para evitar lagunas.

Figura 5 es un ejemplo del uso de la función IIR hilbert(·) y la aproximación FIR. En el ejemplo, se crea una función seno calculando la transformada discreta de Hilbert de una función coseno, que se procesó en cuatro segmentos superpuestos y se volvió a unir. Como muestra el resultado FIR (azul), las distorsiones aparentes en el resultado IIR (rojo) no son causadas por la diferencia entre h[n] y h_N[n] (verde y rojo en Figura 3). El hecho de que h_N[n] sea cónico (ventana) es realmente útil en este contexto. El verdadero problema es que no tiene suficientes ventanas. Efectivamente, M = N, mientras que el método de guardado y superposición necesita M < N.

Transformada de Hilbert en teoría de números

La transformada de Hilbert teórica de números es una extensión de la transformada de Hilbert discreta a números enteros módulo un número primo apropiado. En esto se sigue la generalización de la transformada discreta de Fourier a transformadas teóricas de números. La transformada de Hilbert de teoría de números se puede utilizar para generar conjuntos de secuencias discretas ortogonales.

Citas de páginas