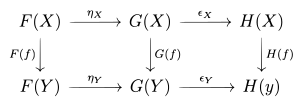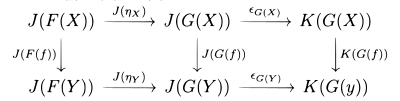Transformación natural

ImprimirCitar

Objeto central del estudio en la teoría de la categoría

En la teoría de categorías, una rama de las matemáticas, una transformación natural proporciona una forma de transformar un funtor en otro respetando la estructura interna (es decir, la composición de morfismos) de las categorías involucradas. Por lo tanto, una transformación natural puede considerarse como un "morfismo de funtores". De manera informal, la noción de una transformación natural establece que un mapa particular entre funtores se puede hacer consistentemente sobre una categoría completa.

De hecho, esta intuición se puede formalizar para definir las llamadas categorías de funtores. Las transformaciones naturales son, después de las categorías y los funtores, una de las nociones más fundamentales de la teoría de categorías y, en consecuencia, aparecen en la mayoría de sus aplicaciones.

Definición

Si $F$ y $G$ son functores entre las categorías $C$ y $D$ , entonces un transformación natural $eta$ desde $F$ a $G$ es una familia de morfismos que satisface dos requisitos.

La transformación natural debe asociarse a cada objeto $X$ dentro $C$ , un morfismo ${displaystyle eta _{X}:F(X)to G(X)}$ entre objetos $D$ . El morfismo ${displaystyle eta _{X}}$ se llama componente de $eta$ a $X$ .
Los componentes deben ser tales que para cada morfismo ${displaystyle f:Xto Y}$ dentro $C$ tenemos:

eta_Y circ F(f) = G(f) circ eta_X

La última ecuación se puede expresar convenientemente mediante el diagrama conmutativo

Si ambos $F$ y $G$ son contravariantes, las flechas verticales en el diagrama derecho se revierten. Si $eta$ es una transformación natural $F$ a $G$ , también escribimos ${displaystyle eta:Fto G}$ o ${displaystyle eta:FRightarrow G}$ . Esto también se expresa diciendo la familia de los morfismos ${displaystyle eta _{X}:F(X)to G(X)}$ es naturales naturales dentro $X$ .

Si, por cada objeto $X$ dentro ${displaystyle C}$ , el morfismo ${displaystyle eta _{X}}$ es un isomorfismo en $D$ , entonces $eta$ se dice que es un isomorfismo natural (o a veces equivalencia natural o isomorfismo de functores). Dos functores $F$ y $G$ se llaman naturalmente isomorfo o simplemente isomorfo si existe un isomorfismo natural $F$ a $G$ .

An transformación infranatural $eta$ desde $F$ a $G$ es simplemente una familia de morfismos ${displaystyle eta _{X}:F(X)to G(X)}$ , para todos $X$ dentro $C$ . Así una transformación natural es una transformación infranatural para la cual ${displaystyle eta _{Y}circ F(f)=G(f)circ eta _{X}}$ por cada morfismo $f:Xto Y$ . El naturalizador de $eta$ , nat ${displaystyle (eta)}$ , es la subcategoría más grande $C$ que contiene todos los objetos $C$ on which $eta$ restringe a una transformación natural.

Ejemplos

Grupo opuesto

Declaraciones como

"Cada grupo es naturalmente isomorfo a su grupo opuesto"

abundan en matemáticas modernas. Ahora daremos el significado preciso de esta declaración, así como su prueba. Considerar la categoría ${displaystyle {textbf {Grp}}}$ de todos los grupos con homomorfismos de grupo como morfismos. Si $(G, *)$ es un grupo, definimos su grupo opuesto ${displaystyle (G^{text{op}},{*}^{text{op}})}$ como sigue: ${displaystyle G^{text{op}}}$ es el mismo conjunto $G$ , y la operación ${displaystyle *^{text{op}}}$ se define por ${displaystyle a*^{text{op}}b=b*a}$ . Todas las multiplicaciones en ${displaystyle G^{text{op}}}$ son así "volvidos alrededor". Formando el grupo opuesto se convierte un functor (covariante) ${displaystyle {textbf {Grp}}}$ a ${displaystyle {textbf {Grp}}}$ si definimos ${displaystyle f^{text{op}}=f}$ para cualquier homomorfismo de grupo $f:Gto H$ . Note que ${displaystyle f^{text{op}}}$ es un homomorfismo de grupo ${displaystyle G^{text{op}}}$ a ${displaystyle H^{text{op}}}$ :

{displaystyle f^{text{op}}(a*^{text{op}}b)=f(b*a)=f(b)*f(a)=f^{text{op}}(a)*^{text{op}}f^{text{op}}(b).}

El contenido de la declaración anterior es:

"El funerario de identidad

{displaystyle {text{Id}}_{textbf {Grp}}:{textbf {Grp}}to {textbf {Grp}}}

es naturalmente isomorfo al functor opuesto

{displaystyle {text{op}}:{textbf {Grp}}to {textbf {Grp}}}

Para probar esto, necesitamos proporcionar isomorfismos ${displaystyle eta _{G}:Gto G^{text{op}}}$ para cada grupo $G$ , tal que el diagrama anterior conmuta. Set ${displaystyle eta _{G}(a)=a^{-1}}$ . Las fórmulas ${displaystyle (a*b)^{-1}=b^{-1}*a^{-1}=a^{-1}*^{text{op}}b^{-1}}$ y ${displaystyle (a^{-1})^{-1}=a}$ mostrar que ${displaystyle eta _{G}}$ es un grupo homomorfismo con inverso ${displaystyle eta _{G^{text{op}}}}$ . Para probar la naturalidad, comenzamos con un homomorfismo grupo $f:Gto H$ y espectáculo ${displaystyle eta _{H}circ f=f^{text{op}}circ eta _{G}}$ , es decir. ${displaystyle (f(a))^{-1}=f^{text{op}}(a^{-1})}$ para todos $a$ dentro $G$ . Esto es cierto desde entonces ${displaystyle f^{text{op}}=f}$ y cada grupo de homomorfismo tiene la propiedad ${displaystyle (f(a))^{-1}=f(a^{-1})}$ .

Abelianización

Dado un grupo $G$ , podemos definir su abelianización ${displaystyle G^{text{ab}}=G/}$ $[G,G]$ . Vamos ${displaystyle pi _{G}:Gto G^{text{ab}}}$ denota el mapa de proyección en los cosets $[G,G]$ . Este homomorfismo es "natural en $G$ ", es decir, define una transformación natural, que ahora revisamos. Vamos $H$ Sé un grupo. Para cualquier homomorfismo $f:Gto H$ , tenemos eso $[G,G]$ está contenida en el núcleo ${displaystyle pi _{H}circ f}$ , porque cualquier homomorfismo en un grupo abeliano mata al subgrupo del conmutador. Entonces... ${displaystyle pi _{H}circ f}$ factores ${displaystyle G^{text{ab}}}$ como ${displaystyle f^{text{ab}}circ pi _{G}=pi _{H}circ f}$ para el homomorfismo único ${displaystyle f^{text{ab}}:G^{text{ab}}to H^{text{ab}}}$ . Esto hace ${displaystyle {text{ab}}:{textbf {Grp}}to {textbf {Grp}}}$ un functor y $pi$ una transformación natural, pero no un isomorfismo natural, desde el funerario de identidad a ${displaystyle {text{ab}}}$ .

Homomorfismo de Hurewicz

Functores y transformaciones naturales abundan en topología algebraica, con los homomorfismos Hurewicz sirviendo como ejemplos. Para cualquier espacio topológico apuntado ${displaystyle (X,x)}$ y entero positivo $n$ existe un grupo de homomorfismo

{displaystyle h_{*}colon pi _{n}(X,x)to H_{n}(X)}

de la $n$ - el grupo homotopy ${displaystyle (X,x)}$ a la $n$ - grupo de homología $X$ . Ambos $pi _{n}$ y $H_{n}$ son functores de la categoría Top^* de espacios topológicos apuntados a la categoría Grp de grupos, y ${displaystyle h_{*}}$ es una transformación natural $pi _{n}$ a $H_{n}$ .

Determinante

Dados anillos conmutativos $R$ y $S$ con un homomorfismo de anillo $f:Rto S$ , los grupos respectivos de invertibles $ntimes n$ matrices ${displaystyle {text{GL}}_{n}(R)}$ y ${displaystyle {text{GL}}_{n}(S)}$ heredamos un homomorfismo que denotamos ${displaystyle {text{GL}}_{n}(f)}$ , obtenido mediante aplicación $f$ a cada entrada de matriz. Análogamente, $f$ restringe a un homomorfismo grupo ${displaystyle f^{*}:R^{*}to S^{*}}$ , donde $R^{*}$ denota el grupo de unidades $R$ . De hecho, ${displaystyle {text{GL}}_{n}}$ y $*$ son functores de la categoría de anillos conmutativos ${displaystyle {textbf {CRing}}}$ a ${displaystyle {textbf {Grp}}}$ . El determinante del grupo ${displaystyle {text{GL}}_{n}(R)}$ , denotado por ${displaystyle {text{det}}_{R}}$ , es un grupo homomorfismo

{displaystyle {mbox{det}}_{R}colon {mbox{GL}}_{n}(R)to R^{*}}

que es natural en $R$ : porque el determinante se define por la misma fórmula para cada anillo, ${displaystyle fcirc {text{det}}_{R}={text{det}}_{S}circ {text{GL}}_{n}(f)}$ sostiene. Esto hace que el determinante sea una transformación natural ${displaystyle {text{GL}}_{n}}$ a $*$ .

Doble dual de un espacio vectorial

Si $K$ es un campo, entonces para cada espacio vectorial $V$ sobre $K$ tenemos un mapa lineal inyectable "natural" $Vto V^{{**}}$ desde el espacio vectorial en su doble dual. Estos mapas son "naturales" en el siguiente sentido: la doble operación dual es un functor, y los mapas son los componentes de una transformación natural del functor de identidad al doble functor dual.

Cálculo finito

Por cada grupo abeliano $G$ , el conjunto ${displaystyle {text{Hom}}_{textbf {Set}}(mathbb {Z}U(G))}$ of functions from the integers to the underlying set of $G$ forma un grupo abeliano ${displaystyle V_{mathbb {Z} }(G)}$ debajo de la adición de punto. (Aquí) $U$ es el functor olvidadizo estándar ${displaystyle U:{textbf {Ab}}to {textbf {Set}}}$ .) Dado un ${displaystyle {textbf {Ab}}}$ morfismo ${displaystyle varphi:Gto G'}$ , el mapa ${displaystyle V_{mathbb {Z} }(varphi):V_{mathbb {Z} }(G)to V_{mathbb {Z} }(G')}$ dado por la composición izquierda $varphi$ con los elementos de la primera es en sí mismo un homomorfismo de los grupos abelianos; de esta manera obtener un functor ${displaystyle V_{mathbb {Z} }:{textbf {Ab}}to {textbf {Ab}}}$ . El operador de diferencia finita ${displaystyle Delta _{G}}$ tomando cada función ${displaystyle f:mathbb {Z} to U(G)}$ a ${displaystyle Delta (f):nmapsto f(n+1)-f(n)}$ es un mapa de ${displaystyle V_{mathbb {Z} }(G)}$ a sí mismo, y la colección $Delta$ de tales mapas da una transformación natural ${displaystyle Delta:V_{mathbb {Z} }to V_{mathbb {Z} }}$ .

Adjunción tensor-hom

Considerar el categoría ${displaystyle {textbf {Ab}}}$ de grupos abelianos y homomorfismos de grupo. Para todos los grupos abelianos $X$ , $Y$ y $Z$ tenemos un isomorfismo grupo

{displaystyle {text{Hom}}(Xotimes Y,Z)to {text{Hom}}(X,{text{Hom}}(Y,Z))}

Estos isomorfismos son "naturales" en el sentido de que definen una transformación natural entre los dos funerarios involucrados ${displaystyle {textbf {Ab}}^{text{op}}times {textbf {Ab}}^{text{op}}times {textbf {Ab}}to {textbf {Ab}}}$ . (Aquí "op" es la categoría opuesta de ${displaystyle {textbf {Ab}}}$ , para no confundirse con el trivial functor de grupo opuesto en ${displaystyle {textbf {Ab}}}$ !

Esta es formalmente la adjunción tensor-hom y es un ejemplo arquetípico de un par de funtores adjuntos. Las transformaciones naturales surgen con frecuencia junto con los funtores adjuntos y, de hecho, los funtores adjuntos se definen por un cierto isomorfismo natural. Además, cada par de funtores adjuntos viene equipado con dos transformaciones naturales (generalmente no isomorfismos) llamadas unidad y counidad.

Isomorfismo no natural

La noción de una transformación natural es categórica, y afirma (informativamente) que un mapa particular entre los funerarios se puede hacer consistentemente sobre toda una categoría. Informalmente, un mapa particular (esp. un isomorfismo) entre objetos individuales (no categorías enteras) se conoce como un " isomorfismo natural", que significa implícitamente que se define en toda la categoría, y define una transformación natural de los funerarios; formalizar esta intuición fue un factor motivador en el desarrollo de la teoría de la categoría. Por el contrario, se puede llamar un mapa particular entre objetos particulares isomorfismo antinatural (o "este isomorfismo no es natural") si el mapa no puede extenderse a una transformación natural en toda la categoría. Dado un objeto $X,$ un functor $G$ (tomar la simplicidad al primer functor como identidad) y un isomorfismo $etacolon X to G(X),$ prueba de la antinaturalidad se muestra más fácilmente dando un automorfismo $Acolon X to X$ que no se comunica con este isomorfismo (también $eta circ A neq G(A) circ eta$ ). Más fuerte, si uno desea probar que $X$ y ${displaystyle G(X)}$ no son naturalmente isomorfos, sin referencia a un isomorfismo particular, esto requiere mostrar que para cualquiera isomorfismo $eta$ , hay algunos $A$ con el que no se comunica; en algunos casos un solo automorfismo $A$ trabaja para todos los isomorfismos candidatos $eta$ mientras que en otros casos uno debe mostrar cómo construir un diferente ${displaystyle A_{eta }}$ para cada isomorfismo. Los mapas de la categoría juegan un papel crucial: cualquier transformación infranatural es natural si los únicos mapas son el mapa de identidad, por ejemplo.

Esto es similar (pero más categórico) a los conceptos de la teoría de grupos o la teoría de módulos, donde una descomposición dada de un objeto en una suma directa "no es natural", o más bien "no es única". #34;, ya que existen automorfismos que no conservan la descomposición de la suma directa; consulte el teorema de estructura para módulos generados finitamente sobre un dominio ideal principal § Uniqueness, por ejemplo.

Algunos autores distinguen notacionalmente, utilizando $cong$ para un isomorfismo natural y $approx$ para un isomorfismo antinatural, reservando ${displaystyle =}$ para la igualdad (por lo general igualdad de mapas).

Ejemplo: grupo fundamental de toroide

Como ejemplo de la distinción entre el enunciado funcional y los objetos individuales, considere los grupos de homotopía de un espacio producto, específicamente el grupo fundamental del toro.

Los grupos de homotopy de un espacio de producto son naturalmente el producto de los grupos de homotopy de los componentes, $pi_n((X,x_0) times (Y,y_0)) cong pi_n((X,x_0)) times pi_n((Y,y_0)),$ con el isomorfismo dado por proyección sobre los dos factores, fundamentalmente porque los mapas en un espacio de productos son exactamente productos de mapas en los componentes – esta es una declaración functorial.

Sin embargo, el toro (que es abstractamente un producto de dos círculos) tiene un grupo fundamental isomorfo a $Z^{2}$ , pero la división $pi_1(T,t_0) approx mathbf{Z} times mathbf{Z}$ no es natural. Note el uso de $approx$ , $cong$ , y $=$ :

pi_1(T,t_0) approx pi_1(S^1,x_0) times pi_1(S^1,y_0) cong mathbf{Z} times mathbf{Z} = mathbf{Z}^2.

Este isomorfismo abstracto con un producto no es natural, como algunos isomorfismos de $T$ no preservar el producto: el auto-homeomorfismo $T$ (pensado como el espacio de referencia ${displaystyle R^{2}/mathbb {Z} ^{2}}$ ) dado por $left(begin{smallmatrix}1 & 1\0 & 1end{smallmatrix}right)$ (geométricamente un giro de Dehn sobre una de las curvas generadoras) actúa como esta matriz en $mathbb {Z} ^{2}$ (está en el grupo lineal general ${displaystyle {text{GL}}(mathbb {Z}2)}$ de matrices enteros invertibles), que no preserva la descomposición como producto porque no es diagonal. Sin embargo, si se le da el toro como producto $(T,t_0) = (S^1,x_0) times (S^1,y_0)$ – equivalentemente, dada una descomposición del espacio – entonces la división del grupo sigue de la declaración general anterior. En términos categóricos, la categoría relevante (preservando la estructura de un espacio de producto) es "mapas de espacios de productos, a saber, un par de mapas entre los componentes respectivos".

La naturalidad es una noción categórica y requiere ser muy preciso acerca de qué datos exactamente se dan: el toroide como un espacio que resulta ser un producto (en la categoría de espacios y mapas continuos) es diferente del toroide presentado como un producto (en la categoría de productos de dos espacios y mapas continuos entre los respectivos componentes).

Ejemplo: dual de un espacio vectorial de dimensión finita

Todo espacio vectorial de dimensión finita es isomorfo a su espacio dual, pero puede haber muchos isomorfismos diferentes entre los dos espacios. En general, no existe un isomorfismo natural entre un espacio vectorial de dimensión finita y su espacio dual. Sin embargo, las categorías relacionadas (con estructura adicional y restricciones en los mapas) tienen un isomorfismo natural, como se describe a continuación.

El espacio dual de un espacio vectorial de dimensión finita es de nuevo un espacio vectorial de dimensión finita de la misma dimensión y, por lo tanto, son isomorfos, ya que la dimensión es la única invariante de los espacios vectoriales de dimensión finita en un campo dado. Sin embargo, en ausencia de restricciones adicionales (como el requisito de que los mapas conserven la base elegida), el mapa de un espacio a su dual no es único y, por lo tanto, tal isomorfismo requiere una elección y "no es natural& #34;. En la categoría de espacios vectoriales de dimensión finita y mapas lineales, se puede definir un isomorfismo infranatural de espacios vectoriales a su dual eligiendo un isomorfismo para cada espacio (digamos, eligiendo una base para cada espacio vectorial y tomando el isomorfismo correspondiente), pero esto no definirá una transformación natural. Intuitivamente esto se debe a que requiere una elección, rigurosamente porque cualquier elección de isomorfismos no conmutará con, digamos, el mapa cero; ver (Mac Lane & Birkhoff 1999, §VI.4) para una discusión detallada.

Partiendo de espacios vectoriales de dimensiones finitas (como objetos) y de la identidad y de los duales functores, se puede definir un isomorfismo natural, pero esto requiere primero añadir estructura adicional, luego restringir los mapas de "todos los mapas lineales" a "mapas lineales que respetan esta estructura". Explícitamente, para cada espacio vectorial, requieren que viene con los datos de un isomorfismo a su dual, $eta_Vcolon V to V^*$ . En otras palabras, tomar como objetos espacios vectoriales con una forma bilineal nodegenerada $b_Vcolon V times V to K$ . Esto define un isomorfismo infranatural (isomorfismo para cada objeto). Una entonces restringe los mapas a sólo esos mapas ${displaystyle Tcolon Vto U}$ que se comunica con los isomorfismos: ${displaystyle T^{*}(eta _{U}(T(v)))=eta _{V}(v)}$ o en otras palabras, preservar la forma bilineal: ${displaystyle b_{U}(T(v),T(w))=b_{V}(v,w)}$ . (Estos mapas definen el naturalizador de los isomorfismos.) La categoría resultante, con objetos espacios vectoriales finitos con forma bilineal nondegenerada, y mapas transformaciones lineales que respetan la forma bilineal, por construcción tiene un isomorfismo natural de la identidad a la dual (cada espacio tiene un isomorfismo a su dual, y los mapas de la categoría son necesarios para conmutar). Visto en esta luz, esta construcción (add transforma para cada objeto, restringe los mapas para comulgar con ellos) es completamente general, y no depende de ninguna propiedad particular de los espacios vectoriales.

En esta categoría (espacios vectoriales de dimensión finita con una forma bilineal no degenerada, mapas transformados lineales que respetan la forma bilineal), el dual de un mapa entre espacios vectoriales puede identificarse como una transposición. A menudo, por razones de interés geométrico, esto se especializa en una subcategoría, al requerir que las formas bilineales no degeneradas tengan propiedades adicionales, como ser simétricas (matrices ortogonales), simétricas y definidas positivas (espacio de producto interno), simétricas sesquilineales (espacios hermitianos), sesgado-simétrico y totalmente isótropo (espacio vectorial simpléctico), etc. – en todas estas categorías un espacio vectorial se identifica naturalmente con su dual, por la forma bilineal no degenerada.

Operaciones con transformaciones naturales

Composición horizontal y vertical de las transformaciones naturales

Composición vertical

Si ${displaystyle eta:FRightarrow G}$ y ${displaystyle epsilon:GRightarrow H}$ son transformaciones naturales entre functores ${displaystyle F,G,H:Cto D}$ , entonces podemos componerlos para conseguir una transformación natural ${displaystyle epsilon circ eta:FRightarrow H}$ . Esto se hace a partir de componentes:

{displaystyle (epsilon circ eta)_{X}=epsilon _{X}circ eta _{X}}

Esta composición vertical de transformaciones naturales es asociativa y tiene una identidad, y permite considerar la colección de todos los funerarios $C to D$ como categoría (ver abajo en las categorías de Functor). La identidad transformación natural ${displaystyle mathrm {id} _{F}}$ en functor $F$ tiene componentes ${displaystyle (mathrm {id} _{F})_{X}=mathrm {id} _{F(X)}}$ .

Para

{displaystyle eta:FRightarrow G}

{displaystyle mathrm {id} _{G}circ eta =eta =eta circ mathrm {id} _{F}}

Composición horizontal

Si ${displaystyle eta:FRightarrow G}$ es una transformación natural entre hongos ${displaystyle F,G:Cto D}$ y ${displaystyle epsilon:JRightarrow K}$ es una transformación natural entre hongos ${displaystyle J,K:Dto E}$ , entonces la composición de los funerarios permite una composición de transformaciones naturales ${displaystyle epsilon *eta:Jcirc FRightarrow Kcirc G}$ con componentes

{displaystyle (epsilon *eta)_{X}=epsilon _{G(X)}circ J(eta _{X})=K(eta _{X})circ epsilon _{F(X)}}

Usando bigotes (ver abajo), podemos escribir

{displaystyle (epsilon *eta)_{X}=(epsilon G)_{X}circ (Jeta)_{X}=(Keta)_{X}circ (epsilon F)_{X}}

por lo tanto

{displaystyle epsilon *eta =epsilon Gcirc Jeta =Keta circ epsilon F}

Esta composición horizontal de las transformaciones naturales también está asociada a la identidad. Esta identidad es la transformación natural de identidad en el functor de identidad, es decir, la transformación natural que asocia a cada objeto su morfismo de identidad: para el objeto $X$ en la categoría $C$ , ${displaystyle (mathrm {id} _{mathrm {id} _{C}})_{X}=mathrm {id} _{mathrm {id} _{C}(X)}=mathrm {id} _{X}}$ .

Para

{displaystyle eta:FRightarrow G}

con

{displaystyle F,G:Cto D}

{displaystyle mathrm {id} _{mathrm {id} _{D}}*eta =eta =eta *mathrm {id} _{mathrm {id} _{C}}}

Como functores de identidad ${displaystyle mathrm {id} _{C}}$ y ${displaystyle mathrm {id} _{D}}$ son functores, la identidad para la composición horizontal es también la identidad para la composición vertical, pero no viceversa.

Bigotes

Whiskering es una operación binaria externa entre un funtor y una transformación natural.

Si ${displaystyle eta:FRightarrow G}$ es una transformación natural entre hongos ${displaystyle F,G:Cto D}$ , y ${displaystyle H:Dto E}$ es otro functor, entonces podemos formar la transformación natural ${displaystyle Heta:Hcirc FRightarrow Hcirc G}$ definiendo

{displaystyle (Heta)_{X}=H(eta _{X})}

Si en cambio ${displaystyle K:Bto C}$ es un functor, la transformación natural ${displaystyle eta K:Fcirc KRightarrow Gcirc K}$ se define por

{displaystyle (eta K)_{X}=eta _{K(X)}}

También es una composición horizontal donde una de las transformaciones naturales es la transformación natural de la identidad:

{displaystyle Heta =mathrm {id} _{H}*eta }

{displaystyle eta K=eta *mathrm {id} _{K}}

Note que ${displaystyle mathrm {id} _{H}}$ (Resp. ${displaystyle mathrm {id} _{K}}$ ) generalmente no es la identidad izquierda (resp. derecha) de la composición horizontal $*$ () ${displaystyle Heta neq eta }$ y ${displaystyle eta Kneq eta }$ en general), excepto si $H$ (Resp. $K$ ) es el functor de identidad de la categoría $D$ (Resp. $C$ ).

Ley de intercambio

Las dos operaciones están relacionadas con una identidad que intercambia composición vertical con composición horizontal: si tenemos cuatro transformaciones naturales ${displaystyle alphaalpha ',betabeta '}$ como se muestra en la imagen a la derecha, entonces la siguiente identidad sostiene:

{displaystyle (beta 'circ alpha ')*(beta circ alpha)=(beta '*beta)circ (alpha '*alpha)}

Las composiciones verticales y horizontales también están vinculadas a través de transformaciones naturales de identidad:

para

F:Cto D

{displaystyle G:Dto E}

{displaystyle mathrm {id} _{G}*mathrm {id} _{F}=mathrm {id} _{Gcirc F}}

Como el silbido es la composición horizontal con una identidad, la ley de intercambio da inmediatamente las fórmulas compactas de la composición horizontal de ${displaystyle eta:FRightarrow G}$ y ${displaystyle epsilon:JRightarrow K}$ sin tener que analizar los componentes y el diagrama conmutativo:

{displaystyle {begin{aligned}epsilon *eta &=(epsilon circ mathrm {id} _{J})*(mathrm {id} _{G}circ eta)=(epsilon *mathrm {id} _{G})circ (mathrm {id} _{J}*eta)=epsilon Gcirc Jeta \&=(mathrm {id} _{K}circ epsilon)*(eta circ mathrm {id} _{F})=(mathrm {id} _{K}*eta)circ (epsilon *mathrm {id} _{F})=Keta circ epsilon Fend{aligned}}}

Categorías de funtores

Si $C$ es cualquier categoría y $I$ es una pequeña categoría, podemos formar la categoría de functor $C^I$ tener como objetos todos los functores de $I$ a $C$ y como morfismos las transformaciones naturales entre esos functores. Esta forma una categoría desde para cualquier functor $F$ hay una transformación natural de identidad ${displaystyle 1_{F}:Fto F}$ (que asigna a cada objeto $X$ el morfismo de identidad en $F(X)$ ) y la composición de dos transformaciones naturales (la "composición vertical" arriba) es otra vez una transformación natural.

Los isomorfismos en $C^I$ son precisamente los isomorfismos naturales. Es decir, una transformación natural $eta: F to G$ es un isomorfismo natural si existe una transformación natural $epsilon: G to F$ tales que ${displaystyle eta epsilon =1_{G}}$ y ${displaystyle epsilon eta =1_{F}}$ .

La categoría de functor $C^I$ es especialmente útil si $I$ surge de un gráfico dirigido. Por ejemplo, si $I$ es la categoría del gráfico dirigido • →, entonces $C^I$ tiene como objetos los morfismos de $C$ , y un morfismo entre ${displaystyle phi:Uto V}$ y ${displaystyle psi:Xto Y}$ dentro $C^I$ es un par de morfismos $f: U to X$ y ${displaystyle g:Vto Y}$ dentro $C$ tal que los "square commutes", es decir. ${displaystyle psi circ f=gcirc phi }$ .

Más generalmente, se puede construir la 2-categoría ${displaystyle {textbf {Cat}}}$ cuyo

0-células (objetos) son las pequeñas categorías,
1-células (flechas) entre dos objetos $C$ y $D$ son los funerarios de $C$ a $D$ ,
2 celdas entre dos 1 celdas (functores) $F:Cto D$ y $G:Cto D$ son las transformaciones naturales de $F$ a $G$ .

Las composiciones horizontales y verticales son las composiciones entre transformaciones naturales descritas anteriormente. Una categoría de functor $C^I$ es entonces simplemente una hom-categoría en esta categoría (smallness emite aparte).

Más ejemplos

Cada límite y colímite proporciona un ejemplo de una transformación natural simple, ya que un cono equivale a una transformación natural con el funtor diagonal como dominio. De hecho, si los límites y los colímites se definen directamente en términos de su propiedad universal, son morfismos universales en una categoría de funtores.

Lema de Yoneda

Si $X$ es un objeto de una categoría localmente pequeña $C$ , entonces la asignación ${displaystyle Ymapsto {text{Hom}}_{C}(X,Y)}$ define un functor covariante ${displaystyle F_{X}:Cto {textbf {Set}}}$ . Este functor se llama representable (más generalmente, un functor representable es cualquier functor naturalmente isomorfo para este functor para una elección adecuada $X$ ). Las transformaciones naturales de un functor representable a un functor arbitrario ${displaystyle F:Cto {textbf {Set}}}$ son completamente conocidos y fáciles de describir; este es el contenido de la lemma Yoneda.

Notas históricas

Se dice que Saunders Mac Lane, uno de los fundadores de la teoría de categorías, comentó: "Yo no inventé las categorías para estudiar los funtores; Los inventé para estudiar las transformaciones naturales." Así como el estudio de los grupos no está completo sin el estudio de los homomorfismos, el estudio de las categorías no está completo sin el estudio de los funtores. La razón del comentario de Mac Lane es que el estudio de los funtores en sí mismo no está completo sin el estudio de las transformaciones naturales.

El contexto del comentario de Mac Lane fue la teoría axiomática de la homología. Se podría demostrar que coinciden diferentes formas de construir la homología: por ejemplo, en el caso de un complejo simplicial, los grupos definidos directamente serían isomorfos a los de la teoría singular. Lo que no se puede expresar fácilmente sin el lenguaje de las transformaciones naturales es cómo los grupos de homología son compatibles con los morfismos entre objetos, y cómo dos teorías de homología equivalentes no solo tienen los mismos grupos de homología, sino también los mismos morfismos entre esos grupos.

Contenido relacionado

Más resultados...