Transformación activa y pasiva

En geometría analítica, transformaciones espaciales en el espacio euclidiano tridimensional R3{displaystyle mathbb {R} {} {}}} se distinguen en activo o transformaciones de coartada, y pasivo o entre otras transformaciones. An transformación activa es una transformación que realmente cambia la posición física (alibi, en otros lugares) de un punto, o cuerpo rígido, que se puede definir en ausencia de un sistema de coordenadas; mientras que un transformación pasiva es simplemente un cambio en el sistema de coordenadas en el que se describe el objeto (alias, otro nombre) (cambio de mapa de coordenadas, o cambio de base). Por transformación, los matemáticos generalmente se refieren a transformaciones activas, mientras que los físicos e ingenieros podrían significar tampoco. Ambos tipos de transformación pueden ser representados por una combinación de una traducción y una transformación lineal.

Dicho de otra manera, una transformación pasiva se refiere a la descripción del mismo objeto en dos sistemas de coordenadas diferentes. Por otro lado, una transformación activa es una transformación de uno o más objetos con respecto al mismo sistema de coordenadas. Por ejemplo, las transformaciones activas son útiles para describir posiciones sucesivas de un cuerpo rígido. Por otro lado, las transformaciones pasivas pueden ser útiles en el análisis del movimiento humano para observar el movimiento de la tibia con respecto al fémur, es decir, su movimiento con respecto a un sistema de coordenadas (local) que se mueve junto con el fémur, en lugar de un sistema de coordenadas (global) fijado al suelo.

Ejemplo

Como ejemplo, deja que el vector v=()v1,v2)▪ ▪ R2{displaystyle mathbf {v} =(v_{1},v_{2})in mathbb {R} ^{2}Sé un vector en el avión. Una rotación del vector a través de un ángulo Silencio en dirección en sentido contrario se da por la matriz de rotación:

R=()#⁡ ⁡ Silencio Silencio − − pecado⁡ ⁡ Silencio Silencio pecado⁡ ⁡ Silencio Silencio #⁡ ⁡ Silencio Silencio ),{displaystyle R={begin{pmatrix}cos theta &-sin theta \sin theta &cos theta end{pmatrix}}}}

Transformaciones espaciales en el espacio euclidiano R3

En general una transformación espacial T:: R3→ → R3{displaystyle Tcolon mathbb {R} ^{3}to mathbb {R} ^{3} puede consistir en una traducción y una transformación lineal. En lo siguiente, se omitirá la traducción, y la transformación lineal estará representada por una matriz 3×3 T{displaystyle T}.

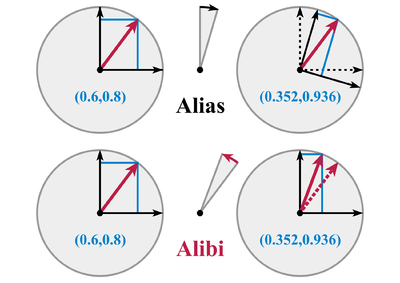
Transformación activa

Como transformación activa, T{displaystyle T} transforma el vector inicial v=()vx,vSí.,vz){displaystyle mathbf {v} =(v_{x},v_{y},v_{z}) } en un nuevo vector v.=()vx.,vSí..,vz.)=Tv=T()vx,vSí.,vz){displaystyle mathbf {v} '=(v'_{x},v'_{y},v'_{z})=Tmathbf {v} =T(v_{x},v_{y},v_{z})}}.

Si hay una vista {}ex.=T()1,0,0),eSí..=T()0,1,0),ez.=T()0,0,1)}{displaystyle {mathbf {e} '_{x}=T(1,0,0),mathbf {e} '_{y}=T(0,1,0),mathbf {e}=T(0,0,1)}}} como nueva base, entonces las coordenadas del nuevo vector v.=vxex.+vSí.eSí..+vzez.{displaystyle mathbf {v} '=v_{x}mathbf {e} "Mathbf" ¿Qué? en la nueva base son los mismos v=vxex+vSí.eSí.+vzez{displaystyle mathbf {v} =v_{x}mathbf {e} ¿Qué? ¿Qué? en la base original. Tenga en cuenta que las transformaciones activas tienen sentido incluso como una transformación lineal en un espacio vectorial diferente. Tiene sentido escribir el nuevo vector en la base desenfrenada (como arriba) sólo cuando la transformación es del espacio en sí misma.

Transformación pasiva

Por otro lado, cuando uno mira T{displaystyle T} como una transformación pasiva, el vector inicial v=()vx,vSí.,vz){displaystyle mathbf {v} =(v_{x},v_{y},v_{z}) } se deja sin cambios, mientras que el sistema de coordenadas y sus vectores de base se transforman en la dirección opuesta, es decir, con la transformación inversa T− − 1{displaystyle T^{-1}. Esto da un nuevo sistema de coordenadas XYZ con vectores de base:

eX=T− − 1()1,0,0),eY=T− − 1()0,1,0),eZ=T− − 1()0,0,1){displaystyle mathbf {e} ¿Por qué? ¿Qué? ¿Qué?

Las nuevas coordenadas ()vX,vY,vZ){displaystyle (v_{X},v_{Y},v_{Z}} de v{displaystyle mathbf {v} con respecto al nuevo sistema de coordinación XYZ son dados por:

v=()vx,vSí.,vz)=vXeX+vYeY+vZeZ=T− − 1()vX,vY,vZ).{displaystyle mathbf {v} =(v_{x},v_{y},v_{z})=v_{X}e_{X}+v_{Y}e_{Y}e_{Z}=T^{-1}(v_{X},v_{Y},v_{Z}}}}}

De esta ecuación se ve que las nuevas coordenadas están dadas por

()vX,vY,vZ)=T()vx,vSí.,vz).{displaystyle (v_{X},v_{Y},v_{Z})=T(v_{x},v_{y},v_{z}).}

Como transformación pasiva T{displaystyle T} transforma las antiguas coordenadas en las nuevas.

Tenga en cuenta la equivalencia entre los dos tipos de transformaciones: las coordenadas del nuevo punto en la transformación activa y las nuevas coordenadas del punto en la transformación pasiva son las mismas, es decir

()vX,vY,vZ)=()vx.,vSí..,vz.).{displaystyle (v_{X},v_{Y},v_{Z}=(v'_{x},v'_{y},v'_{z}).}

En espacios vectoriales abstractos

La distinción entre transformaciones activas y pasivas se puede ver matemáticamente considerando espacios vectoriales abstractos.

Fijar un espacio vectorial de dimensiones finitas V{displaystyle V} sobre un terreno K{displaystyle K} (pensamiento de como R{displaystyle mathbb {R} o C{displaystyle mathbb {C}), y una base B={}ei}1≤ ≤ i≤ ≤ n{fnMicrosoft} {fnK}\fnh}\fnh}\fnK}\fn}\fnK}\\fn}\\fn}\\fn}\\fnK}\\\fnK}\fnK}}\\\\fnK}}}}\\\\fn}\\\\fn}\\\\\fn}\\\\\\\fn}\\fn}\\\\\\fn}\fnh}}\\\\\\\\fnh}}\\\\\\\\\\\cH}}\\\\\\ ileq n} de V{displaystyle V}. Esta base proporciona un isomorfismo C:Kn→ → V{displaystyle C:K^{n}rightarrow V. a través del mapa del componente ()vi)1≤ ≤ i≤ ≤ n=()v1,⋯ ⋯ ,vn)↦ ↦ .. iviei{textstyle (v_{i})_{1leq ileq n}=(v_{1},cdotsv_{n})mapsto sum ¿Qué?.

An transformación activa es entonces un endomorfismo en V{displaystyle V}, es decir, un mapa lineal V{displaystyle V} a sí mismo. Tomar tal transformación τ τ ▪ ▪ Final()V){displaystyle tau in {text{End}(V)}, un vector v▪ ▪ V{displaystyle vin V} transforma como v↦ ↦ τ τ v{displaystyle vmapsto tau v}. Los componentes τ τ {displaystyle tau } con respecto a la base B{displaystyle {máthcal {B}} se definen a través de la ecuación τ τ ei=.. jτ τ jiej{textstyle tau E_{i}=sum _{j}tau _{ji}e_{j}. Luego, los componentes de v{displaystyle v} transformada vi↦ ↦ τ τ ijvj{displaystyle v_{i}mapsto tau _{ij}v_{j}}.

A transformación pasiva es en cambio un endomorfismo Kn{displaystyle K^{n}. Esto se aplica a los componentes: vi↦ ↦ Tijvj=vi.{displaystyle v_{i}mapsto T_{ij}v_{j}=:v'_{i}. La nueva base B.={}ei.}{fnMicrosoft} {fnK} {fnK}}} {fnK}}} {fnK}}} se determina pidiendo que viei=vi.ei.{displaystyle ¿Qué?, de la cual la expresión ei.=()T− − 1)jiej{displaystyle ¿Qué? puede ser derivado.

Aunque los espacios Final()V){displaystyle {text{End}(V)} y Final()Kn){displaystyle {text{End}}({K^{n}) } son isomorfos, no son canónicamente isomorfos. Sin embargo, una elección de la base B{displaystyle {máthcal {B}} permite la construcción de un isomorfismo.

Como acciones de izquierda y derecha

A menudo se limita al caso en que los mapas son invertibles, de modo que las transformaciones activas son el grupo lineal general GL()V){displaystyle {text{GL}(V)} de transformaciones mientras las transformaciones pasivas son el grupo GL()n,K){displaystyle {text{GL}(n,K)}.

Las transformaciones pueden entonces entenderse como actuar en el espacio de bases para V{displaystyle V}. Una transformación activa τ τ ▪ ▪ GL()V){displaystyle tau in {text{GL}(V)} envía la base {}ei}↦ ↦ {}τ τ ei}{displaystyle "Mapsto" {fn}. Mientras tanto, una transformación pasiva T▪ ▪ GL()n,K){displaystyle Tin {text{GL}(n,K)} envía la base {}ei}↦ ↦ {}.. j()T− − 1)jiej}{textstyle {e_{i}mapsto left{sum ¿Qué?.

El inverso en la transformación pasiva garantiza el componentes transformados idénticos τ τ {displaystyle tau } y T{displaystyle T}. Esto da una distinción aguda entre transformaciones activas y pasivas: las transformaciones activas actúan desde la izquierda en bases, mientras que las transformaciones pasivas actúan desde la derecha, debido a la inversa.

Esta observación se hace más natural al ver bases B{displaystyle {máthcal {B}} como una elección del isomorfismo CCPR CCPR B:V→ → Kn{displaystyle Phi _{mathcal {B}:Vrightarrow K^{n}. El espacio de bases es equivalentemente el espacio de tales isomorfismos, denotados Iso()V,Kn){displaystyle {text{Iso}(V,K^{n}}. Transformaciones activas, identificadas con GL()V){displaystyle {text{GL}(V)}, actuar en Iso()V,Kn){displaystyle {text{Iso}(V,K^{n}} de la izquierda por composición, mientras transformaciones pasivas, identificadas con GL()n,K){displaystyle {text{GL}(n,K)} actos Iso()V,Kn){displaystyle {text{Iso}(V,K^{n}} de la derecha por pre-composición.

Esto convierte el espacio de bases en un izquierda GL()V){displaystyle {text{GL}(V)}-torredor y un derecho GL()n,K){displaystyle {text{GL}(n,K)}- Señor.

Desde una perspectiva física, las transformaciones activas se pueden caracterizar como transformaciones del espacio físico, mientras que las transformaciones pasivas se caracterizan como redundancias en la descripción del espacio físico. Esto juega un papel importante en la teoría matemática de calibre, donde las transformaciones de calibre se describen matemáticamente mediante mapas de transición que actúan desde la derecha sobre las fibras.