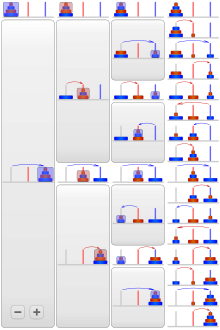
Torre de Hanoi

Un modelo de la Torre de Hanoi (con 8 discos)

Una solución animada de la Torre de Hanoi rompecabezas para T(4, 3)

Torre de la exposición interactiva Hanoi en el Museo Universum de la Ciudad de México

La Torre de Hanoi (también llamada El problema del Templo de Benarés o Torre de Brahma o Torre de Lucas'< /b> y a veces pluralizado como Torres, o simplemente rompecabezas piramidal) es un juego o rompecabezas matemático que consta de tres varillas y una serie de discos de varios diámetros, que pueden deslizarse sobre cualquier varilla. El rompecabezas comienza con los discos apilados en una barra en orden decreciente de tamaño, el más pequeño en la parte superior, acercándose así a una forma cónica. El objetivo del rompecabezas es mover toda la pila hasta la última barra, obedeciendo las siguientes reglas:

1. Sólo un disco se puede mover a la vez.
2. Cada movimiento consiste en tomar el disco superior de una de las pilas y colocarlo en la parte superior de otra pila o en una varilla vacía.
3. Ningún disco se puede colocar en la parte superior de un disco que es más pequeño que él.

Con 3 discos, el rompecabezas se puede resolver en 7 movimientos. El número mínimo de movimientos necesarios para resolver un rompecabezas de la Torre de Hanoi es 2ⁿ − 1, donde n es el número de discos.

Orígenes

El acertijo fue introducido en Occidente por el matemático francés Édouard Lucas en 1883. Numerosos mitos sobre la naturaleza antigua y mística del acertijo surgieron casi de inmediato, incluido uno sobre un templo indio en Kashi Vishwanath que contiene una gran sala con tres postes desgastados por el tiempo, rodeados por 64 discos dorados. Siguiendo el mandato de una antigua profecía, los sacerdotes brahmanes han estado moviendo estos discos de acuerdo con las reglas inmutables de Brahma desde ese momento. Por lo tanto, el rompecabezas también se conoce como la Torre de Brahma. Según la leyenda, cuando se complete el último movimiento del rompecabezas, el mundo terminará.

Si la leyenda fuera cierta, y si los sacerdotes fueran capaces de mover discos a razón de uno por segundo, usando el menor número de movimientos, les tomaría 2⁶⁴ − 1 segundo o aproximadamente 585 mil millones de años para terminar, que es aproximadamente 42 veces la edad actual del universo.

Hay muchas variaciones de esta leyenda. Por ejemplo, en algunos relatos, el templo es un monasterio y los sacerdotes son monjes. El templo o monasterio puede estar en varios lugares, incluido Hanoi, y puede estar asociado con cualquier religión. En algunas versiones se introducen otros elementos, como el hecho de que la torre se creó al principio del mundo, o que los sacerdotes o monjes sólo pueden realizar un movimiento al día.

Solución

El rompecabezas se puede jugar con cualquier número de discos, aunque muchas versiones de juguete tienen alrededor de 7 a 9 de ellos. El número mínimo de movimientos necesarios para resolver un rompecabezas de la Torre de Hanoi es 2ⁿ − 1, donde n es el número de discos.

Solución iterativa

Animación de un algoritmo iterativo que resolver 6-disk problema

Una solución simple para el rompecabezas de juguete es alternar movimientos entre la pieza más pequeña y una pieza no más pequeña. Cuando mueva la pieza más pequeña, muévala siempre a la siguiente posición en la misma dirección (hacia la derecha si el número inicial de piezas es par, hacia la izquierda si el número inicial de piezas es impar). Si no hay una posición de torre en la dirección elegida, mueva la pieza al extremo opuesto, pero luego continúe moviéndose en la dirección correcta. Por ejemplo, si comenzó con tres piezas, movería la pieza más pequeña al extremo opuesto y luego continuaría en la dirección izquierda después de eso. Cuando el turno es mover la pieza que no es la más pequeña, solo hay un movimiento legal. Hacer esto completará el rompecabezas en la menor cantidad de movimientos.

Declaración más simple de solución iterativa

Para un número par de discos:

• hacer el movimiento legal entre las pelucas A y B (en cualquier dirección),
• hacer el movimiento legal entre las pelucas A y C (en cualquier dirección),
• hacer el movimiento legal entre los pegs B y C (en cualquier dirección),
• repetir hasta completar.

Para un número impar de discos:

• hacer el movimiento legal entre las pelucas A y C (en cualquier dirección),
• hacer el movimiento legal entre las pelucas A y B (en cualquier dirección),
• hacer el movimiento legal entre los pegs B y C (en cualquier dirección),
• repetir hasta completar.

En cada caso, se realizan un total de 2ⁿ − 1 movimientos.

Solución iterativa equivalente

Otra forma de generar la solución iterativa óptima única:

Numera los discos del 1 al n (de mayor a menor).

• Si n es extraño, el primer movimiento es de peluca A a peluca C.
• Si n es incluso, el primer movimiento es de la peluca A a la peluca B.

Ahora, agregue estas restricciones:

• Ningún disco extraño puede ser colocado directamente en un disco extraño.
• Ni siquiera el disco se puede colocar directamente en un disco.
• A veces habrá dos pelucas posibles: una tendrá discos, y la otra estará vacía. Coloque el disco en la peluca no vacía.
• Nunca mueva un disco dos veces en sucesión.

Considerando esas restricciones después del primer movimiento, solo hay un movimiento legal en cada turno subsiguiente.

La secuencia de estos movimientos únicos es una solución óptima al problema equivalente a la solución iterativa descrita anteriormente.

Solución recursiva

Ilustración de una solución recursiva para el rompecabezas Towers of Hanoi con 4 discos. En el archivo SVG, haga clic en un botón gris para expandirlo o colapsarlo

La clave para resolver un problema recursivamente es reconocer que se puede dividir en una colección de subproblemas más pequeños, a cada uno de los cuales se aplica el mismo procedimiento general de resolución que buscamos, y la solución total se encuentra de alguna manera simple a partir de esos subproblemas' soluciones Cada uno de estos subproblemas creados es "más pequeño" garantiza que eventualmente se alcanzarán los casos base. Desde allí, para las Torres de Hanoi:

• etiqueta las pelucas A, B, C,
• Deja n ser el número total de discos,
• numerar los discos de 1 (smallest, topmos) a n (más grande, más abajo).

Suponiendo que todos los n discos se distribuyen en arreglos válidos entre las clavijas; suponiendo que hay m discos superiores en una clavija de origen, y que el resto de los discos son más grandes que m, por lo que pueden ignorarse con seguridad; para mover m discos de una clavija de origen a una clavija de destino utilizando una clavija de repuesto, sin infringir las reglas:

1. Muévanse. m − 1 discos de los fuente a la repuesto Peg, por el mismo procedimiento de resolución general. Las reglas no se violan, por supuesto. Esto deja el disco m como un disco superior en la peluca fuente.
2. Mover el disco m de la fuente a la objetivo peg, que está garantizada a ser un movimiento válido, por los supuestos — un simple paso.
3. Muévete. m − 1 discos que acabamos de colocar en el repuesto, desde el repuesto a la objetivo Peg by el mismo procedimiento de resolución general, por lo que se colocan en la parte superior del disco m sin violar las reglas.
4. El caso base es moverse 0 discos (en los pasos 1 y 3), es decir, no hagan nada – que obviamente no viola las reglas.

La solución completa de la Torre de Hanoi consiste en mover n discos desde la clavija de origen A a la clavija de destino C, utilizando B como clavija de repuesto.

A este enfoque se le puede dar una prueba matemática rigurosa con inducción matemática y, a menudo, se usa como ejemplo de recursividad cuando se enseña programación.

Análisis lógico de la solución recursiva

Como en muchos acertijos matemáticos, encontrar una solución se hace más fácil al resolver un problema un poco más general: cómo mover una torre de discos de h (altura) desde una clavija inicial f< /i> = A (desde) a una clavija de destino t = C (hacia), siendo B el la tercera clavija restante y suponiendo t ≠ f. Primero, observe que el problema es simétrico para las permutaciones de los nombres de las clavijas (grupo simétrico S3). Si se conoce una solución al pasar de la clavija A a la clavija C, entonces, al cambiar el nombre de las clavijas, se puede usar la misma solución para todas las demás opciones de clavija de inicio y de destino. Si solo hay un disco (o incluso ninguno), el problema es trivial. Si h = 1, simplemente mueva el disco de la clavija A a la clavija C. Si h > 1, luego en algún lugar a lo largo de la secuencia de movimientos, el disco más grande debe moverse de la clavija A a otra clavija, preferiblemente a la clavija C. La única situación que permite este movimiento es cuando todos los discos h − 1 más pequeños están en la clavija B. Por lo tanto, primero todos los h − 1 discos más pequeños deben ir de A a B. Luego mueve el disco más grande y finalmente mueve los h − 1 discos más pequeños de la clavija B a la clavija C. La presencia del disco más grande no impide ningún movimiento de los discos más pequeños h − 1 y puede ignorarse temporalmente. Ahora el problema se reduce a mover h − 1 discos de una clavija a otra, primero de A a B y luego de B a C, pero se puede usar el mismo método en ambas ocasiones cambiando el nombre de las clavijas. Se puede usar la misma estrategia para reducir el problema h − 1 a h − 2, h − 3, y así sucesivamente hasta que solo un disco es izquierda. Esto se llama recursividad. Este algoritmo se puede esquematizar de la siguiente manera.

Identifique los discos en orden de tamaño creciente por los números naturales desde 0 hasta pero sin incluir h. Por lo tanto, el disco 0 es el más pequeño y el disco h − 1 el más grande.

El siguiente es un procedimiento para mover una torre de h discos de una clavija A a una clavija C, con B siendo la tercera clavija restante:

1. Si h ≤ 1, luego utilizar primero este procedimiento para mover el h − 1 discos más pequeños de peluca A peg B.
2. Ahora el disco más grande, es decir, disco h se puede mover de la peluca A peg C.
3. Si h ît 1, luego utilizar de nuevo este procedimiento para mover el h − 1 discos más pequeños de peluca B peg C.

Mediante la inducción matemática, se demuestra fácilmente que el procedimiento anterior requiere el número mínimo de movimientos posibles y que la solución producida es la única con este número mínimo de movimientos. Utilizando relaciones de recurrencia, el número exacto de movimientos que esta solución requiere puede calcularse mediante: ${displaystyle 2^{h}-1}$. Este resultado se obtiene notando que los pasos 1 y 3 toman ${displaystyle T_{h-1}$ movimientos, y el paso 2 toma un movimiento, dando ${displaystyle T_{h}=2T_{h-1}+1}$.

Implementación recursiva

El siguiente código de Python demuestra la solución recursiva.

A = [3, 2, 1]B = []C = []def Muévanse.()n, fuente, objetivo, auxiliar): si n ■ 0: # Mover n - 1 discos de fuente a auxiliar, por lo que están fuera del camino Muévanse.()n - 1, fuente, auxiliar, objetivo) # Mover el disco nth de la fuente al objetivo objetivo.apéndice()fuente.pop()) # Mostrar nuestro progreso impresión()A, B, C, ################################################################################################################################################################################################################################################################ ', sep='n') # Mover el n - 1 discos que dejamos en auxiliar en el objetivo Muévanse.()n - 1, auxiliar, objetivo, fuente)# Inicie la llamada de la fuente A al objetivo C con auxiliar BMuévanse.()3, A, C, B)

Solución no recursiva

La lista de movimientos de una torre que se lleva de una clavija a otra, tal como la produce el algoritmo recursivo, tiene muchas regularidades. Al contar los movimientos a partir de 1, el ordinal del disco que se moverá durante el movimiento m es el número de veces que m se puede dividir por 2. Por lo tanto, cada movimiento impar implica el disco más pequeño. También se puede observar que el disco más pequeño atraviesa las clavijas f, t, r, f, t, r, etc. para altura impar de la torre y atraviesa las clavijas f, r, t , f, r, t, etc. para una altura uniforme de la torre. Esto proporciona el siguiente algoritmo, que es más fácil de realizar a mano que el algoritmo recursivo.

En movimientos alternativos:

• Mueva el disco más pequeño a la peluca que no ha venido recientemente.
• Mueva otro disco legalmente (sólo habrá una posibilidad).

Para el primer movimiento, el disco más pequeño va a la clavija t si h es impar y a la clavija r si h es par.

Observa también que:

• Discos cuyos ordinal tienen incluso paridad moverse en el mismo sentido que el disco más pequeño.
• Discos cuyos ordinal tienen paridad extraña se mueven en sentido opuesto.
• Si h es incluso, la tercera peluca restante durante movimientos sucesivos es t, r, f, t, r, f, etc.
• Si h es extraño, la tercera peluca restante durante movimientos sucesivos es r, t, f, r, t, f, etc.

Con este conocimiento, se puede recuperar un conjunto de discos en medio de una solución óptima sin más información de estado que las posiciones de cada disco:

• Llame a los movimientos detallados sobre el movimiento "natural" de un disco.
• Examine el disco superior más pequeño que no es disco 0, y note cuál sería su único movimiento (legal): si no hay tal disco, entonces estamos en el primer o último movimiento.
• Si ese movimiento es el movimiento "natural" del disco, entonces el disco no se ha movido desde el último movimiento del disco 0, y ese movimiento debe ser tomado.
• Si ese movimiento no es el movimiento "natural" del disco, entonces mueva el disco 0.

Solución binaria

Las posiciones del disco pueden determinarse más directamente a partir de la representación binaria (base 2) del número de movimiento (el estado inicial es el movimiento n.º 0, con todos los dígitos 0 y el estado final con todos los dígitos 1), utilizando el siguiendo las reglas:

• Hay un dígito binario (bit) para cada disco.
• El bit más significativo (izquierda) representa el disco más grande. Un valor de 0 indica que el disco más grande está en el peg inicial, mientras que un 1 indica que está en el peg final (perro derecho si el número de discos es extraño y peluca media de otra manera).
• El bitstring se lee de izquierda a derecha, y cada bit se puede utilizar para determinar la ubicación del disco correspondiente.
• Un poco con el mismo valor que el anterior significa que el disco correspondiente está apilado en la parte superior del disco anterior en la misma peluca.

  (Es decir: una secuencia recta de 1s o 0s significa que los discos correspondientes están todos en el mismo peg.)

• Un poco con un valor diferente al anterior significa que el disco correspondiente es una posición a la izquierda o a la derecha del anterior. Si es izquierda o derecha se determina por esta regla:
  • Supongamos que la peluca inicial está a la izquierda.
  • También asume "rompiendo" – por lo que la peluca derecha cuenta como una "izquierda" de la peluca izquierda, y viceversa.
  • Vamos n ser el número de discos mayores que se encuentran en la misma peg que su primer disco mayor y añadir 1 si el disco más grande está en la peg izquierda. Si n es incluso, el disco se encuentra un peg a la derecha, si n es extraño, el disco situado un peg a la izquierda (en caso de incluso número de discos y viceversa de otro modo).

Por ejemplo, en un Hanoi de 8 discos:

• Muévete 0 = 00000000.
  • El disco más grande es 0, por lo que está en la peluca izquierda (inicial).
  • Todos los demás discos son 0 también, por lo que están apilados encima de él. De ahí que todos los discos estén en la peluca inicial.
• Mover 2⁸ − 1 = 11111111.
  • El disco más grande es 1, por lo que está en la peluca media (final).
  • Todos los demás discos son 1 también, por lo que están apilados encima de él. Por lo tanto todos los discos están en la peluca final y el rompecabezas está completo.
• Mover 216₁₀ = 11011000.
  • El disco más grande es 1, por lo que está en la peluca media (final).
  • El disco dos es también 1, por lo que está apilado en la parte superior de él, en la peluca media.
  • El disco tres es 0, así que está en otra peluca. Desde n es raron = 1), es una peluca a la izquierda, es decir, en la peluca izquierda.
  • El disco cuatro es 1, así que está en otra peluca. Desde n es raron = 1), es una peluca a la izquierda, es decir, en la peluca derecha.
  • Disk 5 es también 1, por lo que se apila encima de ella, en la peluca derecha.
  • El disco seis es 0, así que está en otra peluca. Desde n es incluso (n = 2), el disco es una peluca a la derecha, es decir, en la peluca izquierda.
  • Los discos siete y ocho también son 0, por lo que están apilados en la parte superior de ella, en la peluca izquierda.

Las clavijas de origen y destino para el movimiento mésimo también se pueden encontrar elegantemente a partir de la representación binaria de m utilizando operaciones bit a bit. Para usar la sintaxis del lenguaje de programación C, mover m es de peg (m & m - 1) % 3 a peg ((m | m - 1) + 1) % 3, donde los discos comienzan en la clavija 0 y terminan en la clavija 1 o 2 según el número de discos sea par o impar. Otra formulación es de peg (m - (m & -m)) % 3 a peg (m + (m & -m)) % 3.

Además, el disco que se moverá está determinado por la cantidad de veces que el conteo de movimientos (m) se puede dividir por 2 (es decir, la cantidad de bits cero a la derecha), contando la primera mover como 1 e identificando los discos por los números 0, 1, 2, etc. en orden creciente de tamaño. Esto permite una implementación informática no recursiva muy rápida para encontrar las posiciones de los discos después de m movimientos sin referencia a ningún movimiento previo o distribución de discos.

La operación, que cuenta el número de ceros consecutivos al final de un número binario, da una solución simple al problema: los discos se numeran desde cero, y al mover m, número de disco contar los ceros finales se mueve la distancia mínima posible hacia la derecha (girando hacia la izquierda según sea necesario).

Solución de código gris

El sistema numérico binario de los códigos Gray ofrece una forma alternativa de resolver el rompecabezas. En el sistema Gray, los números se expresan en una combinación binaria de 0 y 1, pero en lugar de ser un sistema numérico posicional estándar, el código Gray opera bajo la premisa de que cada valor difiere de su predecesor por solo un bit (y exactamente uno). cambió.

Si uno cuenta en código Gray de un tamaño de bit igual al número de discos en una Torre de Hanoi en particular, comienza en cero y cuenta hacia arriba, entonces el bit cambiado en cada movimiento corresponde al disco a mover, donde menos- el bit significativo es el disco más pequeño y el bit más significativo es el más grande.

Contando se mueve de 1 e identificando los discos por números a partir de 0 para aumentar el tamaño, el ordinal del disco para ser movido durante el movimiento m es el número de veces m puede dividirse por 2.

Esta técnica identifica qué disco mover, pero no hacia dónde moverlo. Para el disco más pequeño, siempre hay dos posibilidades. Para los otros discos siempre hay una posibilidad, excepto cuando todos los discos están en la misma clavija, pero en ese caso o es el disco más pequeño el que debe moverse o el objetivo ya se ha logrado. Afortunadamente, hay una regla que dice dónde mover el disco más pequeño. Sea f la clavija inicial, t la clavija de destino y r la tercera clavija restante. Si el número de discos es impar, el disco más pequeño gira a lo largo de las clavijas en el orden f → t → r → f< /i> → t → r, etc. Si el número de discos es par, se debe invertir: f → r → t → f → r → t, etc.

La posición del cambio de bit en la solución del código Gray da el tamaño del disco movido en cada paso: 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1,... (secuencia A001511 en el OEIS), una secuencia también conocida como función de regla, o una más que la potencia de 2 dentro del número de movimiento. En Wolfram Language, IntegerExponent[Range[2^8 - 1], 2] + 1 da movimientos para el rompecabezas de 8 discos.

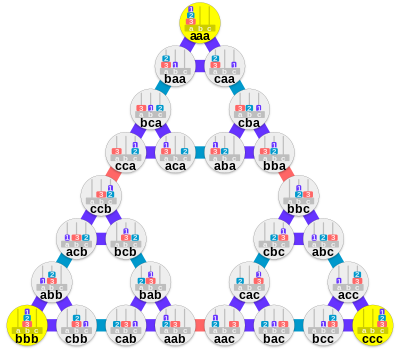
Representación gráfica

El juego se puede representar mediante un gráfico no dirigido, los nodos representan distribuciones de discos y los bordes representan movimientos. Para un disco, el gráfico es un triángulo:

La gráfica de dos discos son tres triángulos conectados para formar las esquinas de un triángulo más grande.

Se agrega una segunda letra para representar el disco más grande. Claramente, inicialmente no se puede mover.

El pequeño triángulo superior ahora representa las posibilidades de un movimiento con dos discos:

Los nodos en los vértices del triángulo exterior representan distribuciones con todos los discos en la misma clavija.

Para h + 1 discos, tome la gráfica de h discos y reemplace cada pequeño triángulo con la gráfica de dos discos.

Para tres discos el gráfico es:

El gráfico del juego del nivel 7 muestra la relación con el triángulo Sierpiński.

• llamar a las pelucas a, b, y c
• lista de posiciones de disco de izquierda a derecha en orden de tamaño creciente

Los lados del triángulo exterior representan las formas más cortas de mover una torre de una clavija a otra. El borde en el medio de los lados del triángulo más grande representa un movimiento del disco más grande. El borde en el medio de los lados de cada siguiente triángulo más pequeño representa un movimiento de cada siguiente disco más pequeño. Los lados de los triángulos más pequeños representan movimientos del disco más pequeño.

En general, para un rompecabezas con n discos, hay 3n nodos en el gráfico; cada nodo tiene tres aristas con respecto a otros nodos, excepto los tres nodos de las esquinas, que tienen dos: siempre es posible mover el disco más pequeño a una de las otras dos clavijas, y es posible mover un disco entre esas dos clavijas excepto en la situación en la que todos los discos están apilados en una clavija. Los nodos de las esquinas representan los tres casos en los que todos los discos están apilados en una clavija. El diagrama para n + 1 discos se obtiene tomando tres copias del diagrama de n-disco, cada una de las cuales representa todos los estados y movimientos de los discos más pequeños para una posición particular del nuevo disco más grande, y uniéndolos en las esquinas con tres nuevos bordes, que representan las únicas tres oportunidades para mover el disco más grande. La figura resultante tiene 3ⁿ⁺¹ nodos y todavía le quedan tres esquinas con solo dos bordes.

A medida que se agreguen más discos, la representación gráfica del juego se parecerá a una figura fractal, el triángulo de Sierpiński. Está claro que la gran mayoría de las posiciones del rompecabezas nunca se alcanzarán si se utiliza la solución más corta posible; de hecho, si los sacerdotes de la leyenda están usando la solución más larga posible (sin volver a visitar ninguna posición), les tomará 3⁶⁴ − 1 movimientos, o más de 10^{23 años.}

La forma no repetitiva más larga para tres discos se puede visualizar borrando los bordes no utilizados:

Dicho sea de paso, esta ruta no repetitiva más larga se puede obtener prohibiendo todos los movimientos de a a c.

El ciclo hamiltoniano para tres discos es:

Los gráficos muestran claramente que:

• De cada distribución arbitraria de discos, hay exactamente una forma más corta de mover todos los discos en uno de los tres pegs.
• Entre cada par de distribuciones arbitrarias de discos hay uno o dos caminos más cortos diferentes.
• De cada distribución arbitraria de discos, hay uno o dos caminos no autocrossing más largos diferentes para mover todos los discos a uno de los tres pegs.
• Entre todos los pares de distribuciones arbitrarias de discos hay uno o dos caminos no autocrossing más largos diferentes.
• Vamos N_h ser el número de caminos que no se cruzan para mover una torre de h discos de un peg a otro. Entonces:
  • N₁ = 2
  • N_{h+ 1} =N_h)² +N_h)³

Esto le da a N_h 2, 12, 1872, 6563711232,... (secuencia A125295 en la OEIS)

Variaciones

Clavijas adyacentes

Si todos los movimientos deben realizarse entre clavijas adyacentes (es decir, dadas las clavijas A, B, C, uno no puede moverse directamente entre las clavijas A y C), entonces mover una pila de n discos de la clavija A a la clavija C toma 3ⁿ − 1 movimientos. La solución utiliza las 3ⁿ posiciones válidas, tomando siempre la jugada única que no deshace la jugada anterior. La posición con todos los discos en la clavija B se alcanza a la mitad, es decir, después de (3ⁿ − 1) / 2 movimientos.

Hanoi cíclica

(feminine)

En Cyclic Hanoi, nos dan tres clavijas (A, B, C), que están dispuestas como un círculo con las direcciones en el sentido de las agujas del reloj y en el sentido contrario a las agujas del reloj definidas como A – B – C – A y A – C – B – A respectivamente. La dirección de movimiento del disco debe ser en el sentido de las agujas del reloj. Basta con representar la secuencia de discos a mover. La solución se puede encontrar utilizando dos procedimientos mutuamente recursivos:

Para mover n discos en sentido contrario a las agujas del reloj a la clavija de destino vecina:

1. Muévanse. n − 1 discos contra reloj a la peluca objetivo
2. mover el discon un paso en el reloj
3. Muévanse. n − 1 discos en el reloj a la peluca de inicio
4. mover el discon un paso en el reloj
5. Muévanse. n − 1 discos contra reloj a la peluca objetivo

Para mover n discos en el sentido de las agujas del reloj a la clavija de destino vecina:

1. Muévanse. n − 1 discos contra reloj a un peluca de repuesto
2. mover el discon un paso en el reloj
3. Muévanse. n − 1 discos contra reloj a la peluca objetivo

Supongamos que C(n) y A(n) representan el movimiento de n discos en sentido horario y antihorario, luego podemos escribir ambas fórmulas:

 C(n) = A(n-1) n A(n-1) y A(n) = A(n-1) n C(n-1) n A(n-1).

Así, C(1) = 1 y A(1) = 1 1,
C(2) = 1 1 2 1 y A(2) = 1 2 1 2 1 1.

La solución para el cíclico Hanoi tiene algunas propiedades interesantes:

1) Los patrones de movimiento de transferir una torre de discos de una clavija a otra clavija son simétricos con respecto a los puntos centrales.

2) El disco más pequeño es el primero y el último disco en moverse.

3) Los grupos de los movimientos de disco más pequeños se alternan con movimientos individuales de otros discos.

4) El número de movimientos de discos especificados por C(n) y A(n) es mínimo.

Con cuatro clavijas y más

Aunque la versión de tres clavijas tiene una solución recursiva simple conocida desde hace mucho tiempo, la solución óptima para el problema de la Torre de Hanoi con cuatro clavijas (llamado rompecabezas de Reve) no fue verificada hasta 2014 por Bousch.

Sin embargo, en el caso de cuatro o más clavijas, el algoritmo de Frame-Stewart se conoce sin prueba de optimización desde 1941.

Para la derivación formal del número exacto de movimientos mínimos necesarios para resolver el problema mediante la aplicación del algoritmo de Frame-Stewart (y otros métodos equivalentes), consulte el siguiente artículo.

Para conocer otras variantes del problema de la Torre de Hanoi de cuatro clavijas, consulte el estudio de Paul Stockmeyer.

Las configuraciones de juego denominadas Torres de Bucarest y Torres de Klagenfurt producen códigos Gray ternarios y pentarios.

Algoritmo Frame-Stewart

El algoritmo de Frame-Stewart se describe a continuación:

• Vamos ${displaystyle n}$ sea el número de discos.
• Vamos ${displaystyle r}$ sea el número de pelucas.
• Define ${displaystyle T(n,r)}$ para ser el número mínimo de movimientos requeridos para transferir discos n utilizando pelgs r.

El algoritmo se puede describir recursivamente:

1. Para algunos ${displaystyle k}$, ${displaystyle 1leq k maden}$, transferir la parte superior ${displaystyle k}$ discos a una sola peluca que no sea el inicio o destino pelucas, tomando ${displaystyle T(k,r)}$ Se mueve.
2. Sin perturbar la peluca que ahora contiene la parte superior ${displaystyle k}$ discos, transferir el resto ${displaystyle No.$ discos a la peluca de destino, utilizando sólo el resto ${displaystyle r-1}$ pelucas, tomando ${displaystyle T(n-k,r-1)}$ Se mueve.
3. Por último, transferir la parte superior ${displaystyle k}$ discos a la peluca de destino, tomando ${displaystyle T(k,r)}$ Se mueve.

Todo el proceso toma ${displaystyle 2T(k,r)+T(n-k,r-1)}$ Se mueve. Por lo tanto, la cuenta ${displaystyle k}$ debe ser elegido para el cual esta cantidad es mínima. En el caso 4-peg, el óptimo ${displaystyle k}$ iguales ${displaystyle n-leftlfloor {fnfn} {fnfnfnK}}gnfnfnfnfn}gnfncHFF} +1}$, donde ${displaystyle leftlfloor cdot rightrceil }$ es la función de entero más cercana. Por ejemplo, en el curso UPenn CIS 194 en Haskell, la primera página de asignación enumera la solución óptima para el caso 15-disk y 4-peg como 129 pasos, que se obtiene para el valor anterior k.

Se supone que este algoritmo es óptimo para cualquier número de clavijas; su número de movimientos es 2^{Θ(n1/(r−2))} (para fijos r).

Rutas generales más cortas y el número 466/885

Una curiosa generalización del objetivo original del rompecabezas es comenzar con una configuración dada de los discos donde todos los discos no están necesariamente en la misma clavija y llegar en un número mínimo de movimientos a otra configuración dada. En general, puede ser bastante difícil calcular una secuencia de movimientos más corta para resolver este problema. Andreas Hinz propuso una solución y se basa en la observación de que en una secuencia de movimientos más corta, el disco más grande que debe moverse (obviamente, uno puede ignorar todos los discos más grandes que ocuparán la misma clavija tanto en el inicial como en el final). configuraciones finales) se moverá exactamente una vez o exactamente dos veces.

Las matemáticas relacionadas con este problema generalizado se vuelven aún más interesantes cuando se considera el número promedio de movimientos en una secuencia más corta de movimientos entre dos configuraciones de disco inicial y final que se eligen al azar. Hinz y Chan Tat-Hung descubrieron de forma independiente (ver también ) que el número medio de movimientos en una torre de n discos viene dado por la siguiente fórmula exacta:

${displaystyle {frac {466}{885}cdot 2^{n}-{frac {1}{3}}-{frac {3}{5}cdot left({frac {1}{3}right)}{n}+left({fracfracfrac] {12}{59}}+{frac {18}{1003}{sqrt {17}right)left({frac {5+{sqrt {17}}}{18}right)}{n}+left({frac {frac}{sq}}}}{18}}}right)}{n}n}left({e)}e)}e)}e)}{sqsqe)}{sqe)}}e}}e)}{sqe)}e}sqe}e}e}sqsqsqe)} {sqe)} {sqsqsqsqsqsqsqsqfn}}}}}sqsqsqsqe}}}sqsqsq}}}}s {12}{59}-{frac {18}{1003}{sqrt {17}right)left({frac {5-{sqrt {17}}{18}right)}{n}}}} {n} {n}} {n}} {n}}}} {n}}} {n}}}}}}} {n}}}}}} {n}}}} {n}}}} {n}}}}}}}}} {n}}}}}}}}}}}} {n}}}}}}}}}}}}}}}}}}}}}}}}} {n} {n}}}}}}}}}}}}}}}}}} {n}}}}} {n}}}}}}}}}}}}}}} {n}}}}}}}}}}}}}}}}}}}}}}} {$

Para lo suficientemente grande n, sólo los términos primero y segundo no convergen a cero, por lo que obtenemos una expresión asintotica: ${displaystyle 466/885cdot 2^{n}-1/3+o(1)}$, como ${displaystyle nto infty }$. Así, intuitivamente, podríamos interpretar la fracción de ${displaystyle 466/885approx 52.6$ como representando la relación del trabajo uno tiene que realizar al pasar de una configuración escogida aleatoriamente a otra configuración escogida aleatoriamente, en relación con la dificultad de tener que cruzar el camino "más difícil" de longitud ${displaystyle 2^{n}-1}$ que implica mover todos los discos de un peg a otro. Romik dio una explicación alternativa para la aparición de la constante 466/885, así como un algoritmo nuevo y algo mejorado para calcular el camino más corto.

Hanói magnético

En la Torre Magnética de Hanoi, cada disco tiene dos lados distintos, el norte y el sur (normalmente de color 'rojo' y 'azul'). Los discos no deben colocarse con los polos similares juntos; los imanes en cada disco evitan este movimiento ilegal. Además, cada disco debe voltearse a medida que se mueve.

Configuración inicial de las Torres bicolores de Hanoi (n=4)

Torres bicolores de Hanoi

Esta variación del famoso rompecabezas de la Torre de Hanoi se ofreció a estudiantes de los grados 3 a 6 en el 2ème Championnat de France des Jeux Mathématiques et Logiques celebrado en julio de 1988.

Configuración final de las Torres bicolor de Hanoi (n=4)

Las reglas del rompecabezas son esencialmente las mismas: los discos se transfieren entre clavijas de uno en uno. En ningún momento se podrá colocar un disco más grande encima de uno más pequeño. La diferencia es que ahora para cada tamaño hay dos discos: uno negro y otro blanco. Además, ahora hay dos torres de discos de colores alternos. El objetivo del rompecabezas es hacer que las torres sean monocromáticas (del mismo color). Se supone que los discos más grandes en la parte inferior de las torres intercambian posiciones.

Torre de Hanói

Se ha adaptado una variación del rompecabezas como un juego de solitario con nueve cartas bajo el nombre Tower of Hanoy. No se sabe si la ortografía alterada del nombre original es deliberada o accidental.

Aplicaciones

Imagen topográfica 3D AFM de nanohecha de paleladio multicapa sobre la ola de silicio, con Torre de estructura similar a Hanoi.

La Torre de Hanoi se utiliza con frecuencia en la investigación psicológica sobre resolución de problemas. También existe una variante de esta tarea denominada Torre de Londres para el diagnóstico y tratamiento neuropsicológico de las funciones ejecutivas.

Zhang y Norman utilizaron varias representaciones isomórficas (equivalentes) del juego para estudiar el impacto del efecto de representación en el diseño de tareas. Demostraron un impacto en el rendimiento del usuario al cambiar la forma en que se representan las reglas del juego, usando variaciones en el diseño físico de los componentes del juego. Este conocimiento ha impactado en el desarrollo del marco TURF para la representación de la interacción humano-computadora.

La Torre de Hanoi también se utiliza como esquema de rotación de copias de seguridad cuando se realizan copias de seguridad de datos informáticos en las que intervienen varias cintas/medios.

Como se mencionó anteriormente, la Torre de Hanoi es popular para enseñar algoritmos recursivos a estudiantes principiantes de programación. Una versión pictórica de este rompecabezas está programada en el editor de emacs, al que se accede escribiendo M-x hanoi. También hay un algoritmo de muestra escrito en Prolog.

La Torre de Hanoi también es utilizada como prueba por neuropsicólogos que intentan evaluar los déficits del lóbulo frontal.

En 2010, los investigadores publicaron los resultados de un experimento que encontró que la especie de hormiga Linepithema humile pudo resolver con éxito la versión de 3 discos del problema de la Torre de Hanoi a través de dinámicas no lineales y señales de feromonas

En 2014, los científicos sintetizaron nanoláminas de paladio de varias capas con una estructura similar a la de la Torre de Hanoi.

En la cultura popular

En la historia de ciencia ficción "Now Inhale", de Eric Frank Russell, un humano es prisionero en un planeta donde la costumbre local es hacer que el prisionero juegue un juego hasta que lo gane o lo pierda antes. su ejecución. El protagonista sabe que un barco de rescate puede tardar un año o más en llegar, por lo que elige jugar Towers of Hanoi con 64 discos. Esta historia hace referencia a la leyenda de los monjes budistas jugando el juego hasta el fin del mundo.

En la historia de Doctor Who de 1966 The Celestial Toymaker, el villano del mismo nombre obliga al Doctor a jugar un juego de diez piezas de 1023 movimientos de la Torre de Hanoi titulado The Trilogic Game. con las piezas formando una pirámide cuando se apilan.

En 2007, el concepto del problema de las Torres de Hanoi se usó en El profesor Layton y la caja diabólica en los rompecabezas 6, 83 y 84, pero los discos se cambiaron por panqueques. El rompecabezas se basó en un dilema en el que el chef de un restaurante tenía que mover una pila de panqueques de un plato a otro con los principios básicos del rompecabezas original (es decir, tres platos a los que se podían mover los panqueques, sin poder moverlos). poner un panqueque más grande sobre uno más pequeño, etc.)

En la película Rise of the Planet of the Apes (2011), este rompecabezas, llamado en la película "Lucas Tower", se utiliza como prueba para estudiar la inteligencia de los simios.

El rompecabezas aparece regularmente en juegos de aventura y rompecabezas. Dado que es fácil de implementar y reconocer, es ideal para usarlo como un rompecabezas en un juego gráfico más grande (por ejemplo, Star Wars: Knights of the Old Republic y Mass Effect< /i>). Algunas implementaciones usan discos rectos, pero otras disfrazan el rompecabezas de alguna otra forma. Hay una versión arcade de Sega.

Una versión de 15 discos del rompecabezas aparece en el juego Sunless Sea como la cerradura de una tumba. El jugador tiene la opción de hacer clic en cada movimiento del rompecabezas para resolverlo, pero el juego señala que se necesitarán 32767 movimientos para completarlo. Si un jugador especialmente dedicado hace clic hasta el final del rompecabezas, se revela que completar el rompecabezas no abre la puerta.

En Yu-Gi-Oh! VRAINS, un grupo de hackers llamado "Knight of Hanoi" crear una estructura llamada "Torre de Hanoi" dentro de la red homónima de realidad virtual VRAINS.

Esto se usó por primera vez como un desafío en Survivor Tailandia en 2002, pero en lugar de anillos, las piezas se hicieron para parecerse a un templo. Sook Jai lanzó el desafío de deshacerse de Jed a pesar de que Shii-Ann sabía muy bien cómo completar el rompecabezas. El problema aparece como parte de un desafío de recompensa en un episodio de 2011 de la versión estadounidense de la serie de televisión Survivor. Ambos jugadores (Ozzy Lusth y Benjamin 'Coach' Wade) lucharon por comprender cómo resolver el rompecabezas y cuentan con la ayuda de sus compañeros de tribu.