Torneo de todos contra todos

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Tipo de torneo deportivo

A torneo redondo-robin o todo el torneo es un formato de competición en el que cada concursante se reúne con cada otro participante, generalmente a su vez. Un redondeo contrasta con un torneo de eliminación, en el que los participantes se eliminan después de un cierto número de victorias o pérdidas.

Terminología

El término round-robin se deriva del término francés ruban ('cinta'). Con el tiempo, el término se transformó en robin.

En un sistema de todos contra todos, cada participante juega una vez con todos los demás participantes. Si cada participante juega con todos los demás dos veces, esto se denomina con frecuencia todos contra todos. El término rara vez se utiliza cuando todos los participantes juegan entre sí más de dos veces, y nunca se utiliza cuando un participante juega con otros un número desigual de veces, como es el caso en casi todas las principales ligas deportivas profesionales de América del Norte.

En el Reino Unido, un torneo de todos contra todos se ha denominado torneo americano en deportes como el tenis o el billar, que suelen tener torneos de eliminación simple (o "knockout"), aunque ahora esto rara vez se hace.

Un torneo de todos contra todos con cuatro jugadores a veces se denomina "quad" o "foursome".

Aplicaciones

En los deportes con un gran número de partidos competitivos por temporada, los torneos de todos contra todos son comunes. La mayoría de las ligas de fútbol del mundo se organizan con un sistema de todos contra todos, en el que cada equipo juega contra todos los demás de su liga una vez en casa y otra fuera. Este sistema también se utiliza en la clasificación para los torneos más importantes, como la Copa Mundial de la FIFA y los torneos continentales (por ejemplo, el Campeonato Europeo de la UEFA, la Copa de Oro de la CONCACAF, la Copa Asiática de la AFC, la Copa América de la CONMEBOL y la Copa de Naciones de la CAF). También hay torneos de todos contra todos de bridge, ajedrez, damas, go, hockey sobre hielo, curling y Scrabble. El Campeonato Mundial de Ajedrez decidió en 2005 y en 2007 un torneo de todos contra todos con ocho jugadores, en el que cada jugador se enfrenta a todos los demás jugadores una vez con las blancas y otra con las negras.

En un ejemplo más extremo, la Liga KBO de béisbol juega con un sistema de todos contra todos de 16 partidos, en el que cada uno de los 10 equipos juega 16 veces entre sí, para un total de 144 partidos por equipo.

LIDOM (Baseball Winter League in the Dominican Republic) juega un 18-fold round robin como un torneo semi final entre cuatro equipos clasificados.

Las clasificaciones de los torneos de grupos suelen basarse en el número de partidos ganados y empatados, y en una variedad de criterios de desempate.

Con frecuencia, las fases de grupos de un torneo más amplio se disputan con un sistema de todos contra todos. Entre los ejemplos de este sistema se incluyen la Copa Mundial de la FIFA, la Eurocopa de fútbol de la UEFA y la Copa de la UEFA (2004-2009) en fútbol, el Super Rugby (rugby union) en el hemisferio sur durante sus iteraciones pasadas como Super 12 y Super 14 (pero no en sus formatos posteriores de 15 y 18 equipos), la Copa Mundial de Críquet junto con la Liga Premier de la India, el importante torneo Twenty-20 Cricket y muchas conferencias universitarias de fútbol americano, como la Conference USA (que actualmente tiene 9 miembros). Las fases de grupos de las competiciones de clubes de la UEFA y la Copa Libertadores se disputan con un sistema de todos contra todos, al igual que la mayoría de las ligas de baloncesto fuera de los Estados Unidos, incluida la temporada regular de la Euroliga (así como su antigua fase Top 16); la United Football League ha utilizado un sistema de todos contra todos doble para sus temporadas de 2009 y 2010.

Los torneos de tenis de fin de temporada también utilizan un formato de todos contra todos antes de las etapas de semifinales.

Evaluación

Ventajas

El campeón de un torneo de todos contra todos es el concursante que gana más partidas, excepto cuando hay posibilidad de empate.

En teoría, un torneo de todos contra todos es la forma más justa de determinar al campeón entre un número conocido y fijo de participantes. Cada participante, ya sea jugador o equipo, tiene las mismas posibilidades contra todos los demás oponentes porque no hay una clasificación previa de los participantes que impida un partido entre una pareja determinada. Se considera que el elemento de suerte es menor en comparación con un sistema de eliminación directa, ya que una o dos malas actuaciones no tienen por qué arruinar las posibilidades de un competidor de obtener la victoria final. Los registros finales de los participantes son más precisos, en el sentido de que representan los resultados durante un período más largo contra el mismo oponente.

El sistema también es mejor para clasificar a todos los participantes, no solo para determinar al ganador. Esto es útil para determinar la clasificación final de todos los competidores, del más fuerte al más débil, para fines de clasificación para otra etapa o competencia, así como para premios en efectivo.

En los deportes de equipo, los campeones de las grandes ligas en formato de todos contra todos son considerados generalmente como el "mejor" equipo del país, en lugar de los ganadores de la copa, cuyos torneos suelen seguir un formato de eliminación simple.

Además, en torneos como las Copas Mundiales de la FIFA o la ICC, una primera ronda que consiste en una serie de mini round robins entre grupos de 4 equipos evita la posibilidad de que un equipo viaje posiblemente miles de kilómetros sólo para ser eliminado después de una sola mala actuación en un sistema de eliminación directa. Los primeros uno, dos o, en ocasiones, tres equipos de estos grupos pasan entonces a una etapa de eliminación directa para el resto del torneo.

En el círculo de la muerte (ver más abajo), es posible que no surja ningún campeón de un torneo de todos contra todos, incluso si no hay sorteo. Sin embargo, la mayoría de los deportes tienen sistemas de desempate que resuelven este problema.

Desventajas

Los robines redondos pueden sufrir demasiado tiempo en comparación con otros tipos de torneo, y con los juegos programados más tarde potencialmente no tienen ningún significado sustancial. También pueden requerir procedimientos de combate.

Los torneos del sistema suizo intentan combinar elementos de los formatos de round-robin y eliminación, para proporcionar un campeón digno usando menos rondas que un round robin, mientras que permite sorteos y pérdidas.

Longitud del torneo

La principal desventaja de un torneo de round robin es el tiempo necesario para completarlo. A diferencia de un torneo de nocaut en el que la mitad de los participantes son eliminados después de cada ronda, una round robin requiere una ronda menos que el número de participantes. Por ejemplo, un torneo de 16 equipos se puede completar en solo 4 rondas (es decir, 15 partidos) en un formato de eliminación; Un formato de torneo de doble eliminación requiere 30 (o 31) partidos, pero una redonda requeriría 15 rondas (es decir, 120 partidos) para terminar si cada competidor se enfrenta una vez.

Otros problemas provienen de la diferencia entre la equidad teórica del formato y la práctica de Round Robin en un evento real. Dado que el vencedor se ha llegado gradualmente a través de múltiples rondas de juego, los equipos que se desempeñan mal, que podrían haber sido eliminados rápidamente de la contención del título, se ven obligados a jugar sus juegos restantes. Por lo tanto, los juegos se juegan tarde en la competencia entre competidores sin posibilidades de éxito restantes. Además, algunos partidos posteriores emparejarán un competidor que le quede algo para jugar contra otro que no. También puede ser posible que un competidor juegue a los oponentes más fuertes en un round robin en rápida sucesión, mientras que otros los juegan de manera intermitente con una oposición más débil. Esta asimetría significa que jugar a los mismos oponentes no es necesariamente completamente equitativo.

Tampoco hay un partido final programado a menos que (por coincidencia) dos competidores se encuentren en el último partido del torneo, con el resultado de ese partido que determina el campeonato. Una instancia notable de este evento fue el partido de la Copa Mundial de la FIFA de 1950 entre Uruguay y Brasil.

equipos calificados

surgen más problemas cuando se usa un round-robin como una ronda de clasificación dentro de un torneo más grande. Un competidor ya se clasificó para la siguiente etapa antes de su último juego puede no esforzarse (para conservar los recursos para la próxima fase) o incluso perder deliberadamente (si el oponente de la siguiente fase programado para un clasificatorio de menor posición se percibe más fácil que para uno más alto).

Cuatro pares en los dobles de los Juegos Olímpicos de 2012 de Badminton, habiéndose calificado para la próxima ronda, fueron expulsados de la competencia por intentar perder en la etapa de Round Robin para evitar compatriotas y oponentes mejor clasificados. La etapa Round Robin en los Juegos Olímpicos fue una nueva introducción, y estos problemas potenciales se conocieron fácilmente antes del torneo; Se realizaron cambios antes de los próximos Juegos Olímpicos para evitar una repetición de estos eventos.

Círculo de muerte

Otra desventaja, especialmente en robines redondos más pequeños, es el " Circle of Death ", donde los equipos no pueden separarse en un récord de la cabeza a cabeza. En un robo redondo de tres equipos, donde A derrota B, B derrota a C y C derrota a A, los tres competidores tendrán un récord de una victoria y una derrota, y un desempate deberá usarse para separar a los equipos. Esto ocurrió durante el Grupo E de la Copa Mundial de la FIFA de 1994, donde los cuatro equipos terminaron con un récord de una victoria, un empate y una derrota. Este fenómeno es análogo a la paradoja de Condorcet en la teoría de votación.

Algoritmo de programación

Si ${displaystyle n}$ es el número de competidores, un torneo de round robin puro requiere ${displaystyle {begin{matrix}{frac {n}{2}}end{matrix}}(n-1)}$ juegos. Si ${displaystyle n}$ es incluso, entonces en cada uno de ${displaystyle (n-1)}$ rondas, ${displaystyle {begin{matrix}{frac {n}{2}}end{matrix}}}$ juegos se pueden ejecutar simultáneamente, siempre y cuando existan recursos suficientes (por ejemplo, pistas para un torneo de tenis). Si ${displaystyle n}$ es extraño, habrá ${displaystyle n}$ rondas, cada una con ${displaystyle {begin{matrix}{frac {n-1}{2}}end{matrix}}}$ juegos, y un competidor sin juego en esa ronda.

Método de círculo

El método del círculo es un algoritmo simple para crear un cronograma para un torneo de todos contra todos. A todos los competidores se les asignan números y luego se los empareja en la primera ronda:

Ronda 1. (1 obras 14, 2 obras 13,...)
1	2	3	4	5	6	7
14	13	12	11	10	9	8

A continuación, se fija uno de los competidores en la primera o última columna de la tabla (el número uno en este ejemplo) y los demás se rotan una posición en el sentido de las agujas del reloj.

Ronda 2. (1 obras 13, 14 obras 12,...)
1	14	2	3	4	5	6
13	12	11	10	9	8	7

Ronda 3. (1 obras 12, 13 obras 11,...)
1	13	14	2	3	4	5
12	11	10	9	8	7	6

Esto se repite hasta que se llega casi a la posición inicial:

Ronda 13. (1 obras 2, 3 obras 14,...)
1	3	4	5	6	7	8
2	14	13	12	11	10	9

Para ver eso - con un número uniforme ${displaystyle n}$ de competidores - este algoritmo se da cuenta de cada posible combinación de ellos (equivalentemente, que todos los pares realizados son pares diferentes), argumentamos como sigue.

Primero, el algoritmo obviamente se da cuenta de cada par de competidores si uno de ellos iguala ${displaystyle 1}$ (el competidor que no se mueve).

Siguiente, para pares de no- ${displaystyle 1}$ competidores, que su distancia sea el número $<math alttext="{displaystyle kkc)n2{displaystyle k made{frac {n}{2}}<img alt="{displaystyle k$ de veces la rotación tiene que realizarse para que un competidor llegue a la posición que el otro tenía.

En el ejemplo dado ( ${displaystyle n=14}$ ), ${displaystyle 2}$ tiene distancia ${displaystyle 1}$ a ${displaystyle 3}$ y a ${displaystyle 14}$ y tiene distancia ${displaystyle 6}$ a ${displaystyle 8}$ y a ${displaystyle 9}$ .

En una ronda, una posición no óptima (no incluyendo ${displaystyle 1}$ ) sólo puede ser tomado por los competidores de una distancia fija. En redondo ${displaystyle 1}$ del ejemplo, en la segunda posición competidor ${displaystyle 2}$ contra ${displaystyle 13}$ , su distancia ${displaystyle 2}$ . En redondo ${displaystyle 2}$ , esta posición es sostenida por los competidores ${displaystyle 14}$ y ${displaystyle 12}$ , también teniendo distancia ${displaystyle 2}$ , etc. Del mismo modo, la siguiente posición ( ${displaystyle 3}$ contra la ${displaystyle 12}$ en redondo ${displaystyle 1}$ , ${displaystyle 2}$ contra la ${displaystyle 11}$ en redondo ${displaystyle 2}$ , etc.) sólo puede mantener la distancia- ${displaystyle 4}$ competidores.

Por todos $<math alttext="{displaystyle kkc)n2{displaystyle k made{frac {n}{2}}<img alt="{displaystyle k$ , hay exactamente ${displaystyle n-1}$ pares de distancia ${displaystyle k}$ . Hay ${displaystyle n-1}$ rondas y todos se dan cuenta de una distancia- ${displaystyle k}$ par en la misma posición. Claramente, estos pares son dos veces diferentes. La conclusión es que cada distancia... ${displaystyle k}$ par se realiza.

Esto es para todos. ${displaystyle k}$ Por lo tanto, cada par se realiza.

Si hay un número impar de competidores, se puede agregar un competidor ficticio, cuyo oponente programado en una ronda determinada no juega y tiene un bye. Por lo tanto, el cronograma se puede calcular como si el competidor ficticio fuera un jugador común, ya sea fijo o rotativo.

En lugar de girar una posición, cualquier número relativamente primo a ${displaystyle (n-1)}$ generará un calendario completo. Las filas superiores e inferiores pueden indicar hogar/fuera en deportes, blanco/negro en ajedrez, etc.; para asegurar la equidad, esto debe alternar entre rondas ya que el competidor 1 está siempre en la primera fila. Si, por ejemplo, los competidores 3 y 8 no pudieron cumplir su fijación en la tercera ronda, tendría que ser reprogramado fuera de las otras rondas, ya que ambos competidores ya estarían enfrentando a otros oponentes en esas rondas. Las restricciones de programación más complejas pueden requerir algoritmos más complejos. Este horario se aplica en torneos de ajedrez y draughts de juegos rápidos, donde los jugadores se mueven físicamente alrededor de una mesa. En Francia se llama el sistema Carousel-Berger (Système Rutch-Berger).

El calendario también se puede utilizar para torneos de todos contra todos "asincrónicos" en los que todos los partidos tienen lugar en momentos diferentes (por ejemplo, porque sólo hay una sede). Los partidos se juegan de izquierda a derecha en cada ronda, y desde la primera ronda hasta la última. Cuando el número de competidores es par, este calendario funciona bien con respecto a las medidas de calidad y equidad, como la cantidad de descanso entre partidos. Por otro lado, cuando el número de competidores es impar, no funciona tan bien y un calendario diferente es superior con respecto a estas medidas.

Mesas Berger

Las tablas de Berger, que deben su nombre al maestro ajedrecista austríaco Johann Berger, también se utilizan ampliamente en la planificación de torneos. Berger publicó las tablas de emparejamiento en sus dos Schach-Jahrbücher (Anales de ajedrez), con la debida referencia a su inventor, Richard Schurig.

Ronda 1	1 – 14	2 – 13	3 – 12	4 – 11	5 – 10	6 – 9	7 – 8
Ronda 2	14 – 8	9 – 7	10 – 6	11 – 5	12 – 4	13 – 3	1 – 2
Ronda 3	2 a 14	3 – 1	4 – 13	5 – 12	6 – 11	7 – 10	8 – 9
...	...
Ronda 13	7 – 14	8 – 6	9 – 5	10 – 4	11 – 3	12 – 2	13 – 1

Esto constituye un cronograma en el que el jugador 14 tiene una posición fija, y todos los demás jugadores se giran en sentido contrario. ${displaystyle {frac {n}{2}}}$ posiciones. Este horario se genera manualmente. Para construir la siguiente ronda, el último jugador, número 8 en la primera vuelta, se mueve a la cabeza de la mesa, seguido por el jugador 9 contra el jugador 7, jugador 10 contra 6, hasta el jugador 1 contra el jugador 2. Aritmetically, this equates to adding ${displaystyle {frac {n}{2}}}$ a la fila anterior, con la excepción de jugador ${displaystyle n}$ . Cuando el resultado de la adición es mayor que ${displaystyle (n-1)}$ , luego restar ${displaystyle (n-1)}$ de la suma.

Este horario también puede ser representado como una tabla (n-1, n-1), expresando una ronda en la que los jugadores se reúnen entre sí. Por ejemplo, el jugador 7 juega contra el jugador 11 en la ronda 4. Si un jugador se encuentra, entonces esto muestra un adiós o un juego contra el jugador n. Todos los juegos en una ronda constituyen una diagonal en la mesa.

Diagonal Scheme
×	2	3	4	5	6	7	8	9	10	11	12	13	1	2	3	4	5	6	7	8	9	10	11	12	13
1													1	2	3	4	5	6	7	8	9	10	11	12	13
2												1	2	3	4	5	6	7	8	9	10	11	12	13
3											1	2	3	4	5	6	7	8	9	10	11	12	13
4										1	2	3	4	5	6	7	8	9	10	11	12	13
5									1	2	3	4	5	6	7	8	9	10	11	12	13
6								1	2	3	4	5	6	7	8	9	10	11	12	13
7							1	2	3	4	5	6	7	8	9	10	11	12	13
8						1	2	3	4	5	6	7	8	9	10	11	12	13
9					1	2	3	4	5	6	7	8	9	10	11	12	13
10				1	2	3	4	5	6	7	8	9	10	11	12	13
11			1	2	3	4	5	6	7	8	9	10	11	12	13
12		1	2	3	4	5	6	7	8	9	10	11	12	13
13	1	2	3	4	5	6	7	8	9	10	11	12	13

Programa de la Ronda Robin
×	1	2	3	4	5	6	7	8	9	10	11	12	13
1	1	2	3	4	5	6	7	8	9	10	11	12	13
2	2	3	4	5	6	7	8	9	10	11	12	13	1
3	3	4	5	6	7	8	9	10	11	12	13	1	2
4	4	5	6	7	8	9	10	11	12	13	1	2	3
5	5	6	7	8	9	10	11	12	13	1	2	3	4
6	6	7	8	9	10	11	12	13	1	2	3	4	5
7	7	8	9	10	11	12	13	1	2	3	4	5	6
8	8	9	10	11	12	13	1	2	3	4	5	6	7
9	9	10	11	12	13	1	2	3	4	5	6	7	8
10	10	11	12	13	1	2	3	4	5	6	7	8	9
11	11	12	13	1	2	3	4	5	6	7	8	9	10
12	12	13	1	2	3	4	5	6	7	8	9	10	11
13	13	1	2	3	4	5	6	7	8	9	10	11	12

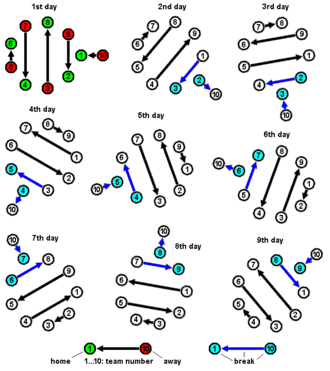
El horario anterior también puede representarse mediante un gráfico, como se muestra a continuación:

Programa de la Ronda Robin Diagrama de Span

Tanto el gráfico como el horario fueron reportados por Edouard Lucas como un rompecabezas de matemáticas recreativas. Lucas, quien describe el método como simple e ingenioso , atribuye la solución a Felix Walecki, maestra de Lycée Condorcet. Lucas también incluyó una solución alternativa por medio de un rompecabezas deslizante.

Construcción original de mesas de emparejamiento por Richard Schurig (1886)

Para un número aún ${displaystyle n}$ o un número extraño ${displaystyle n-1}$ de los competidores, Schurig construye una mesa con ${displaystyle n/2}$ filas verticales y ${displaystyle n-1}$ filas horizontales. Luego lo pobla a partir de la esquina superior izquierda repitiendo la secuencia de números de 1 hasta 1 ${displaystyle n-1}$ . Aquí hay una tabla de ejemplo para 7 o 8 competidores:

Ronda 1	1	2	3	4
Ronda 2	5	6	7	1
Ronda 3	2	3	4	5
Ronda 4	6	7	1	2
Ronda 5	3	4	5	6
Ronda 6	7	1	2	3
Ronda 7	4	5	6	7

Luego para conseguir a los oponentes se construye una segunda mesa. Cada fila horizontal ${displaystyle x}$ está poblada con los mismos números que la fila ${displaystyle x+1}$ en la tabla anterior (la última fila está poblada con números de la primera fila en la tabla original), pero en el orden inverso (de derecha a izquierda).

Ronda 1	– 1	– 7	- 6	– 5
Ronda 2	– 5	– 4	– 3	- 2
Ronda 3	- 2	– 1	– 7	- 6
Ronda 4	- 6	– 5	– 4	– 3
Ronda 5	– 3	- 2	– 1	– 7
Ronda 6	– 7	- 6	– 5	– 4
Ronda 7	– 4	– 3	- 2	– 1

Al fusionar las tablas anteriores:

Ronda 1	1 – 1	2 – 7	3 – 6	4 – 5
Ronda 2	5 – 5	6 – 4	7 – 3	1 – 2
Ronda 3	2 – 2	3 – 1	4 – 7	5 – 6
Ronda 4	6 – 6	7 – 5	1 – 4	2 – 3
Ronda 5	3 – 3	4 – 2	5 – 1	6 – 7
Ronda 6	7 – 7	1 – 6	2 – 5	3 – 4
Ronda 7	4 – 4	5 – 3	6 – 2	7 – 1

Luego se actualiza la primera columna: si el número de competidores es incluso, número de jugador ${displaystyle n}$ se sustituye alternadamente por las primeras y segundas posiciones, mientras que si el número de competidores es extraño un adiós se utiliza en su lugar.

Las tablas de emparejamiento se publicaron como anexo a las disposiciones para la celebración de torneos magistrales. Schurig no proporcionó ninguna prueba ni motivación para su algoritmo. Para más detalles históricos, véase Ahrens.

Contenido relacionado

Más resultados...