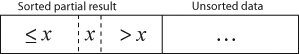Tipo de inserción

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Algoritmo de clasificación

Ordenación por inserción es un algoritmo de ordenación simple que crea la matriz ordenada final (o lista) un elemento a la vez mediante comparaciones. Es mucho menos eficiente en listas grandes que los algoritmos más avanzados, como la ordenación rápida, la ordenación en montón o la ordenación por fusión. Sin embargo, la ordenación por inserción ofrece varias ventajas:

Aplicación sencilla: Jon Bentley muestra una versión C/C++ de tres líneas que es cinco líneas cuando se optimiza.
Eficiente para (quite) pequeños conjuntos de datos, al igual que otros cuadráticos (es decir, O(n²)) clasificación de algoritmos
Más eficiente en la práctica que la mayoría de otros algoritmos cuadráticos simples como selección o tipo de burbujas
Adaptive, es decir, eficiente para conjuntos de datos que ya están substancialmente ordenados: la complejidad del tiempo es O(kn) cuando cada elemento en la entrada no es más que $k$ lugares lejos de su posición ordenada
Estable; es decir, no cambia el orden relativo de elementos con teclas iguales
En el lugar; es decir, sólo requiere una cantidad constante O(1) del espacio de memoria adicional
En línea; es decir, puede ordenar una lista como la recibe

Cuando las personas clasifican manualmente las cartas en una mano de bridge, la mayoría usa un método similar a la clasificación por inserción.

Algoritmo

Un ejemplo gráfico de tipo de inserción. La lista parcial ordenada (negro) inicialmente contiene sólo el primer elemento en la lista. Con cada iteración se elimina un elemento (rojo) de los datos de entrada "no revisados para el pedido" e insertados en el lugar en la lista clasificada.

La ordenación por inserción itera, consume un elemento de entrada en cada repetición y genera una lista de salida ordenada. En cada iteración, la ordenación por inserción elimina un elemento de los datos de entrada, encuentra la ubicación a la que pertenece dentro de la lista ordenada y lo inserta allí. Se repite hasta que no quedan elementos de entrada.

La clasificación generalmente se realiza en el lugar, iterando la matriz, aumentando la lista ordenada detrás de ella. En cada posición de matriz, verifica el valor allí con el valor más grande en la lista ordenada (que está al lado, en la posición de matriz anterior verificada). Si es más grande, deja el elemento en su lugar y pasa al siguiente. Si es más pequeño, encuentra la posición correcta dentro de la lista ordenada, desplaza todos los valores más grandes hacia arriba para hacer un espacio y los inserta en esa posición correcta.

La matriz resultante después de k iteraciones tiene la propiedad donde se ordenan las primeras k + 1 entradas ("+1" porque la primera entrada es salteado). En cada iteración, se elimina la primera entrada restante de la entrada y se inserta en el resultado en la posición correcta, extendiendo así el resultado:

se convierte

con cada elemento mayor que x copiado a la derecha mientras se compara con x.

La variante más común de ordenación por inserción, que opera en matrices, se puede describir de la siguiente manera:

Supongamos que existe una función llamada Insertar diseñado para insertar un valor en una secuencia ordenada al principio de un array. Funciona comenzando al final de la secuencia y desplazando cada elemento un lugar a la derecha hasta que se encuentre una posición adecuada para el nuevo elemento. La función tiene el efecto secundario de sobreescribir el valor almacenado inmediatamente después de la secuencia ordenada en el array.
Para realizar un tipo de inserción, comience en el elemento más izquierdo del array e invoque Insertar insertar cada elemento encontrado en su posición correcta. La secuencia ordenada en la que se inserta el elemento se almacena al principio de la matriz en el conjunto de índices ya examinados. Cada inserción sobrescribe un valor único: el valor que se inserta.

A continuación se muestra el pseudocódigo del algoritmo completo, donde las matrices están basadas en cero:

i ← 1
mientras i) longitud(A)
j ← i
 mientras j latitud 0 y A[j-1] A[j]
 Swap A[j] y A[j-1]
j ← j - 1
 terminar mientrasi ← i + 1
terminar mientras

El ciclo externo se ejecuta sobre todos los elementos excepto el primero, porque el prefijo de un solo elemento A[0:1] está ordenado de forma trivial, por lo que el invariante que el primer i están ordenadas es cierto desde el principio. El ciclo interno mueve el elemento A[i] a su lugar correcto para que, después del ciclo, se clasifiquen los primeros elementos i+1. Tenga en cuenta que el operador y en la prueba debe usar una evaluación de cortocircuito; de lo contrario, la prueba podría generar un error de límites de matriz, cuando j=0 e intenta evaluar A[j-1] > A[j] (es decir, falla el acceso a A[-1]).

Después de expandir la operación swap en el lugar como x ← A[j]; A[j] ← A[j-1]; A[j-1] ← x (donde x es una variable temporal), se puede producir una versión un poco más rápida que mueva A[i] a su posición de una sola vez y solo realiza una asignación en el cuerpo del bucle interno:

i ← 1
mientras i) longitud(A)
x ← A[i]
j ← i - 1
 mientras j 0 y A[j] rito x
A[j+1] ← A[j]
j ← j - 1
 terminar mientrasA[j+1] ← x
i ← i + 1
terminar mientras

El nuevo bucle interno desplaza los elementos hacia la derecha para despejar un lugar para x = A[i].

El algoritmo también se puede implementar de forma recursiva. La recursividad simplemente reemplaza el ciclo externo, llamándose a sí mismo y almacenando valores sucesivamente más pequeños de n en la pila hasta que n es igual a 0, donde la función regresa a la cadena de llamadas para ejecutarse el código después de cada llamada recursiva comienza con n igual a 1, con n aumentando en 1 a medida que cada instancia de la función regresa a la instancia anterior. La llamada inicial sería insertionSortR(A, length(A)-1).

función inserción SortR (array A, int n)
 si n σ 0
insertionSortR(A, n-1)
x ← A[n]
j ← n-1
 mientras j 0 y A[j] rito x
A[j+1] ← A[j]
j ← j-1
 terminar mientrasA[j+1] ← x
 terminar sifunción final

No acorta el código, tampoco reduce el tiempo de ejecución, pero aumenta el consumo de memoria adicional de $O(1)$ a $O(N)$ (en el nivel más profundo de recursividad, la pila contiene $N$ referencias a Una matriz, cada una con el valor correspondiente de la variable n desde $N$ hasta 1).

`Casos mejores, peores y promedio`

La entrada del mejor de los casos es una matriz que ya está ordenada. En este caso, la ordenación por inserción tiene un tiempo de ejecución lineal (es decir, O(n)). Durante cada iteración, el primer elemento restante de la entrada solo se compara con el elemento más a la derecha de la subsección ordenada de la matriz.

La entrada más simple para el peor de los casos es una matriz ordenada en orden inverso. El conjunto de todas las entradas del peor de los casos consta de todas las matrices donde cada elemento es el más pequeño o el segundo más pequeño de los elementos anteriores. En estos casos, cada iteración del ciclo interno escaneará y cambiará toda la subsección ordenada de la matriz antes de insertar el siguiente elemento. Esto le da a la ordenación por inserción un tiempo de ejecución cuadrático (es decir, O(n²)).

El caso promedio también es cuadrático, lo que hace que la ordenación por inserción no sea práctica para ordenar arreglos grandes. Sin embargo, la ordenación por inserción es uno de los algoritmos más rápidos para ordenar arreglos muy pequeños, incluso más rápido que la ordenación rápida; de hecho, las buenas implementaciones de ordenación rápida utilizan la ordenación por inserción para arreglos más pequeños que cierto umbral, también cuando surgen como subproblemas; el umbral exacto debe determinarse experimentalmente y depende de la máquina, pero normalmente ronda los diez.

Ejemplo: la siguiente tabla muestra los pasos para ordenar la secuencia {3, 7, 4, 9, 5, 2, 6, 1}. En cada paso, se subraya la clave en consideración. La clave que se movió (o se dejó en su lugar porque era la más grande considerada) en el paso anterior está marcada con un asterisco.

3 7 4 9 5 2 6 1
3* 7 4 9 5 2 6 1
3 7* 4 9 5 2 6 1
3 4* 7 9 5 2 6 1
3 4 7 9* 5 2 6 1
3 4 5* 7 9 2 6 1
2* 3 4 5 7 9 6 1
2 3 4 5 6* 7 9 11* 2 3 4 5 6 7 9

`Relación con otros algoritmos de clasificación`

La ordenación por inserción es muy similar a la ordenación por selección. Al igual que en la ordenación por selección, después de que k pasa por la matriz, los primeros elementos k se ordenan. Sin embargo, la diferencia fundamental entre los dos algoritmos es que la ordenación por inserción explora hacia atrás desde la clave actual, mientras que la ordenación por selección explora hacia adelante. Esto da como resultado una ordenación por selección que convierte a los primeros k elementos en los k elementos más pequeños de la entrada no ordenada, mientras que en la ordenación por inserción son simplemente los primeros k elementos de la entrada.

La principal ventaja de la ordenación por inserción sobre la ordenación por selección es que la ordenación por selección siempre debe escanear todos los elementos restantes para encontrar el elemento más pequeño absoluto en la parte no ordenada de la lista, mientras que la ordenación por inserción requiere solo una única comparación cuando ( k + 1)-st elemento es mayor que k-th elemento; cuando esto es cierto con frecuencia (como si la matriz de entrada ya está ordenada o parcialmente ordenada), la ordenación por inserción es claramente más eficiente en comparación con la ordenación por selección. En promedio (asumiendo que el rango del elemento (k + 1)-st es aleatorio), la ordenación por inserción requerirá comparar y cambiar la mitad de los elementos k anteriores, lo que significa esa ordenación por inserción realizará aproximadamente la mitad de comparaciones que la ordenación por selección en promedio.

En el peor de los casos de ordenación por inserción (cuando la matriz de entrada se ordena de forma inversa), la ordenación por inserción realiza tantas comparaciones como la ordenación por selección. Sin embargo, una desventaja de la ordenación por inserción sobre la ordenación por selección es que requiere más escrituras debido al hecho de que, en cada iteración, al insertar el elemento (k + 1)-st en la parte ordenada de la matriz requiere muchos intercambios de elementos para cambiar todos los siguientes elementos, mientras que solo se requiere un solo intercambio para cada iteración del tipo de selección. En general, la ordenación por inserción escribirá en la matriz O(n²) veces, mientras que la ordenación por selección escribirá solo O( $n$ ) veces. Por esta razón, la ordenación por selección puede ser preferible en los casos en que escribir en la memoria es significativamente más costoso que leer, como con EEPROM o memoria flash.

Mientras que algunos algoritmos divide y vencerás, como la ordenación rápida y la ordenación por fusión, superan la ordenación por inserción en matrices más grandes, los algoritmos de ordenación no recursiva, como la ordenación por inserción o la ordenación por selección, son generalmente más rápidos para matrices muy pequeñas (el tamaño exacto varía según el entorno y implementación, pero normalmente tiene entre 7 y 50 elementos). Por lo tanto, una optimización útil en la implementación de esos algoritmos es un enfoque híbrido, utilizando el algoritmo más simple cuando la matriz se ha dividido en un tamaño pequeño.

`Variantes`

D. L. Shell realizó mejoras sustanciales en el algoritmo; la versión modificada se llama Shell sort. El algoritmo de clasificación compara elementos separados por una distancia que disminuye en cada pasada. Shell sort ha mejorado claramente los tiempos de ejecución en el trabajo práctico, con dos variantes simples que requieren O(n^3/2) y O(n^4/3) tiempo de ejecución.

Si el costo de las comparaciones excede el costo de los intercambios, como es el caso, por ejemplo, con claves de cadena almacenadas por referencia o con interacción humana (como elegir uno de un par que se muestra uno al lado del otro), entonces usando la ordenación por inserción binaria puede generar un mejor rendimiento. La ordenación por inserción binaria emplea una búsqueda binaria para determinar la ubicación correcta para insertar nuevos elementos y, por lo tanto, realiza comparaciones ⌈log₂ n⌉ en el peor de los casos. Cuando se busca e inserta cada elemento en la matriz, este es O(n log n). El algoritmo en su conjunto todavía tiene un tiempo de ejecución de O(n²) en promedio debido a la serie de intercambios necesarios para cada inserción.

La cantidad de intercambios se puede reducir calculando la posición de varios elementos antes de moverlos. Por ejemplo, si la posición de destino de dos elementos se calcula antes de que se muevan a la posición adecuada, la cantidad de intercambios se puede reducir en aproximadamente un 25 % para datos aleatorios. En el caso extremo, esta variante funciona de manera similar a la ordenación por fusión.

Una variante denominada clasificación por combinación binaria utiliza una clasificación por inserción binaria para clasificar grupos de 32 elementos, seguida de una clasificación final mediante la clasificación por fusión. Combina la velocidad de clasificación por inserción en conjuntos de datos pequeños con la velocidad de clasificación por fusión en conjuntos de datos grandes.

Para evitar tener que hacer una serie de intercambios para cada inserción, la entrada podría almacenarse en una lista enlazada, lo que permite que los elementos se empalmen dentro o fuera de la lista en tiempo constante cuando se conoce la posición en la lista. Sin embargo, buscar en una lista enlazada requiere seguir secuencialmente los enlaces hasta la posición deseada: una lista enlazada no tiene acceso aleatorio, por lo que no puede usar un método más rápido como la búsqueda binaria. Por lo tanto, el tiempo de ejecución requerido para buscar es O(n), y el tiempo para clasificar es O(n²). Si se utiliza una estructura de datos más sofisticada (p. ej., montón o árbol binario), el tiempo necesario para la búsqueda y la inserción se puede reducir significativamente; esta es la esencia de la ordenación en montón y la ordenación en árbol binario.

En 2006, Bender, Martin Farach-Colton y Mosteiro publicaron una nueva variante de clasificación por inserción denominada clasificación por biblioteca o clasificación por inserción con huecos que deja una pequeña cantidad de espacios sin usar (es decir, "brechas") repartidas por toda la matriz. El beneficio es que las inserciones solo necesitan cambiar elementos hasta que se alcanza un espacio. Los autores muestran que este algoritmo de clasificación se ejecuta con alta probabilidad en tiempo O(n log n).

Si se usa una lista de exclusión, el tiempo de inserción se reduce a O(log n) y no se necesitan intercambios porque la lista de exclusión se implementa en una estructura de lista vinculada. El tiempo de ejecución final para la inserción sería O(n log n).

`Lista de código de clasificación de inserción en C`

Si los elementos se almacenan en una lista vinculada, la lista se puede ordenar con O(1) espacio adicional. El algoritmo comienza con una lista inicialmente vacía (y por lo tanto ordenada trivialmente). Los elementos de entrada se eliminan de la lista de uno en uno y luego se insertan en el lugar adecuado en la lista ordenada. Cuando la lista de entrada está vacía, la lista ordenada tiene el resultado deseado.

struct LISTA * SortList1()struct LISTA * p Lista) {} // cero o un elemento en la lista si ()p Lista == NULL Silencio p Lista-pSiguiente == NULL) retorno p Lista; // la cabeza es el primer elemento de la lista clasificada resultante struct LISTA * cabeza = NULL; mientras ()p Lista ! NULL) {} struct LISTA * corriente = p Lista; p Lista = p Lista-pSiguiente; si ()cabeza == NULL Silencio corriente-iValue . cabeza-iValue) {} // insertar en el jefe de la lista ordenada // o como el primer elemento en una lista ordenada vacía corriente-pSiguiente = cabeza; cabeza = corriente; } más {} // insertar el elemento actual en la posición adecuada en la lista clasificada no vacía struct LISTA * p = cabeza; mientras ()p ! NULL) {} si ()p-pSiguiente == NULL Silencio // último elemento de la lista clasificada corriente-iValue . p-pSiguiente-iValue) // mitad de la lista {} // insertar en el centro de la lista ordenada o como el último elemento corriente-pSiguiente = p-pSiguiente; p-pSiguiente = corriente; descanso; // } p = p-pSiguiente; } } } retorno cabeza;}

El siguiente algoritmo utiliza un puntero final para la inserción en la lista ordenada. Un método recursivo más simple reconstruye la lista cada vez (en lugar de empalmar) y puede usar el espacio de pila O(n).

struct LISTA{} struct LISTA * pSiguiente; int iValue;};struct LISTA * SortList()struct LISTA * p Lista){} // cero o un elemento en la lista si ()!p Lista Silencio !p Lista-pSiguiente) retorno p Lista; /* construir la matriz ordenada de la lista vacía */ struct LISTA * pSorted = NULL; /* sacar elementos de la lista de entrada uno por uno hasta vacío */ mientras ()p Lista ! NULL) {} *Recuerda la cabeza */ struct LISTA * p Head = p Lista; /* puntero de seguimiento para empalme eficiente */ struct LISTA # ppTrail = "pSorted; /* pop head off list */ p Lista = p Lista-pSiguiente; /* Cabeza de empalme en lista clasificada en el lugar adecuado */ mientras ()!()*ppTrail == NULL Silencio p Head-iValue . ()*ppTrail)-iValue) {} ¿La cabeza pertenece aquí? */ /* no - continuar abajo la lista */ ppTrail = "()*ppTrail)-pSiguiente; } p Head-pSiguiente = *ppTrail; *ppTrail = p Head; } retorno pSorted;}

`Contenido relacionado`

MPEG-2
Búsqueda lineal
IRQ
 Más resultados... 
Te puede interesar