Tetraedro truncado

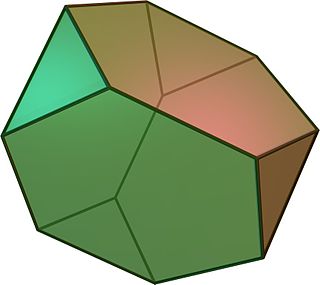
En geometría, el tetraedro truncado es un sólido de Arquímedes. Tiene 4 caras hexagonales regulares, 4 caras de triángulos equiláteros, 12 vértices y 18 aristas (de dos tipos). Se puede construir truncando los 4 vértices de un tetraedro regular a un tercio de la longitud de la arista original.
Un truncamiento más profundo, que elimina un tetraedro de la mitad de la longitud de la arista original de cada vértice, se denomina rectificación. La rectificación de un tetraedro produce un octaedro.
Un tetraedro truncado es el poliedro de Goldberg GIII(1,1), que contiene caras triangulares y hexagonales.
A truncated tetrahedron se puede llamar cubeta, con el diagrama de Coxeter, ![]()
![]()
![]()
![]()
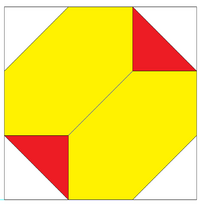
![]() , teniendo la mitad de los vértices del cubo (rhombicuboctaedro),
, teniendo la mitad de los vértices del cubo (rhombicuboctaedro), ![]()
![]()
![]()
![]()
![]() . Hay dos posiciones duales de esta construcción, y combinarlas crea el compuesto uniforme de dos tetrahedra truncada.
. Hay dos posiciones duales de esta construcción, y combinarlas crea el compuesto uniforme de dos tetrahedra truncada.
Área y volumen
El área A y el volumen V de un tetraedro truncado de longitud de arista a son:
- A=73a2.. 12.12435565a2V=23122a3.. 2.710575995a3.{displaystyle {begin{aligned}A limit=7{sqrt {3}a}a^{2} {2} {2}\cH00} {23}{12}}{sqrt {2} {2}a} {3} {3} {3} {3} {3} {3}} {3}} {3}} {}} {}}}} {}}}}a} {3} {3}} {}}}}a} {}} {}}}}}}}a}}a} {}}}}} {}}}} {}}}}}}}a} {}}} {}}}} {}}}}}}}a} {}}}a}a}a} {}}} {}}}}}}}}}} {}}}}}}}}}a}a} {} {}}}}a}a} {}}}}}}}}}}}}}}a}}}}}} {}}}}}a}}}}a} {}}}}}}}}}}}}}}}}
Embalaje más denso
Se cree que el empaquetamiento más denso del tetraedro truncado de Arquímedes es Φ = 207/208, según lo informado por dos grupos independientes que utilizan métodos de Monte Carlo. Aunque no existe ninguna prueba matemática de que este sea el mejor empaquetamiento posible para el tetraedro truncado, la gran proximidad a la unidad y la independencia de los hallazgos hacen que sea poco probable que se encuentre un empaquetamiento aún más denso. De hecho, si el truncamiento de las esquinas es ligeramente más pequeño que el de un tetraedro truncado de Arquímedes, esta nueva forma se puede utilizar para llenar completamente el espacio.
Coordenadas cartesianas
Las coordenadas cartesianas de los 12 vértices de un tetraedro truncado centrado en el origen, con una longitud de arista √8, son todas permutaciones de (±1,±1,±3) con un número par de signos menos:
- (+3,+1,+1), (+1,+3,+1), (+1,+1,+3)
- (3,−1,+1), (−1,−3,+1), (−1,−1,+3)
- (3,–1,–1), (–1,+3,–1), (–1,–1,–3)
- (+3,–1,–1), (+1,–3,–1), (+1,–1,–3)
Existe otra construcción simple en el espacio de 4 como celdas de las 16 celdas truncadas, con vértices como permutación de coordenadas de:
- (0,0,1,2)
Proyección ortogonal
| Centrado por | Edge normal | Cara normal | Edge | Cara |
|---|---|---|---|---|
| Wireframe |  |  |   | |
| Wireframe |  |  |  |  |
| Doble |  |  |  |  |
| Projective simetría | [1] | [1] | [4] | [3] |
Alicatados esféricos
El tetraedro truncado también puede representarse como un mosaico esférico y proyectarse en el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando ángulos pero no áreas o longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.
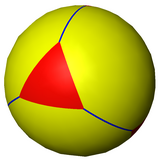 |  triángulo centrado |  hexágono centrado | |
| Proyección ortográfica | Proyecciones estereográficas | ||
|---|---|---|---|
Poliedro de Friauf
Una versión de menor simetría del tetraedro truncado (un disfenoide tetragonal truncado con simetría de orden 8 D2d) se denomina poliedro de Friauf en cristales como aleaciones metálicas complejas. Esta forma ajusta 5 poliedros de Friauf alrededor de un eje, dando un ángulo diedro de 72 grados en un subconjunto de 6-6 aristas. Lleva el nombre de J. B. Friauf y su artículo de 1927 "La estructura cristalina del compuesto intermetálico MgCu2".
Usos
Se utilizaron tetraedros truncados gigantes para el "Man the Explorer" y "Man the Producer" pabellones temáticos en la Expo 67. Estaban hechos de enormes vigas de acero atornilladas juntas en una celosía geométrica. Los tetraedros truncados estaban interconectados con plataformas de celosía de acero. Todos estos edificios fueron demolidos después del final de la Expo 67, ya que no se habían construido para soportar la severidad del clima de Montreal a lo largo de los años. Sus únicos restos se encuentran en los archivos de la ciudad de Montreal, los Archivos Públicos de Canadá y las colecciones de fotografías de turistas de la época.
Did you mean:The Teraminx puzzle has a truncated tetrahedral shape. This puzzle shows a dissection of a truncated tetrahedron into 4 octahedron and 6 tetrahedra. It contains 4 central planes of rotations.
Gráfico tetraédrico truncado
En el campo matemático de la teoría de grafos, un gráfico tetraédrico truncado es un gráfico de Arquímedes, el gráfico de vértices y aristas del tetraedro truncado, uno de los sólidos de Arquímedes. Tiene 12 vértices y 18 aristas. Es un gráfico cúbico conexo y un gráfico transitivo cúbico conexo.
| Circular |
|---|
 |
| Proyecciones ortoográficas | |
|---|---|
 Simetría 4 veces |  Simetría 3 veces |
Poliedros y mosaicos relacionados
También forma parte de una secuencia de poliedros cánticos y teselas con configuración de vértice 3.6.n.6. En esta construcción de Wythoff, los bordes entre los hexágonos representan digons degenerados.
Mutaciones de simetría
Este poliedro está relacionado topológicamente como parte de una secuencia de poliedros truncados uniformes con configuraciones de vértice (3.2n.2n) y [n,3] Simetría del grupo de Coxeter.
Ejemplos
dibujo en De divina proporcionae (1509)
dibujo en Perspectiva Corporum Regularium (1568)
modelo de cristal
fotos desde diferentes perspectivas (Matemateca)
Muerto de 4 caras
12 permutaciones de ()4,2,0,0){displaystyle (4,2,0,0)} (brown)
Contenido relacionado
Leopoldo Vietoris
Número aleatorio
Magnitud