Tetradecágono
En geometría, un tetradecágono o tetracaidecágono o 14-ágono es un polígono de catorce lados.
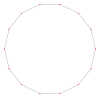
Tetradecagon regular
Un tetradecágono regular tiene el símbolo de Schläfli {14} y puede construirse como un heptágono truncado cuasirregular, t{7}, que alterna dos tipos de aristas.
El área de un tetradecágono regular de lado a está dada por
Construcción
Como 14 = 2 × 7, no se puede construir un tetradecágono regular con compás y regla. Sin embargo, sí se puede construir con neusis utilizando el trisector de ángulos o con una regla marcada, como se muestra en los dos ejemplos siguientes.

Una animación (1 min 47 s) de una construcción de neusis con radio de circuncircle ,
según Andrew M. Gleason, basado en la trisección de ángulo por medio del tomahawk.

Una animación (1 min 20 s) de una construcción de neusis con marcador, según David Johnson Leisk (Crockett Johnson).
Simmetría

El tetradecágono regular tiene simetría Dih14, orden 28. Hay 3 simetrías diedras de subgrupos: Dih7, Dih2 y Dih1, y 4 simetrías de grupos cíclicos: Z14, Z7, Z2 y Z1.
Estas 8 simetrías se pueden ver en 10 simetrías distintas en el tetradecágono, un número mayor porque las líneas de reflexión pueden pasar por vértices o aristas. John Conway las etiqueta con una letra y un orden de grupo. La simetría completa de la forma regular es r28 y ninguna simetría se etiqueta como a1. Las simetrías diedricas se dividen según si pasan por vértices (d para diagonales) o aristas (p para perpendiculares), e i cuando las líneas de reflexión pasan por aristas y vértices. Las simetrías cíclicas en la columna del medio se etiquetan como g para sus órdenes de giro centrales.
La simetría de cada subgrupo permite uno o más grados de libertad para las formas irregulares. Sólo el subgrupo g14 no tiene grados de libertad, pero puede verse como aristas dirigidas.
Los tetradecágonos irregulares de mayor simetría son d14, un tetradecágono isogonal construido con siete espejos que pueden alternar aristas largas y cortas, y p14, un tetradecágono isotoxal, construido con aristas de igual longitud, pero vértices que alternan dos ángulos internos diferentes. Estas dos formas son duales entre sí y tienen la mitad del orden de simetría del tetradecágono regular.
Disección
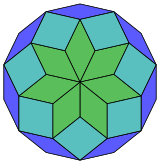
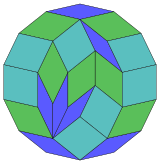
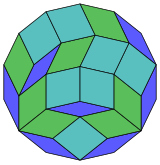
 Proyección de 14 cachorros |  84 romb disección |
Coxeter afirma que todo zonógono (un 2m-gono cuyos lados opuestos son paralelos y de igual longitud) puede diseccionarse en m(m-1)/2 paralelogramos. En particular, esto es cierto para polígonos regulares con un número uniforme de lados, en cuyo caso los paralelogramos son todos rombos. Para el tetradecágono regular, m=7, y puede dividirse en 21: 3 conjuntos de 7 rombos. Esta descomposición se basa en una proyección poligonal de Petrie de un 7-cubo, con 21 de 672 caras. La lista OEIS: A006245 define el número de soluciones como 24698, incluidas rotaciones de hasta 14 pliegues y formas quirales en reflexión.
 |  |  |  |  |  |
Uso numérico
El tetradecágono regular se utiliza como forma de algunas monedas conmemorativas de oro y plata de Malasia, y el número de caras representa los 14 estados de la Federación de Malasia.
Cifras relacionadas

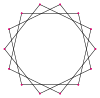
Un tetradecagrama es un polígono estrellado de 14 lados, representado por el símbolo {14/n}. Hay dos polígonos estrellados regulares: {14/3} y {14/5}, que utilizan los mismos vértices, pero que conectan cada tercer o quinto punto. También hay tres compuestos: {14/2} se reduce a 2{7} como dos heptágonos, mientras que {14/4} y {14/6} se reducen a 2{7/2} y 2{7/3} como dos heptagramas diferentes, y finalmente {14/7} se reduce a siete dígonos.
Una aplicación notable de la estrella de catorce puntas se encuentra en la bandera de Malasia, que incorpora un tetradecagrama amarillo {14/6} en la esquina superior derecha, que representa la unidad de los trece estados con el gobierno federal.
Los truncamientos más profundos del heptágono regular y de los heptagramas pueden producir formas de tetradecagramas intermedios isogonales (transitivos de vértice) con vértices igualmente espaciados y dos longitudes de arista. Otros truncamientos pueden formar polígonos de doble recubrimiento 2{p/q}, a saber: t{7/6}={14/6}=2{7/3}, t{7/4}={14/4}=2{7/2} y t{7/2}={14/2}=2{7}.
| truncaciones de heptógono y heptagramas | ||||
|---|---|---|---|---|
| Quasiregular | Isogonal | Quasiregular Cubierta doble | ||
 t{7}={14} | 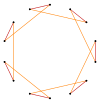 | 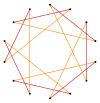 |  |  {7/6}={14/6} =2{7/3} |
 t{7/3}={14/3} |  |  | 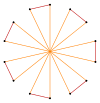 |  t{7/4}={14/4} =2{7/2} |
 t{7/5}={14/5} |  | 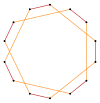 |  |  t{7/2}={14/2} =2{7} |
Formas Isotoxales
Un polígono isotoxal puede etiquetarse como {pα} con el ángulo interno más externo α, y un polígono en estrella {(p/q)α}, con q como un número sinuoso y mcd(p,q)=1, q<p. Los tetradecágonos isotoxales tienen p=7, y como 7 es primo, todas las soluciones, q=1..6, son polígonos.
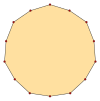 {7α} | 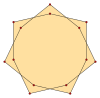 [(7/2)α} |  {(7/3)α} | 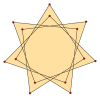 {(7/4)α} |  {(7/5)α} | 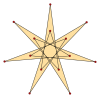 [(7/6)α} |
Petrie poligons
Los tetradecágonos oblicuos regulares existen como polígonos de Petrie para muchos politopos de dimensiones superiores, que se muestran en estas proyecciones ortogonales oblicuas, entre ellas:
| Petrie poligons | ||||
|---|---|---|---|---|
| B7 | 2I2(7) (4D) | |||
 7-orthoplex |  7-cube | 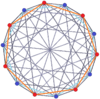 7-7 duopyramid |  7-7 duoprismo | |
| A13 | D8 | E8 | ||
 13-simplex | 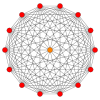 511 |  151 | 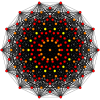 421 |  241 |
Referencias
- ^ Wantzel, Pierre (1837). "Recherches sur les moyens de Reconnaître si un Problème de géométrie peau se résoudre avec la règle et le compas" (PDF). Journal de Mathématiques: 366–372.
- ^ a b Gleason, Andrew Mattei (marzo de 1988). "La trisección águila, el heptógono, p. 186 (Fig.1) –187" (PDF). American Mathematical Monthly. 95 (3): 185–194. doi:10.2307/2323624. Archivado desde el original (PDF) on 2016-02-02.
- ^ a b Weisstein, Eric W. "Heptagon". De MathWorld, A Wolfram Web Resource.
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (capítulo 20, Generalized Schaefli symbol, Types of symmetry of a polygon pp. 275-278)
- ^ Coxeter, recreaciones y ensayos matemáticos, 13a edición, p.141
- ^ El Numismatista, Volumen 96, Temas 7-12, Página 1409, American Numismatic Association, 1983.
- ^ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorfosis de polígonos, Branko Grünbaum
Enlaces externos
- Weisstein, Eric W. "Tetradecagon". MathWorld.