Teoría del elemento pala

Teoría del elemento Blade (BET) es un proceso matemático diseñado originalmente por William Froude (1878), David W. Taylor (1893) y Stefan Drzewiecki (1885) para Determinar el comportamiento de las hélices. Implica romper una pala en varias partes pequeñas y luego determinar las fuerzas sobre cada uno de estos pequeños elementos de la pala. Luego, estas fuerzas se integran a lo largo de toda la pala y a lo largo de una revolución del rotor para obtener las fuerzas y momentos producidos por toda la hélice o rotor. Una de las dificultades clave radica en modelar la velocidad inducida en el disco del rotor. Debido a esto, la teoría del elemento de pala a menudo se combina con la teoría del momento para proporcionar relaciones adicionales necesarias para describir la velocidad inducida en el disco del rotor, produciendo la teoría del momento del elemento de pala. En el nivel más básico de aproximación se supone una velocidad inducida uniforme en el disco:

${displaystyle {fnMicroc} {fnMicroc} {T}cdot {1}{2rho - Sí.$

Alternativamente, la variación de la velocidad inducida a lo largo del radio se puede modelar dividiendo la hoja en pequeños anillos y aplicando la conservación de masa, momento y energía a cada anillo. Este enfoque a veces se denomina ecuación de Froude-Finsterwalder.

Si el método del elemento de pala se aplica a rotores de helicópteros en vuelo hacia adelante, es necesario considerar el movimiento de aleteo de las palas, así como la distribución longitudinal y lateral de la velocidad inducida en el disco del rotor. Los modelos de flujo de entrada de vuelo directo más simples son los modelos de primeros armónicos.

Teoría simple del elemento pala

Si bien la teoría del momento es útil para determinar la eficiencia ideal, ofrece una descripción muy incompleta de la acción de las hélices de tornillo, ignorando, entre otras cosas, el par. Para investigar con mayor detalle el funcionamiento de la hélice, se considera que las palas están formadas por varios elementos pequeños y se calculan las fuerzas del aire sobre cada elemento. Así, mientras que la teoría del momento se ocupa del flujo de aire, la teoría del elemento de pala se ocupa principalmente de las fuerzas sobre las palas de la hélice. La idea de analizar las fuerzas sobre tiras elementales de palas de hélice fue publicada por primera vez por William Froude en 1878. Drzewiecki también la desarrolló de forma independiente y se presentó en un libro sobre vuelo mecánico publicado en Rusia siete años después, en 1885. De nuevo, en En 1907, Lanchester publicó una forma algo más avanzada de la teoría del elemento cuchilla sin conocimiento de trabajos previos sobre el tema. Sin embargo, la teoría simple del elemento cuchilla suele denominarse teoría de Drzewiecki, porque fue Drzewiecki quien la puso en forma práctica y la generalizó. Además, fue el primero en sumar las fuerzas sobre los elementos de las palas para obtener el empuje y el par de una hélice completa y el primero en introducir la idea de utilizar datos del perfil aerodinámico para encontrar las fuerzas sobre los elementos de las palas.

En la teoría del elemento de pala de Drzewiecki, la hélice se considera un perfil aerodinámico deformado o torcido, cada segmento del cual sigue una trayectoria helicoidal y se trata como un segmento de un ala ordinaria. Generalmente se supone en la teoría simple que los coeficientes de perfil aerodinámico obtenidos de pruebas en túnel de viento de alas de modelos (normalmente probadas con una relación de aspecto de 6) se aplican directamente a elementos de palas de hélice de la misma forma de sección transversal.

El flujo de aire alrededor de cada elemento se considera bidimensional y, por lo tanto, no se ve afectado por las partes adyacentes de la pala. La independencia de los elementos de la pala en cualquier radio dado con respecto a los elementos vecinos se ha establecido teóricamente y también se ha demostrado que es sustancialmente cierta para las secciones de trabajo de la pala mediante experimentos especiales realizados para este propósito. También se supone que el aire pasa a través de la hélice sin flujo radial (es decir, no hay contracción del rebufo al pasar a través del disco de la hélice) y que no hay interferencia de las palas.

Fuerzas aerodinámicas sobre un elemento de pala

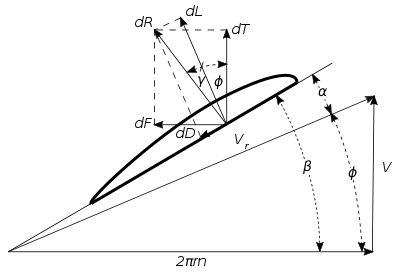
Considerar el elemento en radio r, mostrado en la Fig. 1, que tiene la longitud infinitesimal ♪ y el ancho b. El movimiento del elemento en una hélice en vuelo es a lo largo de un camino helicoidal determinado por la velocidad de avance V de la aeronave y la velocidad tangencial 2πrn del elemento en el plano del disco de hélice, donde n representa las revoluciones por unidad de tiempo. La velocidad del elemento con respecto al aire Vr es entonces el resultado de las velocidades hacia adelante y tangencial, como se muestra en Fig. 2. Llamar el ángulo entre la dirección del movimiento del elemento y el plano de rotación ⋅, y el ángulo de la hoja β. El ángulo de ataque α del elemento relativo al aire es entonces ${displaystyle alpha =beta -.$.

Aplicando coeficientes ordinarios de perfil aerodinámico, la fuerza de sustentación sobre el elemento es:

${displaystyle DL={frac {1}{2}V_{2}C_{L}b,dr.}$

Vamos γ ser el ángulo entre el componente de elevación y la fuerza resultante, o ${textstyle gamma =arctan {frac {} {}}}$. Entonces la fuerza aérea total resultante en el elemento es:

$${displaystyle DR={frac {frac {1}{2}V_{2}C_{L}b,dr}{cos gamma }}}$$

El empuje del elemento es el componente de la fuerza resultante en la dirección del eje de la hélice (Fig. 2), o

$${displaystyle {begin{aligned}dT limit=dRcos(phi +gamma)\\fnMicroc {frac} {1}{2}V_{2}C_{L}bcos(phi +gamma)}{cos gamma }dr,end{aligned}}}$$

${textstyle V_{}={frac} {V}{sin phi }$

$${displaystyle dT={frac} {1}{2}V^{2}C_{L}bcos(phi +gamma)}{sin ^{2}phi cos gamma }dr.}$$

Para mayor comodidad, deje

$${displaystyle K={frac {C_{L}b}{2}ficos gamma }$$

$${displaystyle T_{c}=Kcos(phi +gamma).}$$

Entonces

$${displaystyle dT={}{2}rho V^{2}T_{c},dr,}$$

$${displaystyle T={2}rho V^{2}Bint ¿Qué?$$

Refiriéndose nuevamente a la Fig. 2, la fuerza tangencial o de torsión es

${displaystyle dF=dRsin(phi +gamma),}$

y el torque sobre el elemento es

${displaystyle dQ=r,dR,sin(phi +gamma),}$

que, si ${textstyle Q_{c}=Krsin(phi +gamma)}$, puede ser escrito

${displaystyle dQ={}{2}rho V^{2}Q_{c}dr.}$

Por lo tanto, la expresión para el par de toda la hélice es

${displaystyle Q={2}rho V^{2}Bint ¿Qué?$

La potencia absorbida por la hélice, o la potencia de torsión, es

${displaystyle QHP={frac {2pi nQ}{550}}$

y la eficiencia es

${displaystyle eta ={frac {THP}={frac {TV} {2pi nQ}}$

Eficiencia

Debido a la variación del ancho de la pala, el ángulo y la sección del perfil aerodinámico a lo largo de la pala, no es posible obtener una expresión simple para el empuje, el par y la eficiencia de las hélices en general. Sin embargo, un solo elemento situado aproximadamente a dos tercios o tres cuartos del radio de la punta es bastante representativo de toda la hélice y, por lo tanto, es interesante examinar la expresión de la eficiencia de un solo elemento. La eficiencia de un elemento es la relación entre la potencia útil y la potencia absorbida, o

${displaystyle {begin{aligned}eta " {frac {dTV}{dQ2pi n}\\fn}\fnMicroc {dRcos(phi +gamma)V}{dRsin(phi +gamma)2pi nr}\fr={frac {tan phi }{tan(phi +gamma)}}end{aligned}}}}}}} {fn0}} {fnMinun}}}} {fnun}}}}}}}}}}}}fnunfnunfnunfnun}fnunfnunfnunfnunfnunfnunfnunfnunfnunfnunfnunfnunfnunfnunfnunfnunfnun}}fnun}}fnun}}}fnun {fnunfnunfnun}fnun}}}nunfnun}}}fnun}}}}}$

Ahora bronceado CCPR es la relación del futuro con la velocidad tangencial, y ${textstyle tan gamma ={frac {} {}}}$. De acuerdo con la simple teoría del elemento de la hoja, por lo tanto, la eficiencia de un elemento de la hélice depende sólo de la relación del futuro con la velocidad tangencial y de la ${textstyle {frac {} {}}}$ de la sección de airfoil.

El valor de Φ que da la máxima eficiencia para un elemento, como se encuentra diferenciando la eficiencia con respecto a Φ e igualando el resultado a cero, es

$${displaystyle phi =45^{circ }-{frac {gamma } {2}}$$

La variación de la eficiencia con 0 se muestra en la Fig. 3 para dos valores extremos de γ. La eficiencia aumenta a un máximo ${textstyle 45^{fnMicrosoft} }-{frac {gamma } {2}}$ y luego cae a cero de nuevo ${textstyle 90^{fnMicrosoft} }-gamma }$. Con una ${textstyle {frac {L}{D}}$ de 28.6 la máxima eficiencia posible de un elemento según la simple teoría es 0.932, mientras que con un ${textstyle {frac {L}{D}}$ de 9.5 es sólo 0.812. A los valores CCPR a los que trabajan los elementos más importantes de la mayoría de las hélices (10° a 15°) el efecto ${textstyle {frac {L}{D}}$ sobre la eficiencia sigue siendo mayor. Dentro del rango de 10° a 15°, las curvas en la Fig. 3 indican que es ventajoso tener ambas ${textstyle {frac {L}{D}}$ de las secciones de aire y el ángulo CCPR (o el avance por revolución, y por consiguiente el lanzamiento) lo más alto posible.

Limitaciones

Según la teoría del momento, se imparte una velocidad al aire que pasa a través de la hélice, y la mitad de esta velocidad se le da al aire cuando llega al plano de la hélice. Este aumento de velocidad del aire a medida que pasa hacia el disco de la hélice se denomina velocidad de entrada. Siempre se encuentra cuando hay discontinuidad de presión en un fluido. En el caso de un ala que se mueve horizontalmente, al aire se le da una velocidad hacia abajo, como se muestra en la Fig. 4, y teóricamente la mitad de esta velocidad se imparte delante y encima del ala, y la otra mitad debajo y detrás.

Este flujo descendente inducido está presente en las pruebas del modelo de ala a partir de las cuales se obtienen los coeficientes del perfil aerodinámico utilizados en la teoría del elemento de pala; Por lo tanto, el flujo de entrada indicado por la teoría del momento se tiene en cuenta automáticamente en la teoría simple del elemento de pala. Sin embargo, el flujo descendente inducido es muy diferente para diferentes relaciones de aspecto, siendo cero para relaciones de aspecto infinitas. La mayoría de las pruebas de modelos de perfiles aerodinámicos se realizan con alas rectangulares que tienen una relación de aspecto arbitrariamente elegida de 6, y no hay razón para suponer que el flujo descendente en tal prueba corresponda al flujo de entrada para cada elemento de una pala de hélice. De hecho, la conclusión general extraída de una serie exhaustiva de pruebas, en las que se midió la distribución de la presión en 12 secciones de un modelo de hélice que funciona en un túnel de viento, es que el coeficiente de sustentación del elemento de pala de la hélice difiere considerablemente del medido en el mismo ángulo de ataque en un perfil aerodinámico de relación de aspecto 6. Ésta es una de las mayores debilidades de la teoría simple del elemento de pala.

Otra debilidad es que no se considera la interferencia entre las palas de la hélice. Los elementos de las palas en cualquier radio particular forman una cascada similar a un multiplano con escalonamiento negativo, como se muestra en la Fig. 4. Cerca de las puntas, donde el espacio es grande, la interferencia es muy pequeña, pero hacia las raíces de las palas es bastante grande.

En las hélices reales hay una pérdida en la punta que la teoría del elemento de pala no tiene en cuenta. Las fuerzas de empuje y torsión calculadas mediante la teoría son, por tanto, mayores para los elementos cercanos a la punta que las encontradas experimentalmente.

Para eliminar el efecto de escala, las pruebas en el túnel de viento en alas de modelos deben realizarse con el mismo valor del número de Reynolds (escala) que los elementos correspondientes en las palas de la hélice. Características del perfil aerodinámico medidas a una escala tan baja como, por ejemplo, una velocidad del aire de 30 mph. con 3 pulgadas. perfil aerodinámico de cuerda, presentan peculiaridades que no se encuentran cuando las pruebas se realizan a una escala comparable a la de los elementos de hélice. Las características estándar de la sección de hélice dadas en las Figs. 11, 12, 13 y 14 se obtuvieron a partir de pruebas de alto número de Reynolds en el Túnel de Densidad Variable de la N.A.C.A. y, afortunadamente, para todas, excepto la más gruesa de estas secciones, hay muy poca diferencia en las características con números de Reynolds altos y bajos.. Estos valores pueden usarse con una precisión razonable en cuanto a escala para hélices que funcionan a velocidades punta muy por debajo de la velocidad del sonido en el aire y, por lo tanto, relativamente libres de cualquier efecto de compresibilidad.

La escasa precisión de la teoría simple del elemento de pala se muestra muy bien en un informe de Durand y Lesley, en el que calcularon el rendimiento de un gran número de modelos de hélices (80) y compararon los valores calculados con los rendimientos reales obtenidos de pruebas en las propias hélices del modelo. En palabras de los autores:

Las divergencias entre los dos conjuntos de resultados, al tiempo que muestran ciertos elementos de consistencia, son demasiado grandes y demasiado caprichosamente distribuidas para justificar el uso de la teoría en esta forma más simple para otras estimaciones aproximadas o para fines comparativos.

Los perfiles se probaron en dos túneles de viento diferentes y en uno de los túneles a dos velocidades de aire diferentes, y las características de la hélice calculadas a partir de los tres conjuntos de datos de los perfiles difieren hasta en un 28%, lo que ilustra claramente la necesidad de realizar las pruebas de perfil aerodinámico a la escala correcta.

A pesar de todas sus imprecisiones, la teoría simple de los elementos de pala ha sido una herramienta útil en manos de diseñadores de hélices experimentados. Con él, un diseñador hábil que tenga conocimiento de los factores empíricos adecuados puede diseñar hélices que generalmente se ajustan bastante bien a las condiciones principales que se les imponen, ya que absorben la potencia del motor a una velocidad de revolución muy cercana a la adecuada. Sin embargo, no son necesariamente las hélices más eficientes para su propósito, ya que la teoría simple no es lo suficientemente precisa como para mostrar ligeras diferencias en eficiencia debido a cambios en la distribución del paso, las formas de la planta, etc.

Ejemplo

Al elegir una hélice para analizar, es deseable que se conozcan sus características aerodinámicas para poder comprobar la exactitud de los resultados calculados. También es deseable que el análisis se haga de una hélice que funciona a una velocidad punta relativamente baja para estar libre de cualquier efecto de compresibilidad y que funcione sin interferencias del cuerpo. Las únicas pruebas de hélices que cumplen todas estas condiciones son las pruebas de modelos de hélices en un túnel de viento. Por lo tanto, tomaremos como ejemplo la hélice central o maestra de una serie de modelos de hélices de madera de forma estándar de la Marina, probadas por el Dr. W. F. Durand en la Universidad de Stanford. Se trata de una hélice de dos palas de 3 pies de diámetro, con un paso geométrico uniforme de 2,1 pies (o una relación paso-diámetro de 0,7). Las palas tienen secciones de hélice estándar basadas en el perfil aerodinámico R.A.F-6 (Fig. 6), y los anchos, espesores y ángulos de las palas son los indicados en la primera parte de la Tabla I. En nuestro análisis consideraremos que la hélice avanza con una velocidad de 40 mph. y girando a un ritmo de 1.800 r.p.m.

Para la sección al 75% del radio de la punta, el radio es 1,125 pies, el ancho de la hoja es 0,198 pies, la relación de espesor es 0,107, la curvatura inferior es cero y el ángulo de la hoja β es 16,6°.

La velocidad de avance

$${displaystyle {begin{aligned}Viéndose=40mathrm {m.p.h.}\ccc {40times 88}{60}\\\\\\cH009\\fnMicrosoft Sans Serif},end{aligned}}}}}}}}}}}\\\\\\\fnMinMicronMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMin.$$

y

$${displaystyle {begin{aligned {frac {1800}\\\\\\fnMicrosoft Sans Serif}}}end{aligned}}}}} {fnMicrosoft Sans Serif}$$

El ángulo del camino

${displaystyle {begin{aligned}phis {fnMicrosoft Sans Serif}\\fnMicroc {58.65}{2pitimes 1.125times 30}\\\\\\cH00\\\cH55\cH00}\cH00\\cH55\cH55cH009\\cH3nMicrox9}}fnMicrob9}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\cH00\\cH$

El ángulo de ataque es por lo tanto

${displaystyle {begin{aligned}alpha..... \c=16.6^{circ }-15.5^{circ }\\end{aligned}}$

De la Fig. 7, para una sección de cara plana con una relación de espesor de 0,107 en un ángulo de ataque de 1,1°, γ = 3,0° y, de la Fig. 9, C _L = 0,425. (Para secciones que tienen una curvatura inferior, C_L debe corregirse de acuerdo con la relación dada en la Fig. 8, y γ recibe la misma valor igual al de una sección de cara plana que tiene únicamente la curvatura superior.)

Entonces

${displaystyle {begin{aligned}K limit={frac {C_{l}b}{2}ficos gamma }\fnMicroc {0.425times 0.198}{0.2672^{2}times 0.999}\=1.180,end{aligned}}$

y,

${displaystyle {begin{aligned}T_{C} limit=Kcos(phi +gamma)\\\=1.180times cos 18.5^{circ }\\1.119.end{aligned}}$

Además,

${displaystyle {begin{aligned}Q_{C} distantes=Krsin(phi +gamma)\\\fn1times 1.125times sin 18.5^{circ }\=1.421.end{aligned}}}}}}$

Los cálculos de T_c y Q_c para seis elementos representativos de la hélice se dan en una conveniente forma tabular en la Tabla I, y los valores de T_c y Q_c se representan frente al radio en la Fig. 9. Las curvas dibujadas a través de estos puntos a veces se denominan curvas graduadas de torsión. Las áreas bajo la curva representan

$${displaystyle int ¿Qué?$$

$${displaystyle int ¿Qué?$$

Al utilizar la regla de Simpson, el radio se divide en un número par de partes iguales, como diez. La ordenada en cada división se puede encontrar a partir de la curva de calificaciones. Si los elementos originales de la pala dividen la pala en un número par de partes iguales, no es necesario trazar las curvas de nivelación, pero las curvas son ventajosas porque muestran gráficamente la distribución del empuje y el par a lo largo de la pala. También proporcionan una verificación de los cálculos, ya que los puntos incorrectos generalmente no formarán una curva justa.

Table I. — Computations for Propeller Analysis with Simple Blade- element Theory

D = 3.0 ft. p = 2.1 ft.	Forward velocity = 40 m.p.h. = 58.65 ft. /sec. Rotational velocity = 1,800 r.p.m. = 30 r.p.s.
r/R	0.15	0.30	0.45	0.60	0.75	0.90
r (ft.)	0.225	0.450	0.675	0.900	1.125	1.350
b (ft.)	0.225	0.236	0.250	0.236	0.198	0.135
hv/b	0.190	0.200	0.167	0.133	0.107	0.090
hl/b	0.180	0.058	0.007	000	000	000
β(deg.)	56.1	36.6	26.4	20.4	16.6	13.9
2πrn	42.3	84.7	127.1	169.6	212.0	254.0
${textstyle tan phi ={frac {V}{2pi rn}}}$	1.389	0.693	0.461	0.346	0.277	0.231
Φ (deg.)	54.2	34.7	24.7	19.1	15.5	13.0
${displaystyle alpha =beta -phi mathrm {(deg.)} }$	1.9	1.9	1.7	1.3	1.1	0.9
γ (deg.)	3.9	4.1	3.6	3.3	3.0	3.0
${displaystyle cos gamma }$	0.998	0.997	0.998	0.998	0.999	0.999
CL	0.084	0.445	0.588	0.514	0.425	0.356
sin Φ	0.8111	0.5693	0.4179	0.3272	0.2672	0.2250
${textstyle K={frac {C_{L}b}{cos gamma sin ^{2}phi }}}$	0.0288	0.325	0.843	1.135	1.180	0.949
Φ+γ (deg.)	58.1	38.8	28.3	22.4	18.5	16.0
cos(γ+Φ)	0.5280	0.7793	0.8805	0.9245	0.9483	0.9613
${textstyle T_{c}=Kcos(gamma +phi)}$	0.0152	0.253	0.742	1.050	1.119	0.912
sin(γ+Φ)	0.8490	0.6266	0.4741	0.3811	0.3173	0.2756
${textstyle Q_{c}=Krsin(gamma +phi)}$	0.0055	0.0916	0.270	0.389	0.421	0.353

Si las abscisas se denotan por r y las ordenadas en las distintas divisiones por y₁, y ₂,..., y₁₁, según la regla de Simpson el área con diez divisiones iguales será

$${displaystyle int _{0} {R}F(r),dr={frac {Delta r}{3}[y_{1}+2(y_{3}+y_{5}+y_{7}+y_{9})+4(y_{2}+y_{4}+y_{6}+y_{8}+y_{10})+y_{11}]}$$

Por lo tanto, el área bajo la curva de empuje de nuestro ejemplo es

${displaystyle {begin{aligned}in ¿Qué? {0.15}{3}}[0+2(0.038+0.600+1.050+1.091)+4(0+0.253+0.863+0.8120+0912)+0]\ punto=0.9075,end{aligned}}}}}$

y de la misma manera

$${displaystyle int ¿Qué?$$

Las integraciones anteriores también se han realizado mediante un planímetro, y los resultados promedio de cinco ensayos concuerdan con los obtenidos mediante la regla de Simpson dentro de un cuarto del uno por ciento.

El empuje de la hélice en aire estándar es

${displaystyle {begin{aligned}T ventaja={frac {1}{2}rho V^{2}Bint ¿Por qué? {1}{2}times 0.002378times 58.65^{2}times 2times 0.9075\\=7.42 mathrm {lb.}end{aligned}}}$

y el torque es

${displaystyle {begin{aligned}Q limit={frac {1}{2}rho V^{2}Bint ¿Por qué? {1}{2}times 0.002378times 58.65^{2}times 2times 0,340\=2.78\mathrm {lb.ft.}end{aligned}}}}$

La potencia absorbida por la hélice es

${displaystyle {begin{aligned}P ventaja=2pi nQ\\fnMis times 30times 2.78\\\\\\fnMicrosoft Sans Serif}.end{aligned}}}}}}}}$

o

${displaystyle {begin{aligned}HP ventaja={frac} {524}{550}\\=0.953,end{aligned}}$

y la eficiencia es

${displaystyle {begin{aligned}eta {fnMicrosoft Sans Serif}\\fnMicroc {7.42times 58.65}{524}}\\\\\\0.830.end{aligned}}}$

El rendimiento calculado anteriormente se compara con el medido en el túnel de viento de la siguiente manera:

La potencia calculada mediante la teoría simple del elemento de pala es en este caso más del 11 % demasiado baja, el empuje es aproximadamente un 5 % bajo y la eficiencia es aproximadamente un 8 % alta. Por supuesto, se habría obtenido un rendimiento calculado de manera diferente si se hubieran utilizado las características de la sección de la hélice de pruebas en la misma serie de perfiles aerodinámicos en un túnel de viento diferente, pero las pruebas en túneles de densidad variable son probablemente las más confiables de todas.

Se puede arrojar algo de luz sobre la discrepancia entre el rendimiento calculado y el observado consultando nuevamente las pruebas de distribución de presión en un modelo de hélice. En estas pruebas, se midió la distribución de presión en varias secciones de una pala de hélice mientras la hélice estaba funcionando en un túnel de viento, y se realizaron los tres conjuntos de pruebas siguientes en los perfiles aerodinámicos correspondientes:

Los resultados de estos tres conjuntos de pruebas de perfil aerodinámico se muestran para la sección en tres cuartos del radio de la punta en la Fig. 10, que se ha tomado del informe. Se observará que los coeficientes de la fuerza resultante C_R concuerdan bastante bien para la sección mediana del perfil aerodinámico de relación de aspecto 6 y la sección correspondiente de la pala de hélice especial. perfil aerodinámico, pero que el coeficiente de fuerza resultante para todo el perfil aerodinámico de relación de aspecto 6 es considerablemente menor. Es natural, entonces, que el empuje y la potencia calculados de una hélice sean demasiado bajos cuando se basan en las características del perfil aerodinámico para una relación de aspecto de 6.

Modificaciones

Se han sugerido muchas modificaciones a la teoría simple del elemento cuchilla para hacerla más completa y mejorar su precisión. La mayoría de estas teorías modificadas intentan tener en cuenta la interferencia de las palas y, en algunas de ellas, también se intenta eliminar la inexactitud debida al uso de datos del perfil aerodinámico de pruebas en alas que tienen una relación de aspecto finita, como 6. La primera modificación que se hizo fue una combinación de la teoría simple de Drzewiecki con la teoría del impulso de Froude.

Diagramas

• Secciones de hélice estándar basadas en la relación de aspecto infinito R.A.F.-6.
• 

  Fig 11.

• 

  Fig 12.

• 

  Gráfico 13

• 

  Gráfico 14

Atribución

Este artículo incorpora texto de esta fuente, que está en el dominio público: Weick, Fred Ernest (1899). Diseño de hélice de aeronaves. New York, McGraw-Hill Book Company, inc.