Teoría del caos

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Teoría del caos es una disciplina científica interdisciplinaria y una especialidad de las matemáticas. La teoría del caos estudia cómo pequeños cambios pueden causar grandes efectos en sistemas que parecen desordenados o aleatorios, pero que en realidad siguen patrones.

Así, se enfoca en los patrones y leyes deterministas que, aunque son altamente sensibles a las condiciones iniciales, subyacen (existen) en sistemas dinámicos que anteriormente se consideraban como meramente desordenados o aleatorios.

Esta teoría sostiene que, detrás de la aparente aleatoriedad de los sistemas caóticos, se esconden elementos como interconexiones, bucles de retroalimentación, repetición, autosimilitud, fractales y autoorganización. Un concepto clave es el efecto mariposa, que postula que un pequeño cambio en un sistema no lineal puede resultar en grandes variaciones en estados futuros (lo que significa que continúa una dependencia sensible de las condiciones iniciales). Esta idea se ilustra a menudo con la metáfora de que el simple aleteo de una mariposa en Brasil podría desencadenar un tornado en Texas.

Incluso pequeñas diferencias en las condiciones iniciales, ya sean por errores de medición o errores de redondeo numérico, pueden llevar a resultados altamente divergentes en sistemas dinámicos. Esto complica enormemente la predicción a largo plazo de su comportamiento.

A pesar de que estos sistemas son deterministas, es decir, su comportamiento futuro se determina completamente por sus condiciones iniciales sin intervención de elementos aleatorios, no garantiza su predictibilidad. En esencia, el ser determinista no los hace predecibles.

Este fenómeno se denomina caos determinista o simplemente caos. Edward Lorenz lo resumió diciendo:

Caos: Cuando el presente determina el futuro, pero el presente aproximado no determina aproximadamente el futuro.
Lorenz, Edward N. (1963).
"Deterministic non-periodic flow".
Journal of the Atmospheric Sciences.
20 (2): 130–141.

El comportamiento caótico se manifiesta en numerosos sistemas naturales, tales como el flujo de fluidos, las variaciones en los latidos del corazón y las fluctuaciones climáticas. Además, este comportamiento surge de manera espontánea en sistemas con componentes artificiales, como la bolsa de valores y el tráfico vehicular.

Este comportamiento puede ser analizado mediante un modelo matemático caótico o a través de técnicas analíticas, como los diagramas de recurrencia y los mapas de Poincaré.

La teoría del caos es fundamental en diversas disciplinas. Entre ellas se encuentran la meteorología, antropología, sociología, ciencias ambientales, informática, ingeniería, economía, ecología y la gestión de crisis pandémicas. Además, esta teoría ha sido la piedra angular para el desarrollo de campos como los sistemas dinámicos complejos, la teoría del borde del caos y los procesos de autoensamblaje.

Introducción

La teoría del caos se refiere a sistemas deterministas que, aunque pueden predecirse en principio, eventualmente muestran comportamientos que 'parecen' aleatorios.

Imagina que intentas predecir el clima. Al principio, sientes que puedes adivinar cómo será, pero después de unos días, se vuelve muy difícil y parece aleatorio. Eso es lo que dice la teoría del caos: hay cosas que podemos predecir por un corto tiempo, pero luego se vuelven impredecibles.

Esto sucede porque incluso un pequeño error en nuestra predicción o medida inicial puede hacer que nuestras predicciones futuras estén completamente desviadas. Es como intentar adivinar qué camino tomará una hoja que cae de un árbol; al principio, tal vez puedas adivinar, pero después de un rato, puede ir en cualquier dirección.

La predictibilidad de estos sistemas caóticos es temporal y su duración depende de:

La tolerancia a la incertidumbre en el pronóstico.
La precisión con la que se puede medir el estado actual del sistema.
Una escala de tiempo específica relacionada con la dinámica del sistema, conocida como tiempo de Lyapunov.

Por ejemplo, el tiempo de Lyapunov para circuitos eléctricos caóticos es de alrededor de 1 milisegundo, mientras que para sistemas meteorológicos es de algunos días (aunque esto no está probado). El sistema solar interior tiene un tiempo de Lyapunov de 4 a 5 millones de años.

En sistemas caóticos, la incertidumbre de un pronóstico crece exponencialmente con el tiempo. Matemáticamente, duplicar el tiempo de pronóstico más que duplica la incertidumbre proporcional en dicho pronóstico. Esto implica que, en términos prácticos, no es posible realizar predicciones significativas en un intervalo que exceda dos o tres veces el tiempo de Lyapunov. Cuando las predicciones ya no son significativas, el sistema se percibe como aleatorio.

Así, la Teoría del caos es un enfoque metodológico, que combina el análisis cualitativo y el cuantitativo. Su objetivo es estudiar el comportamiento de sistemas dinámicos. Estos sistemas no se entienden simplemente observando relaciones de datos individuales. En cambio, requieren un análisis basado en relaciones de datos completas y continuas.

En resumen:

La Teoría del caos es el estudio de sistemas que parecen desordenados pero que siguen patrones no visibles.
Esta teoría sostiene que pequeñas variaciones en las condiciones iniciales pueden producir cambios drásticamente diferentes en los resultados, conocido como el "efecto mariposa".
A pesar de su aparente aleatoriedad, estos sistemas pueden tener un orden subyacente y son determinados por ecuaciones matemáticas.

Dinámica caótica

Simulación geométrica del trayecto realizado por un atractor de Lorenz — Simulación geométrica, atractor de Lorenz
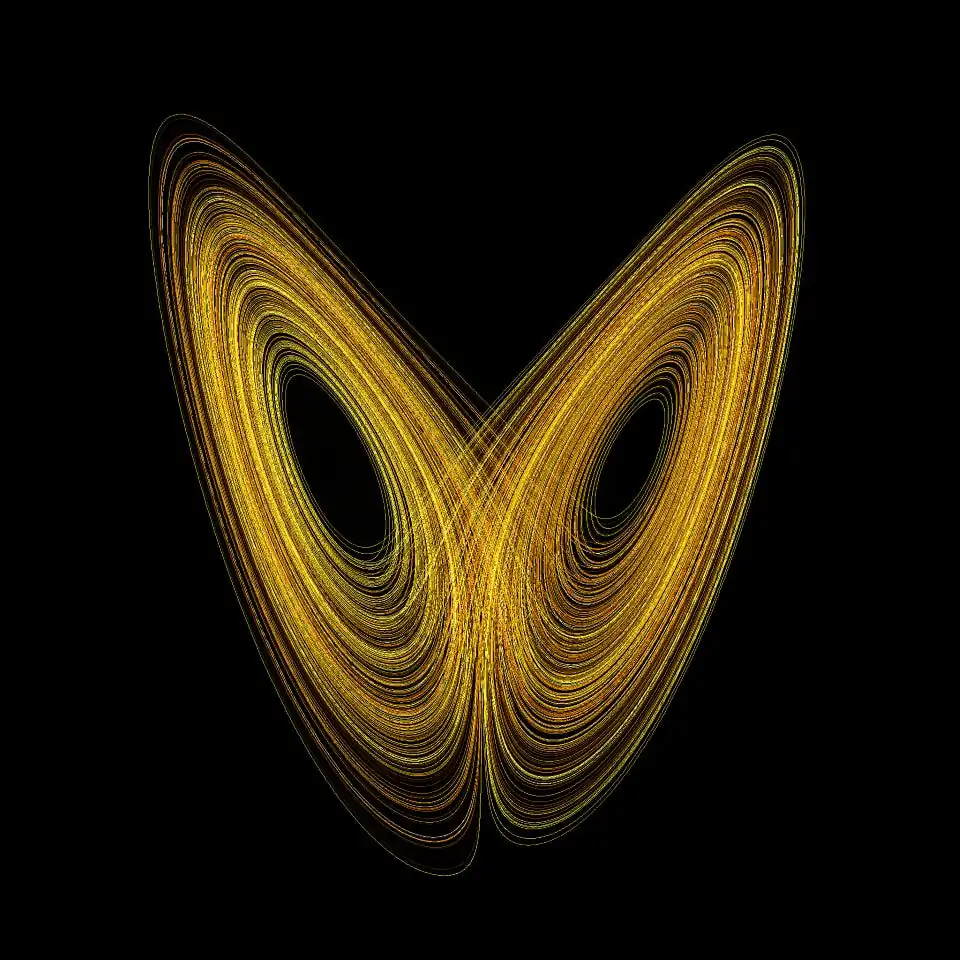
con valores r = 28, σ = 10, b = 8/3

En el lenguaje cotidiano, "caos" se refiere a "un estado de desorden". No obstante, en la teoría del caos, este término tiene una definición más precisa. Aunque no hay una definición matemática universal para el caos, una definición ampliamente reconocida, propuesta por Robert L. Devaney, establece que un sistema dinámico es caótico si cumple con las siguientes propiedades:

Debe ser sensible a las condiciones iniciales.
Debe ser topológicamente transitivo.
Debe tener órbitas periódicas densas.

Se ha comprobado que, en ciertos casos, las dos últimas propiedades implican la primera. Específicamente, para sistemas de tiempo discreto, esto es válido para todos los mapas continuos en espacios métricos. Por lo tanto, en tales situaciones, no es esencial incluir la "sensibilidad a las condiciones iniciales" en la definición, aunque suele ser la característica más destacada en aplicaciones prácticas.

Cuando nos enfocamos solo en intervalos, la segunda propiedad conlleva las otras dos. Existe una definición alternativa de caos, generalmente más laxa, que considera solo las dos primeras propiedades mencionadas.

Sensibilidad a las condiciones iniciales

HSD

La sensibilidad a las condiciones iniciales significa que cada punto en un sistema caótico se aproxima arbitrariamente a otros puntos que tienen caminos o trayectorias futuras significativamente diferentes. Por lo tanto, un cambio o perturbación arbitrariamente pequeño de la trayectoria actual puede conducir a un comportamiento futuro significativamente diferente.

La sensibilidad a las condiciones iniciales se conoce popularmente como el "efecto mariposa", llamado así por el título de un artículo presentado por Edward Lorenz en 1972 a la Asociación Estadounidense para el Avance de la Ciencia en Washington, DC, titulado Predictability: Does the Flap de las alas de una mariposa en Brasil provocó un tornado en Texas? . El aleteo representa un pequeño cambio en la condición inicial del sistema, lo que provoca una cadena de eventos que impide la previsibilidad de los fenómenos a gran escala. Si la mariposa no hubiera batido sus alas, la trayectoria del sistema general podría haber sido muy diferente.

Una consecuencia de la sensibilidad a las condiciones iniciales es que si comenzamos con una cantidad limitada de información sobre el sistema (como suele ser el caso en la práctica), más allá de cierto tiempo, el sistema ya no sería predecible. Esto es más frecuente en el caso del clima, que generalmente es predecible solo con una semana de anticipación. Esto no significa que uno no pueda afirmar nada acerca de eventos en el futuro lejano, solo que existen algunas restricciones en el sistema. Por ejemplo, sabemos que la temperatura de la superficie de la tierra no alcanzará naturalmente los 100 °C (212 °F) ni caerá por debajo de −130 °C (−202 °F) en la Tierra (durante la era geológica actual), pero no podemos predecir exactamente qué día tendrá la temperatura más alta del año.

En términos más matemáticos, el exponente de Lyapunov mide la sensibilidad a las condiciones iniciales, en forma de tasa de divergencia exponencial de las condiciones iniciales perturbadas. Más específicamente, dadas dos trayectorias iniciales en el espacio de fases que son infinitesimalmente cercanas, con separación inicial $delta mathbf {Z} _{0}$ , las dos trayectorias terminan divergiendo a una velocidad dada por ${displaystyle |delta mathbf {Z} (t)|approx e^{lambda t}|delta mathbf {Z} _{0}|,}$

donde $t$ es el tiempo y $lambda$ es el exponente de Lyapunov. La tasa de separación depende de la orientación del vector de separación inicial, por lo que puede existir un espectro completo de exponentes de Lyapunov. El número de exponentes de Lyapunov es igual al número de dimensiones del espacio de fase, aunque es común referirse solo al más grande. Por ejemplo, el exponente máximo de Lyapunov (MLE) se usa con mayor frecuencia porque determina la previsibilidad general del sistema. Un MLE positivo generalmente se toma como una indicación de que el sistema es caótico.

Además de la propiedad anterior, también existen otras propiedades relacionadas con la sensibilidad de las condiciones iniciales. Estos incluyen, por ejemplo, la mezcla teórica de medida (como se analiza en la teoría ergódica) y las propiedades de un sistema K.

No periodicidad

Un sistema caótico puede tener secuencias de valores para la variable en evolución que se repiten exactamente, dando un comportamiento periódico a partir de cualquier punto de esa secuencia. Sin embargo, tales secuencias periódicas se repelen en lugar de atraerse, lo que significa que si la variable en evolución está fuera de la secuencia, por más cercana que sea, no entrará en la secuencia y, de hecho, divergirá de ella. Así, para casi todas las condiciones iniciales, la variable evoluciona caóticamente con un comportamiento no periódico.

Mezcla topológica

La mezcla topológica (o la condición más débil de la transitividad topológica) significa que el sistema evoluciona con el tiempo de modo que cualquier región dada o conjunto abierto de su espacio de fase eventualmente se superpone con cualquier otra región dada. Este concepto matemático de "mezcla" corresponde a la intuición estándar, y la mezcla de tintes o fluidos coloreados es un ejemplo de un sistema caótico.

La mezcla topológica a menudo se omite en las descripciones populares del caos, que equiparan el caos solo con la sensibilidad a las condiciones iniciales. Sin embargo, la dependencia sensible de las condiciones iniciales por sí sola no genera caos. Por ejemplo, considere el sistema dinámico simple producido al duplicar repetidamente un valor inicial. Este sistema tiene una dependencia sensible de las condiciones iniciales en todas partes, ya que cualquier par de puntos cercanos eventualmente se separa ampliamente. Sin embargo, este ejemplo no tiene mezcla topológica y, por lo tanto, no tiene caos. De hecho, tiene un comportamiento extremadamente simple: todos los puntos excepto el 0 tienden a infinito positivo o negativo.

Transitividad topológica

Se ${ estilo de visualización f: X a X}$ dice que una aplicación es topológicamente transitiva si para cualquier par de conjuntos abiertos no vacíos ${ estilo de visualización U, V subconjunto X}$ existe 0">tal que ${displaystyle f^{k}(U)cap Vneqemptyset}$ . La transitividad topológica es una versión más débil de la mezcla topológica. Intuitivamente, si un mapa es topológicamente transitivo, dado un punto x y una región V, existe un punto y cerca de x cuya órbita pasa por V. Esto implica que es imposible descomponer el sistema en dos conjuntos abiertos.

Un teorema relacionado importante es el teorema de transitividad de Birkhoff. Es fácil ver que la existencia de una órbita densa implica transitividad topológica. El teorema de transitividad de Birkhoff establece que si X es un segundo espacio métrico completo contable, entonces la transitividad topológica implica la existencia de un conjunto denso de puntos en X que tienen órbitas densas.

Densidad de órbitas periódicas

Para que un sistema caótico tenga órbitas periódicas densas, significa que cada punto en el espacio se acerca arbitrariamente mediante órbitas periódicas. El mapa logístico unidimensional definido por x → 4 x (1 – x) es uno de los sistemas más simples con densidad de órbitas periódicas. Por ejemplo, ${tfrac {5-{sqrt {5}}}{8}}$ → ${tfrac {5+{sqrt {5}}}{8}}$ → ${tfrac {5-{sqrt {5}}}{8}}$ (o aproximadamente 0,3454915 → 0,9045085 → 0,3454915) es una órbita (inestable) de período 2, y existen órbitas similares para los períodos 4, 8, 16, etc. (de hecho, para todos los períodos especificados por el teorema de Sharkovskii).

El teorema de Sharkovskii es la base de la prueba de Li y Yorke (1975) de que cualquier sistema unidimensional continuo que muestre un ciclo regular de período tres también mostrará ciclos regulares de cualquier otra longitud, así como órbitas completamente caóticas.

Atractores extraños

Algunos sistemas dinámicos, como el mapa logístico unidimensional definido por x → 4 x (1 – x), son caóticos en todas partes, pero en muchos casos el comportamiento caótico se encuentra solo en un subconjunto del espacio de fases. Los casos de mayor interés surgen cuando el comportamiento caótico tiene lugar sobre un atractor, ya que entonces un gran conjunto de condiciones iniciales conducen a órbitas que convergen a esta región caótica.

Una manera fácil de visualizar un atractor caótico es comenzar con un punto en la cuenca de atracción del atractor y luego simplemente trazar su órbita posterior. Debido a la condición de transitividad topológica, es probable que esto produzca una imagen del atractor final completo y, de hecho, ambas órbitas que se muestran en la figura de la derecha dan una imagen de la forma general del atractor de Lorenz. Este atractor resulta de un modelo tridimensional simple del sistema meteorológico de Lorenz. El atractor de Lorenz es quizás uno de los diagramas de sistemas caóticos más conocidos, probablemente porque no solo es uno de los primeros, sino también uno de los más complejos, y como tal da lugar a un patrón muy interesante que, con un Poca imaginación, parece las alas de una mariposa.

A diferencia de los atractores de punto fijo y los ciclos límite, los atractores que surgen de sistemas caóticos, conocidos como atractores extraños, tienen gran detalle y complejidad. Los atractores extraños ocurren tanto en sistemas dinámicos continuos (como el sistema de Lorenz) como en algunos sistemas discretos (como el mapa de Hénon). Otros sistemas dinámicos discretos tienen una estructura repelente llamada conjunto de Julia, que se forma en el límite entre cuencas de atracción de puntos fijos. Los conjuntos de Julia se pueden considerar como extraños repelentes. Tanto los atractores extraños como los conjuntos de Julia suelen tener una estructura fractal y se puede calcular la dimensión fractal para ellos.

Complejidad mínima de un sistema caótico

Los sistemas caóticos discretos, como el mapa logístico, pueden exhibir atractores extraños cualquiera que sea su dimensionalidad. La universalidad de los mapas unidimensionales con máximos parabólicos y constantes ${ estilo de visualización delta = 4,669201...}$ de Feigenbaum ${ estilo de visualización alfa = 2,502907...}$ es bien visible con el mapa propuesto como un modelo de juguete para la dinámica del láser discreto: ${displaystyle xrightarrow Gx(1-mathrm {tanh} (x))}$ donde $X$ significa amplitud de campo eléctrico, $GRAMO$ es la ganancia del láser como parámetro de bifurcación. El aumento gradual de $GRAMO$ a intervalos $[0,infty)$ cambia la dinámica de regular a caótica con cualitativamente el mismo diagrama de bifurcación que los del mapa logístico.

Por el contrario, para sistemas dinámicos continuos, el teorema de Poincaré-Bendixson muestra que un atractor extraño solo puede surgir en tres o más dimensiones. Los sistemas lineales de dimensión finita nunca son caóticos; para que un sistema dinámico muestre un comportamiento caótico, debe ser no lineal o de dimensión infinita.

El teorema de Poincaré-Bendixson establece que una ecuación diferencial bidimensional tiene un comportamiento muy regular. El atractor de Lorenz discutido a continuación es generado por un sistema de tres ecuaciones diferenciales tales como: ${begin{alineado}{frac {mathrm {d} x}{mathrm {d} t}}&=sigma y-sigma x,\{frac {mathrm {d} y}{ mathrm {d} t}}&=rho x-xz-y,\{frac {mathrm {d} z}{mathrm {d} t}}&=xy-beta z.end {alineado}}$

donde $X$ , $y$ , y $z$ constituyen el estado del sistema, $t$ es el tiempo, y $sigma$ , $rho$ , $beta$ son los parámetros del sistema. Cinco de los términos del lado derecho son lineales, mientras que dos son cuadráticos; un total de siete términos. Otro atractor caótico bien conocido es generado por las ecuaciones de Rössler, que tienen solo un término no lineal de siete. Sprott encontró un sistema tridimensional con solo cinco términos, que tenía solo un término no lineal, que exhibe caos para ciertos valores de parámetros. Zhang y Heidelmostró que, al menos para los sistemas cuadráticos disipativos y conservativos, los sistemas cuadráticos tridimensionales con solo tres o cuatro términos en el lado derecho no pueden exhibir un comportamiento caótico. La razón es, simplemente, que las soluciones de tales sistemas son asintóticas a una superficie bidimensional y, por lo tanto, las soluciones se comportan bien.

Mientras que el teorema de Poincaré-Bendixson muestra que un sistema dinámico continuo en el plano euclidiano no puede ser caótico, los sistemas continuos bidimensionales con geometría no euclidiana pueden exhibir un comportamiento caótico. Quizás sorprendentemente, el caos también puede ocurrir en sistemas lineales, siempre que sean de dimensión infinita. Se está desarrollando una teoría del caos lineal en una rama del análisis matemático conocida como análisis funcional.

Mapas de dimensiones infinitas

La generalización directa de mapas discretos acoplados se basa en la integral de convolución que media la interacción entre mapas distribuidos espacialmente: ${ estilo de visualización psi _ {n + 1} ({ vec {r}}, t) = int K ({ vec {r}} - { vec {r}} ^ {,}, t) f [ psi _ {n} ({ vec {r}} ^ {,}, t)] d { vec {r}} ^ {,}}$ ,

donde el kernel ${ estilo de visualización K ({ vec {r}} - { vec {r}} ^ {,}, t)}$ es un propagador derivado como función de Green de un sistema físico relevante, podría ser un mapa logístico similar o un mapa complejo. Como ejemplos de mapas complejos, pueden servir el conjunto de Julia o el mapa de Ikeda. Cuando se consideran problemas de propagación de ondas a distancia con longitud de onda, el kernel puede tener una forma de función de Green para la ecuación de Schrödinger:. ${displaystyle f[psi _{n}({vec {r}},t)]}$ ${ estilo de visualización psi flecha derecha G psi [1- tanh ( psi)]}$ ${ estilo de visualización f [ psi] = psi ^ {2}}$ ${ estilo de visualización psi _ {n + 1} = A + B psi _ {n} e ^ {i (| psi _ {n} | ^ {2} + C)}}$ ${ estilo de visualización L = ct}$ $lambda = 2 pi / k$ $k$

${ estilo de visualización K ({ vec {r}} - { vec {r}} ^ {,}, L) = { frac {ik exp [ikL]} {2 pi L}} exp [{ frac {ik | { vec {r}} - { vec {r}} ^ {,} | ^ {2}} {2L}}]}$ .

Sistemas de tirones

En física, jerk es la tercera derivada de posición, con respecto al tiempo. Como tal, las ecuaciones diferenciales de la forma $Jleft({overset {...}{x}},{ddot {x}},{dot {x}},xright)=0$

a veces se les llama ecuaciones de idiotas. Se ha demostrado que una ecuación jerk, que es equivalente a un sistema de tres ecuaciones diferenciales no lineales ordinarias de primer orden, es en cierto sentido el escenario mínimo para soluciones que muestran un comportamiento caótico. Esto motiva el interés matemático en los sistemas jerk. Los sistemas que involucran una derivada cuarta o superior se denominan, en consecuencia, sistemas de hipertirones.

El comportamiento de un sistema de sacudidas se describe mediante una ecuación de sacudidas, y para ciertas ecuaciones de sacudidas, los circuitos electrónicos simples pueden modelar soluciones. Estos circuitos se conocen como circuitos jerk.

Una de las propiedades más interesantes de los circuitos jerk es la posibilidad de un comportamiento caótico. De hecho, ciertos sistemas caóticos bien conocidos, como el atractor de Lorenz y el mapa de Rössler, se describen convencionalmente como un sistema de tres ecuaciones diferenciales de primer orden que se pueden combinar en una sola (aunque bastante complicada) ecuación de sacudidas. Otro ejemplo de una ecuación de tirón con no linealidad en la magnitud de $X$ es: ${frac {mathrm {d} ^{3}x}{mathrm {d} t^{3}}}+A{frac {mathrm {d} ^{2}x}{mathrm {d } t^{2}}}+{frac {mathrm {d} x}{mathrm {d} t}}-|x|+1=0.$

Aquí, A es un parámetro ajustable. Esta ecuación tiene una solución caótica para A = 3/5 y se puede implementar con el siguiente circuito jerk; la no linealidad requerida es provocada por los dos diodos:

En el circuito anterior, todas las resistencias tienen el mismo valor, excepto $R_{A}=R/A=5R/3$ , y todos los capacitores tienen el mismo tamaño. La frecuencia dominante es $1/2 pi RC$ . La salida del amplificador operacional 0 corresponderá a la variable x, la salida de 1 corresponde a la primera derivada de x y la salida de 2 corresponde a la segunda derivada.

Los circuitos similares solo requieren un diodo o ningún diodo.

Véase también el conocido circuito de Chua, una base para generadores caóticos de números aleatorios verdaderos. La facilidad de construcción del circuito lo ha convertido en un ejemplo omnipresente del mundo real de un sistema caótico.

Orden espontáneo

Bajo las condiciones adecuadas, el caos evoluciona espontáneamente en un patrón de bloqueo. En el modelo de Kuramoto, cuatro condiciones son suficientes para producir sincronización en un sistema caótico. Los ejemplos incluyen la oscilación acoplada de los péndulos, luciérnagas, neuronas de Christiaan Huygens, la resonancia del Puente del Milenio de Londres y grandes conjuntos de uniones de Josephson.

Historia

Uno de los primeros defensores de la teoría del caos fue Henri Poincaré. En la década de 1880, mientras estudiaba el problema de los tres cuerpos, descubrió que puede haber órbitas que no son periódicas y, sin embargo, no aumentan constantemente ni se aproximan a un punto fijo. En 1898, Jacques Hadamard publicó un influyente estudio sobre el movimiento caótico de una partícula libre que se desliza sin fricción sobre una superficie de curvatura negativa constante, llamado "billar de Hadamard". Hadamard pudo demostrar que todas las trayectorias son inestables, en el sentido de que todas las trayectorias de las partículas divergen exponencialmente entre sí, con un exponente de Lyapunov positivo.

La teoría del caos comenzó en el campo de la teoría ergódica. Estudios posteriores, también sobre el tema de las ecuaciones diferenciales no lineales, fueron realizados por George David Birkhoff, Andrey Nikolaevich Kolmogorov, Mary Lucy Cartwright y John Edensor Littlewood, y Stephen Smale. A excepción de Smale, todos estos estudios se inspiraron directamente en la física: el problema de los tres cuerpos en el caso de Birkhoff, la turbulencia y los problemas astronómicos en el caso de Kolmogorov, y la ingeniería de radio en el caso de Cartwright y Littlewood. Aunque no se había observado el movimiento planetario caótico, los experimentadores habían encontrado turbulencia en el movimiento de fluidos y oscilaciones no periódicas en los circuitos de radio sin el beneficio de una teoría que explicara lo que estaban viendo.

A pesar de las ideas iniciales en la primera mitad del siglo XX, la teoría del caos se formalizó como tal solo después de mediados de siglo, cuando se hizo evidente para algunos científicos que la teoría lineal, la teoría de sistemas predominante en ese momento, simplemente no podía explicar el observado. comportamiento de ciertos experimentos como el del mapa logístico. Lo que se había atribuido a la imprecisión de la medida y al simple "ruido" fue considerado por los teóricos del caos como un componente completo de los sistemas estudiados.

El principal catalizador para el desarrollo de la teoría del caos fue la computadora electrónica. Gran parte de las matemáticas de la teoría del caos implica la iteración repetida de fórmulas matemáticas simples, lo que sería poco práctico hacerlo a mano. Las computadoras electrónicas hicieron prácticos estos cálculos repetidos, mientras que las figuras y las imágenes hicieron posible visualizar estos sistemas. Como estudiante de posgrado en el laboratorio de Chihiro Hayashi en la Universidad de Kyoto, Yoshisuke Ueda estaba experimentando con computadoras analógicas y notó, el 27 de noviembre de 1961, lo que llamó "fenómenos de transición aleatoria". Sin embargo, su asesor no estuvo de acuerdo con sus conclusiones en ese momento y no le permitió informar sobre sus hallazgos hasta 1970.

Edward Lorenz fue uno de los primeros pioneros de la teoría. Su interés por el caos surgió accidentalmente a través de su trabajo sobre la predicción del tiempo en 1961.Lorenz estaba usando una computadora digital simple, una Royal McBee LGP-30, para ejecutar su simulación meteorológica. Quería volver a ver una secuencia de datos y, para ahorrar tiempo, inició la simulación en la mitad de su curso. Lo hizo ingresando una copia impresa de los datos que correspondían a las condiciones en medio de la simulación original. Para su sorpresa, el clima que la máquina comenzó a predecir era completamente diferente al cálculo anterior. Lorenz rastreó esto hasta la copia impresa de la computadora. La computadora funcionó con una precisión de 6 dígitos, pero la impresión redondeó las variables a un número de 3 dígitos, por lo que un valor como 0,506127 se imprimió como 0,506. Esta diferencia es pequeña, y el consenso en ese momento habría sido que no debería tener ningún efecto práctico. Sin embargo,El descubrimiento de Lorenz, que dio su nombre a los atractores de Lorenz, mostró que incluso los modelos atmosféricos detallados no pueden, en general, hacer predicciones meteorológicas precisas a largo plazo.

En 1963, Benoit Mandelbrot encontró patrones recurrentes en todas las escalas en los datos sobre los precios del algodón. Previamente había estudiado teoría de la información y concluyó que el ruido estaba modelado como un conjunto de Cantor: en cualquier escala, la proporción de períodos que contenían ruido y períodos libres de errores era una constante; por lo tanto, los errores eran inevitables y debían planificarse mediante la incorporación de redundancia. Mandelbrot describió tanto el "efecto Noah" (en el que pueden ocurrir cambios discontinuos repentinos) como el "efecto Joseph" (en el que la persistencia de un valor puede ocurrir durante un tiempo, y luego cambiar repentinamente).Esto desafió la idea de que los cambios en el precio se distribuyeron normalmente. En 1967, publicó "¿Cuánto mide la costa de Gran Bretaña? Autosimilitud estadística y dimensión fraccionaria", mostrando que la longitud de una costa varía con la escala del instrumento de medición, se parece a sí misma en todas las escalas y tiene una longitud infinita para un Dispositivo de medición infinitesimalmente pequeño. Argumentando que una bola de hilo aparece como un punto cuando se ve desde lejos (dimensión 0), una bola cuando se ve bastante cerca (tridimensional) o un hilo curvo (unidimensional), argumentó que las dimensiones de un objeto son relativas al observador y pueden ser fraccionarias. Un objeto cuya irregularidad es constante en diferentes escalas ("autosimilitud") es un fractal (los ejemplos incluyen la esponja de Menger, la junta de Sierpiński,copo de nieve, que es infinitamente largo pero encierra un espacio finito y tiene una dimensión fractal de alrededor de 1.2619). En 1982, Mandelbrot publicó La geometría fractal de la naturaleza, que se convirtió en un clásico de la teoría del caos.

En diciembre de 1977, la Academia de Ciencias de Nueva York organizó el primer simposio sobre el caos, al que asistieron David Ruelle, Robert May, James A. Yorke (autor del término "caos" en las matemáticas), Robert Shaw y el meteorólogo Edward Lorenz. Al año siguiente, Pierre Coullet y Charles Tresser publicaron "Itérations d'endomorphismes et groupe de renormalisation", y el artículo de Mitchell Feigenbaum "Quantitative Universality for a Class of Nonlinear Transformations" finalmente apareció en una revista, después de 3 años de rechazos de árbitros. Así Feigenbaum (1975) y Coullet & Tresser (1978) descubrieron la universalidad del caos, permitiendo la aplicación de la teoría del caos a muchos fenómenos diferentes.

En 1979, Albert J. Libchaber, durante un simposio organizado en Aspen por Pierre Hohenberg, presentó su observación experimental de la cascada de bifurcación que conduce al caos y la turbulencia en los sistemas de convección Rayleigh-Bénard. Fue galardonado con el Premio Wolf de Física en 1986 junto con Mitchell J. Feigenbaum por sus logros inspiradores.

En 1986, la Academia de Ciencias de Nueva York coorganizó con el Instituto Nacional de Salud Mental y la Oficina de Investigación Naval la primera conferencia importante sobre el caos en biología y medicina. Allí, Bernardo Huberman presentó un modelo matemático de la disfunción del seguimiento ocular entre los esquizofrénicos. Esto condujo a una renovación de la fisiología en la década de 1980 mediante la aplicación de la teoría del caos, por ejemplo, en el estudio de los ciclos cardíacos patológicos.

En 1987, Per Bak, Chao Tang y Kurt Wiesenfeld publicaron un artículo en Physical Review Letters en el que describían por primera vez la criticidad autoorganizada (SOC), considerada uno de los mecanismos por los que surge la complejidad en la naturaleza.

HSD

Junto con los enfoques mayormente basados en laboratorio, como la pila de arena de Bak-Tang-Wiesenfeld, se han realizado numerosas investigaciones en sistemas sociales o naturales a gran escala. Se cree que estos sistemas muestran un comportamiento invariable en escala. A pesar de que estos enfoques no siempre fueron bien recibidos por los expertos en los campos estudiados, la SOC (Self-Organized Criticality) se ha consolidado como una teoría clave para explicar diversos fenómenos naturales.

Entre estos fenómenos se encuentran los terremotos, que ya eran conocidos por su comportamiento de escala invariable mucho antes de descubrirse la SOC. Ejemplos de esto son la ley de Gutenberg-Richter, que describe la distribución estadística de los tamaños de los terremotos, y la ley de Omori, que aborda la frecuencia de las réplicas. Otros fenómenos que se han estudiado bajo la lente de la SOC incluyen erupciones solares, fluctuaciones en sistemas económicos como los mercados financieros (donde las referencias a SOC son comunes en econofísica), formación del paisaje, incendios forestales, deslizamientos de tierra, epidemias y evolución biológica. En este último, la SOC ha sido propuesta como el mecanismo dinámico detrás de la teoría de los "equilibrios puntuados" de Niles Eldredge y Stephen Jay Gould.

Dada la relevancia de una distribución libre de escala en el tamaño de los eventos, algunos investigadores sugieren que las guerras también deberían ser consideradas como un ejemplo de SOC. Las investigaciones en este campo han abordado tanto el modelado, desarrollando o adaptando modelos existentes a sistemas naturales específicos, como el análisis exhaustivo de datos para determinar la existencia y características de las leyes de escala naturales.

HSD

En el mismo año, James Gleick publicó Chaos: Making a New Science, que se convirtió en un éxito de ventas y presentó los principios generales de la teoría del caos, así como su historia al público en general. Inicialmente dominio de unos pocos individuos aislados, la teoría del caos emergió progresivamente como una disciplina transdisciplinaria e institucional, principalmente bajo el nombre de análisis de sistemas no lineales. Aludiendo al concepto de cambio de paradigma de Thomas Kuhn expuesto en La estructura de las revoluciones científicas (1962), muchos "caólogos" (como algunos se describieron a sí mismos) afirmaron que esta nueva teoría era un ejemplo de tal cambio, una tesis defendida por Gleick.

La disponibilidad de computadoras más baratas y potentes amplía la aplicabilidad de la teoría del caos. Actualmente, la teoría del caos sigue siendo un área activa de investigación, que involucra muchas disciplinas diferentes, como matemáticas, topología, física, sistemas sociales, modelado de poblaciones, biología, meteorología, astrofísica, teoría de la información, neurociencia computacional, gestión de crisis pandémicas, etc.

Aplicaciones

Modelo de tráfico Biham–Middleton–Levine (BML)

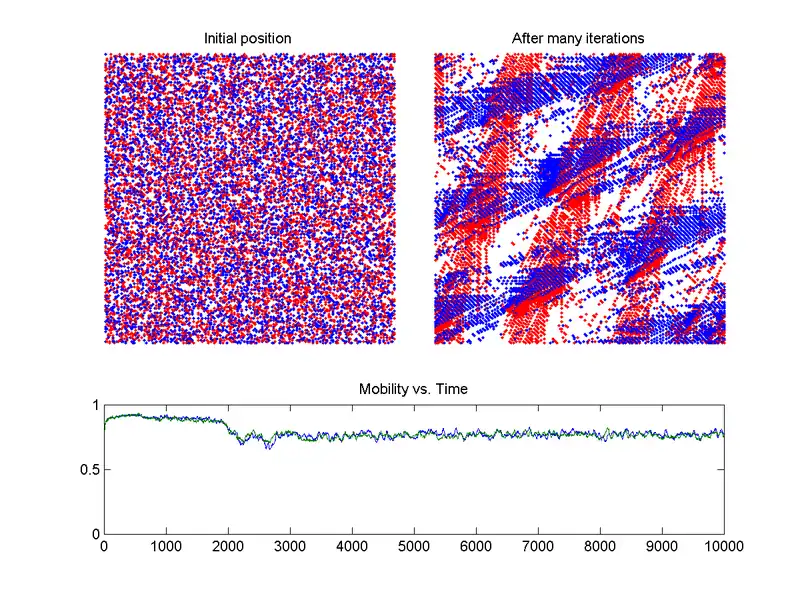
Aunque la teoría del caos nació de la observación de patrones climáticos, se ha vuelto aplicable a una variedad de otras situaciones. Algunas áreas que se benefician de la teoría del caos en la actualidad son la geología, las matemáticas, la biología, la informática, la economía, la ingeniería, las finanzas, la meteorología, la filosofía, la antropología, la física, la política, la dinámica demográfica y la robótica. A continuación se enumeran algunas categorías con ejemplos, pero de ninguna manera se trata de una lista completa, ya que están apareciendo nuevas aplicaciones.

Criptografía

La teoría del caos se ha utilizado durante muchos años en criptografía. En las últimas décadas, el caos y la dinámica no lineal se han utilizado en el diseño de cientos de primitivas criptográficas. Estos algoritmos incluyen algoritmos de cifrado de imágenes, funciones hash, generadores de números pseudoaleatorios seguros, cifrados de flujo, marcas de agua y esteganografía. La mayoría de estos algoritmos se basan en mapas caóticos unimodales y una gran parte de estos algoritmos utilizan los parámetros de control y la condición inicial de los mapas caóticos como sus claves. Desde una perspectiva más amplia, sin pérdida de generalidad, las similitudes entre los mapas caóticos y los sistemas criptográficos es la principal motivación para el diseño de algoritmos criptográficos basados en el caos.Un tipo de encriptación, clave secreta o clave simétrica, se basa en la difusión y la confusión, que está bien modelada por la teoría del caos. Otro tipo de computación, la computación de ADN, cuando se combina con la teoría del caos, ofrece una forma de cifrar imágenes y otra información. Se ha demostrado que muchos de los algoritmos criptográficos de DNA-Chaos no son seguros o se sugiere que la técnica aplicada no es eficiente.

Robótica

La robótica es otra área que recientemente se ha beneficiado de la teoría del caos. En lugar de que los robots actúen en un tipo de refinamiento de prueba y error para interactuar con su entorno, se ha utilizado la teoría del caos para construir un modelo predictivo. La dinámica caótica ha sido exhibida por robots bípedos pasivos que caminan.

Biología

Durante más de cien años, los biólogos han realizado un seguimiento de las poblaciones de diferentes especies con modelos de población. La mayoría de los modelos son continuos, pero recientemente los científicos han podido implementar modelos caóticos en ciertas poblaciones. Por ejemplo, un estudio sobre modelos de lince canadiense mostró que hubo un comportamiento caótico en el crecimiento de la población. El caos también se puede encontrar en los sistemas ecológicos, como la hidrología. Si bien un modelo caótico para la hidrología tiene sus defectos, todavía hay mucho que aprender al observar los datos a través de la lente de la teoría del caos.Otra aplicación biológica se encuentra en la cardiotocografía. La vigilancia fetal es un delicado equilibrio entre obtener información precisa y ser lo menos invasiva posible. Se pueden obtener mejores modelos de signos de advertencia de hipoxia fetal a través del modelado caótico.

Ciencias económicas

Es posible que los modelos económicos también puedan mejorarse mediante la aplicación de la teoría del caos, pero predecir la salud de un sistema económico y qué factores lo influyen más es una tarea extremadamente compleja. Los sistemas económicos y financieros son fundamentalmente diferentes de los de las ciencias naturales clásicas, ya que los primeros son inherentemente de naturaleza estocástica, ya que resultan de las interacciones de las personas y, por lo tanto, es poco probable que los modelos deterministas puros proporcionen representaciones precisas de los datos. La literatura empírica que prueba el caos en economía y finanzas presenta resultados muy variados, en parte debido a la confusión entre pruebas específicas para el caos y pruebas más generales para relaciones no lineales.

El caos se puede encontrar en la economía por medio del análisis de cuantificación de recurrencia. De hecho, Orlando et al. por medio del llamado índice de correlación de cuantificación de recurrencia fueron capaces de detectar cambios ocultos en las series temporales. Luego, se empleó la misma técnica para detectar transiciones de fases laminares (regulares) a turbulentas (caóticas), así como diferencias entre variables macroeconómicas y resaltar características ocultas de la dinámica económica. Finalmente, el caos podría ayudar a modelar el funcionamiento de la economía, así como a incorporar impactos debido a eventos externos como el COVID-19. Para una descripción actualizada de las herramientas y los resultados obtenidos al calibrar y probar empíricamente modelos caóticos deterministas (p. ej., Kaldor-Kalecki, Goodwin, Harrod), see Orlando et al.

Otras areas

En química, la predicción de la solubilidad de los gases es esencial para la fabricación de polímeros, pero los modelos que utilizan la optimización de enjambre de partículas (PSO) tienden a converger en los puntos equivocados. Se ha creado una versión mejorada de PSO mediante la introducción del caos, lo que evita que las simulaciones se atasquen. En mecánica celeste, especialmente cuando se observan asteroides, la aplicación de la teoría del caos conduce a mejores predicciones sobre cuándo estos objetos se acercarán a la Tierra y a otros planetas. Cuatro de las cinco lunas de Plutón giran caóticamente. En física cuántica e ingeniería eléctrica, el estudio de grandes conjuntos de uniones de Josephson se benefició enormemente de la teoría del caos.Más cerca de casa, las minas de carbón siempre han sido lugares peligrosos donde las frecuentes fugas de gas natural causan muchas muertes. Hasta hace poco, no había una forma fiable de predecir cuándo ocurrirían. Pero estas fugas de gas tienen tendencias caóticas que, cuando se modelan adecuadamente, se pueden predecir con bastante precisión.

La teoría del caos se puede aplicar fuera de las ciencias naturales, pero históricamente casi todos estos estudios han sufrido de falta de reproducibilidad; poca validez externa; y/o falta de atención a la validación cruzada, lo que resulta en una precisión predictiva deficiente (si incluso se ha intentado una predicción fuera de la muestra). Glass, Mandell y Selz han descubierto que ningún estudio de EEG ha indicado hasta ahora la presencia de atractores extraños u otros signos de comportamiento caótico.

Los investigadores han seguido aplicando la teoría del caos a la psicología. Por ejemplo, al modelar el comportamiento de un grupo en el que los miembros heterogéneos pueden comportarse como si compartieran en diferentes grados lo que en la teoría de Wilfred Bion es un supuesto básico, los investigadores han encontrado que la dinámica del grupo es el resultado de la dinámica individual de los miembros: cada individuo reproduce la dinámica del grupo en una escala diferente, y el comportamiento caótico del grupo se refleja en cada miembro.

Redington y Reidbord (1992) intentaron demostrar que el corazón humano podía mostrar rasgos caóticos. Supervisaron los cambios en los intervalos entre latidos del corazón de una sola paciente de psicoterapia a medida que avanzaba a través de períodos de intensidad emocional variable durante una sesión de terapia. Se admite que los resultados no fueron concluyentes. No solo hubo ambigüedades en los diversos gráficos que produjeron los autores para supuestamente mostrar evidencia de dinámica caótica (análisis espectral, trayectoria de fase y gráficos de autocorrelación), sino también cuando intentaron calcular un exponente de Lyapunov como una confirmación más definitiva del comportamiento caótico, el los autores encontraron que no podían hacerlo de manera confiable.

En su artículo de 1995, Metcalf y Allen sostuvieron que descubrieron en el comportamiento animal un patrón de duplicación del período que conduce al caos. Los autores examinaron una respuesta bien conocida llamada polidipsia inducida por el horario, por la cual un animal privado de comida durante cierto tiempo beberá cantidades inusuales de agua cuando finalmente se le presente la comida. El parámetro de control (r) que operaba aquí era la duración del intervalo entre tomas, una vez reanudadas. Los autores tuvieron cuidado de probar una gran cantidad de animales e incluir muchas repeticiones, y diseñaron su experimento para descartar la probabilidad de que los cambios en los patrones de respuesta fueran causados por diferentes puntos de partida para r.

Las series de tiempo y los diagramas de primer retraso brindan el mejor respaldo para las afirmaciones realizadas, mostrando una marcha bastante clara de la periodicidad a la irregularidad a medida que se incrementan los tiempos de alimentación. Los diversos gráficos de trayectoria de fase y análisis espectrales, por otro lado, no coinciden lo suficientemente bien con los otros gráficos o con la teoría general como para conducir inexorablemente a un diagnóstico caótico. Por ejemplo, las trayectorias de las fases no muestran una progresión definida hacia una complejidad cada vez mayor (y alejándose de la periodicidad); el proceso parece bastante confuso. Además, donde Metcalf y Allen vieron períodos de dos y seis en sus diagramas espectrales, hay espacio para interpretaciones alternativas. Toda esta ambigüedad requiere una explicación serpenteante y post-hoc para mostrar que los resultados se ajustan a un modelo caótico.

Al adaptar un modelo de asesoramiento profesional para incluir una interpretación caótica de la relación entre los empleados y el mercado laboral, Amundson y Bright descubrieron que se pueden hacer mejores sugerencias a las personas que luchan con las decisiones profesionales. Las organizaciones modernas se ven cada vez más como sistemas adaptativos complejos abiertos con estructuras no lineales naturales fundamentales, sujetas a fuerzas internas y externas que pueden contribuir al caos. Por ejemplo, la creación de equipos y el desarrollo de grupos se están investigando cada vez más como un sistema inherentemente impredecible, ya que la incertidumbre de diferentes personas que se encuentran por primera vez hace que la trayectoria del equipo sea incognoscible.

Algunos dicen que la metáfora del caos, utilizada en teorías verbales, basada en modelos matemáticos y aspectos psicológicos del comportamiento humano, brinda información útil para describir la complejidad de los pequeños grupos de trabajo, que van más allá de la metáfora misma.

La previsión del tráfico puede beneficiarse de las aplicaciones de la teoría del caos. Mejores predicciones de cuándo ocurrirá el tráfico permitirían tomar medidas para dispersarlo antes de que haya ocurrido. La combinación de los principios de la teoría del caos con algunos otros métodos ha llevado a un modelo de predicción a corto plazo más preciso (consulte el gráfico del modelo de tráfico BML a la derecha).

La teoría del caos se ha aplicado a los datos ambientales del ciclo del agua (también datos hidrológicos), como la lluvia y el caudal. Estos estudios han arrojado resultados controvertidos, porque los métodos para detectar una firma caótica suelen ser relativamente subjetivos. Los primeros estudios tendían a "tener éxito" en encontrar el caos, mientras que los estudios y metanálisis posteriores cuestionaron esos estudios y proporcionaron explicaciones de por qué es probable que estos conjuntos de datos no tengan una dinámica caótica de baja dimensión.

Contenido relacionado

Más resultados...